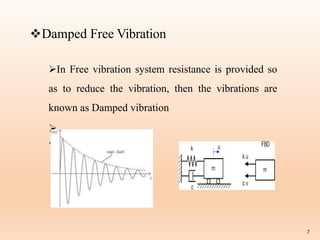
1. Vibration is defined as the periodic oscillation of a body or system about an equilibrium point due to elastic forces. There are two types of vibration: free vibration and forced vibration. 2. Free vibration occurs when a system vibrates on its own after an initial displacement, without any external forces. The system oscillates at its natural frequency. Forced vibration occurs when a periodic external force causes the system to vibrate at the frequency of the applied force. 3. D'Alembert's principle states that the inertia force on an oscillating body is equal and opposite to its acceleration. Applying this principle, the natural frequency of a spring-mass system can be derived as the square root of

1. 1
Vibration
•Mechanical vibration is defined as the measurement
of a periodic process of oscillations with respect to an
equilibrium point.
•Such cyclic motion of a body or a system, due to
elastic deformation under the action of external forces,
is known as vibration.

2. 2
Free Vibration
If the external forces is remove after giving an initially
displacement to the system, then the system vibrates on its
own due to internal elastic forces. Such as that type
vibration know as free vibration.
Examples of free vibrations is oscillations of a pendulum
about a vertical equilibrium position.

3. The frequency of free vibration is known as free or
natural frequency (f n ).
2
, Hz
3
f 
n
n
Characteristics:
the system oscillates with constant frequency and amplitude
the system oscillates with its natural frequency
the total energy of the oscillator remains constant

4. 4
Forced Vibration
If system or a body is subjected to a periodic external
force, then the resulting vibration are known as forced
vibration.
When an external force is acting, the body does not vibrate
with its own natural frequency, but vibrates with the
frequency of the applied external force.

5. 5
 Examples of forced vibrations are, vibrations of I.C. Engines,
electric motor, centrifugal pump.
 Cause Of Forced Vibration In Rotating Mass:
Electric motor, turbine, other rotating machineries have some
amount of unbalance left in them even after rectifying their unbalance
on precision balancing machines. This unbalanced rotating mass
produces centrifugal force which acts as exciting force and causes
forced vibrations of the machine.

6. Undamped Free Vibration
In Free vibration there is on external artificial
resistance to the vibration then such vibration are
known as Undamped Free Vibration .
6

7. Damped Free Vibration
In Free vibration system resistance is provided so
as to reduce the vibration, then the vibrations are
known as Damped vibration

.
7

8. D'Alembert's Principal :-
 This inertia force is equal to the mass times the
acceleration and its direction is opposite to that acceleration.
Consider a spring-mass system constrained to move along the axis
of the spring, as shown in fig.
Where m = mass suspended from the spring end ,kg.
K = stiffness of spring N/m.
 = defilation of the spring due to weight mg, m.
x = displacement given to the mass, by application of
initial external force, from mean position, m.
8

9. 
k
m m
x
W=mg
Fig.1 Equilibrium method
9
 The forces acting on the mas
.s
. are:
1. Inertia force , m x (upward)
2. Spring force or restoring force, Kx  
3. Gravitational force, mg (downward)
(downward)

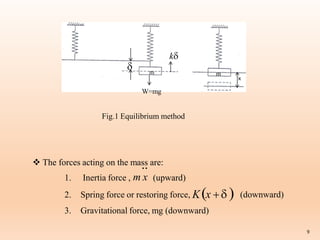
10.  According to D'Alembert's Principal,
..
Inertiaforce Externalforce 0
m x kx   mg  0
[Taking upward forces as +ve and downward force as -ve]
..
10
x  0
K
m
x
m x Kx  K  mg  0
..
mg  K From fig.
 We know that, the fundamental equation of SHM is,
n
..
x  
2
x  0 …….2
……..1

11. Comparing equation 1&2
m
K
n 
2
 n
 
K
,rad /sec
m
or
Where, ωn  circularnaturalfrequency,rad/s
The natural frequency ‘fn’of vibration is,
2

n
fn
or K
, Hz
2 m
11

1
fn
Also, from fig.
mg  K  m 

K

g
…….3
…….4

12. Substituting Equation (4) in equation (3) we get,
g
, Hz
2 

1
fn
 The time period ‘ tp
’ is,
1 K
2 m
1
fn
p
t 
1

or m
12
tp  2
K
,s

13. 13