Embed presentation
Downloaded 23 times



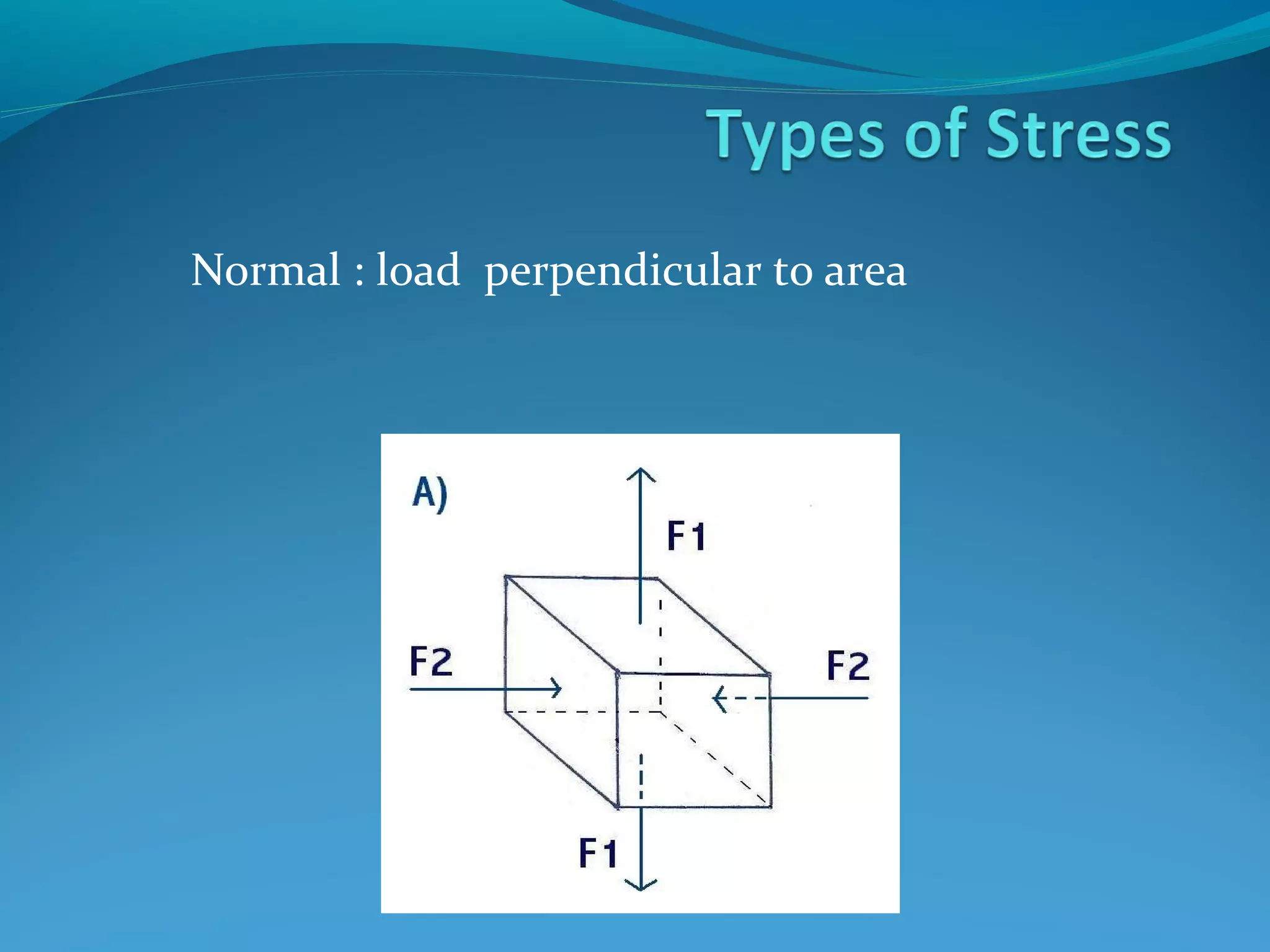











![Relating Stress and Strain
Shear
Hooke’s Law
τ = G γ
Shear Modulus
G = E / [2 (1+ ν )]
τ = shear stress
G = shear modulus
γ = shear strain](https://image.slidesharecdn.com/stressandstrain-sectionc-161124193402/75/Stress-and-strain-section-c-16-2048.jpg)







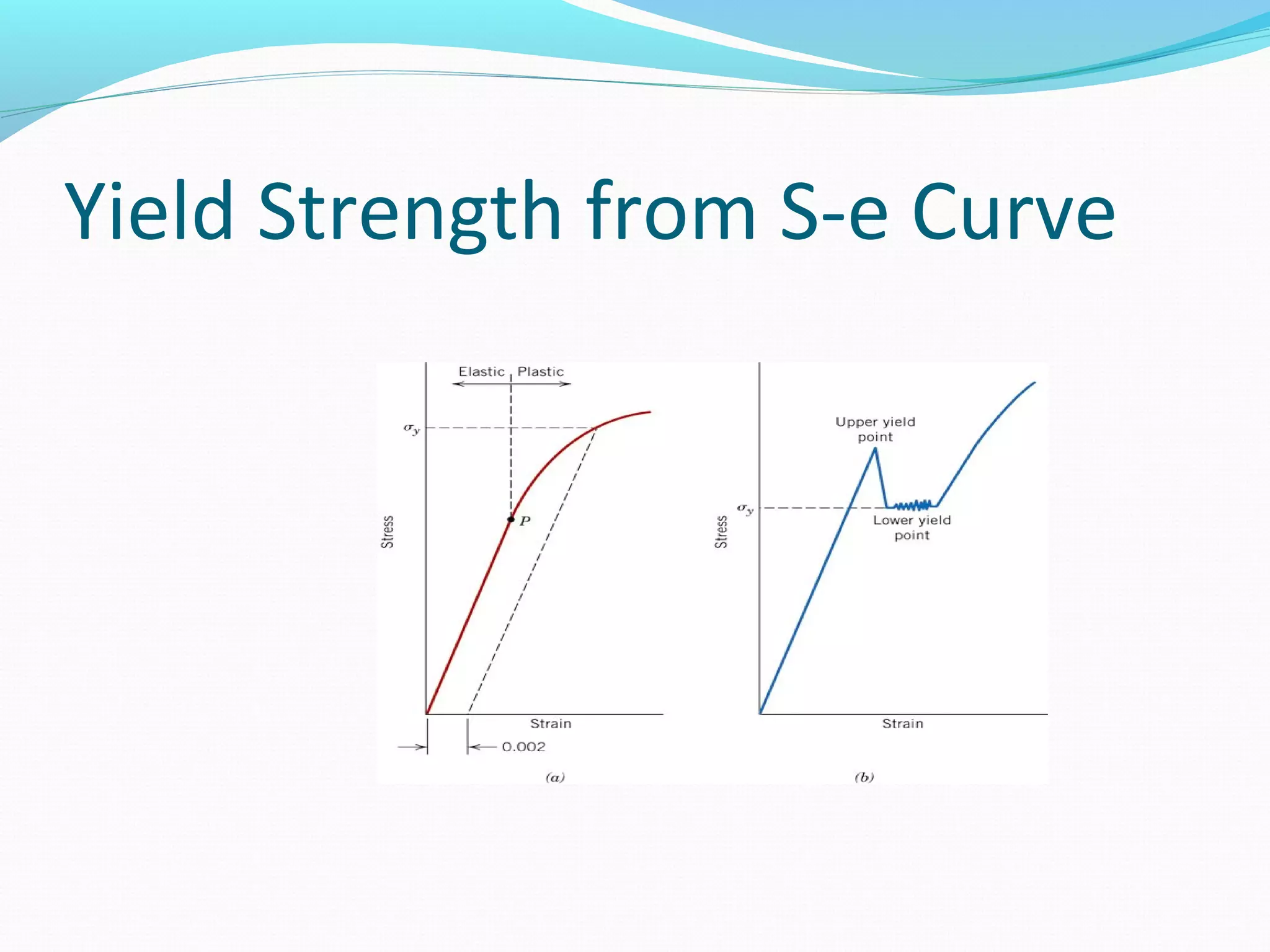


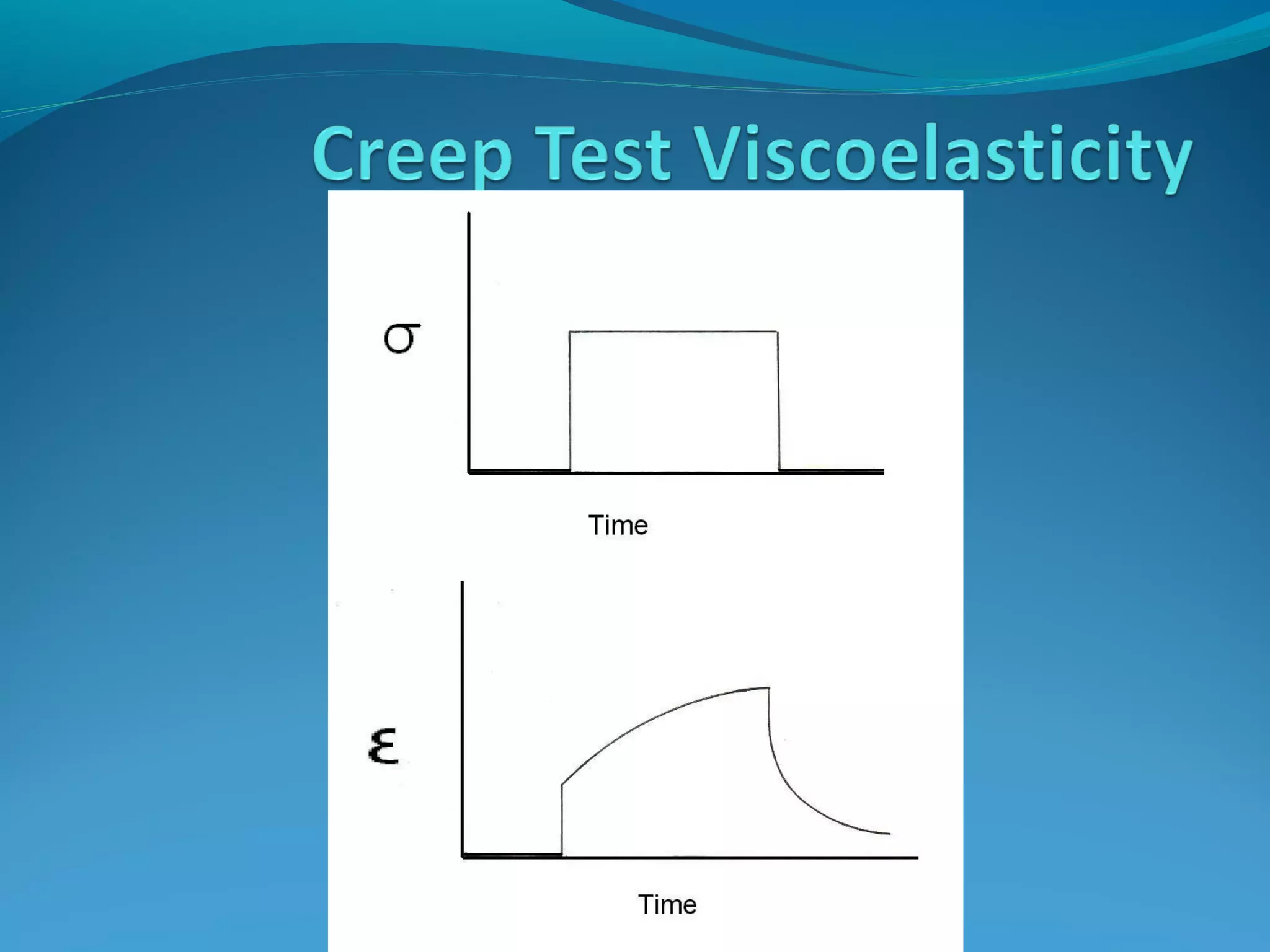


The document outlines the fundamental concepts of stress and strain, including definitions, types, and relationships such as Hooke’s law. It explains the calculation of material parameters from stress-strain curves and describes elastic and plastic deformation. Additionally, it includes specific values for Poisson's ratio and material moduli for various materials.















![Relating Stress and Strain
Shear
Hooke’s Law
τ = G γ
Shear Modulus
G = E / [2 (1+ ν )]
τ = shear stress
G = shear modulus
γ = shear strain](https://image.slidesharecdn.com/stressandstrain-sectionc-161124193402/75/Stress-and-strain-section-c-16-2048.jpg)











