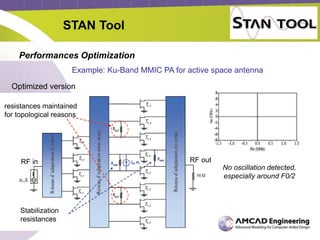
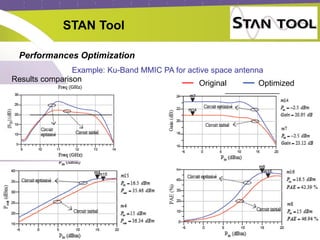
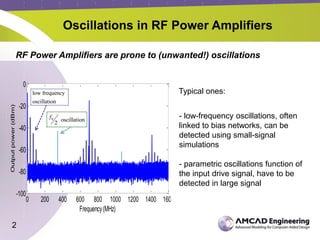
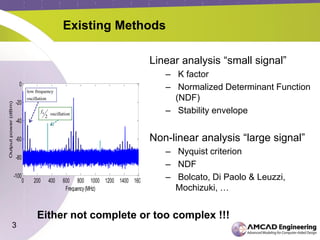
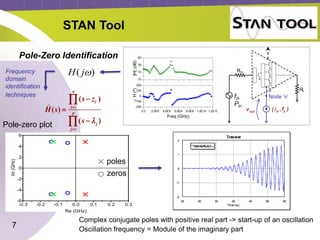
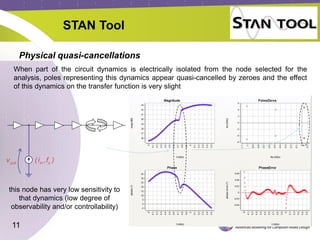
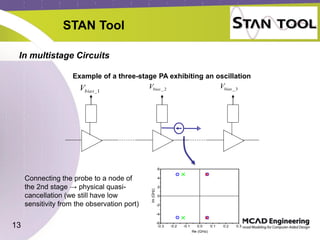
The document discusses the stability analysis of microwave circuits, particularly focusing on low-frequency oscillations in RF power amplifiers. It outlines existing methods for detecting oscillations, their limitations, and presents the STAN tool for linear and non-linear stability analysis. The tool aids in identifying oscillation modes and applying suitable stabilization strategies to improve amplifier performance.

1. 1
STAN Tool
Stability Analysis of Microwave
Circuits

2. 2
0 200 400 600 800 1000 1200 1400 1600
-100
-80
-60
-40
-20
0
Frequency(MHz)
Outputpower(dBm)
0 200 400 600 800 1000 1200 1400 1600
-100
-80
-60
-40
-20
0
Frequency(MHz)
Outputpower(dBm)
0 200 400 600 800 1000 1200 1400 1600
-100
-80
-60
-40
-20
0
Frequency(MHz)
Outputpower(dBm)
0 oscillation
2
f
low frequency
oscillation
Oscillations in RF Power Amplifiers
- low-frequency oscillations, often
linked to bias networks, can be
detected using small-signal
simulations
RF Power Amplifiers are prone to (unwanted!) oscillations
- parametric oscillations function of
the input drive signal, have to be
detected in large signal
Typical ones:

3. 3
Linear analysis “small signal”
– K factor
– Normalized Determinant Function
(NDF)
– Stability envelope
Non-linear analysis “large signal”
– Nyquist criterion
– NDF
– Bolcato, Di Paolo & Leuzzi,
Mochizuki, …
0 200 400 600 800 1000 1200 1400 1600
-100
-80
-60
-40
-20
0
Frequency(MHz)
Outputpower(dBm)
0 200 400 600 800 1000 1200 1400 1600
-100
-80
-60
-40
-20
0
Frequency(MHz)
Outputpower(dBm)
0 200 400 600 800 1000 1200 1400 1600
-100
-80
-60
-40
-20
0
Frequency(MHz)
Outputpower(dBm)
0 oscillation
2
f
low frequency
oscillation
Existing Methods
Either not complete or too complex !!!

4. 4
Existing Methods
Linear analysis
Widely used: K factor (also µ and µ’ now)
- K>1 & |∆| <1: unconditional stability of two port network
- K<1: conditional stability  stability circles
Unconditional stability Conditional stability Unconditional instability
Only indicates that a stable circuit will continue to be stable when loading it with
passive external loads at the input or output
Do not guarantee the internal stability of the circuit !
Limitations:

5. 5
Existing Methods
IN
OUT Gate Drain
Source
Multi-stage power amplifier Multi-fingers transistor
Linear analysis
Potentially instable architectures for which K factor is not
enough

6. 6
Objectives:
- Detect potential oscillations
- Get knowledge on oscillation
localization and oscillation mode
- Apply suitable stabilization strategy
How to avoid parametric oscillations in combined amplifiers ???
Manufacture PAs with confidence
(and performances!)
Oscillations in RF Power Amplifiers

7. 7
-0.3 -0.2 -0.1 0.0 0.1 0.2 0.3
-6
-4
-2
0
2
4
6
Re (GHz)
Im(GHz)
Pole-Zero Identification
Node ‘n’
in s(i ,f )outv
RG
f0,
Pin
RL
10
30
-10
50
dB(Zsond)
2.0E9 4.0E9 6.0E9 8.0E9 1.0E100.0 1.2E10
-100
0
100
-200
200
frequency
phase(Zsond)
Freq (GHz)
|H|(dB)H(º)
poles
zeros
Pole-zero plot
( )H j
1
1
( )
( )
( )
n
i
i
p
j
j
s z
H s
s 







Frequency
domain
identification
techniques
STAN Tool
Complex conjugate poles with positive real part -> start-up of an oscillation
Oscillation frequency = Module of the imaginary part

8. 8
STAN Tool
J.M. Collantes et al. “Monte-Carlo Stability Analysis of Microwave Amplifiers”, 12th IEEE
Wireless and Microwave Technology Conference, April 2011, Florida.
A. Anakabe et al. “Automatic Pole-Zero Identification for Multivariable Large-Signal Stability
Analysis of RF and Microwave Circuits”, European Microwave Conference, September
2010, Paris.
J.M. Collantes et al. “Expanding the Capabilities of Pole-Zero Identification Techniques for
Stability Analysis”, IEEE Microwave Theory and Techniques International Symposium, June
2009, Boston.

9. 9
STAN Tool
Suitable for both linear and non-linear stability analysis
Very easy to use
Very easy to analyze results
Notion of “stability margin”
Oscillation mode knowledge -> Help to find the suitable
stabilization strategy
Parametric Analysis implemented
Monte-Carlo Analysis
Key Elements

10. 10
STAN Tool
Selecting the Node
Where to connect the probe for STAN analysis ?
SISO transfer function → exact
pole/zero cancellations are possible
Pole/zero cancellations are
associated with the lack of
controllability and/ or observability in
the system
real
imag
d
Pole-zero quasi-
cancellation
???

11. 11
STAN Tool
Physical quasi-cancellations
in s(i ,f )outv
this node has very low sensitivity to
that dynamics (low degree of
observability and/or controllability)
When part of the circuit dynamics is electrically isolated from the node selected for the
analysis, poles representing this dynamics appear quasi-cancelled by zeroes and the effect
of this dynamics on the transfer function is very slight

12. 12
STAN Tool
In multistage Circuits
Example of a three-stage PA exhibiting an oscillation
-0.3 -0.2 -0.1 0.0 0.1 0.2 0.3
-6
-4
-2
0
2
4
6
Re (GHz)
Im(GHz)
1_biasV _ 2biasV _3biasV
Connecting the probe to a node of the 3rd
stage, no instability is detected (we are
electrically isolated from where the actual
oscillation takes place).

13. 13
STAN Tool
In multistage Circuits
Connecting the probe to a node of
the 2nd stage → physical quasi-
cancellation (we still have low
sensitivity from the observation port)
-0.3 -0.2 -0.1 0.0 0.1 0.2 0.3
-6
-4
-2
0
2
4
6
Re (GHz)
Im(GHz)
Example of a three-stage PA exhibiting an oscillation
1_biasV _ 2biasV _3biasV

14. 14
STAN Tool
In multistage Circuits
Example of a three-stage PA exhibiting an oscillation
1_biasV _ 2biasV _3biasV
Connecting the probe to a node of the 1st stage →
The oscillation is clearly detected, unstable poles are
not quasi-cancelled with nearby zeros (high
sensitivity). We can conclude that the origin of the
oscillation is located in the 1st stage
-0.3 -0.2 -0.1 0.0 0.1 0.2 0.3
-6
-4
-2
0
2
4
6
Re (GHz)
Im(GHz)

15. 15
STAN Tool
Odd mode oscillation in combined amplifiers
Oscillation at f0/2 is very common in amplifiers with parallel
power combining structures
RG
f0,Pin
RL
RL
Q1
Q2
RG
f0,Pin
RL
RL
Q1
Q2
in s(i ,f )
outv
in s(i ,f )
outv
2e9 
 2e9
2e9 
 2e9
Odd mode
oscillation is not
detected at the
combining node.
Exact pole-zero
cancellation
Odd mode
oscillation is
clearly detected at
the gate of the
transistors

16. 16
STAN Tool
Odd mode oscillation in combined amplifiers
Powersplitter
Powercombiner
Power
splitter
Power
splitter
RL
RG
f0
Pin
1Q
2Q
3Q
4Q
G
A
B
C
D
E
F
1st step: analysis in nodes A, B and D
A B D
Oscillation
type
Preferred
strategy
x x x Even mode
- x -
Odd mode in
1st stage
- - x
Odd mode in
2nd stage
See next slide
- - - No oscillation -
Stabilization networks can be optimized using
parametric analysis -> find the best trade-off
between stability and RF performances
B,C
or/ and D, E, F, G
B
C

17. 17
Powersplitter
Powercombiner
Power
splitter
Power
splitter
RL
RG
f0
Pin
STAN Tool
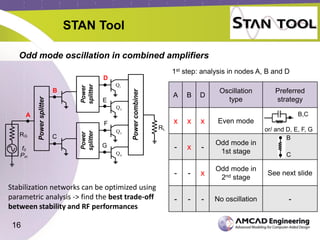
Odd mode oscillation in combined amplifiers
Test of the 4 branches with 4 probes, changing the phase
Odd mode oscillation
[ + - - +] or [ + - + - ]
 Q1 oscillates out of
phase with Q2, same for
Q3 and Q4
Powersplitter
Powercombiner
Power
splitter
Power
splitter
RL
RG
f0
Pin
Q1
Q2
Q3
Q4
Powersplitter
Powercombiner
Power
splitter
Power
splitter
RL
RG
f0
Pin
Q1
Q2
Q3
Q4
Powersplitter
Powercombiner
Power
splitter
Power
splitter
RG
f0
Pin
Q1
Q2
Q3
Q4
Powersplitter
Powercombiner
Power
splitter
Power
splitter
RG
f0
Pin
Q1
Q2
Q3
Q4
Odd mode oscillation
[ + + - - ]
 Q1 and Q2 oscillates out
of phase with Q3 and Q4
Powersplitter
Powercombiner
Power
splitter
Power
splitter
R
RG
f0
Pin
Q1
Q2
Q3
Q4
Powersplitter
Powercombiner
Power
splitter
Power
splitter
RG
f0
Pin
Q1
Q2
Q3
Q4Powersplitter
Powercombiner
Power
splitter
Power
splitter
RL
RG
f0
Pin

18. 18
STAN Tool
Performances Optimization
Example: Ku-Band MMIC PA for active space antenna
Stable original circuit
RF in RF out
RC stabilization
networks
Inter-branch
stabilization resistances
Natanael Ayllón Rozas
“Développement des méthodes de
stabilisation pour la conception des
circuits hyperfréquences : Application
à l’optimisation d’un amplificateur de
puissance spatial.”, PhD Thesis,
February 2011.

19. 19
STAN Tool
Performances Optimization
Example: Ku-Band MMIC PA for active space antenna
All stabilization networks removed
Parametric frequency
division /2 instability
RF in RF out
resistances maintained
for topological reasons

20. 20
STAN Tool
Performances Optimization
Example: Ku-Band MMIC PA for active space antenna
Optimized version
No oscillation detected,
especially around F0/2
RF in RF out
resistances maintained
for topological reasons
Stabilization
resistances

21. 21
STAN Tool
Performances Optimization
Example: Ku-Band MMIC PA for active space antenna
Results comparison
OptimizedOriginal

22. 22
Thank you
www.amcad-engineering.com
Contact information:
AMCAD Engineering
20 rue Atlantis
87069 Limoges, France
Stéphane Dellier
dellier@amcad-engineering.com
+33 555 040 531 / +33 672 371 046