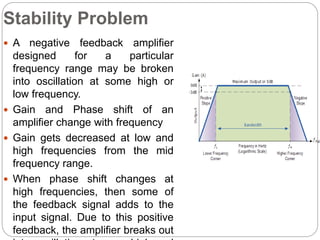
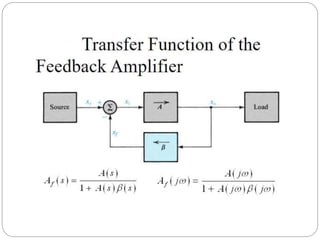
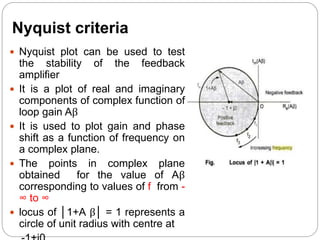
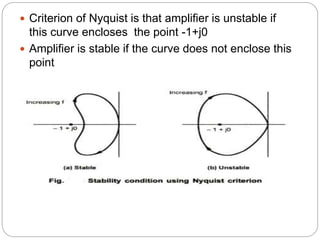
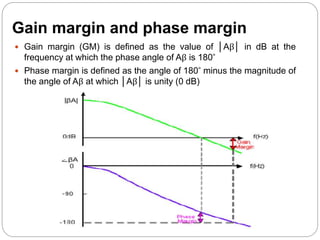
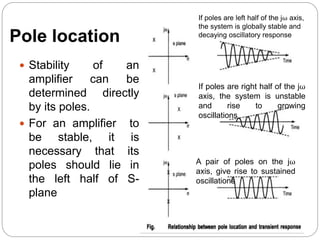
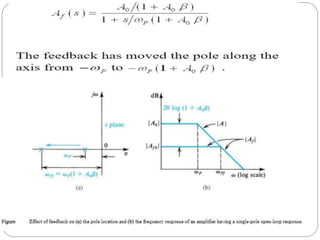
This document discusses stability problems in negative feedback amplifiers. It explains that amplifiers can become unstable if the phase shift exceeds 180 degrees at high frequencies, causing positive feedback. The Nyquist criterion and pole locations are introduced as ways to test stability. Gain and phase margins are also defined. Feedback is shown to shift poles left, improving stability for single and double pole amplifiers, but amplifiers with more poles could become unstable if phase shift exceeds 180 degrees.

1. Academic Year 2018-19
EC6401 Electronic Circuits II
Stability problems
Mrs.R.Chitra, AP/ECE,
Ramce Institute f Technology,
Rajapalayam

2. Stability Problem
 A negative feedback amplifier
designed for a particular
frequency range may be broken
into oscillation at some high or
low frequency.
 Gain and Phase shift of an
amplifier change with frequency
 Gain gets decreased at low and
high frequencies from the mid
frequency range.
 When phase shift changes at
high frequencies, then some of
the feedback signal adds to the
input signal. Due to this positive
feedback, the amplifier breaks out

5. Contd....
 Stability of feedback amplifier is depend on the
loop gain
 The frequency at which phase angle become
180˚, loop gain A(jω)β(jω) will be real number with
a negative sign.
 Thus at this frequency, the feedback will become
positive, it will behave like an Oscillator.

6. Nyquist criteria
 Nyquist plot can be used to test
the stability of the feedback
amplifier
 It is a plot of real and imaginary
components of complex function of
loop gain Aβ
 It is used to plot gain and phase
shift as a function of frequency on
a complex plane.
 The points in complex plane
obtained for the value of Aβ
corresponding to values of f from -
∞ to ∞
 locus of │1+A β│ = 1 represents a
circle of unit radius with centre at

7.  Criterion of Nyquist is that amplifier is unstable if
this curve encloses the point -1+j0
 Amplifier is stable if the curve does not enclose this
point

8. Gain margin and phase margin
 Gain margin (GM) is defined as the value of │Aβ│ in dB at the
frequency at which the phase angle of Aβ is 180˚
 Phase margin is defined as the angle of 180˚ minus the magnitude of
the angle of Aβ at which │Aβ│ is unity (0 dB)

9. Pole location
 Stability of an
amplifier can be
determined directly
by its poles.
 For an amplifier to
be stable, it is
necessary that its
poles should lie in
the left half of S-
plane
If poles are left half of the jω axis,
the system is globally stable and
decaying oscillatory response
If poles are right half of the jω
axis, the system is unstable
and rise to growing
oscillations
A pair of poles on the jω
axis, give rise to sustained
oscillations

10. Effect of feedback amplifiers on
poles

12.  The pole of amplifier is shift towards left from
imaginary axis and it never enters the right-
half of the s-plane.
 Single pole amplifier introduce a maximum
phase shift of 90˚
 Because of this, a single pole amplifier s
stable for any values of β and hence such an
amplifier is also known as unconditionally
stable amplifier

13. Amplifier with two pole response
Maximum phase shift is 180˚ (90˚ per pole).
However, this phase shift is reached at ω = ∞ and
hence he feedback of amplifier is always negative
for entire frequency range

14.  If Feedback amplifier has more than two
poles, the phase angle of loop gain could
exceed 180˚ beyond certain frequency, then
amplifier cab be unstable.

15. References:
 Sedra and Smith, “Micro Electronic Circuits”;
Sixth Edition, Oxford University Press, 2011.
 Jacob Millman, ‗Microelectronics‘, McGraw Hill,
2nd Edition, Reprinted, 2009.