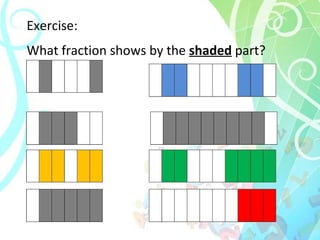
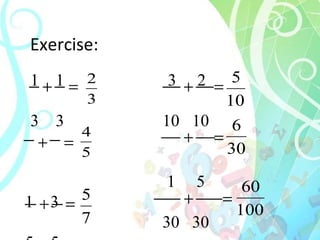The document provides instructions and materials for a 6th grade math project on fractions. It includes objectives, materials needed, how to make the project, rubric for grading, and content about fraction meanings, equivalent fractions, comparisons, operations, and exercises. The content is organized into sections covering key fraction concepts.

1. FRACTION

2. MATH- PROJECT- GRADE 6- FRACTION Objective/s: Students understand about the lesson- Fraction Students can use their creativity to find the way/s to understand fraction concept Materials: An after used calender (Wall/ desk), contains 6 or more pages Colour paper (Origami/ Spectra/ etc) or colour pencil/ marker Decoration- If needed How to make: Each page must contain the knowledge about fraction Student must include minimum 6 items Student must include the drawing/ picture about each item and the question and answer example

3. MATH- PROJECT- GRADE 6- FRACTION Due date: Tuesday, 9 August 2011 Fraction: Meaning Equivalent Fraction Reduction to lowest term Comparison Fraction Improper Fractions and Mixed Numbers Adding/ Subtracting Fraction with the same denominator Adding/ Subtracting Fraction with different denominator Whole Mixed Number Operation Multiplying Fraction Dividing Fraction

4. MATH- PROJECT- GRADE 6- FRACTION RUBRIC: CRITERIA 7-8 5-6 3-4 1-2 Techniques The student has demonstrated thorough competence when choosing and using techniques/materials and equipment. The student is able to choose and use the techniques, materials &/or equipment competently. The student is able to use the techniques, materials &/or equipment adequately. The student has difficulty using the techniques, materials &/or equipment. Design Specification The student has displayed excellent understanding of the design specification and has fully justified any modifications used. Student has shown good understanding of the design specification and was able to make necessary modifications to enhance the finished product. The student has demonstrated adequate understanding of the design specifications. Did not demonstrate any use of modifications to enhance final product. The student has demonstrated little understanding of the design specification. Procedure The student is fully able to understand and follow procedures and alter them where necessary. The student usually understands and follows correct procedures. The student sometimes has difficulty understand &/or following procedures. The students usually has difficulty understanding &/or following procedures. Finished Product The student produced an outstanding finished product. The student produced a well-made and well-presented product. The student produced a finished product which was of an adequate standard and quality. The student produced a finished product that was of a poor standard and low quality.

5. MEANING • One marble out of five marbles • Two marbles out of six marbles

6. • Three parts out of 4 equal parts MEANING • One part out of 3 equal parts

7. Numerator and Denominator • Numerator • Denominator 3 4

8. Exercise: What fraction shows by the shaded part?

9. Exercise: What fraction shows by the Unshaded part?

10. Exercise: Worksheet 9.1 and 9.3

11. Equivalent Fraction Blue part = ½ What will happen if we divided the Blue part by 2?

12. Equivalent Fraction Blue part = ½ Blue part = We can say that, to make an equivalent fraction: If we multiplied the Numerator by 2 , We must multiplied the Denominator by 2

13.     2 .... 3 12 2 14 3 .... 2 2  4 8 3 12 12 2 14 14 3 3  7 21 Equivalent Fraction

14.     Reduction to lowest term 21 .... 24 1. Divide with the denominator 2. Divide with HCF (Highest Common Factor) of 21 and 24 is 3. 4 .... 12 4 1 12 3 21 7 24 8

15. Comparison of Fraction Let us compare fraction : and 1. a. Make a list of equivalent fractions from each

16. Comparison of Fraction Let us compare fraction : and b. We choose the same denominator between each equivalent fractions

17. Comparison of Fraction Let us compare fraction : and c. Then compare those two fractions <

18. Comparison of Fraction Let us compare fraction : and 2. Short cut: “Cross Multiplication Method” 4 x 12 = 48 7 x 8 = 56 Because 48 is smaller than 56 so, <

19. Exercise: Worksheet 9.8 and 9.9

20. Improper Fractions and Mixed Numbers Proper Fraction , The Numerator smaller than the denominator Example: Improper Fraction , The Numerator greater than the denominator Example: Mixed Numbers , The sum of a whole number and a fraction Example:

21.  Addition of Fraction with the same denominator 2 1 5 5 1 5

22.       Exercise: 3 2 10 10 1 5 30 30 7 53 100 100 1 1 3 3 1 3 5 5 2 3 7 7

23.       Exercise: 3 2 10 10 1 5 30 30 7 53 100 100 1 1 3 3 1 3 5 5 2 3 7 7

24.   1 1 3 2 1 3 2 6   1 2 3 6   2 6 3 5 6 6 Addition of Fraction with different denominator

25.   1 1 2 4 1 2 2 4   1 4 1 4   2 4  1 4  2 1 3 4 4 4 Addition of Fraction with different denominator

26.  Mutiply the denominator 3 x 2 = 6 1 1 3 2 Addition of Fraction, Short Cut

27.   2 3 7 11 2  11  3  7 43 7  11 77 Addition of Fraction, Short Cut

28.       Exercise: 1 1 3 2 1 1 3 5 1 1 5 2 1 1 4 2 1 1 3 6 1 1 8 7

29.       Exercise: 1 1 3 2 1 1 3 5 1 1 5 2 1 1 4 2 1 1 3 6 1 1 8 7

30. 3 3  ? • Fraction as Division : Saundra has 1 cake , She wants to give the cake equally to 3 people , What is the fraction for the parts of those people? If each person get 1  3 So the fraction for the whole parts is : “ WHOLE”

31. 5 5  ? • Fraction as Division : Tiara has 1 cake , She wants to give the cake equally to 5 people , What is the fraction for the parts of those people? If each person get, 1  5 So the fraction for the whole parts is : “ WHOLE”

32. 5 5  ? • Fraction as Division : Erika has 2 cakes , She wants to give the cake equally to 4 people , What is the fraction for the parts of those people? If each person get, 2  4 So the fraction for the whole parts is : “ WHOLE”

33. Mixed Numbers Operation- Addition Add the number of the two fractions: 1 + 1 = 2 Add the fractions of the two fractions: Add the answers : 2 + 1 = 3

34. Mixed Numbers Operation- Addition Add the number of the two fractions: 1 + 1 = 2 Add the fractions of the two fractions: Add the answers : 2 + =

35. Mixed Numbers Operation- Subtraction Subtract the number of the two fractions: 2-1 = 1 Subtract the fractions of the two fractions: The answers : 1 and =

36. Mixed Numbers Operation- Subtraction Subtract the number of the two fractions: 3 - 1 = 2 Subtract the fractions of the two fractions: Add the answers : 2 and = 1 + - =

37. Exercise: Worksheet 8.8 and 8.12

38. Multiplication Fraction with Number 1 2  4  1  4): 2  2

39.  1 1 2 2 Multiplication Fraction with Fraction

40.  In mind : I have 1/6 than I take ½ from 1/6, So I get 1/12 1 1 2 6 Multiplication Fraction with Fraction

41. Multiplication Fraction with Fraction (Short Cut- to find the lowest term) 1 3 1 6 1 1 1 4

42. Exercise: Worksheet 9.2 and 9.5

43. Divided Fraction- With Number • 1/2 : 2 = ? If we divide ½ the answer is 1/4 • 1/3 : 2 = • 2/3 : 2 = • ¾:3= • 4/5 : 3 = • 7/9 : 3= • 20/25 : 5 =

44. Divided Fraction- With Number • 1/2 : 2 = ? If we divide ½ the answer is 1/4 • 1/3 : 2 = • 2/3 : 2 = • ¾:3= • 4/5 : 3 = • 7/9 : 3= • 20/25 : 5 =

45. Pembagian Pecahan • Berapa 1/2 : 2 = ? Berapa kali 2 hasilnya ½? Jawab 1/4

46. 1 1 : 2 6  1 6 1 2 Divided Fraction- With Fraction In mind: How many in ? 3

47. Divided Fraction- With Fraction (Short Cut)

48. Divided Mixed Number- With Fraction

49. Divided Mixed Number- With Fraction Exercise: Worksheet 7.4 and 7.5

50. Fraction Exercise: CB pg. 24- 25 Mrs. Ong repacks 2 kg of seasoning powder into small packets. Each packet contains kg of seasoning powder. How many packets does she get? Answer: 2 : = 2 x = 10 So, Mrs. Ong will get 10 packets

51. Fraction Exercise: CB pg. 24- 25 3. What is the greatest number of m pieces that you can cut from a 3- metre length of raffia? Answer: 3 : = 3 x = = 5 So, 5 is the greatest number of pieces