SSII2020 チュートリアルセッション TS1
6/10 (水) 9:45~10:55 メイン会場 (vimeo + sli.do)
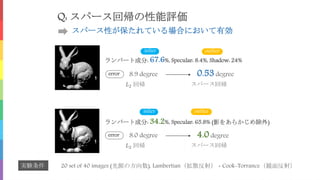
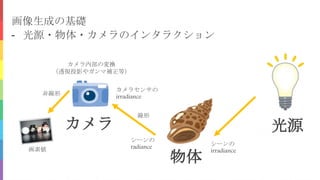
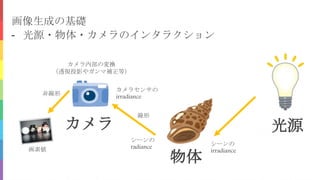
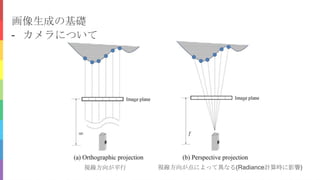
物理ベースビジョンとは、画像生成を物理・光学現象として捉え、それに基づいて画像から被写体の形状や材質を復元するコンピュータビジョンの一分野である。代表的なものには、1枚の陰影画像から被写体の形状を復元するシェープフロムシェーディング法や複数枚の陰影画像を利用するフォトメトリックステレオ法がある。本チュートリアルでは、1980年代から存在する物理ベースビジョンの基本的な考え方と基礎技術、および近年の研究動向について解説する。












![- 物体表面での光のふるまいをモデル化
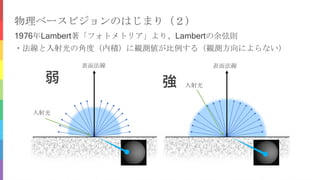
鏡面反射
拡散反射
表面下散乱
屈折・透過
• BRDF(反射)
• BTDF(透過)
• BSDF(反射+透過)
• BSSRDF(散乱面反射)
Bidirectional [X] Distribution Function
BSDFとBSSRDFの違い
BSDFはあくまでも単一点における反射方向における光の割合を表したもの
BSSRDFは異なる2点間での関係性を示したもの
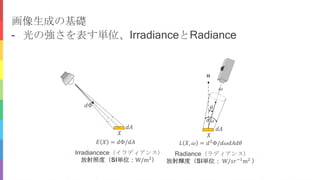
画像生成の基礎](https://image.slidesharecdn.com/ts1-200605045326/85/SSII2020TS-16-320.jpg)


























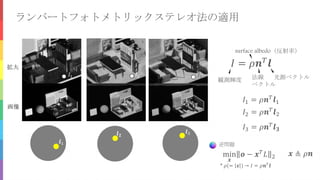
![ランバートフォトメトリックステレオ法の適用(結果)
復元された法線 復元された反射
率
参考入力画像
*法線のカラーマッピング 127 * ([nx, ny, nz] +
1)](https://image.slidesharecdn.com/ts1-200605045326/85/SSII2020TS-46-320.jpg)