Download to read offline
Uploaded byAndrey Urusov
Моделирование ТПиПП
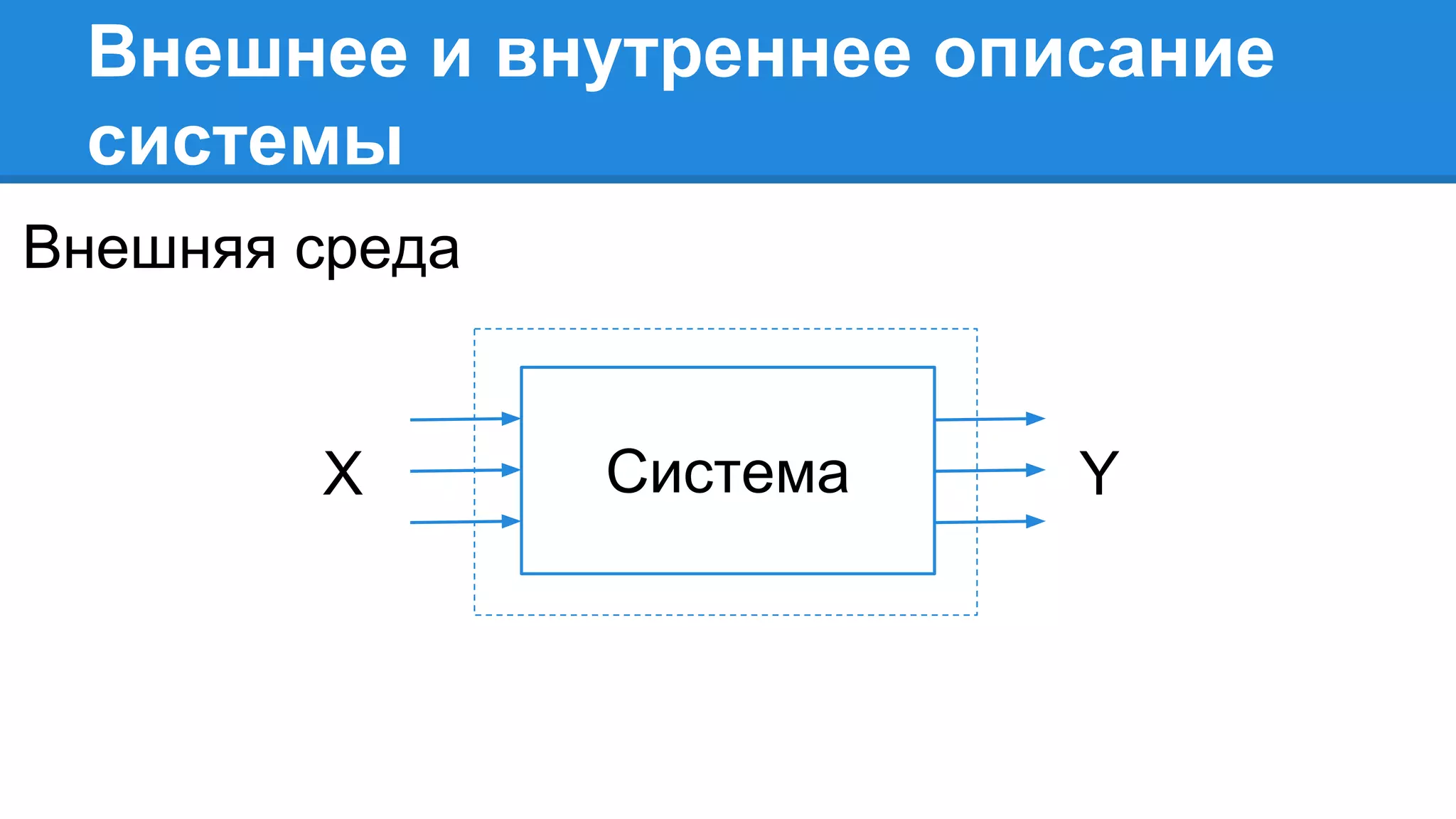
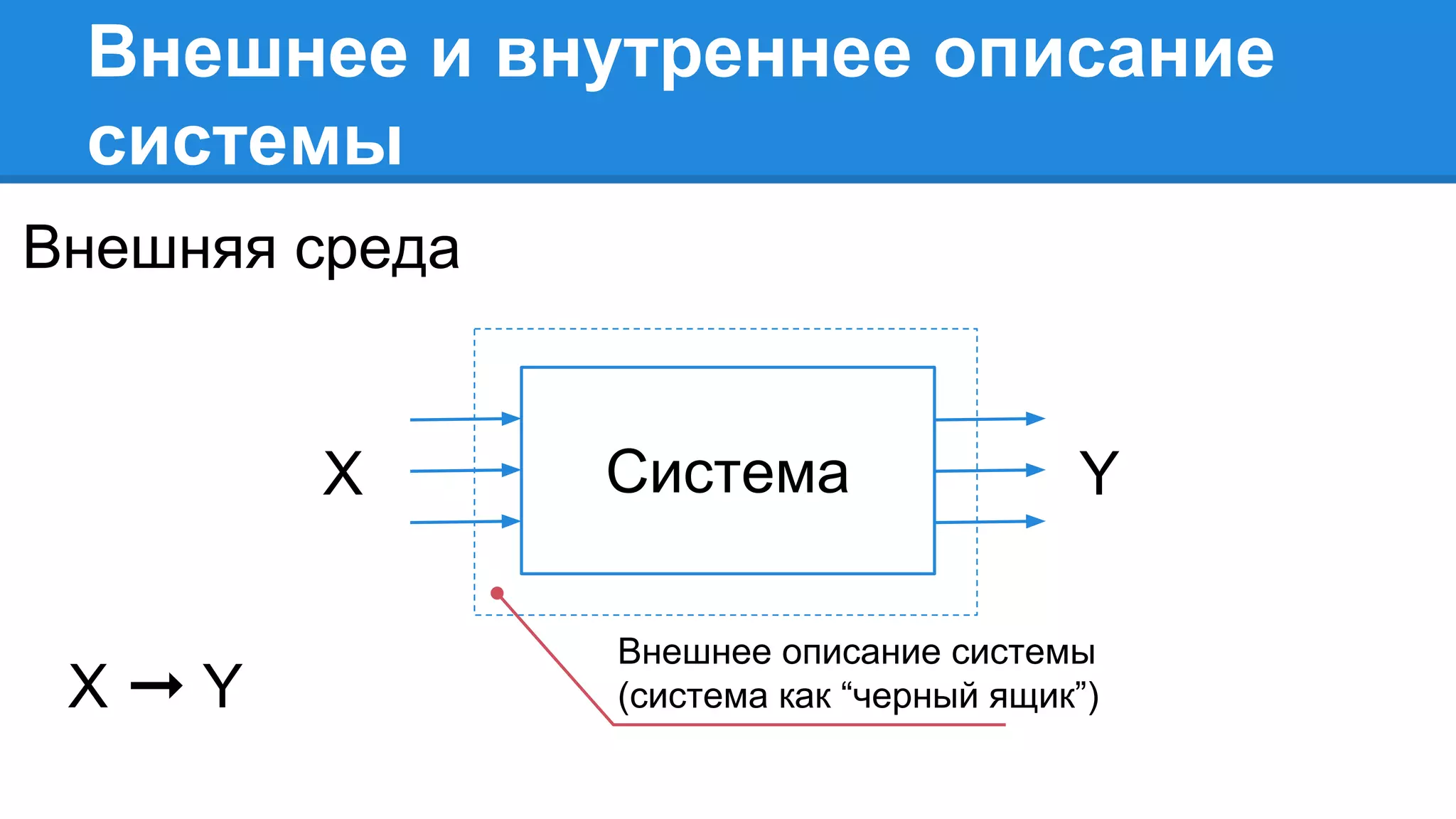
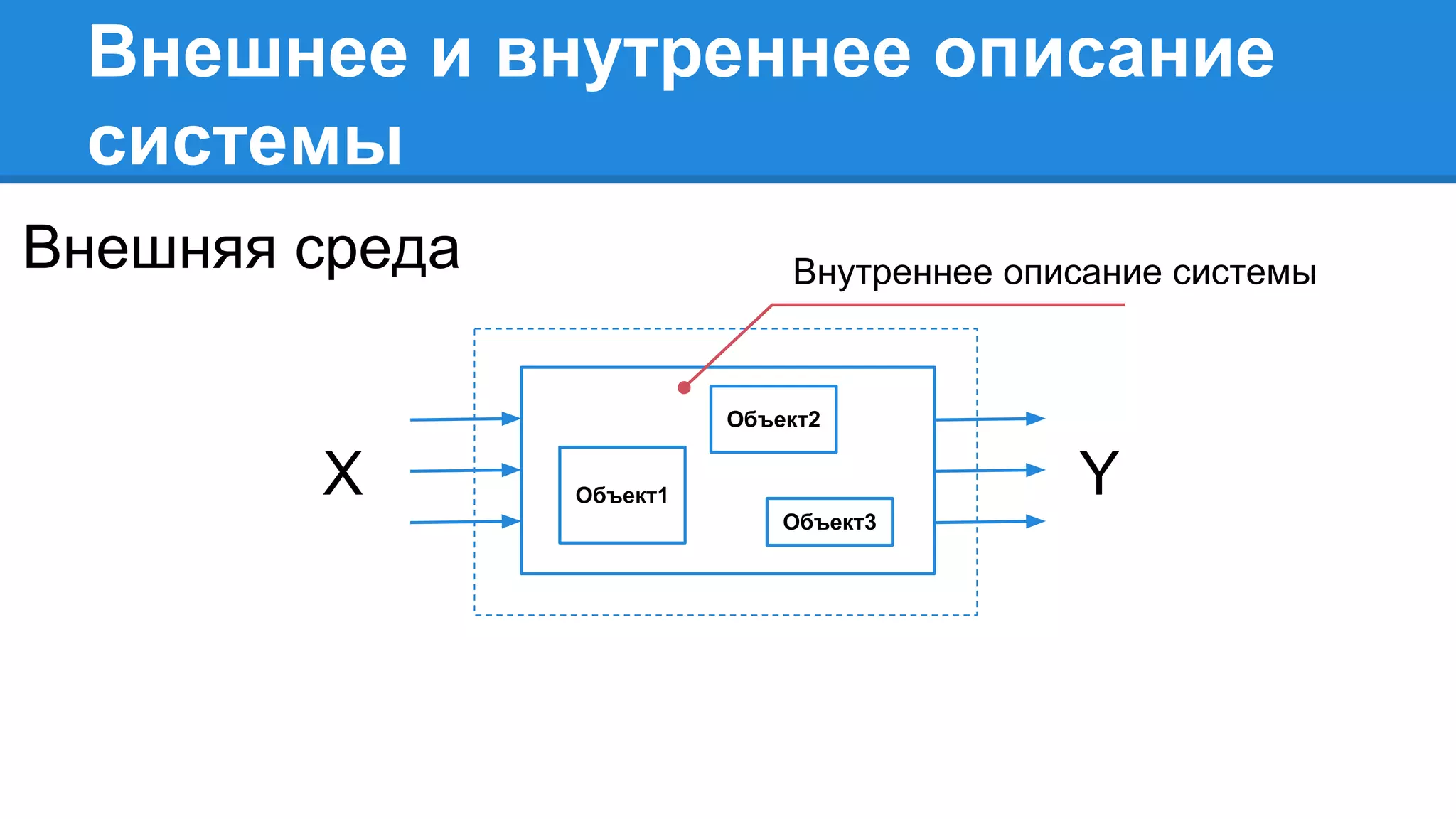
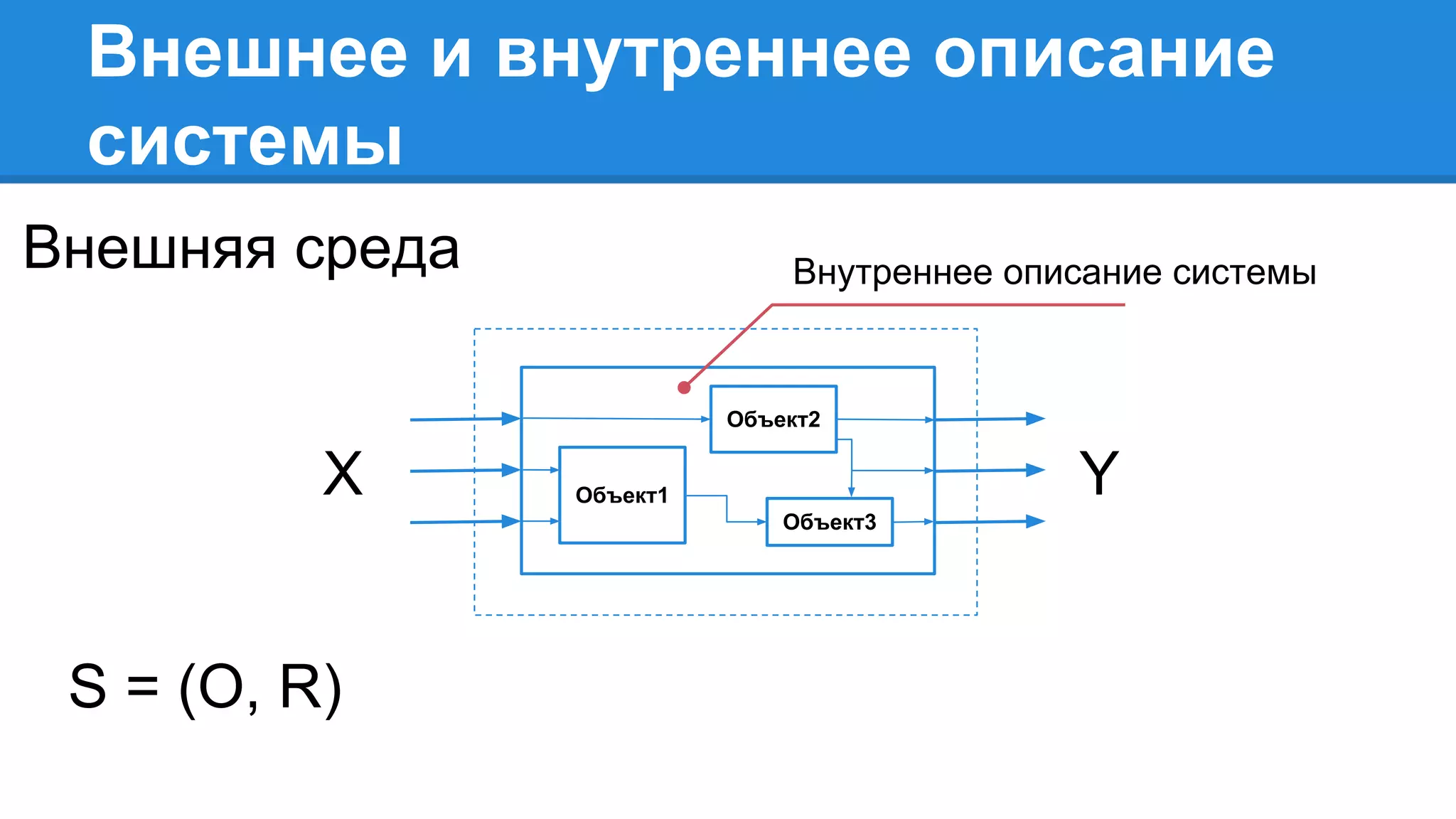
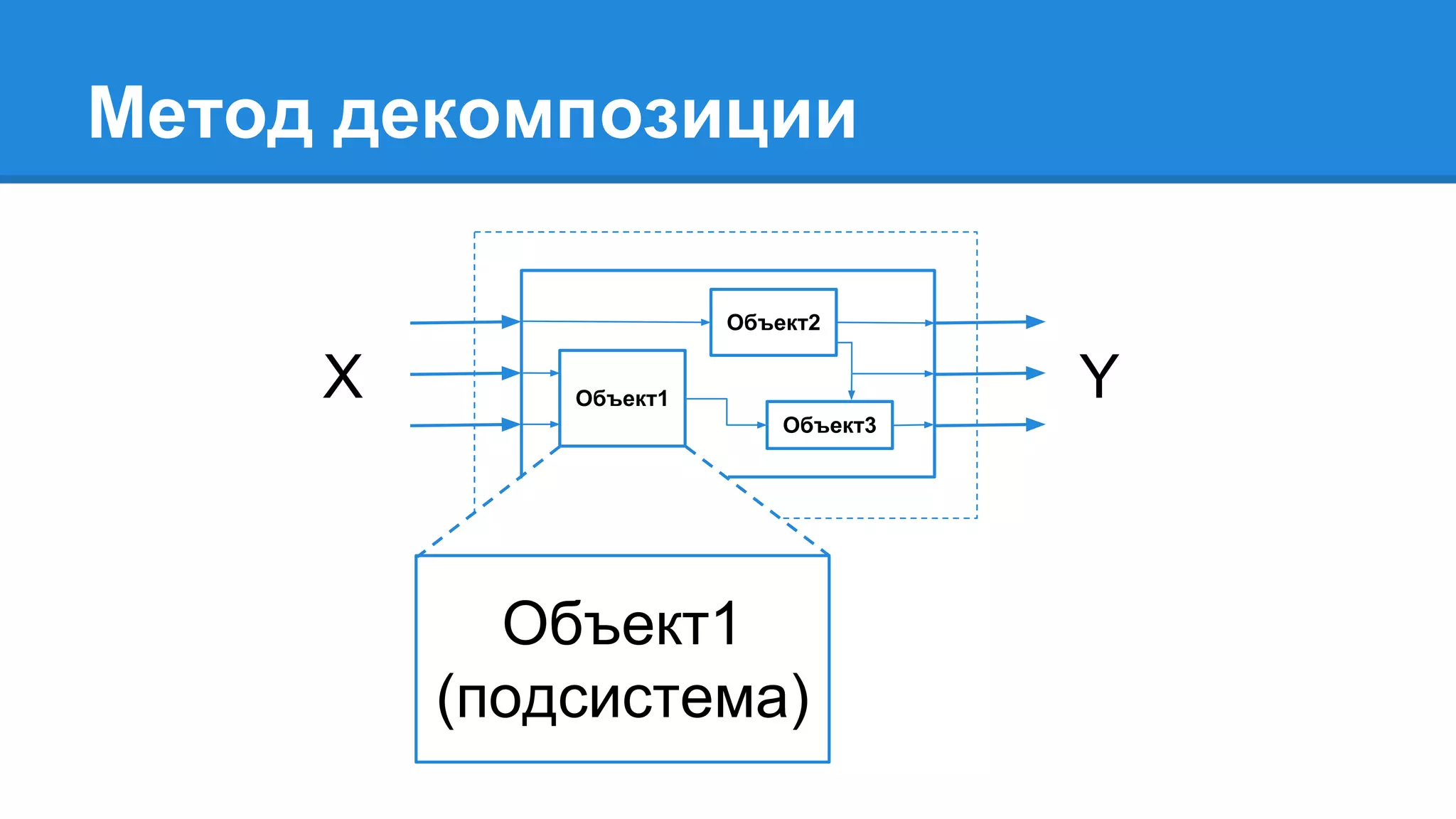
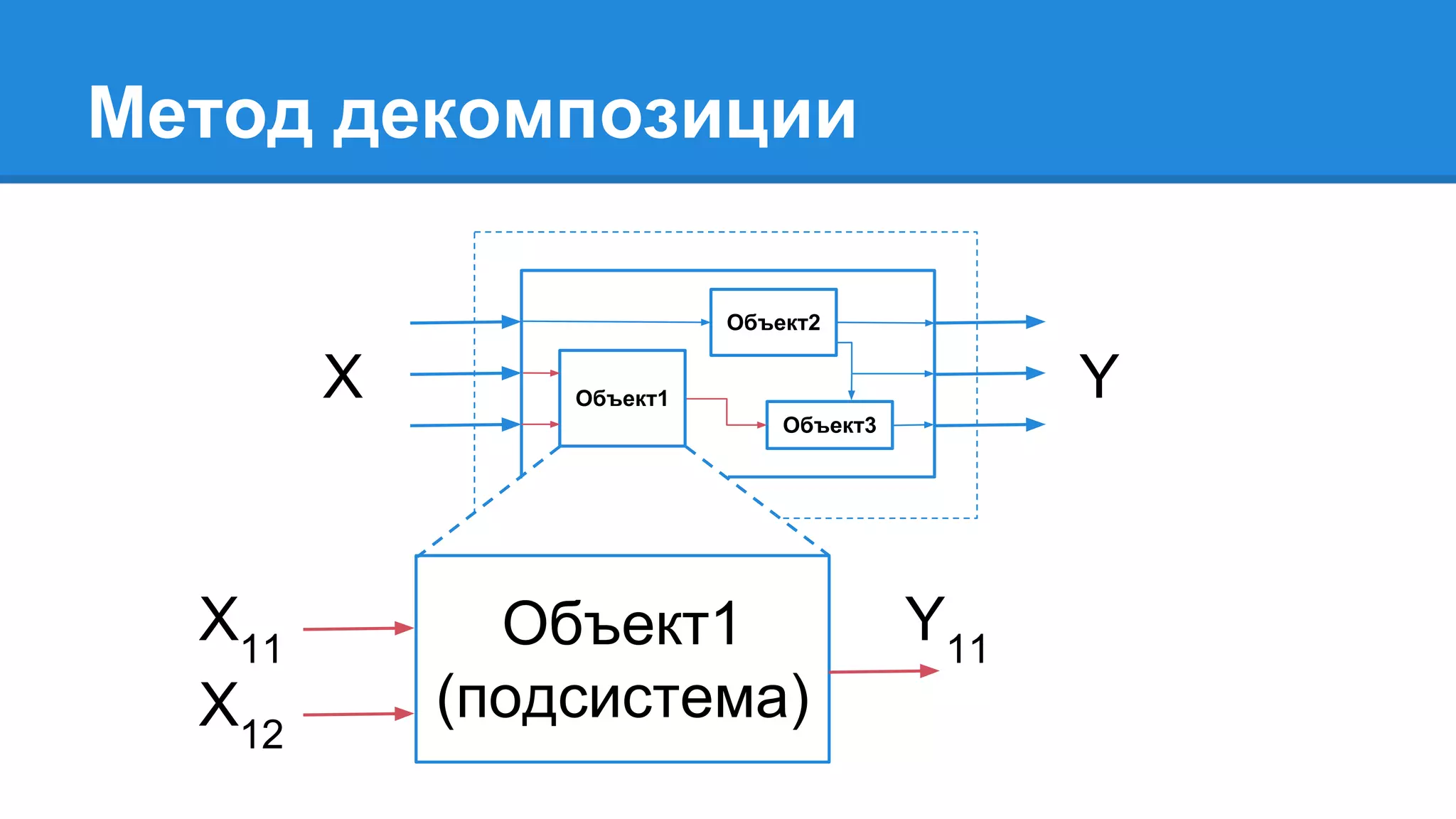
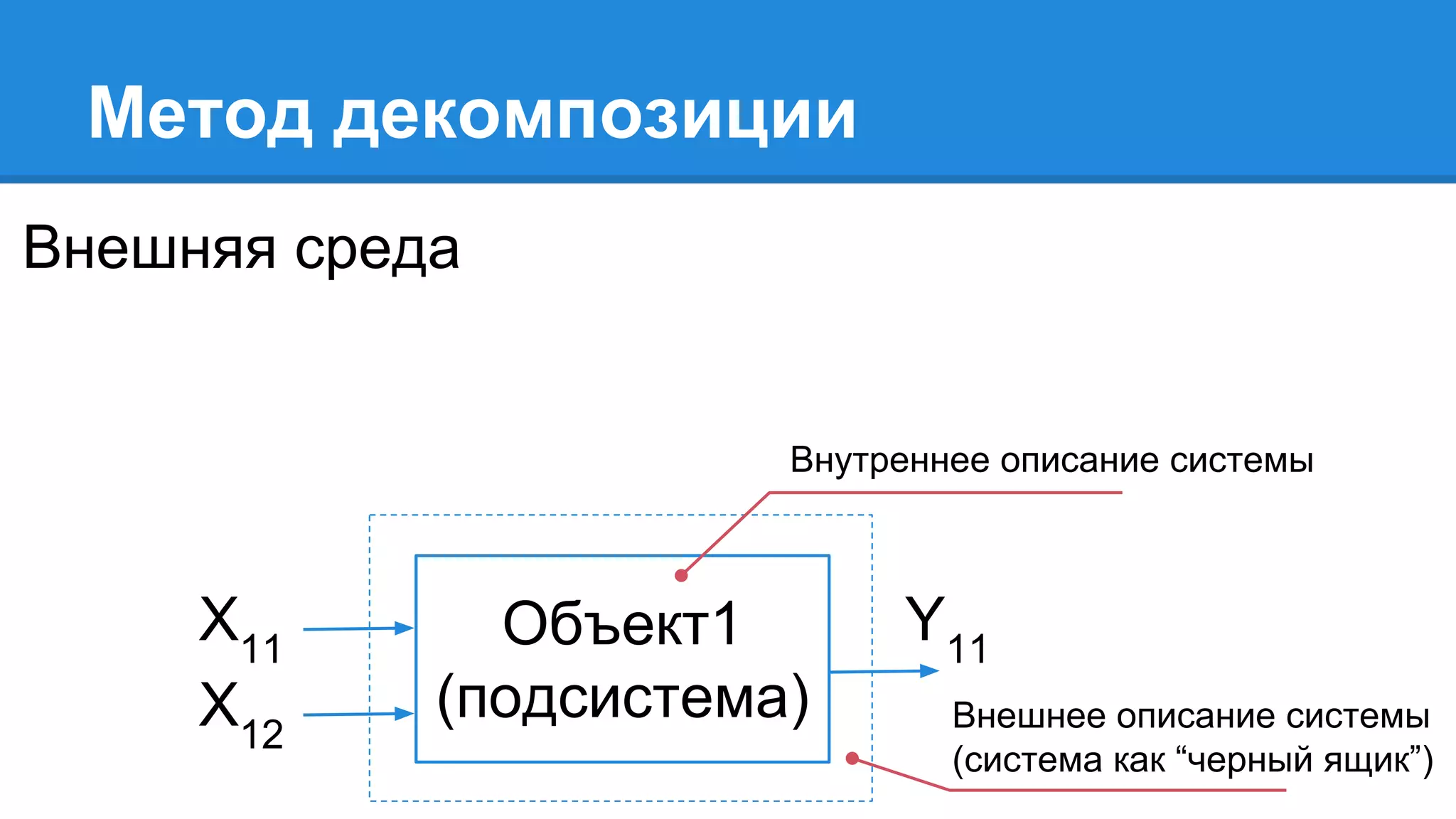
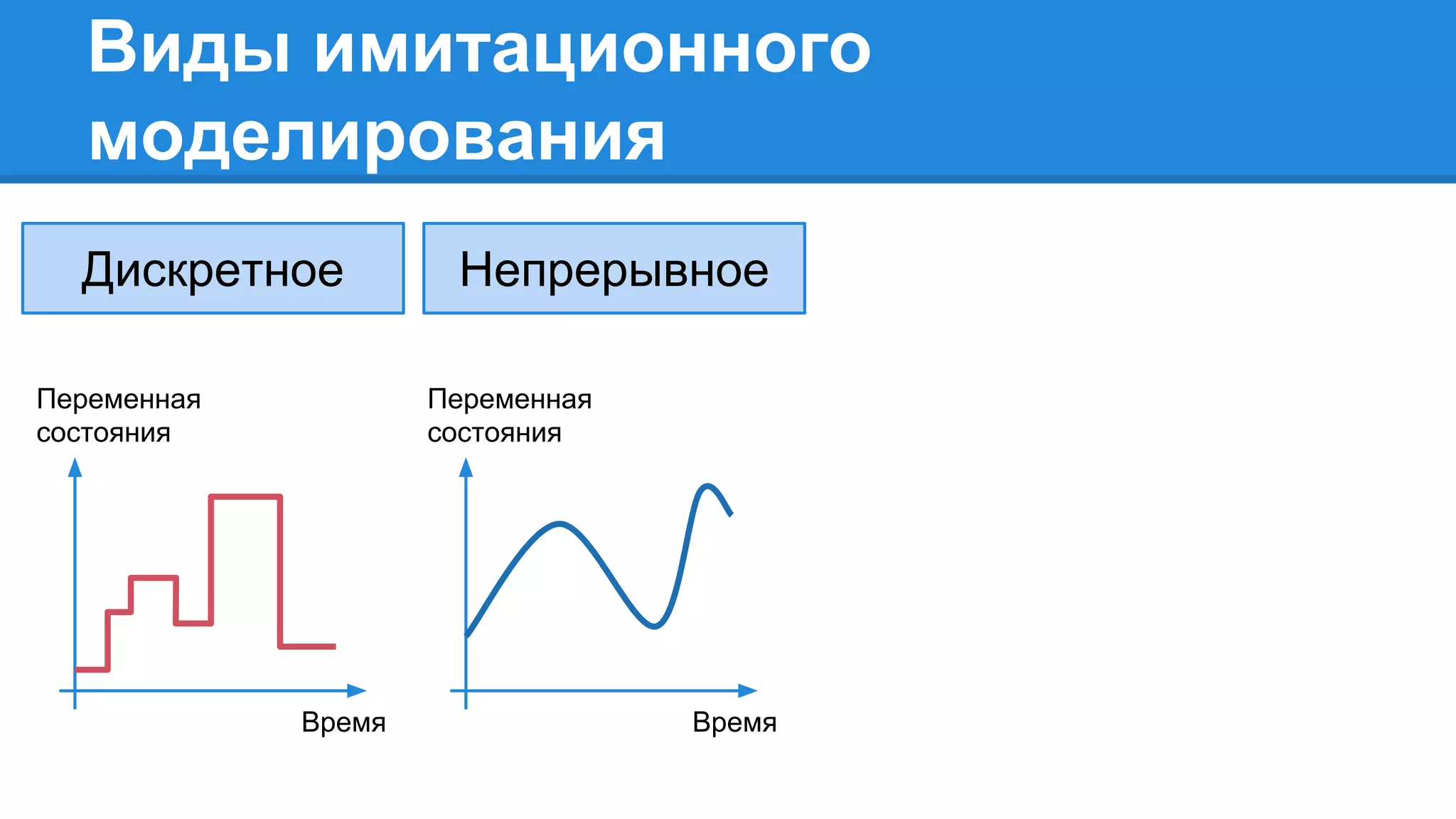
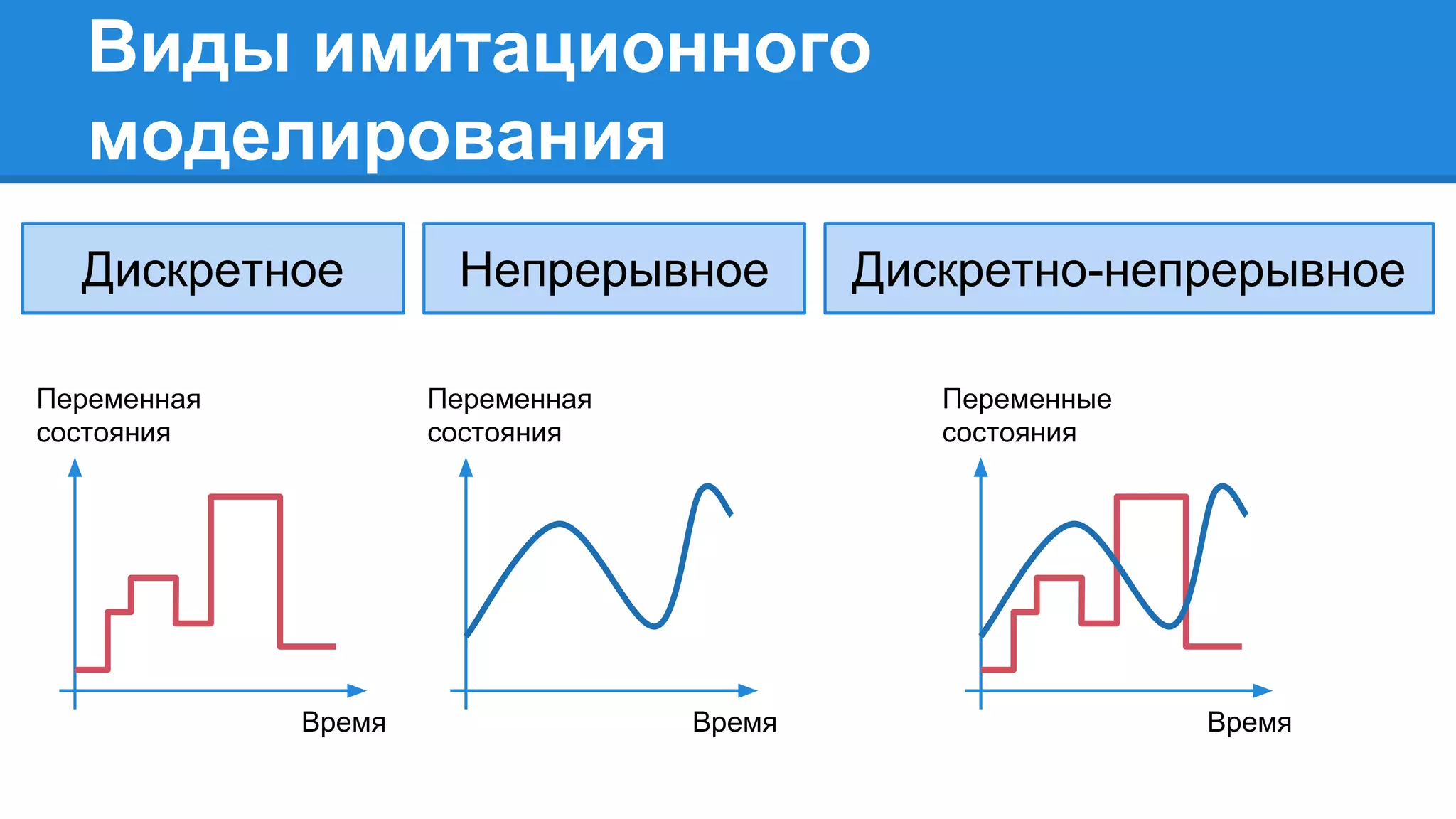
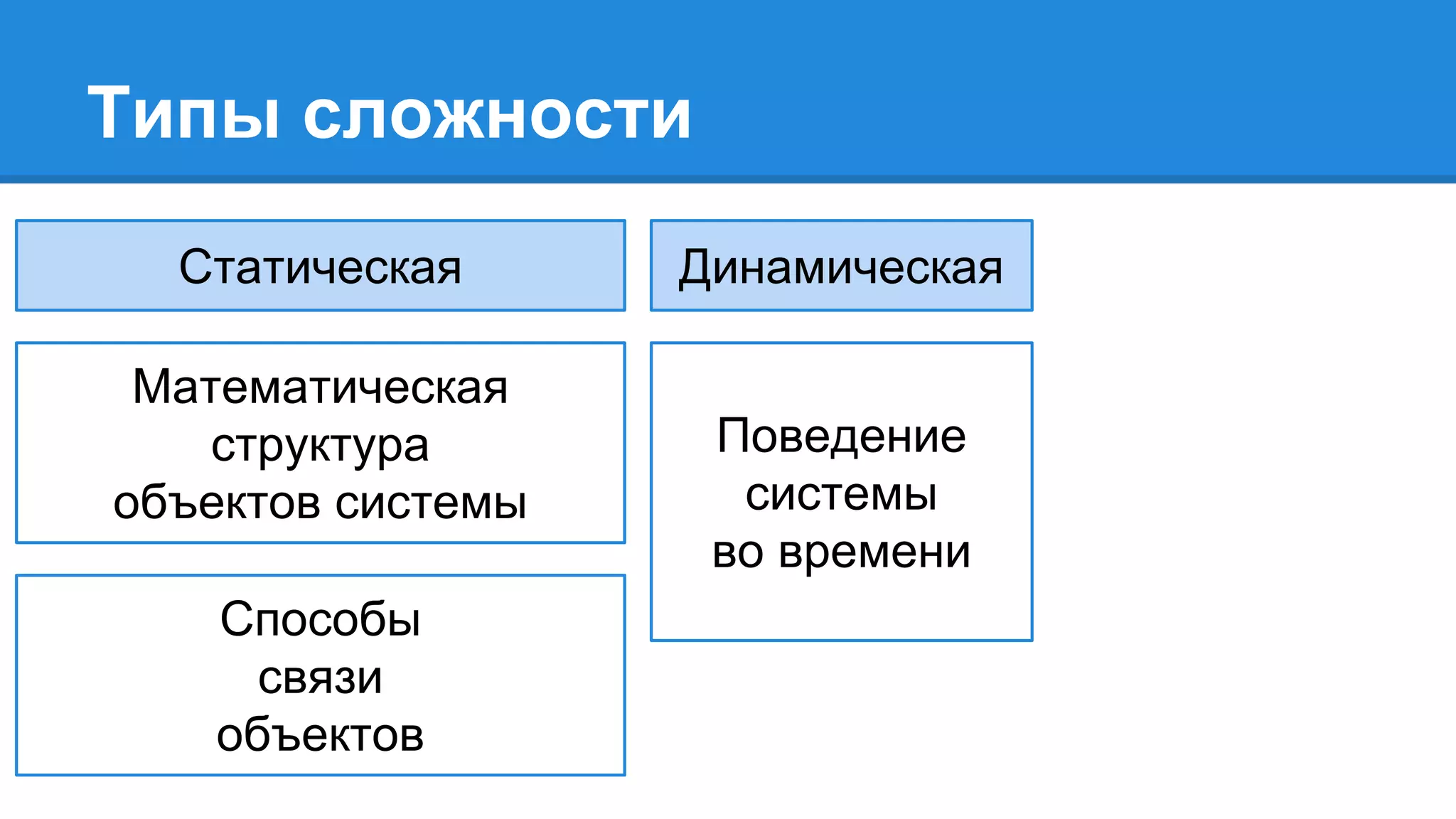
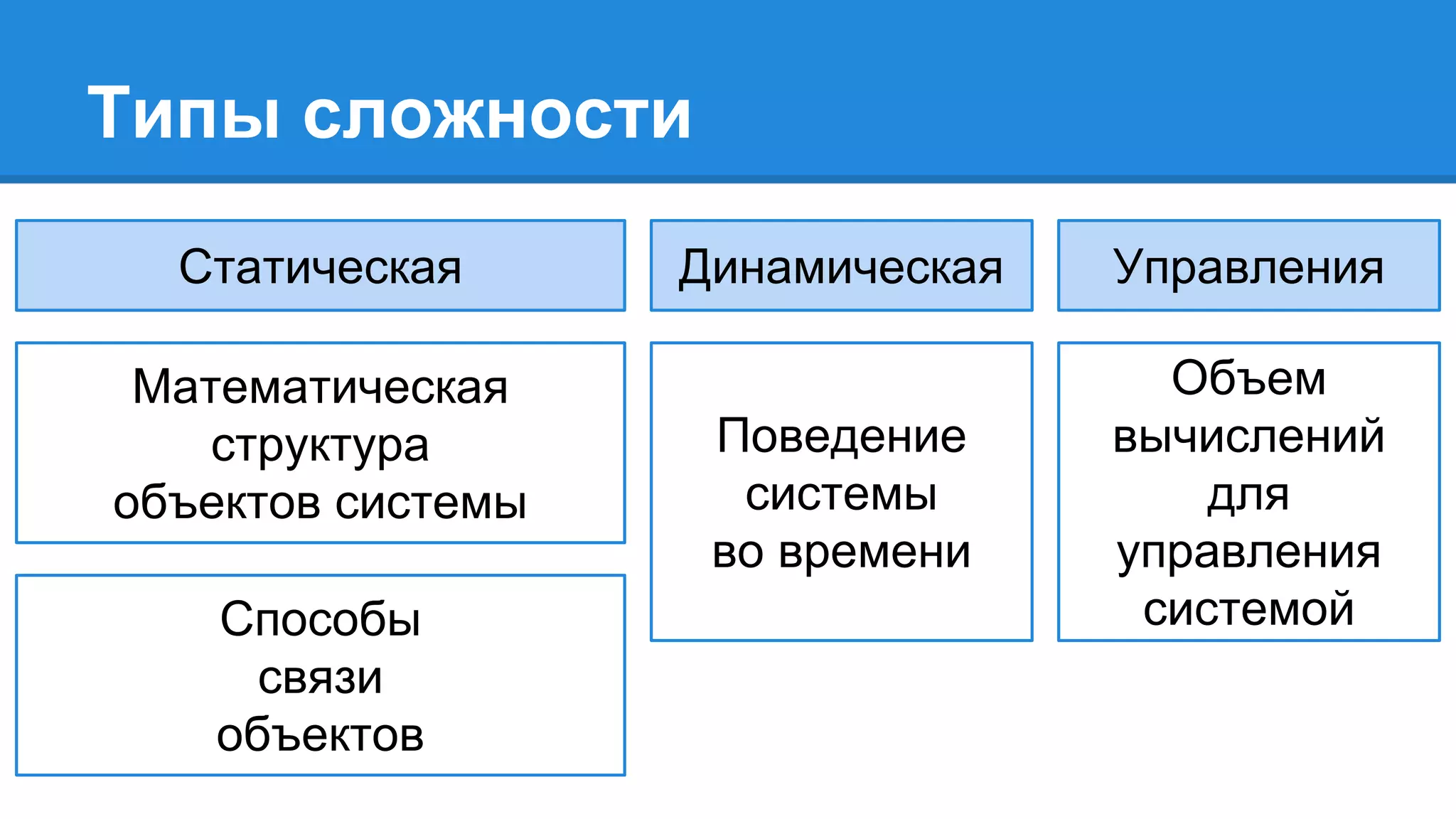
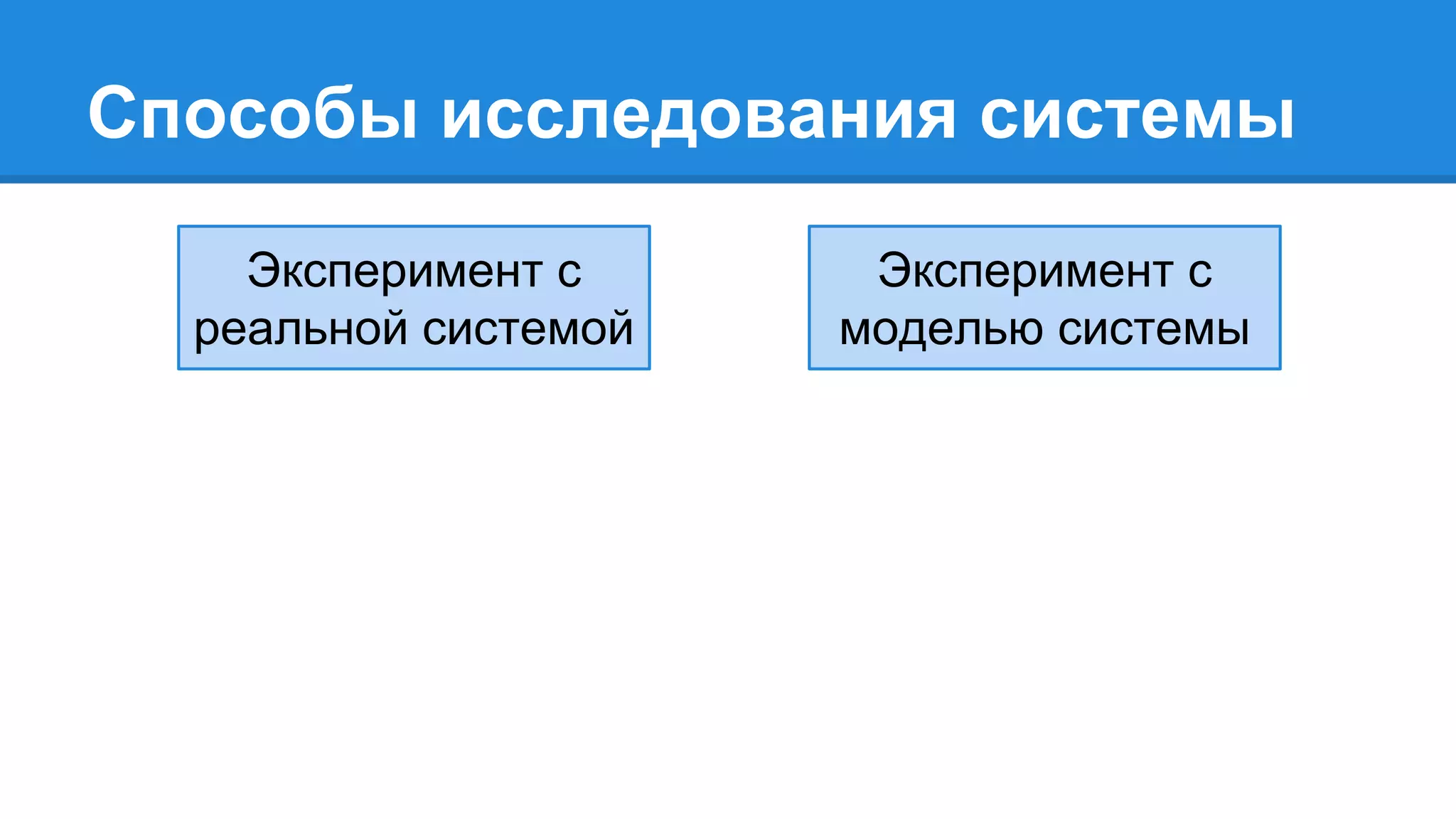
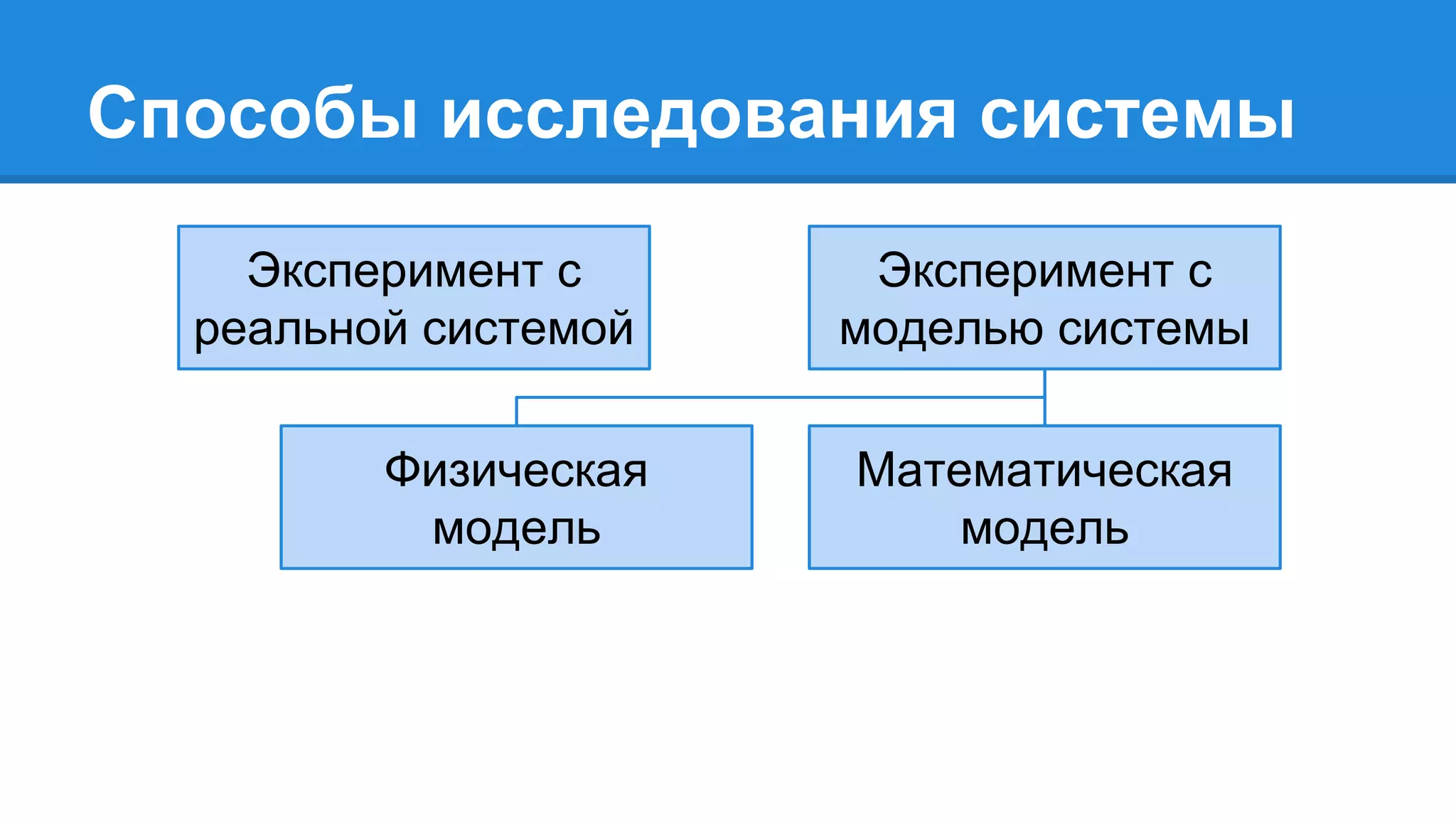
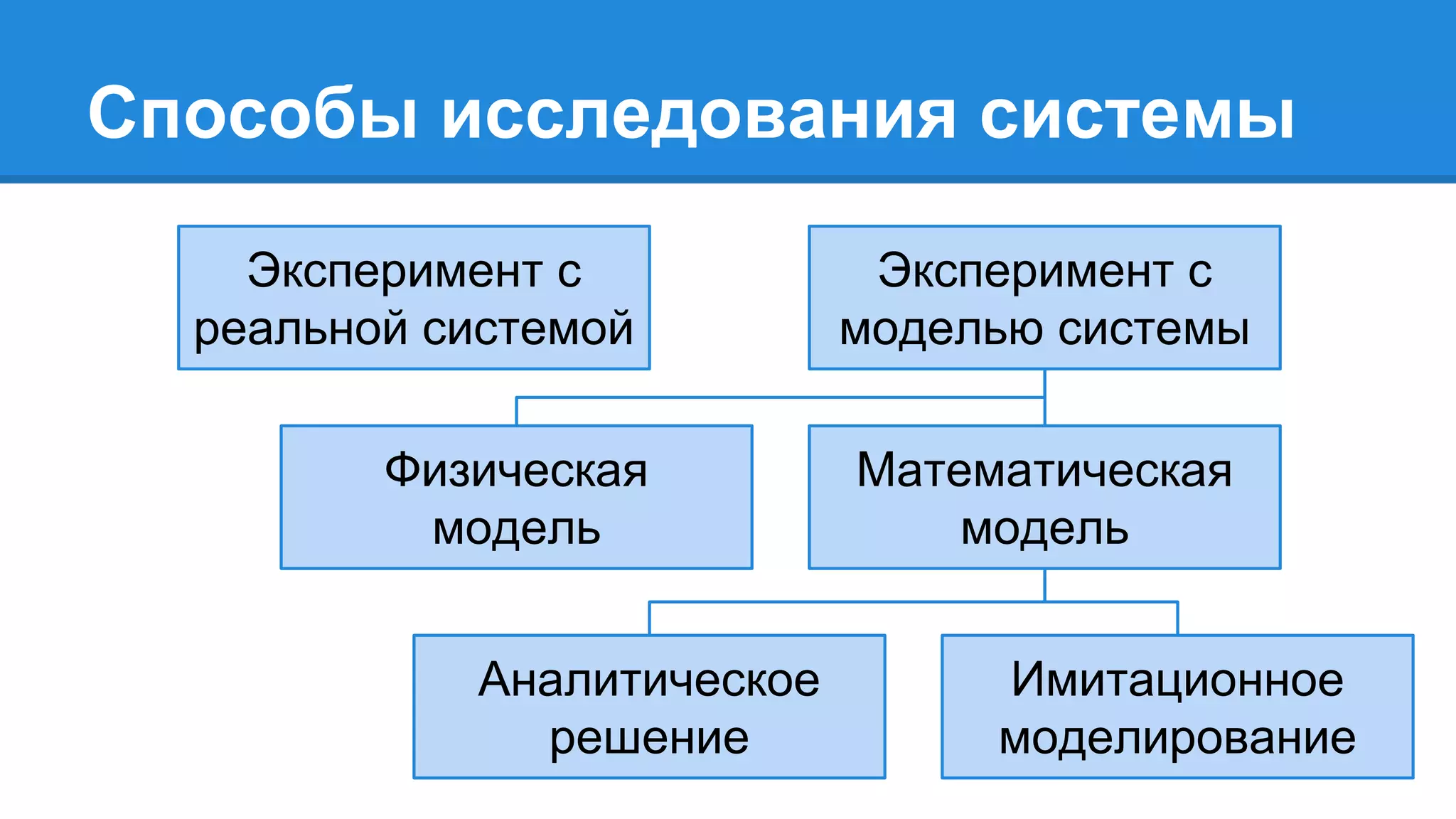
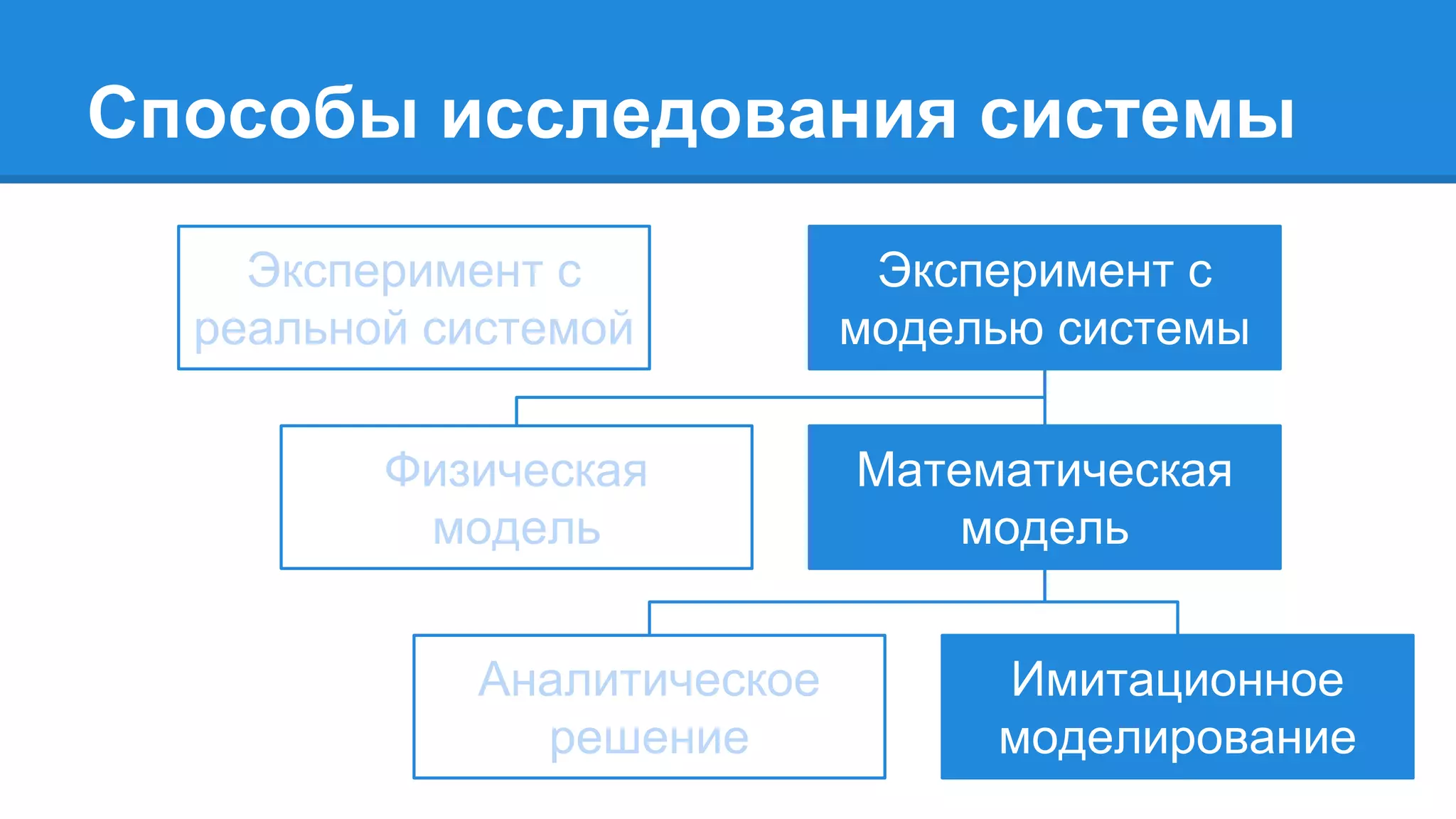
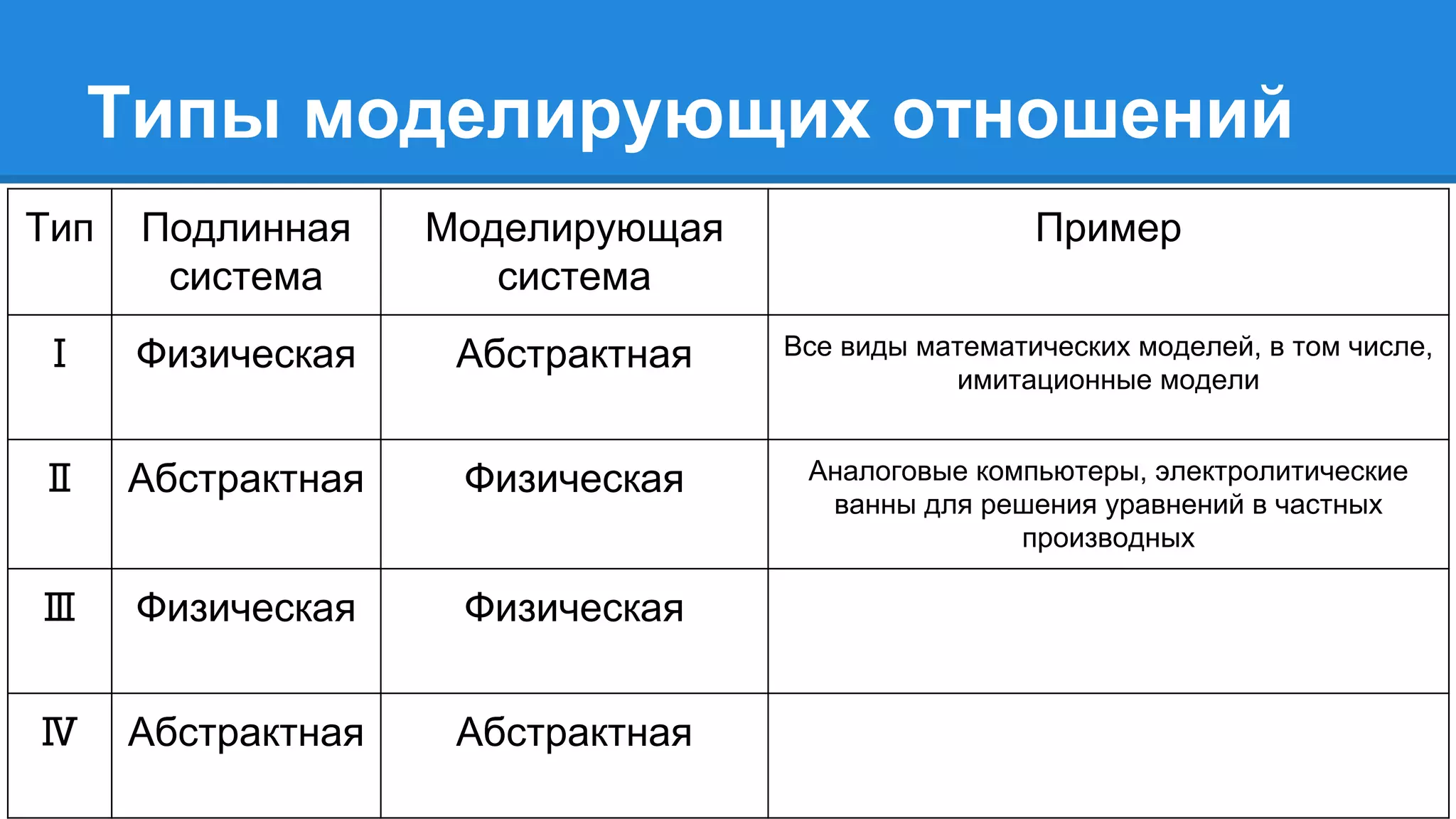
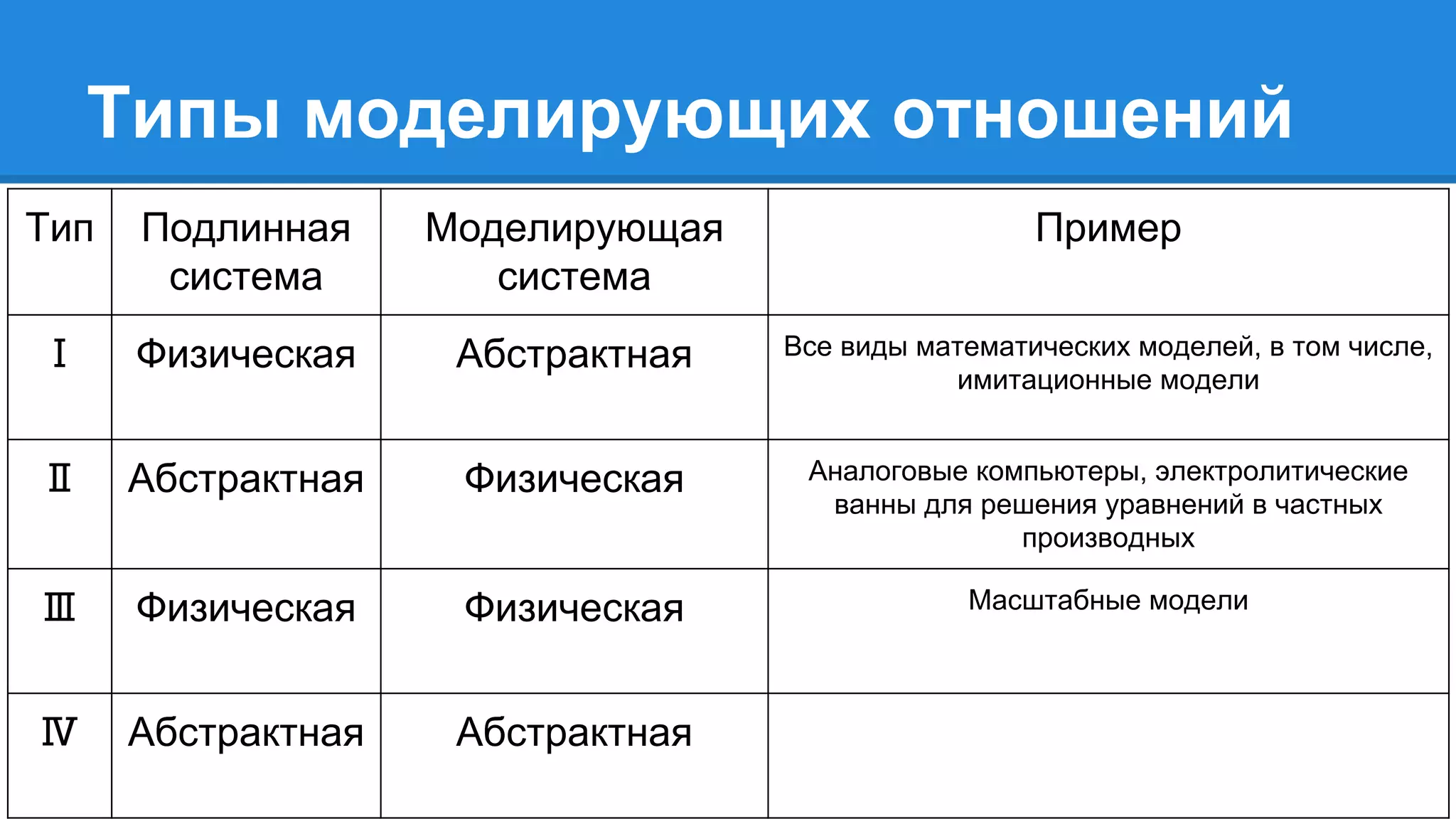
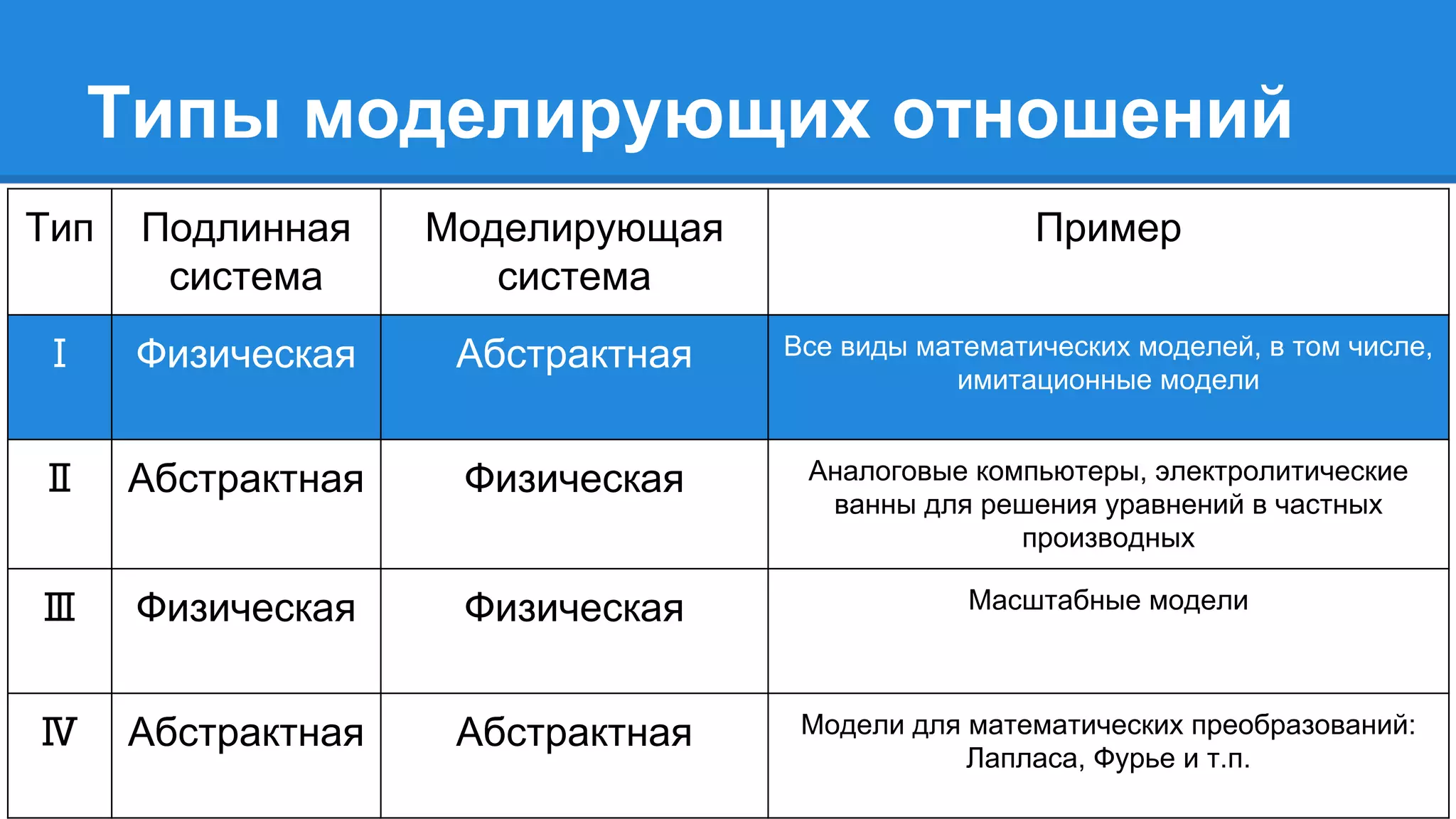
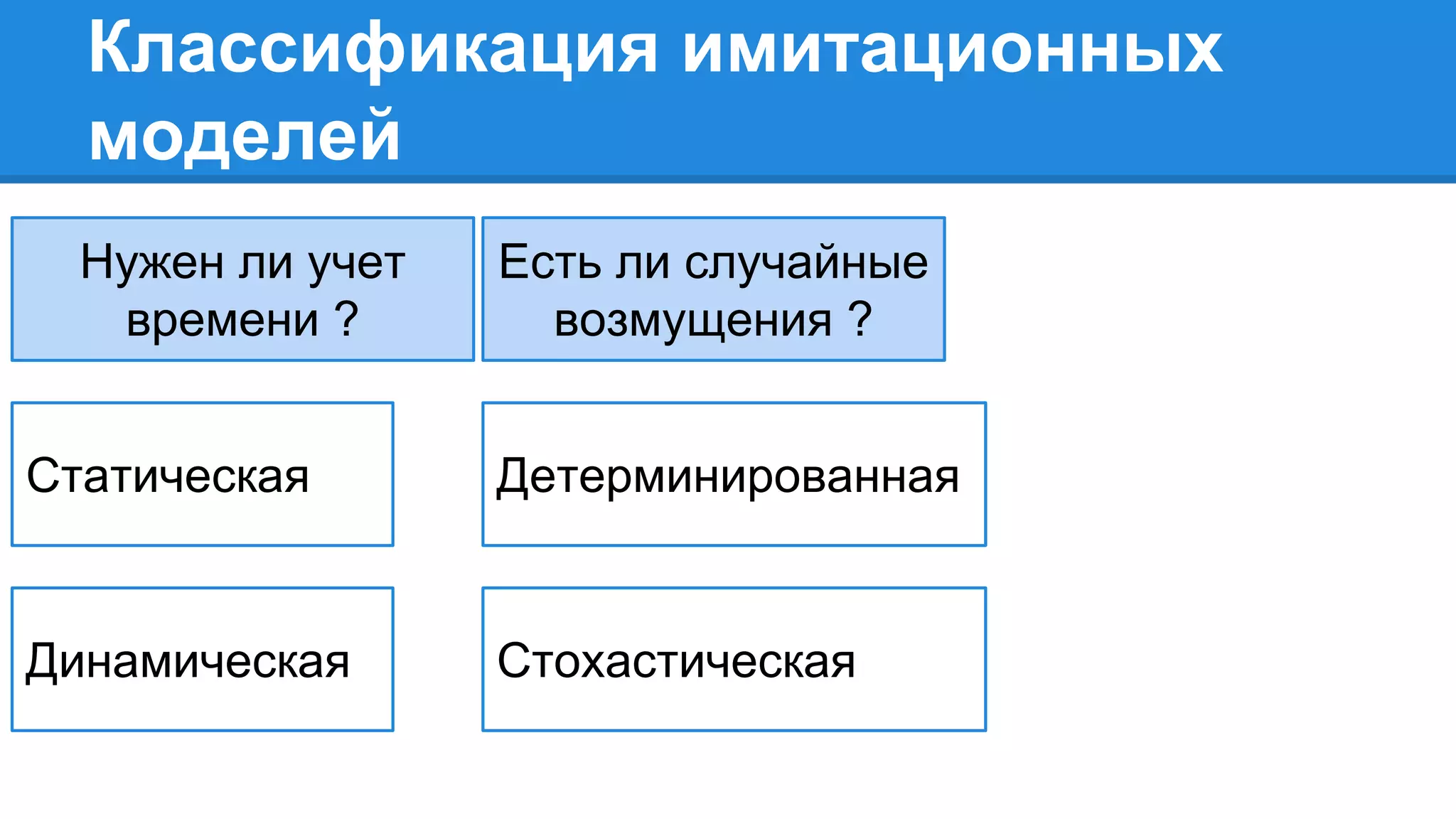
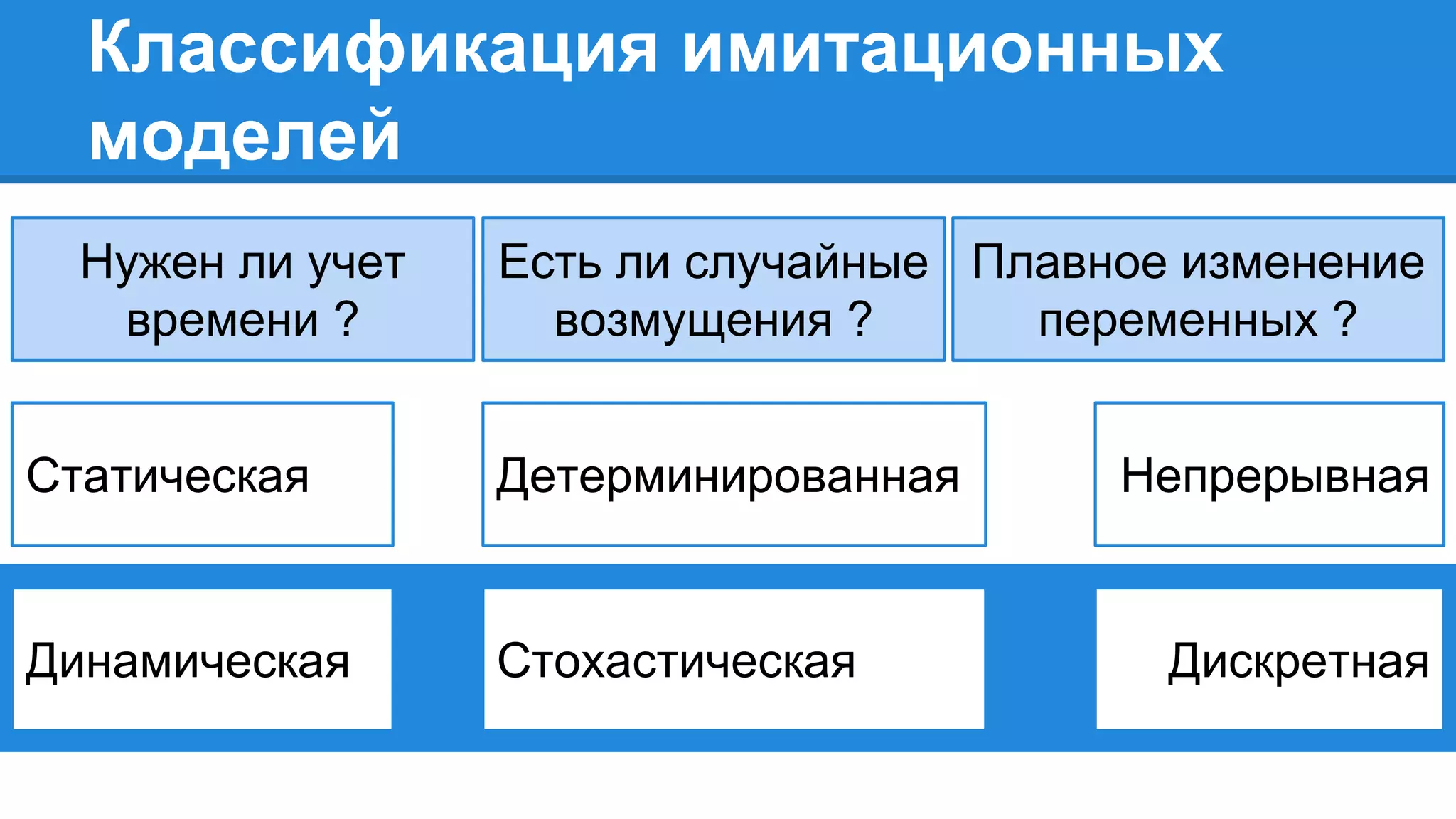
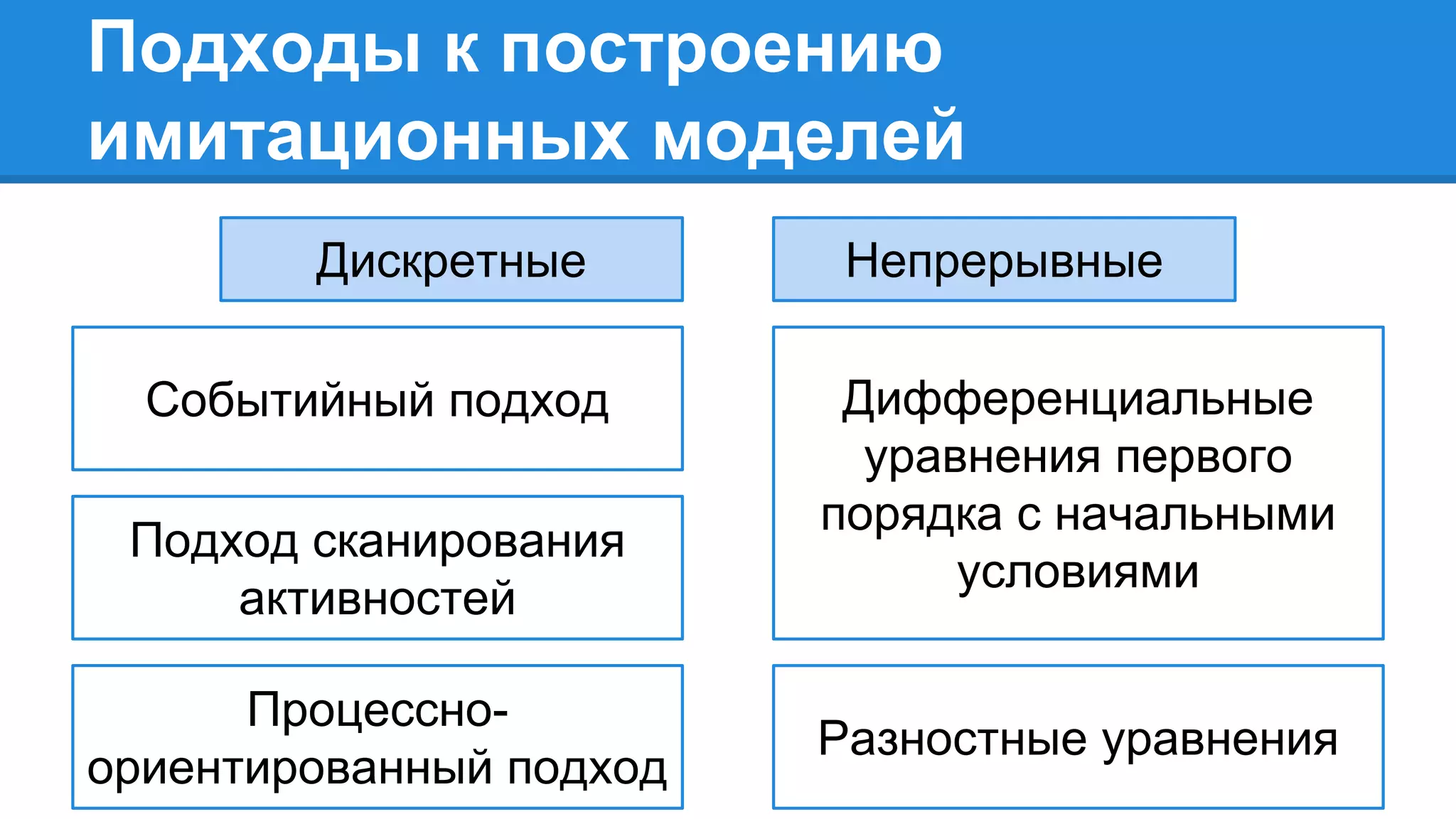
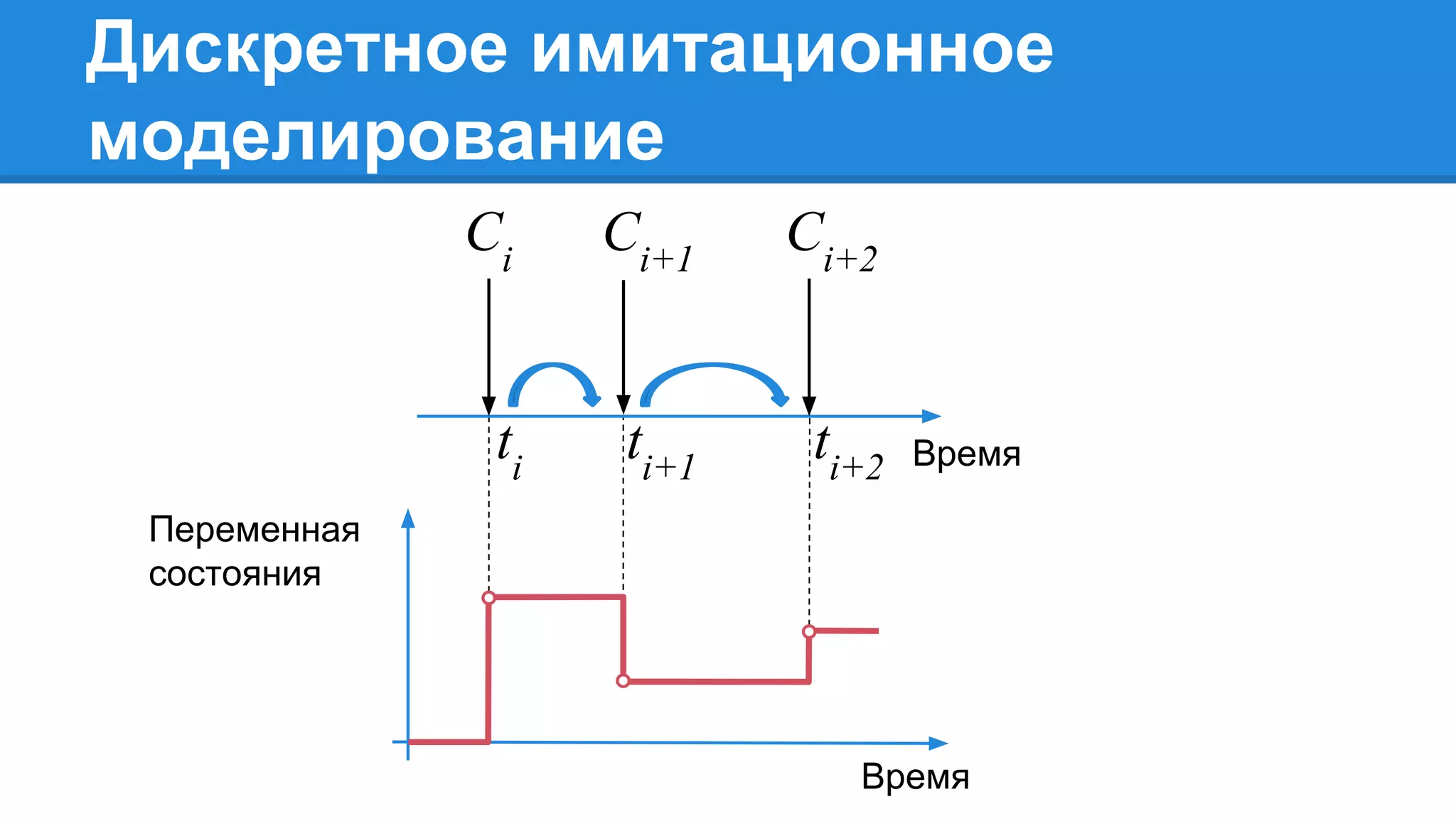
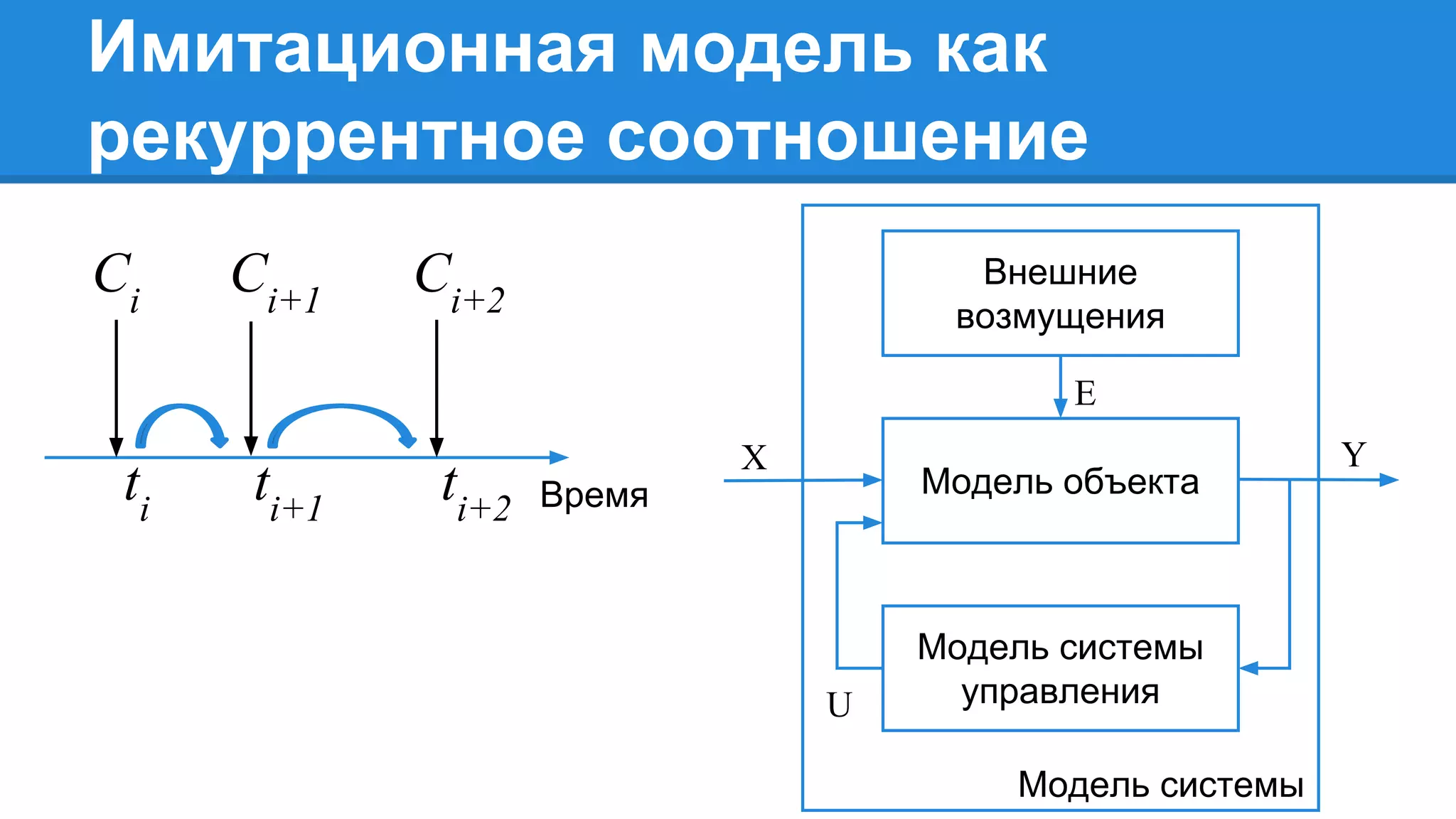
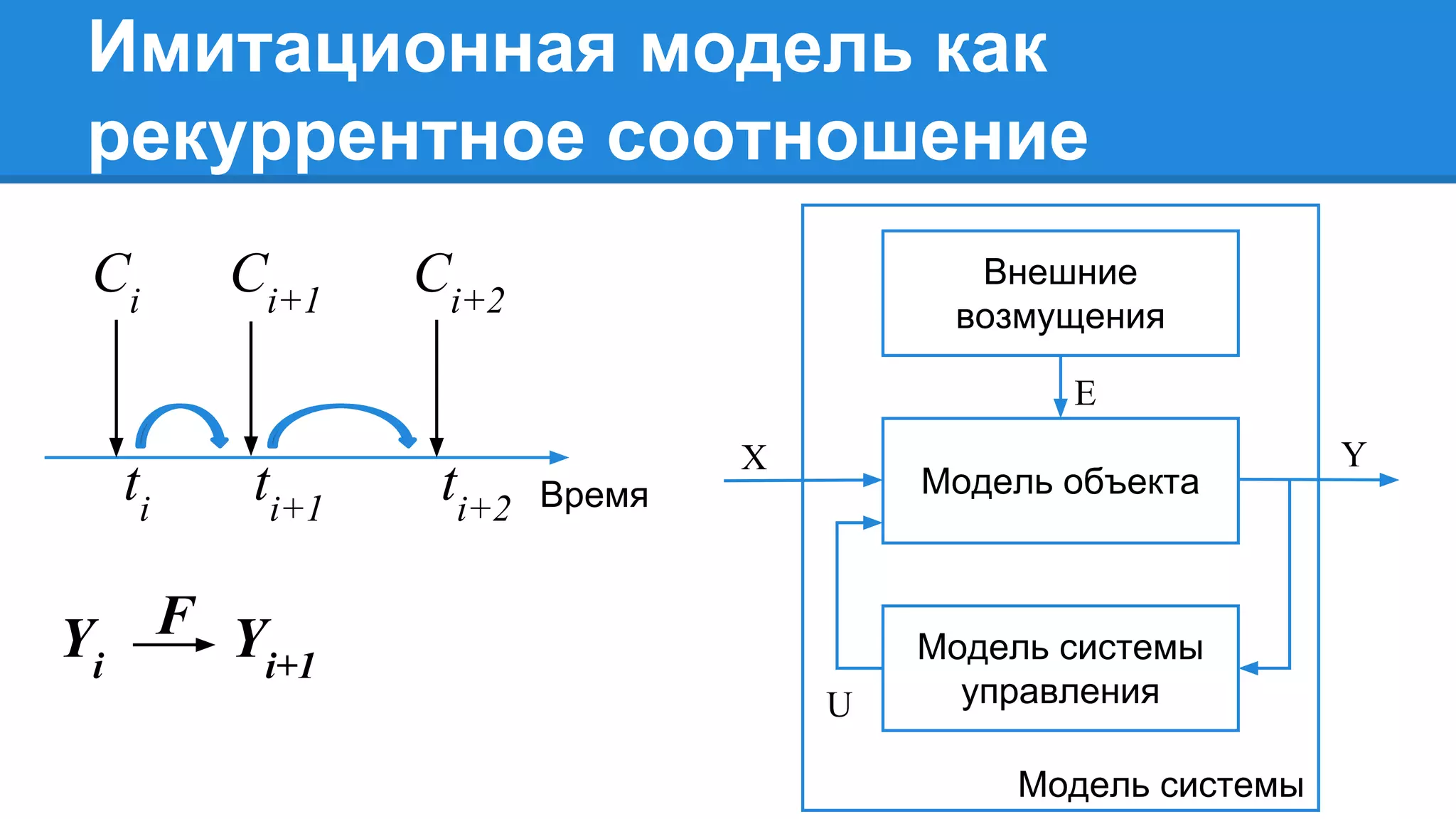
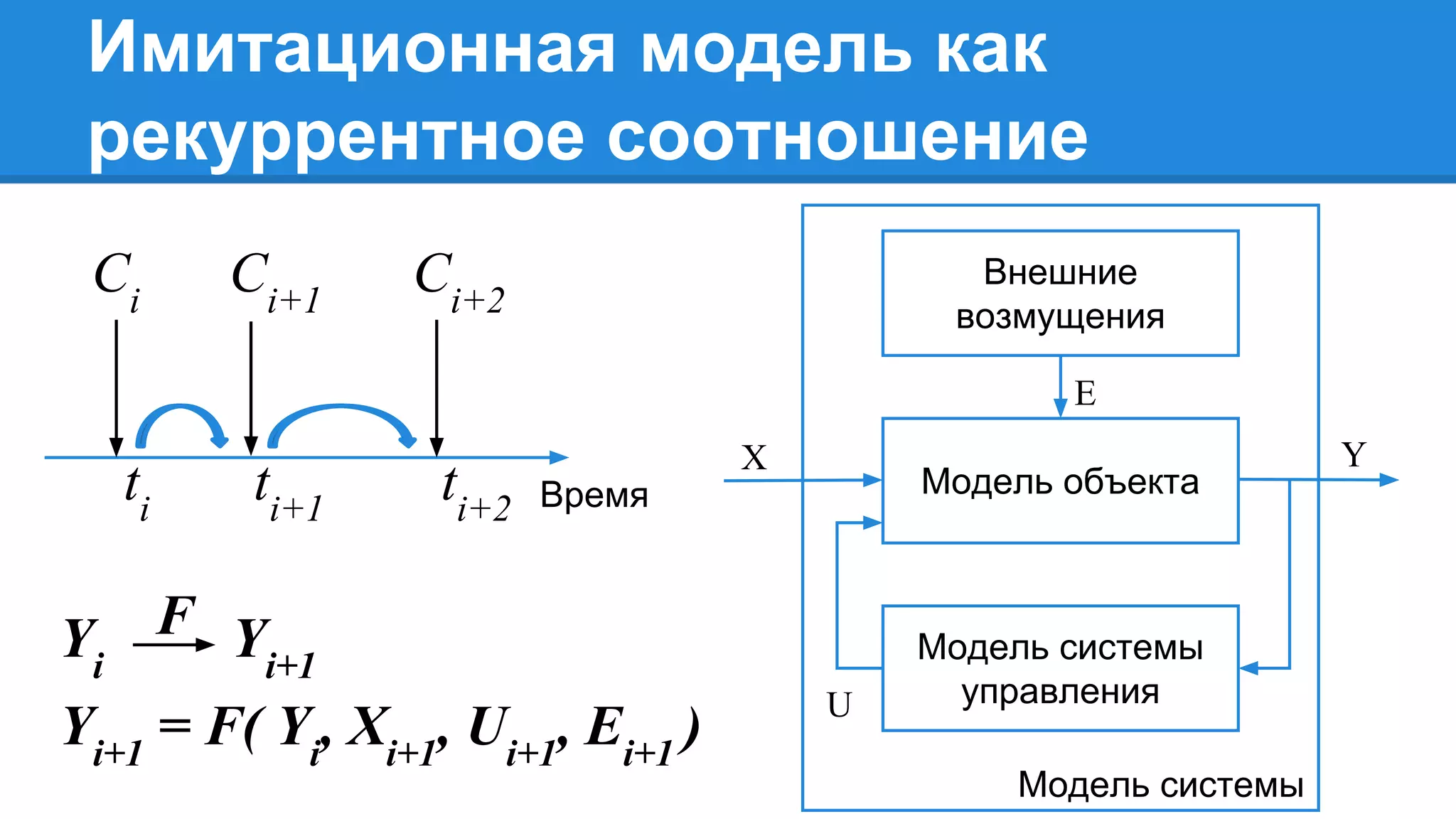
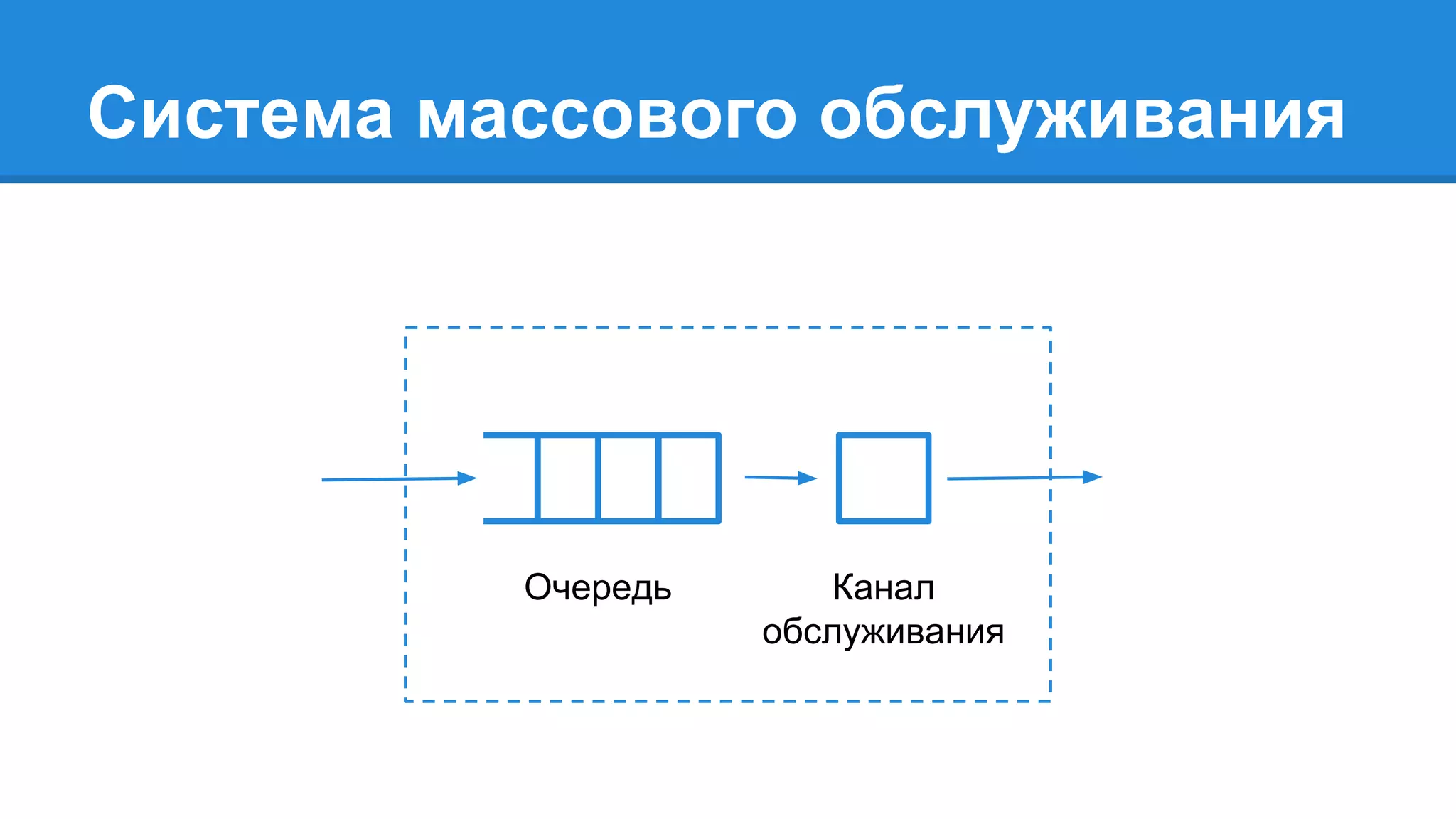
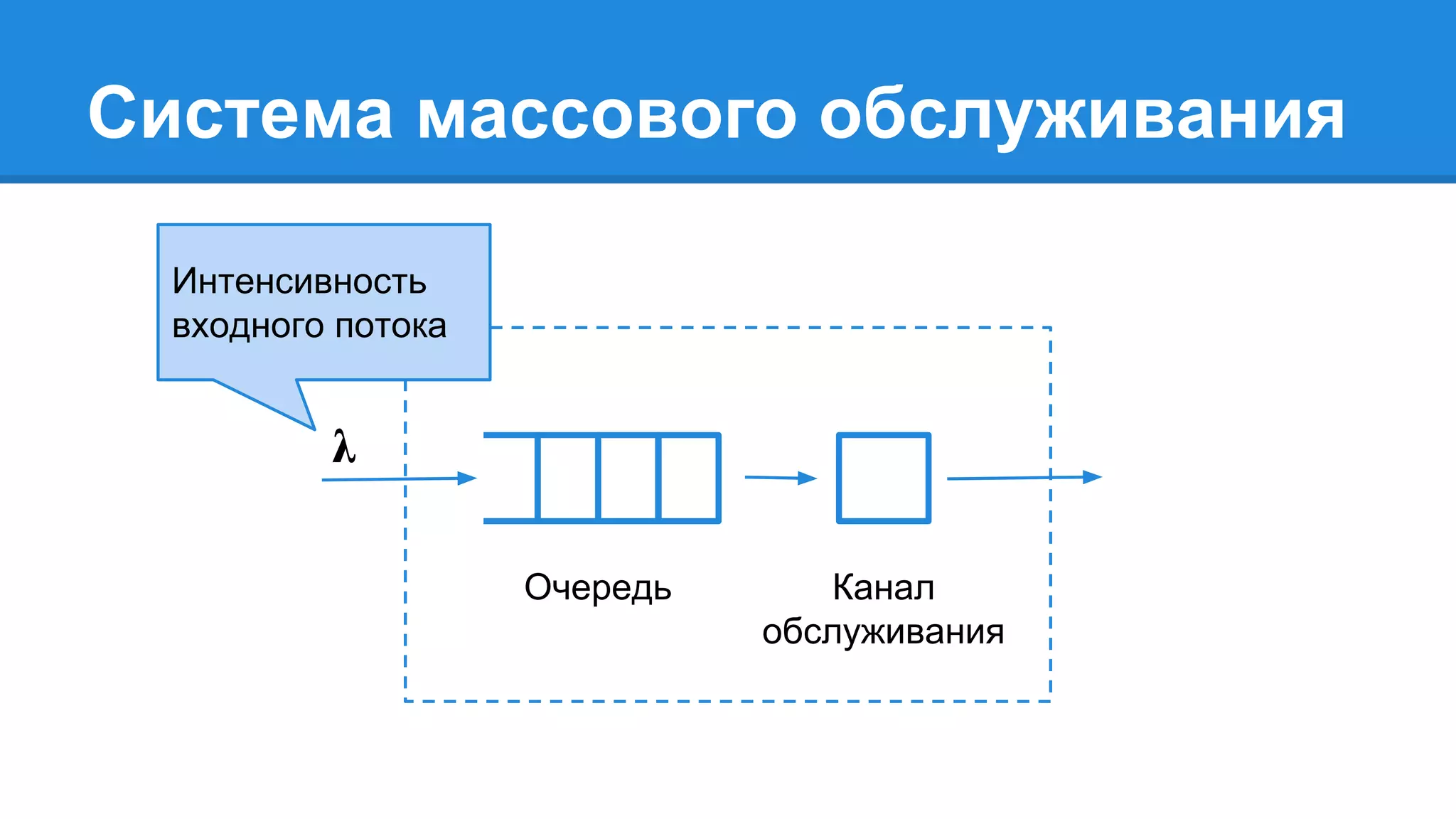
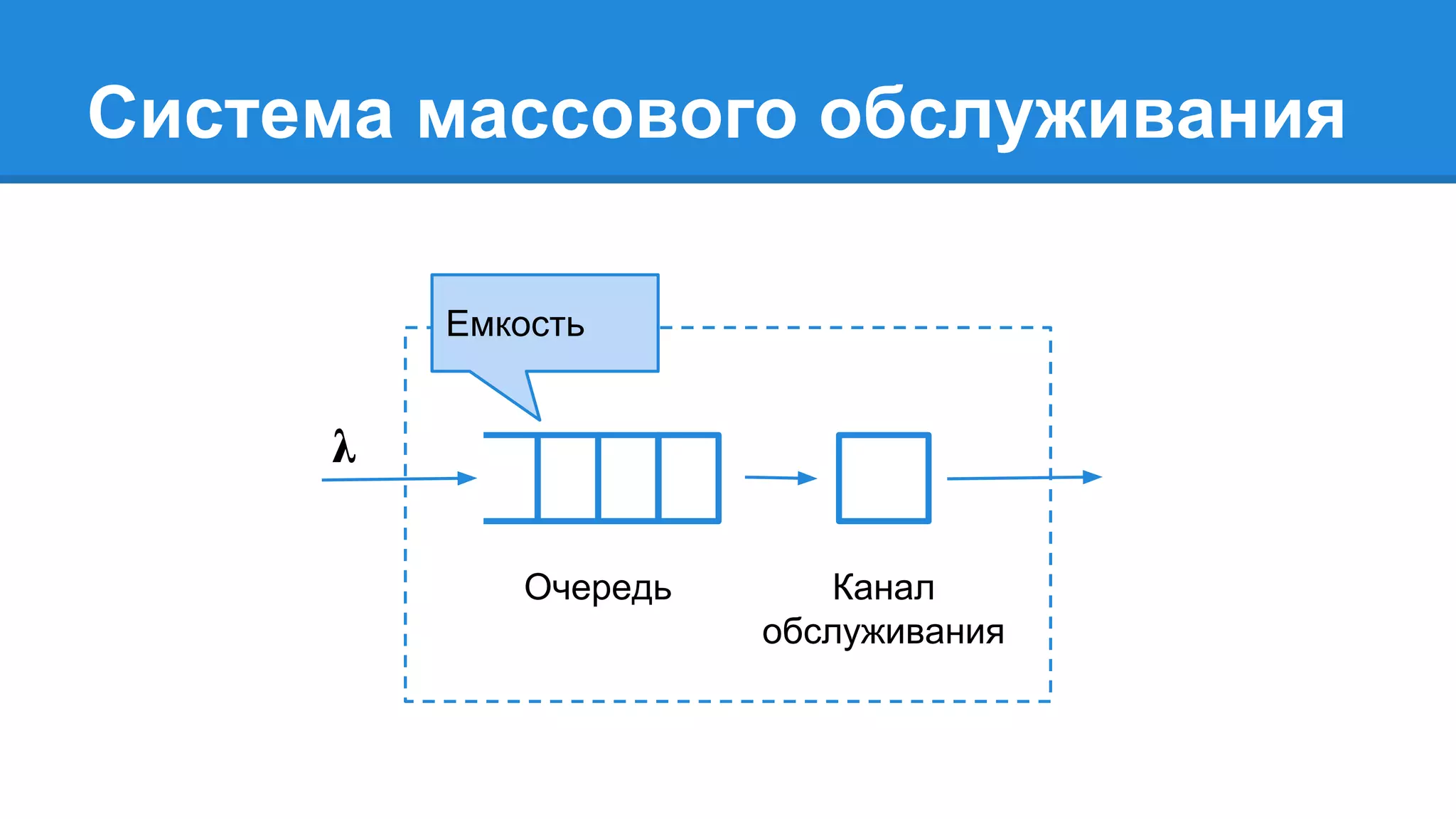
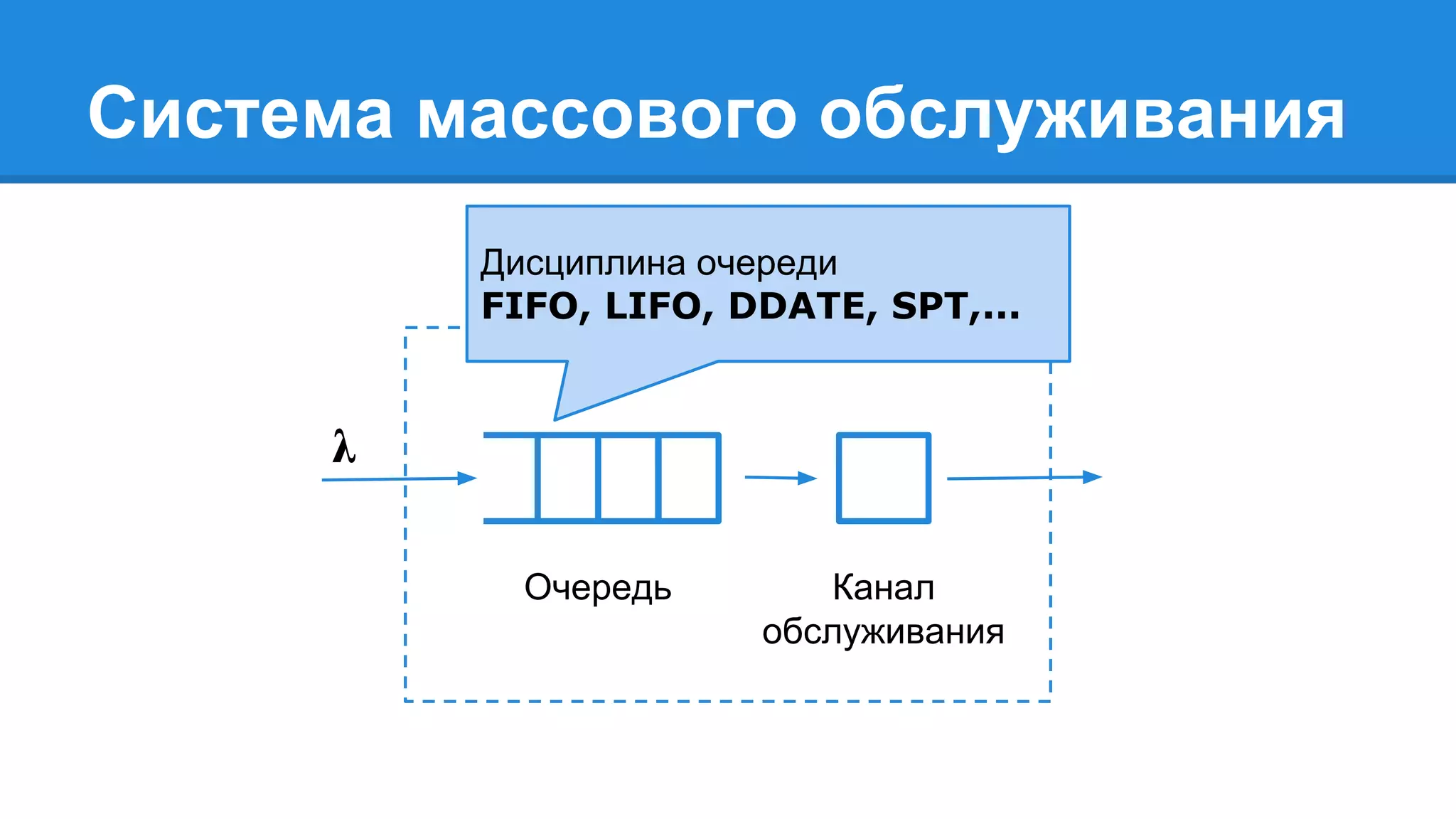
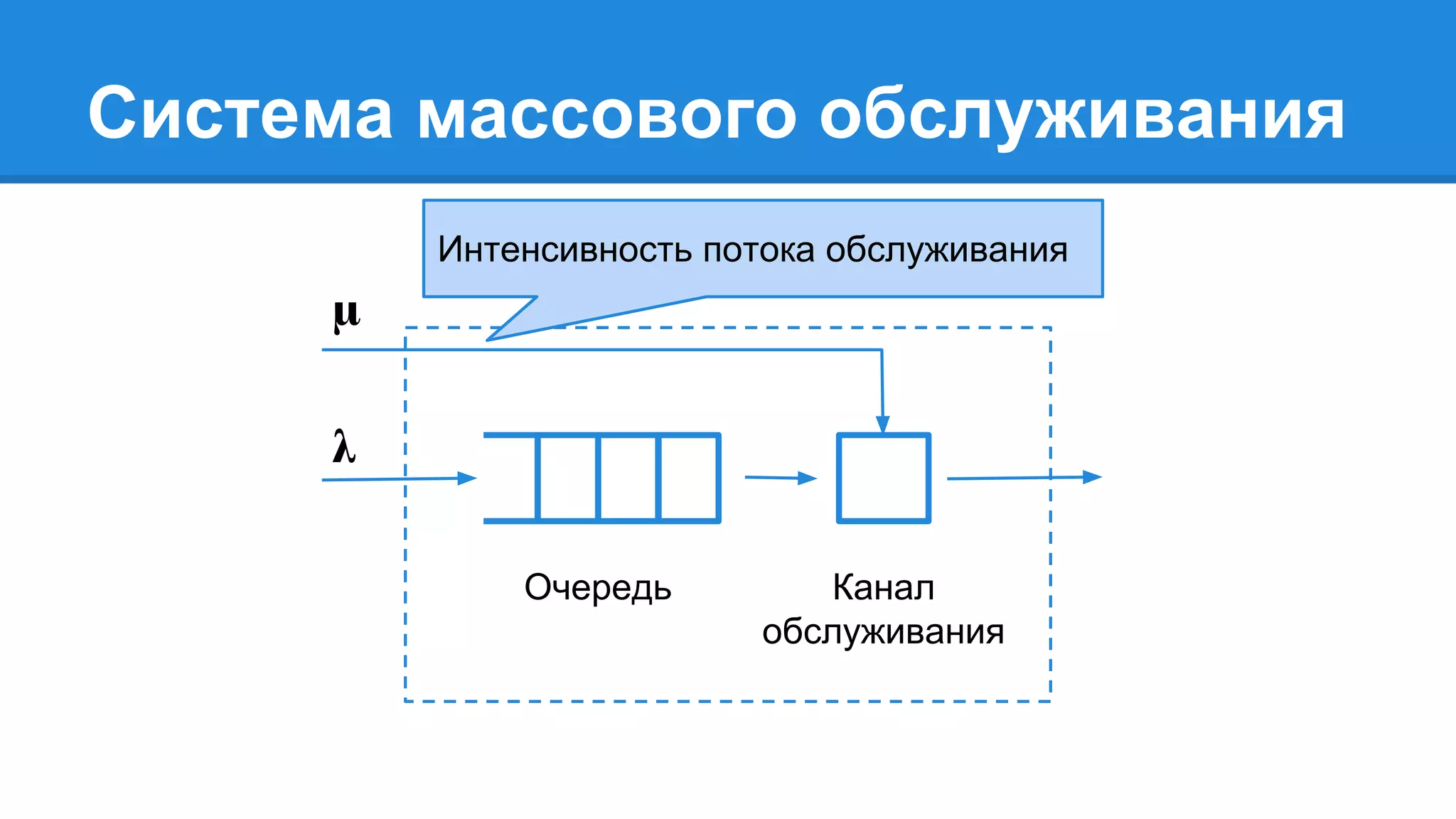
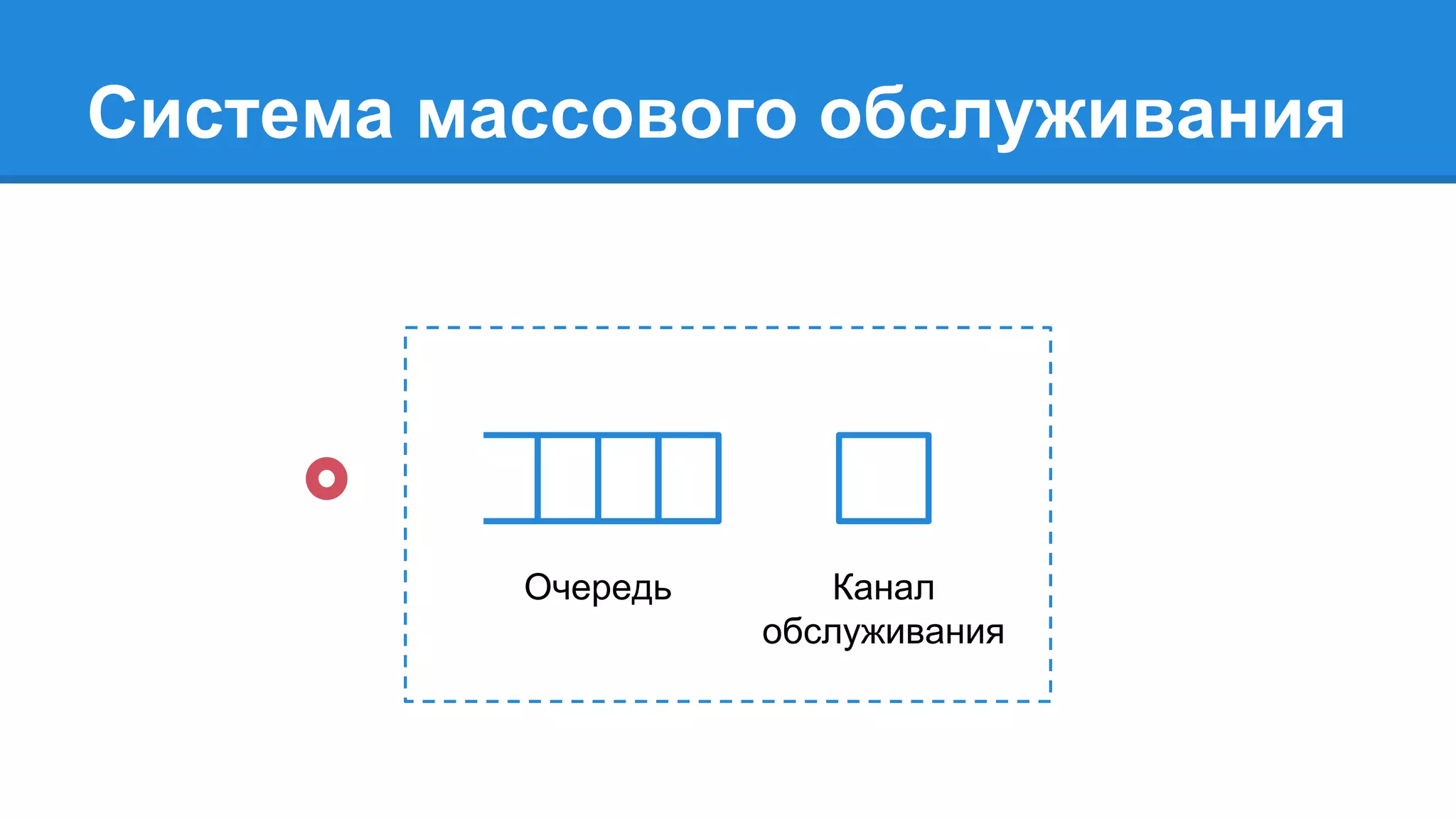
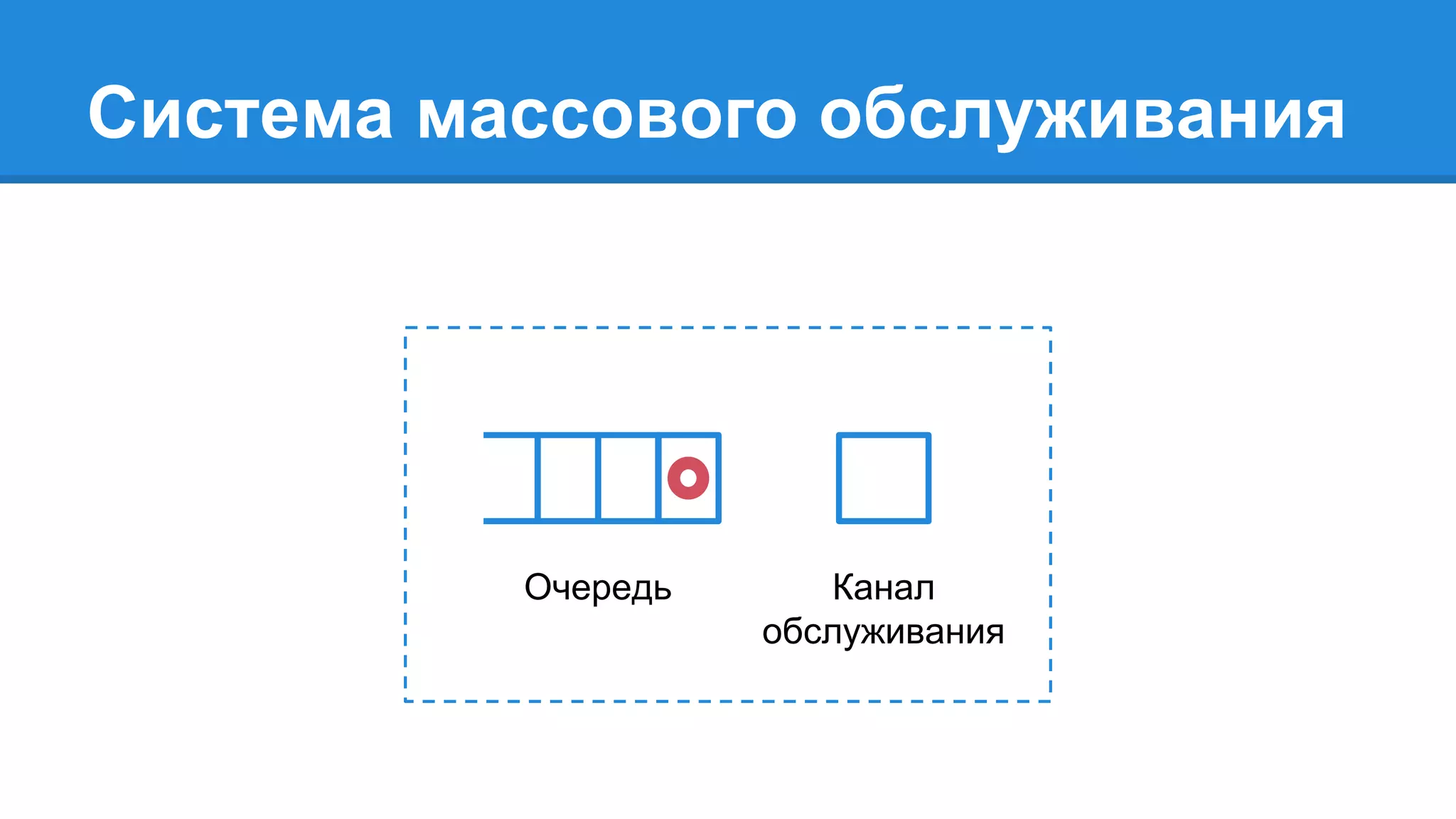
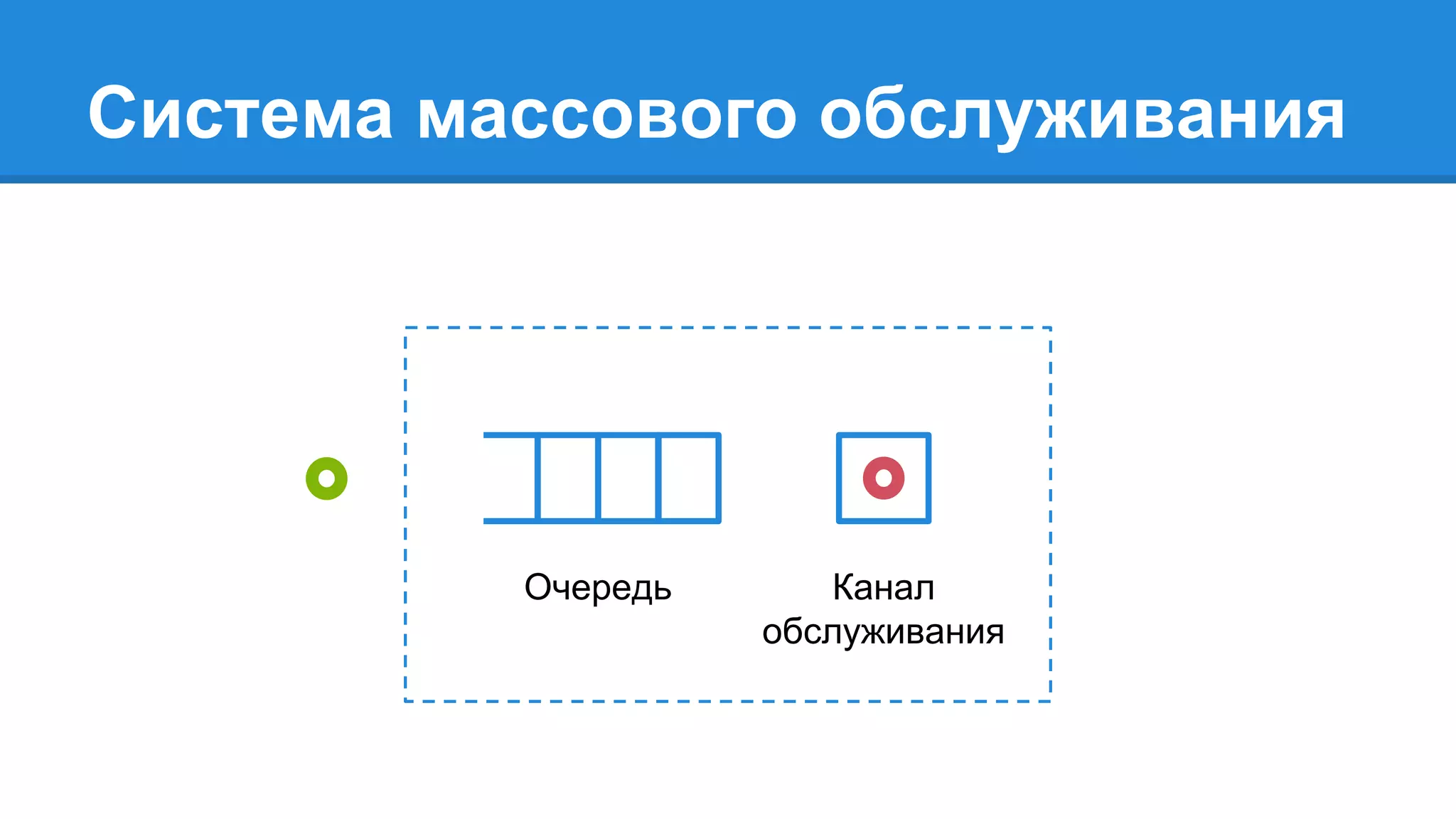
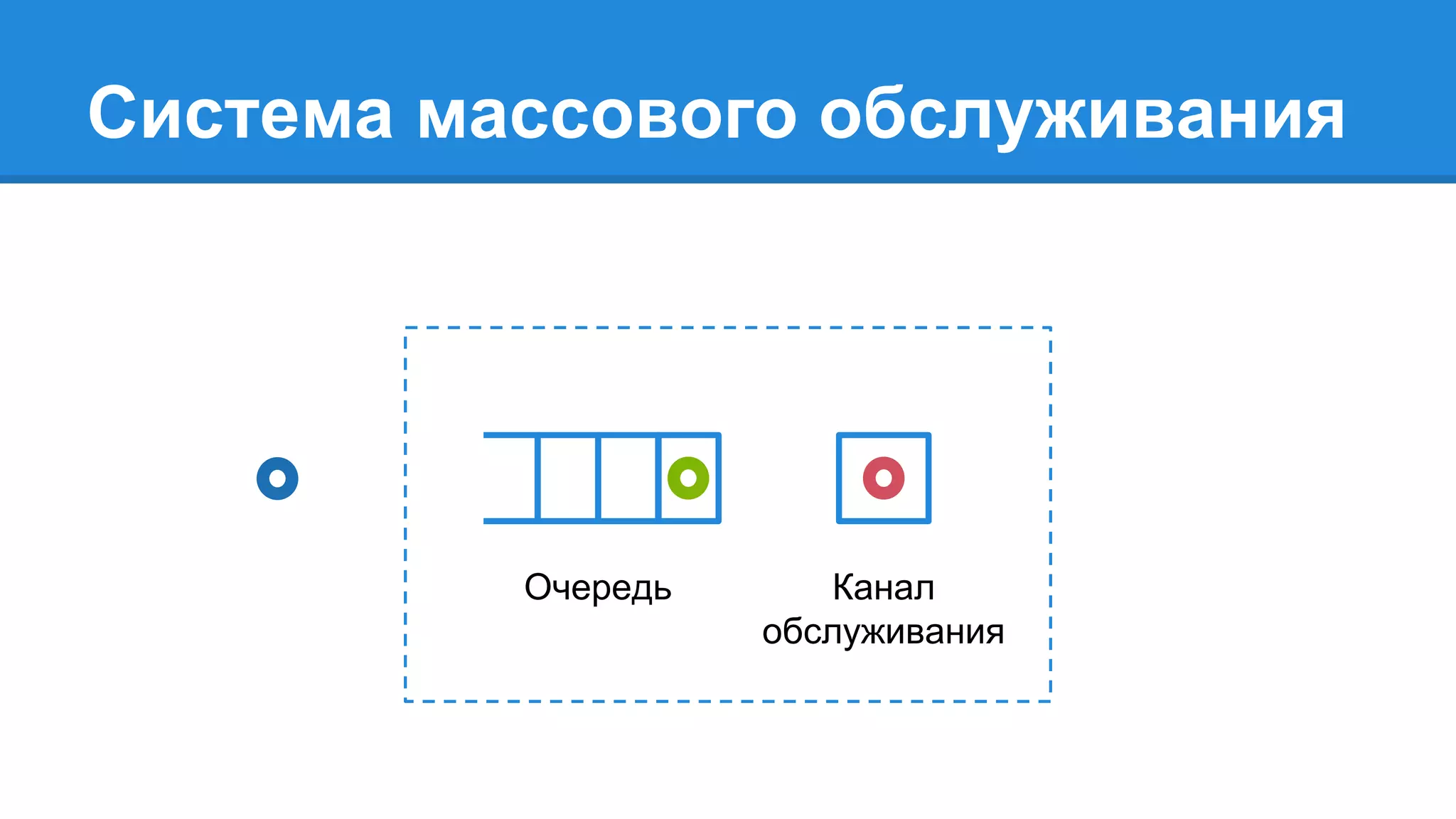
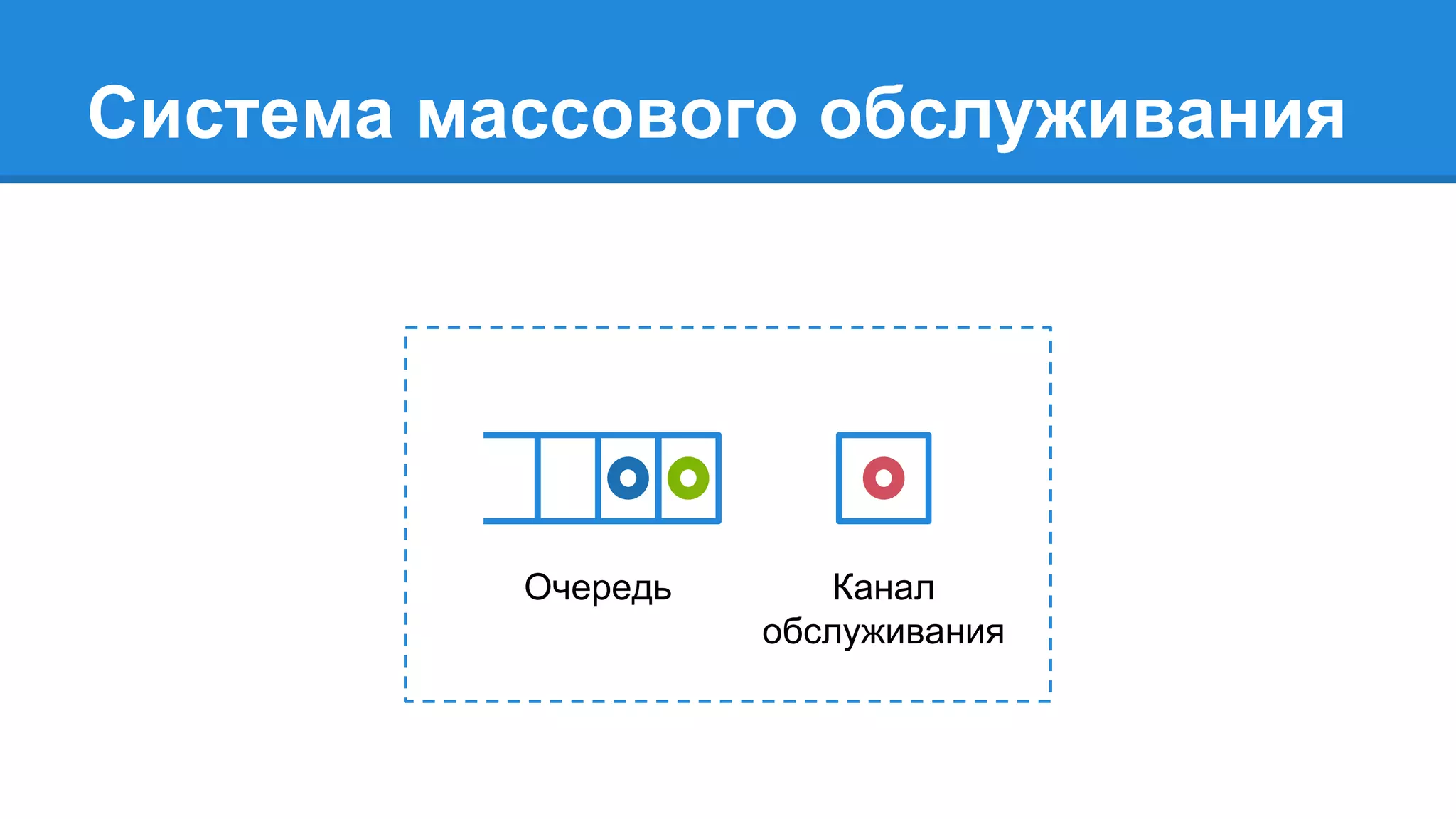
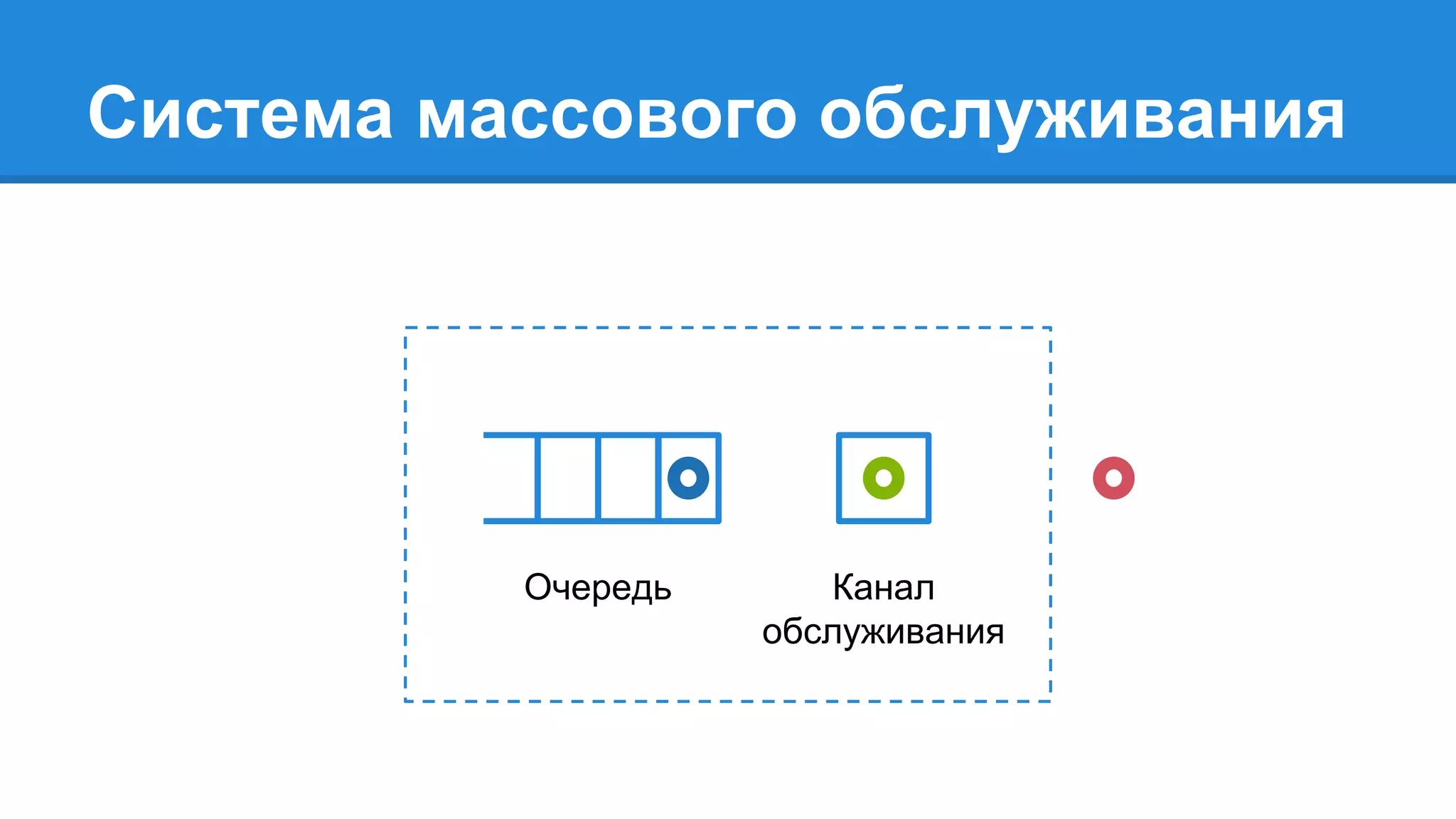
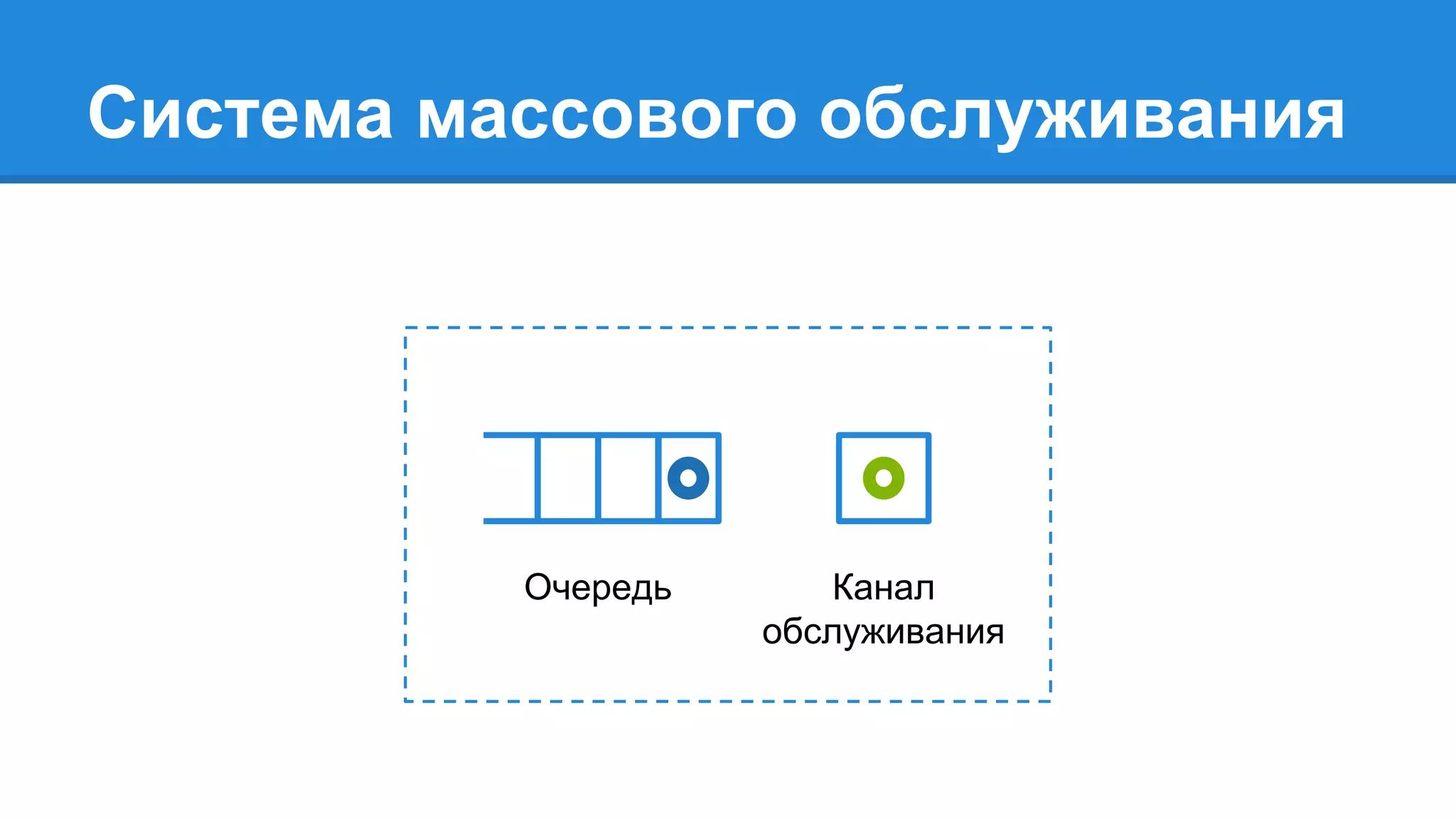
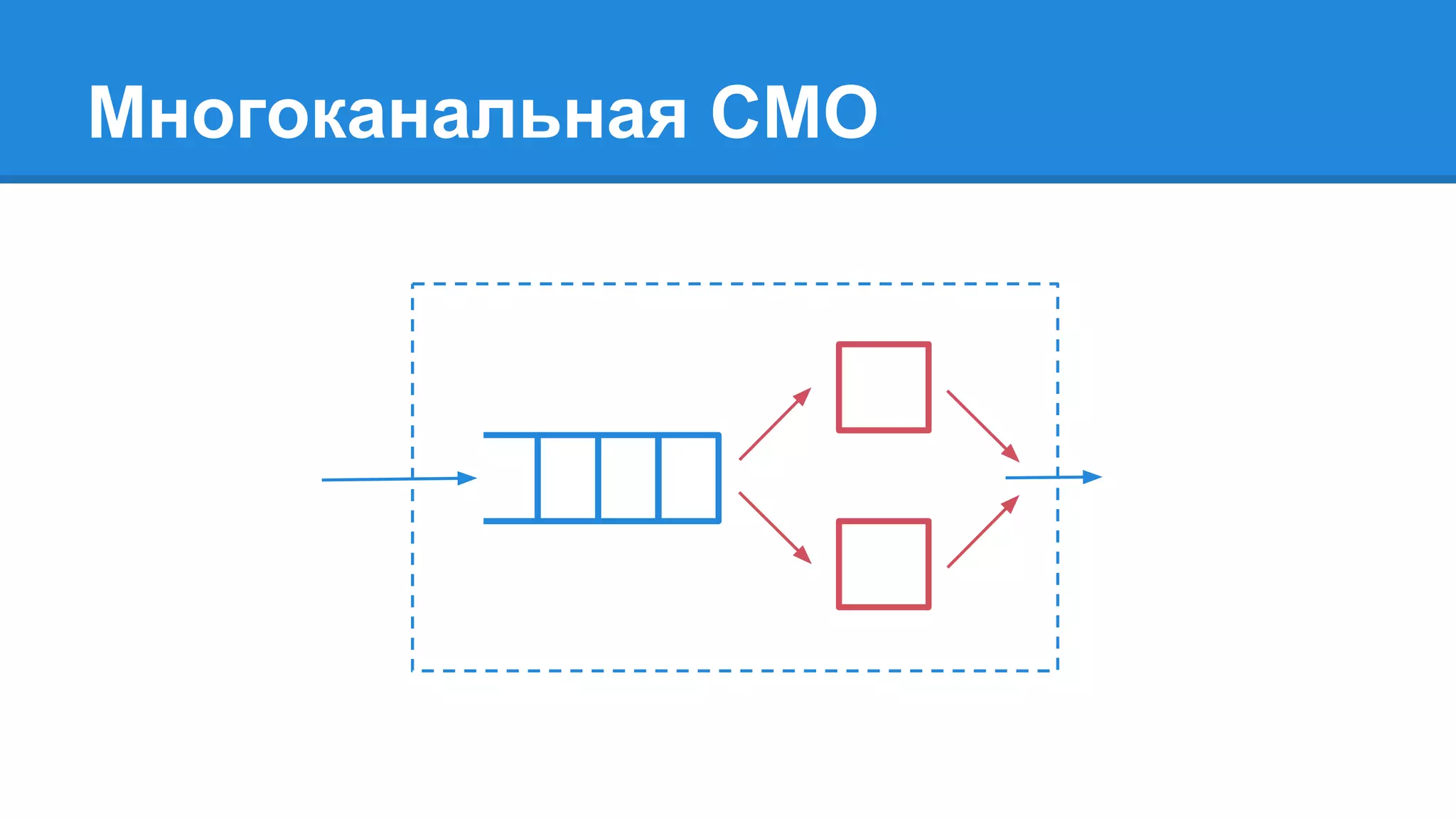
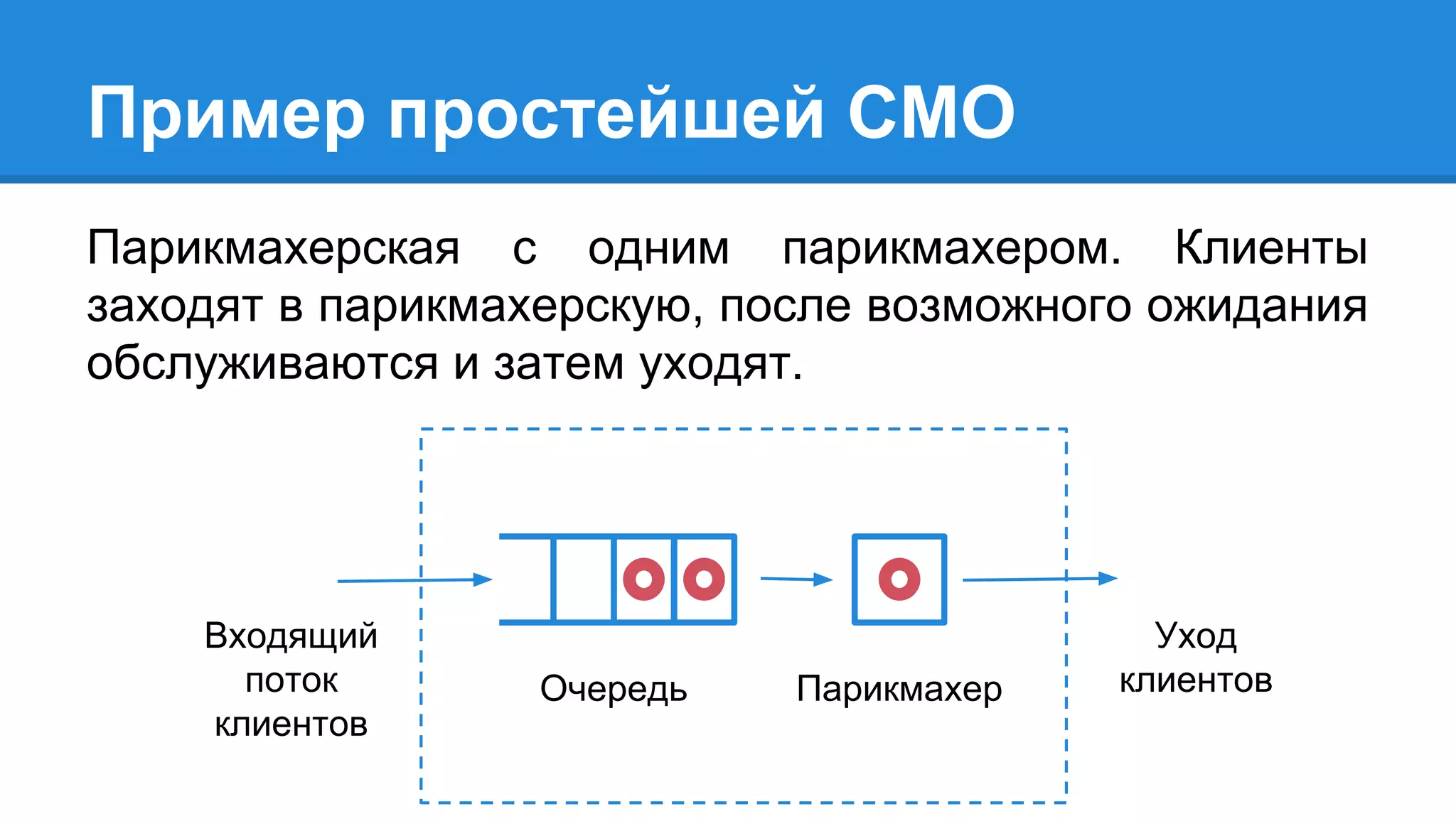
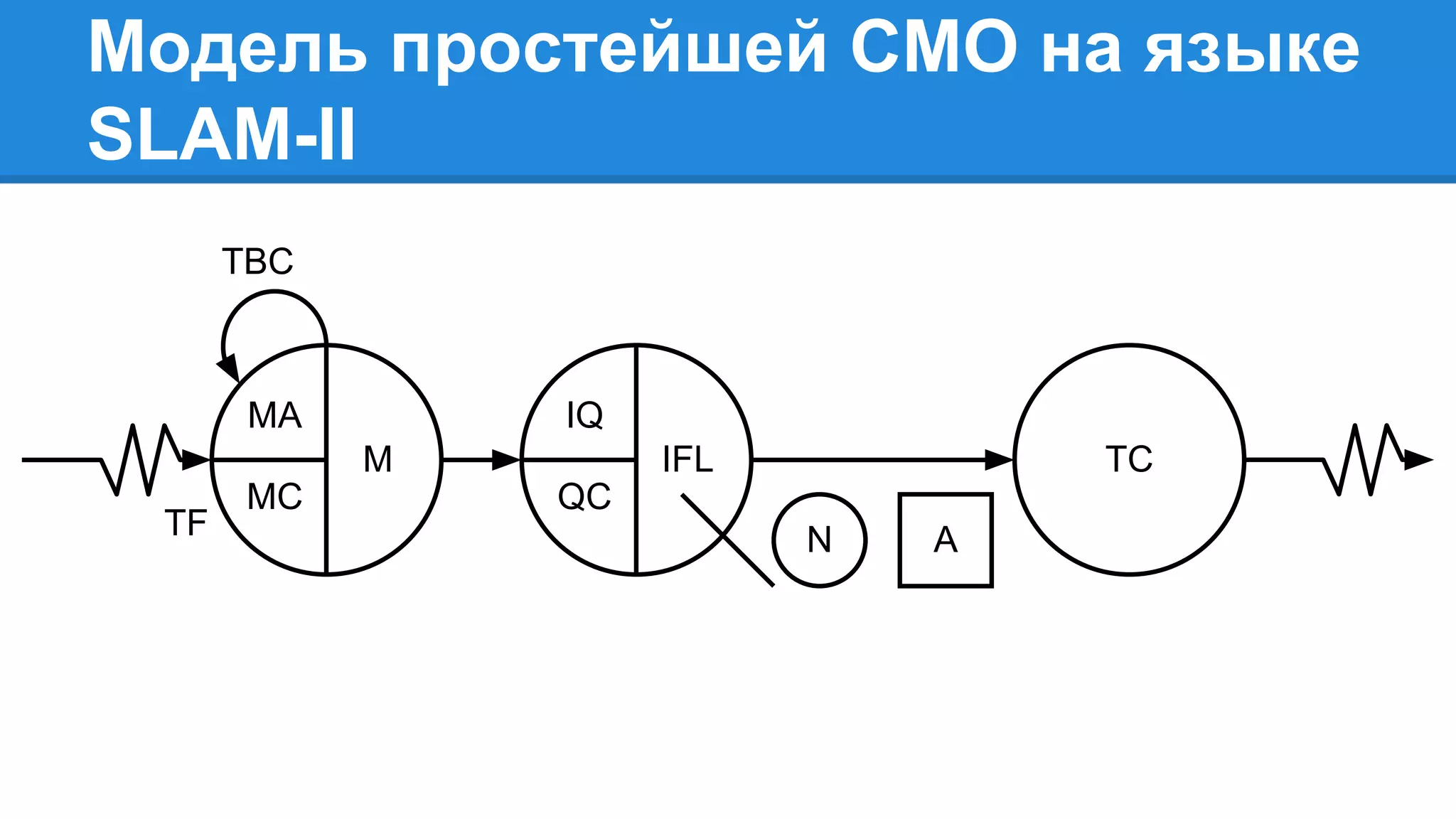
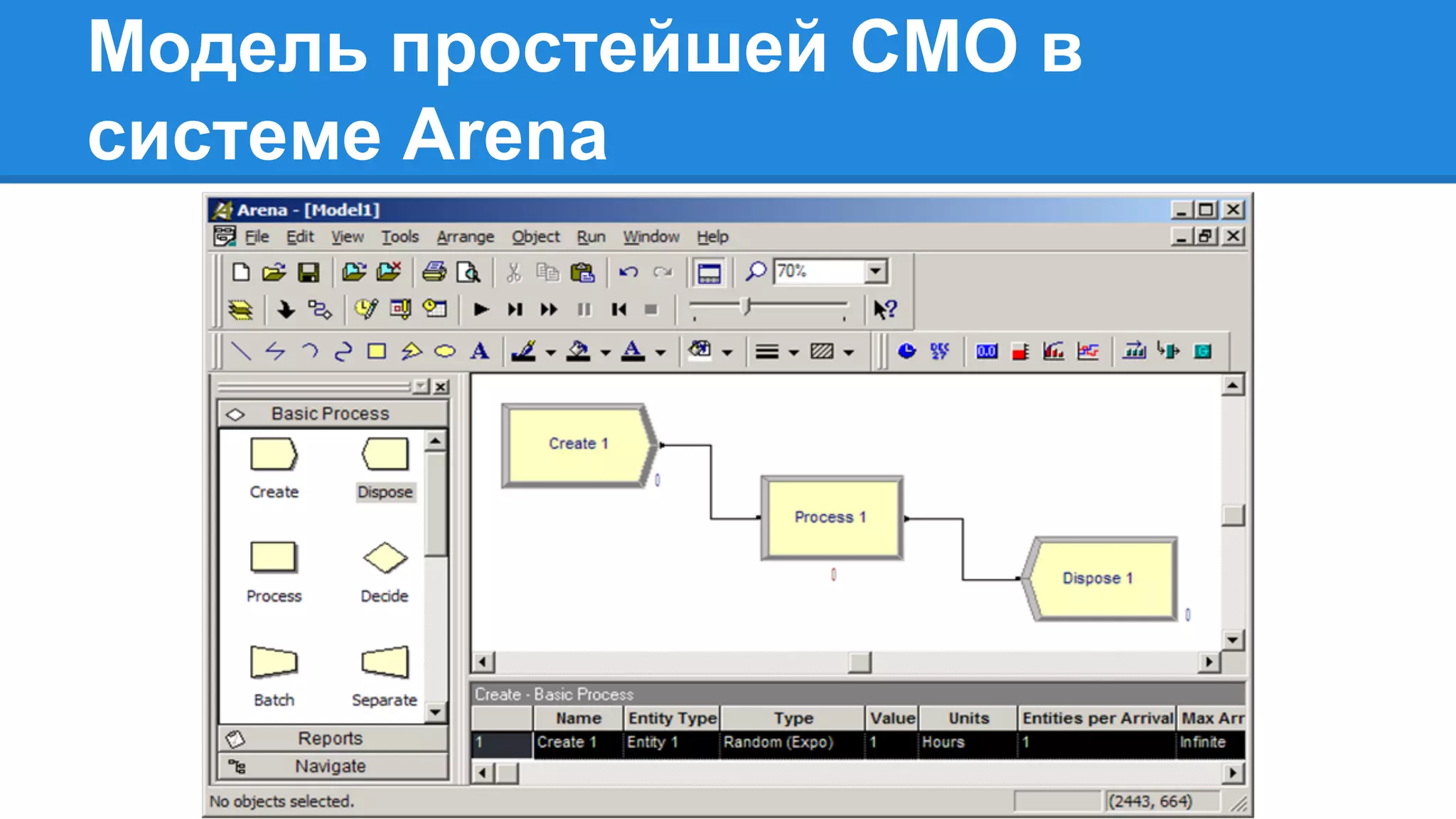
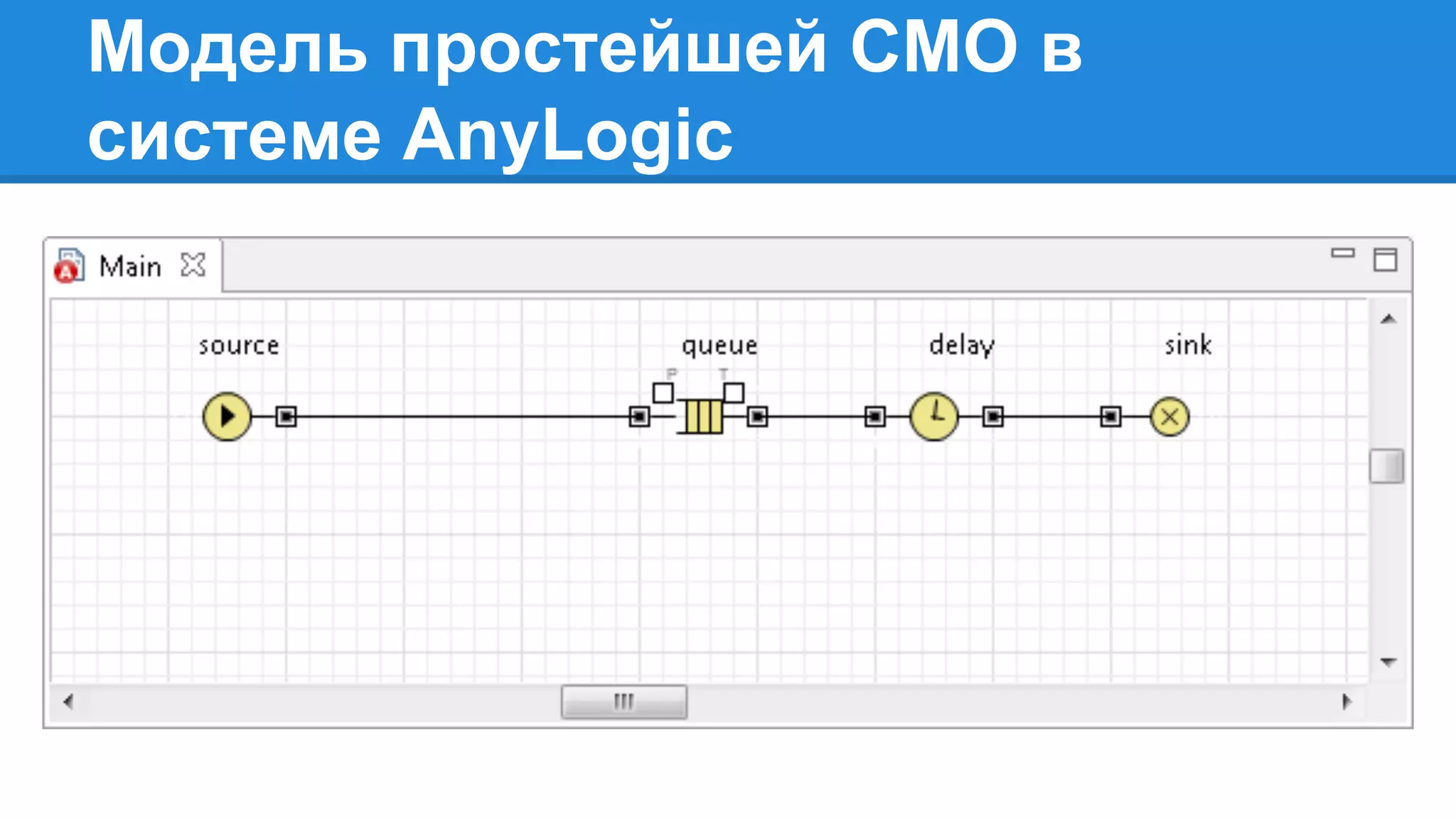
Документ описывает моделирование сложных дискретных систем, включая классификацию и характеристики имитационных моделей, а также подходы к их построению. Основное внимание уделяется системе массового обслуживания (СМО), подчеркивая важность математического моделирования для управления сложными системами и описания взаимодействия их компонентов. Также рассматриваются примеры реализации СМО и подходы к исследованию, такие как использование различных языков моделирования.
Моделирование ТПиПП
- 1.
- 2.
- 3. Система Система – этомножество взаимосвязанных объектов S = (O, R) O – множество объектов R – множество отношений
- 4. Внешнее и внутреннееописание системы СистемаX Y Внешняя среда
- 5. Внешнее и внутреннееописание системы СистемаX Y Внешняя среда Внешнее описание системы (система как “черный ящик”)X ➞ Y
- 6. Внешнее и внутреннееописание системы СистемаX Y Внешняя среда Внутреннее описание системы
- 7. Внешнее и внутреннееописание системы X Y Внешняя среда Объект1 Объект2 Объект3 Внутреннее описание системы
- 8. Внешнее и внутреннееописание системы X Y Внешняя среда Объект1 Объект2 Объект3 Внутреннее описание системы S = (O, R)
- 9.
- 10.
- 11. Метод декомпозиции Объект1 (подсистема) X11 X12 Y11 Внешняя среда Внешнееописание системы (система как “черный ящик”) Внутреннее описание системы
- 12. Дискретная система В дискретнойсистеме переменные состояния в различные моменты времени изменяются мгновенно
- 13.
- 14. Виды имитационного моделирования Дискретное НепрерывноеДискретно-непрерывное Время Переменная состояния Время Переменная состояния Время Переменные состояния
- 15. Сложная система Определения нет Носложная система имеет ряд признаков...
- 16. Признаки сложной системы Признакисложного объекта управления по Растригину Л.А. ● Сложным объектом нельзя управлять без его математической модели ● Стохастичность поведения ● “Нетерпимость” к управлению ● Нестационарность ● Невоспроизводимость экспериментов
- 17. Признаки сложной системы Основываясьна работе Саймона и Эндо, Куртуа предлагает следующее наблюдения ● Сложные системы представляются в виде иерархии ● Выбор низшего уровня абстракции произволен ● Работающая сложная система неизбежно оказывается результатом работающей простой системы
- 18. Признаки сложной системы Признакипо “здравому смыслу” ● Сложная система состоит из большого количества объектов ● Сложная система состоит из малого количества объектов, при большом многообразии их типов ● Тоже относится к связям ● Система сложна, если проектировщик не может “удержать” её в голове
- 19. Оценка сложности Согласно концепцииобщей теории систем сложность - это совокупность огромного числа различных объектов, функционирующих вместе и взаимодействующих непростым способом. Сложность есть взаимодействие и, более того, взаимозависимость, т.е. поведение одного или нескольких элементов воздействует на поведение других элементов. Сложность зависит не только от взаимозависимости, но и от числа взаимодействующих компонентов. Поэтому Р.Эшби оценивал степень сложности количеством информации, необходимой для описания реальной системы.
- 20.
- 21.
- 22. Типы сложности УправленияДинамическаяСтатическая Математическая структура объектов системы Способы связи объектов Поведение системы вовремени Объем вычислений для управления системой
- 23. Способы исследования системы Экспериментс реальной системой Эксперимент с моделью системы
- 24. Способы исследования системы Экспериментс реальной системой Эксперимент с моделью системы Физическая модель Математическая модель
- 25. Способы исследования системы Экспериментс реальной системой Эксперимент с моделью системы Физическая модель Математическая модель Аналитическое решение Имитационное моделирование
- 26. Способы исследования системы Экспериментс реальной системой Эксперимент с моделью системы Физическая модель Математическая модель Аналитическое решение Имитационное моделирование
- 27. Типы моделирующих отношений ТипПодлинная система Моделирующая система Пример Ⅰ Физическая Абстрактная Ⅱ Абстрактная Физическая Ⅲ Физическая Физическая Ⅳ Абстрактная Абстрактная
- 28. Типы моделирующих отношений ТипПодлинная система Моделирующая система Пример Ⅰ Физическая Абстрактная Все виды математических моделей, в том числе, имитационные модели Ⅱ Абстрактная Физическая Ⅲ Физическая Физическая Ⅳ Абстрактная Абстрактная
- 29. Типы моделирующих отношений ТипПодлинная система Моделирующая система Пример Ⅰ Физическая Абстрактная Все виды математических моделей, в том числе, имитационные модели Ⅱ Абстрактная Физическая Аналоговые компьютеры, электролитические ванны для решения уравнений в частных производных Ⅲ Физическая Физическая Ⅳ Абстрактная Абстрактная
- 30. Типы моделирующих отношений ТипПодлинная система Моделирующая система Пример Ⅰ Физическая Абстрактная Все виды математических моделей, в том числе, имитационные модели Ⅱ Абстрактная Физическая Аналоговые компьютеры, электролитические ванны для решения уравнений в частных производных Ⅲ Физическая Физическая Масштабные модели Ⅳ Абстрактная Абстрактная
- 31. Типы моделирующих отношений ТипПодлинная система Моделирующая система Пример Ⅰ Физическая Абстрактная Все виды математических моделей, в том числе, имитационные модели Ⅱ Абстрактная Физическая Аналоговые компьютеры, электролитические ванны для решения уравнений в частных производных Ⅲ Физическая Физическая Масштабные модели Ⅳ Абстрактная Абстрактная Модели для математических преобразований: Лапласа, Фурье и т.п.
- 32. Типы моделирующих отношений ТипПодлинная система Моделирующая система Пример Ⅰ Физическая Абстрактная Все виды математических моделей, в том числе, имитационные модели Ⅱ Абстрактная Физическая Аналоговые компьютеры, электролитические ванны для решения уравнений в частных производных Ⅲ Физическая Физическая Масштабные модели Ⅳ Абстрактная Абстрактная Модели для математических преобразований: Лапласа, Фурье и т.п.
- 33. Классификация имитационных моделей Нужен лиучет времени ? Статическая Динамическая
- 34. Классификация имитационных моделей Нужен лиучет времени ? Есть ли случайные возмущения ? Статическая Динамическая Детерминированная Стохастическая
- 35. Классификация имитационных моделей Нужен лиучет времени ? Есть ли случайные возмущения ? Плавное изменение переменных ? Статическая Динамическая Детерминированная Стохастическая Непрерывная Дискретная
- 36. Классификация имитационных моделей Нужен лиучет времени ? Есть ли случайные возмущения ? Плавное изменение переменных ? Статическая Динамическая Детерминированная Стохастическая Непрерывная Дискретная
- 37. Подходы к построению имитационныхмоделей Дискретные Событийный подход Подход сканирования активностей Процессно- ориентированный подход
- 38. Подходы к построению имитационныхмоделей Дискретные Непрерывные Событийный подход Подход сканирования активностей Процессно- ориентированный подход Дифференциальные уравнения первого порядка с начальными условиями Разностные уравнения
- 39. Подходы к построению имитационныхмоделей Дискретные Непрерывные Событийный подход Подход сканирования активностей Процессно- ориентированный подход Дифференциальные уравнения первого порядка с начальными условиями Разностные уравнения
- 40.
- 41. Дискретное имитационное моделирование Под дискретнойимитационной моделью понимают такую модель, состояние которой изменяется в определенные моменты времени t1 ,t2 ,…,ti ,…,tn . На интервале времени [ti ,ti+1 ) переменные не изменяются, и их значения равны значениям в момент времени ti .
- 42.
- 43. Y U E Модель системы Модель системы управления Модельобъекта Внешние возмущения X Имитационная модель как рекуррентное соотношение Время Ci Ci+1 Ci+2 ti ti+1 ti+2
- 44. Y U E Модель системы Модель системы управления Модельобъекта Внешние возмущения X Yi Yi+1 F Имитационная модель как рекуррентное соотношение Время Ci Ci+1 Ci+2 ti ti+1 ti+2
- 45. Y U E Модель системы Модель системы управления Модельобъекта Внешние возмущения X Yi Yi+1 F Yi+1 = F( Yi , Xi+1 , Ui+1 , Ei+1 ) Имитационная модель как рекуррентное соотношение Время Ci Ci+1 Ci+2 ti ti+1 ti+2
- 46.
- 47. Процессно-ориентированный подход ● Используется длямоделирования систем массового обслуживания (СМО) ● Имитационная модель содержит последовательность операторов, описывающих процесс обслуживания ● Язык моделирования преобразует такие операторы в последовательность событий
- 48. Система массового обслуживания ОчередьКанал обслуживания
- 49. Система массового обслуживания ОчередьКанал обслуживания Интенсивность входного потока
- 50. Система массового обслуживания ОчередьКанал обслуживания Емкость
- 51. Система массового обслуживания ОчередьКанал обслуживания Дисциплина очереди FIFO, LIFO, DDATE, SPT,...
- 52. Система массового обслуживания ОчередьКанал обслуживания Интенсивность потока обслуживания
- 53. Система массового обслуживания ОчередьКанал обслуживания
- 54. Система массового обслуживания ОчередьКанал обслуживания
- 55. Система массового обслуживания ОчередьКанал обслуживания
- 56. Система массового обслуживания ОчередьКанал обслуживания
- 57. Система массового обслуживания ОчередьКанал обслуживания
- 58. Система массового обслуживания ОчередьКанал обслуживания
- 59. Система массового обслуживания ОчередьКанал обслуживания
- 60.
- 61.
- 62. Пример простейшей СМО Парикмахерскаяс одним парикмахером. Клиенты заходят в парикмахерскую, после возможного ожидания обслуживаются и затем уходят. Очередь Парикмахер Входящий поток клиентов Уход клиентов
- 63. TBC TF MA MC M TC IQ QC N A IFL Модельпростейшей СМО на языке SLAM-II
- 64. Модель простейшей СМОв системе Arena
- 65. Модель простейшей СМОв системе AnyLogic
- 66. Язык GPSS General PurposeSimulation System
- 67. Модель простейшей СМОв операторной форме СОЗДАВАТЬ прибывающих Клиентов через каждые Т единиц времени ОЖИДАТЬ Парикмахера ПРОДВИНУТЬ модельное время на Продолжительность обслуживания ОСВОБОДИТЬ Парикмахера УДАЛИТЬ Клиента
- 68. Модель простейшей СМОв операторной форме СОЗДАВАТЬ прибывающих Клиентов через каждые Т единиц времени ОЖИДАТЬ Парикмахера ПРОДВИНУТЬ модельное время на Продолжительность обслуживания ОСВОБОДИТЬ Парикмахера УДАЛИТЬ Клиента
- 69. Модель простейшей СМОв операторной форме СОЗДАВАТЬ прибывающих Клиентов через каждые Т единиц времени ОЖИДАТЬ Парикмахера ПРОДВИНУТЬ модельное время на Продолжительность обслуживания ОСВОБОДИТЬ Парикмахера УДАЛИТЬ Клиента
- 70. Пример системы массового обслуживания- парикмахерская ● Интервал между прибытиями - равномерно распределенное случайное число от 12 до 24 минут включительно ● Время обслуживания - равномерно распределенное случайное число от 10 до 20 минут включительно ● Длина очереди не ограничена ● В начале система пуста ● Время завершения работы - смена - 480 минут ● Дисциплина очереди - FIFO ● Собираемые показатели - типичные для СМО
- 71. GENERATE SEIZE ADVANCE RELEASE TERMINATE 18,6 BARBER 15,5 BARBER ; Приход Клиента ;Переход к Парикмахеру ; Обслуживание ; Освобождение Парикмахера ; Уход Клиента Модель простейшей СМО на языке GPSS
- 72. GENERATE SEIZE ADVANCE RELEASE TERMINATE 18,6 BARBER 15,5 BARBER ; Приход Клиента ;Переход к Парикмахеру ; Обслуживание ; Освобождение Парикмахера ; Уход Клиента Модель простейшей СМО на языке GPSS GENERATE TERMINATE 480 1 ; Конец смены ; Окончание моделирования
- 73. GENERATE SEIZE ADVANCE RELEASE TERMINATE 18,6 BARBER 15,5 BARBER ; Приход Клиента ;Переход к Парикмахеру ; Обслуживание ; Освобождение Парикмахера ; Уход Клиента Модель простейшей СМО на языке GPSS
- 74. Модель простейшей СМОна языке GPSS GENERATE QUEUE SEIZE DEPART ADVANCE RELEASE TERMINATE 18,6 QUEUE1 BARBER QUEUE1 15,5 BARBER ; Приход Клиента ; Появление в очереди ; Переход к Парикмахеру ; Уход из очереди ; Обслуживание ; Освобождение Парикмахера ; Уход Клиента
- 75. Модель простейшей СМОна языке GPSS GENERATE QUEUE QUEUE SEIZE DEPART ADVANCE RELEASE DEPART TERMINATE 18,6 QUEUE2 QUEUE1 BARBER QUEUE1 15,5 BARBER QUEUE2 ; Приход Клиента ; Появление в системе ; Появление в очереди ; Переход к Парикмахеру ; Уход из очереди ; Обслуживание ; Освобождение Парикмахера ; Уход из системы ; Уход Клиента
- 76. Список литературы Томашевский В.Н., ЖдановаЕ.Г. Имитационное моделирование в среде GPSS. - "Бестселлер", 2003. - 416 с.
- 77. Список литературы Прицкер А. Введениев имитационное моделирование и язык СЛАМ II. –М.: Мир, 1987.
- 78.
- 79.