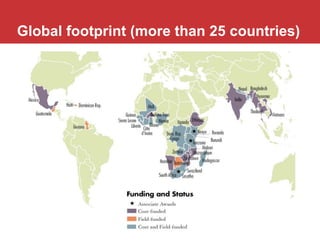
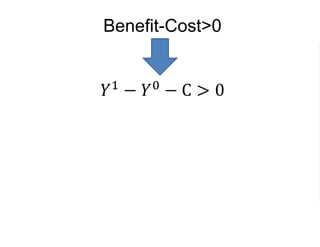
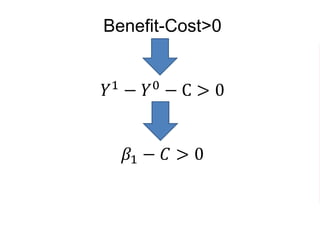
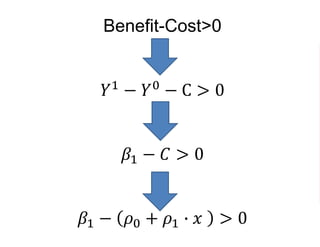
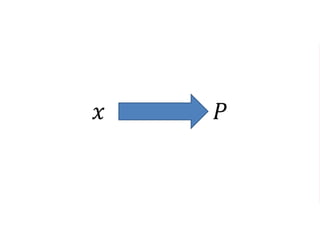
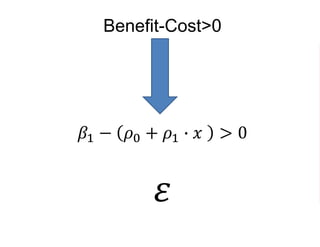
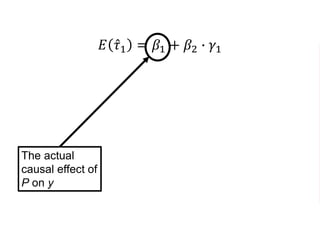
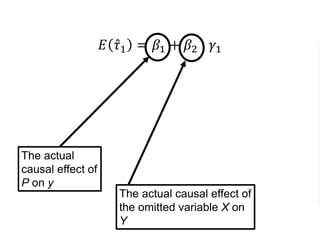
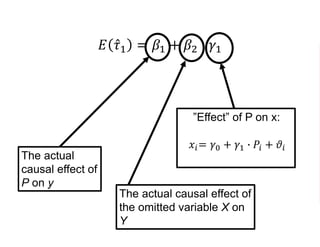
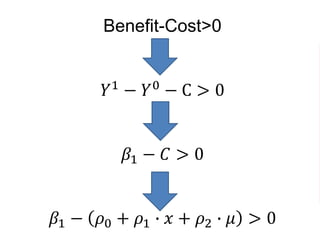
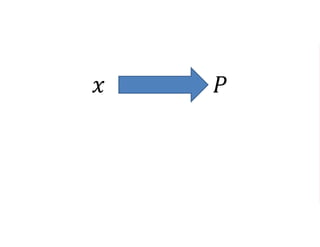
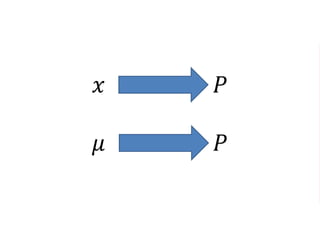
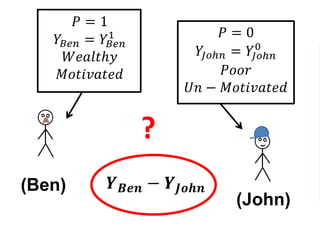
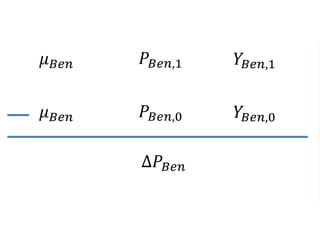
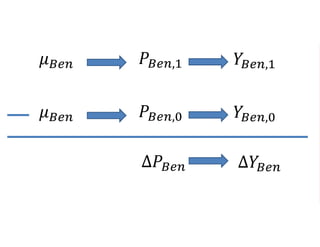
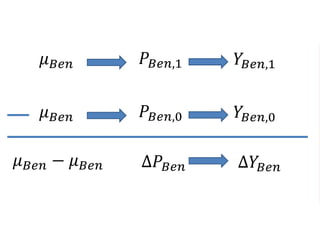
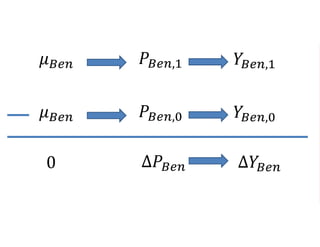
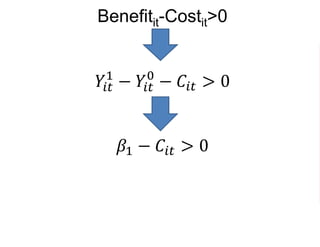
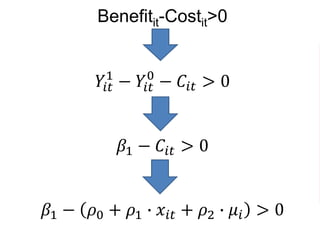
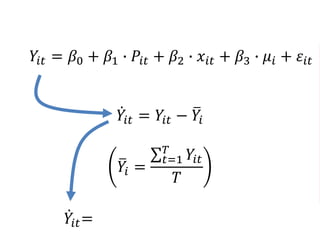
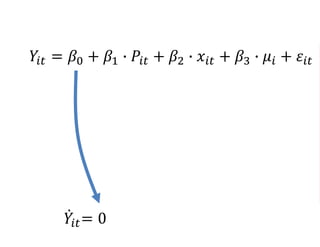
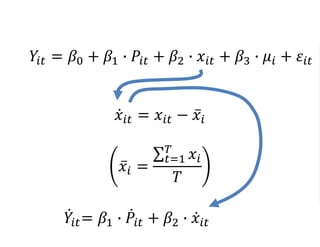
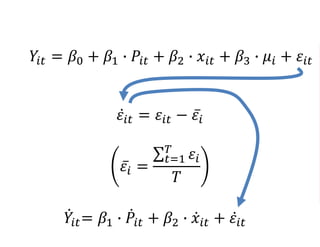
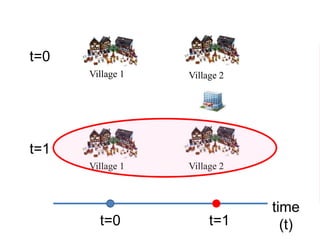
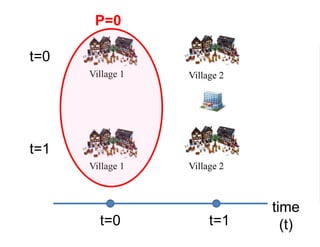
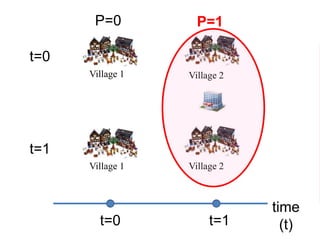
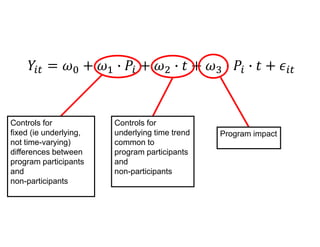
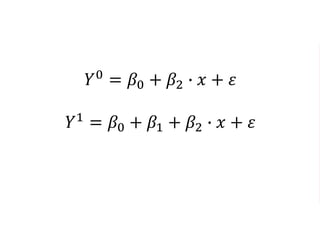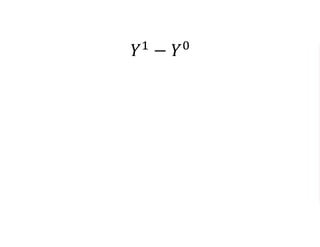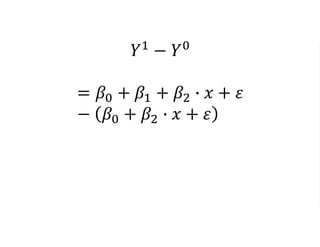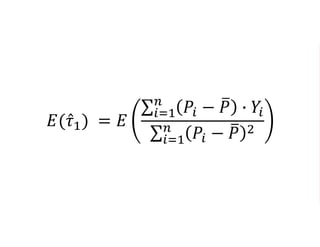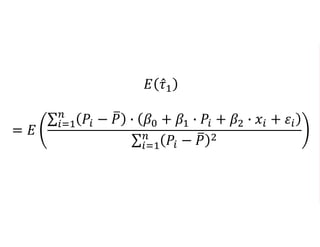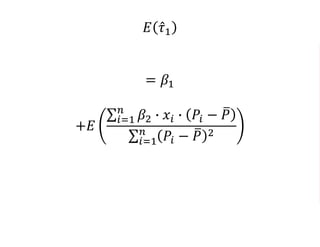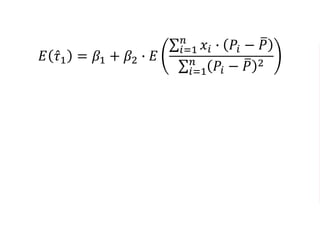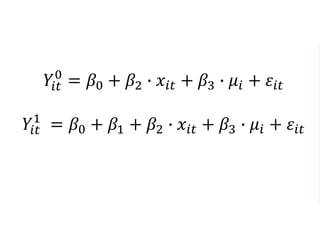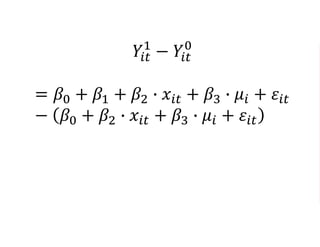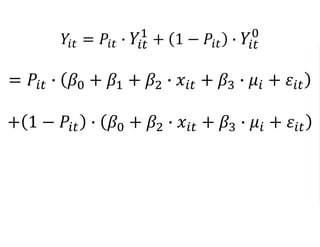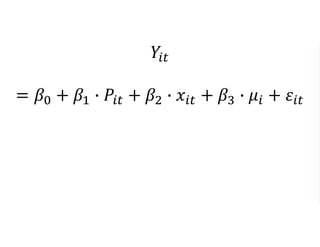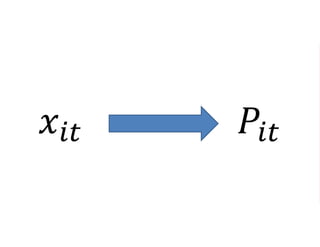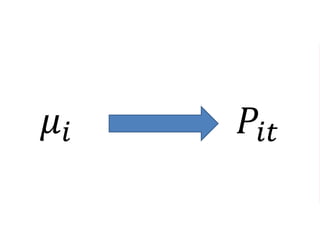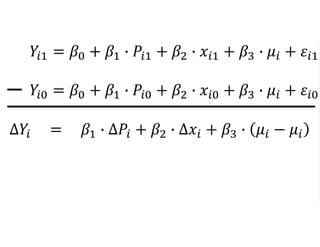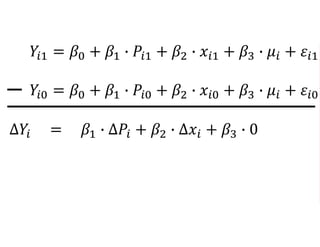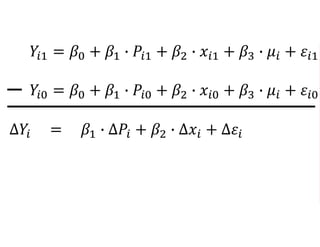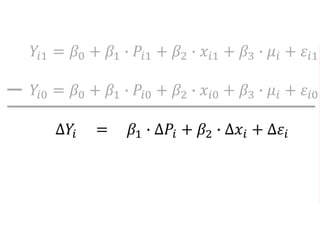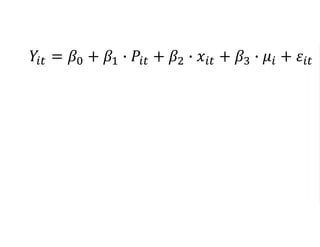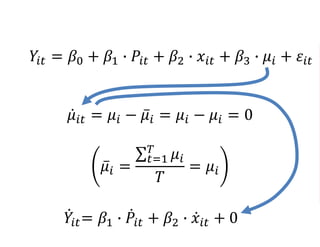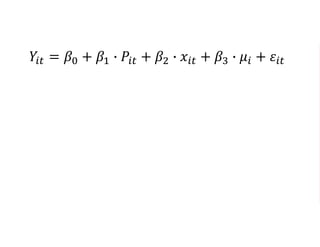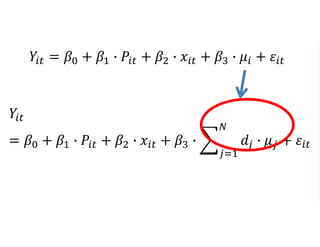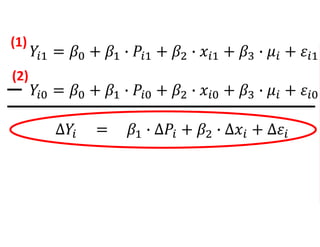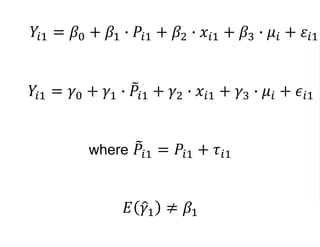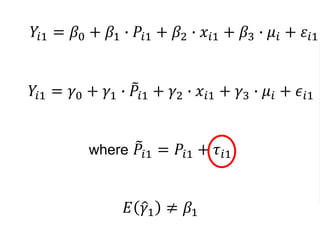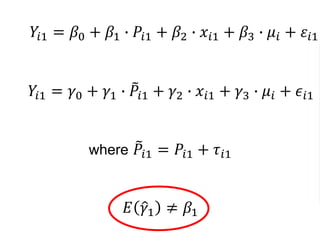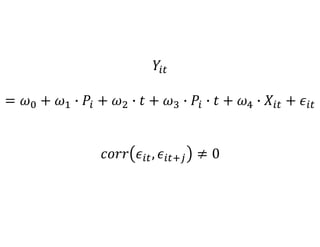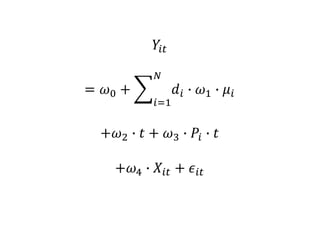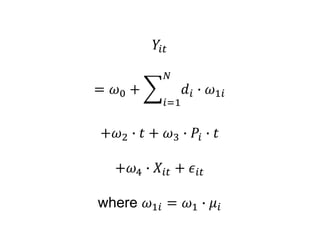The document outlines a five-year, $180 million cooperative agreement aimed at strengthening health information systems across more than 25 countries. It focuses on improving data collection, analysis, and use to enhance decision-making and health outcomes. The project includes rigorous evaluation methods to assess the program's impact and cost-effectiveness.