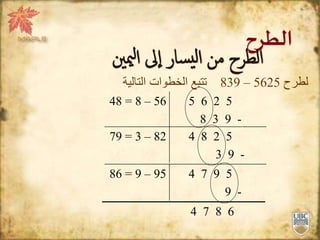
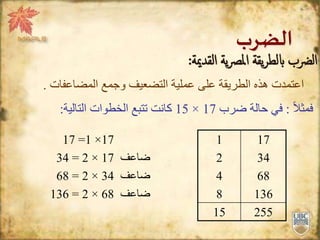
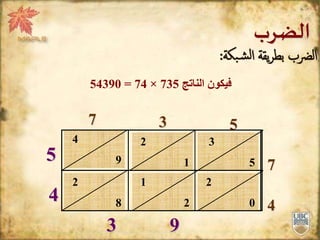
تناقش الوثيقة طرق عمليات الجمع والطرح والضرب والقسمة المستخدمة عبر التاريخ، مع التركيز على الطرق القديمة التي استخدمها العرب. توضح الوثيقة كيفية الجمع باستخدام الأرقام والتحقق من صحة الناتج، بالإضافة إلى تفاصيل حول طرق الضرب المختلفة مثل الطريقة المصرية القديمة والطريقة الشبكية. كما تشرح طرق القسمة القديمة وتعتمد على التضعيف والتصنيف للوصول إلى النتائج.

1. ‫الصحيحة‬ ‫لألعداد‬ ‫الحسابية‬ ‫العمليات‬

2. ‫الجمع‬:
‫مجموع‬ ‫إليجاد‬
2،5،32،193،18،10،100
‫التالية‬ ‫الخطوات‬ ‫تتبع‬ ‫كانت‬:
‫ندية‬‫له‬‫ا‬ ‫يقة‬‫ر‬‫ابلط‬ ‫امجلع‬:
‫اآلحاد‬ ‫مجموع‬=2+5+2+3+8+0+0=20
‫العشرات‬ ‫مجموع‬=3+9+1+1+0=14
‫المئات‬ ‫مجموع‬=1+1=2
‫المجاميع‬ ‫مجموع‬=360

3. ‫الجمع‬:
‫كان‬‫العرب‬‫يكتبون‬‫المجموع‬‫أعلى‬‫األعداد‬‫المجموعة‬‫كما‬
‫كانوا‬‫يستخدمون‬‫مجموع‬‫األرقام‬‫للتحقق‬‫من‬‫صحة‬
‫الناتج‬.
‫فلجمع‬‫العددين‬5687+2343‫كانت‬‫تتبع‬‫الخطوات‬‫التالي‬‫ة‬:
‫ية‬‫ب‬‫ر‬‫الع‬ ‫يقة‬‫ر‬‫ابلط‬ ‫امجلع‬:
2 8030
8
3
5687
2343

4. ‫الجمع‬:
‫ية‬‫ب‬‫ر‬‫الع‬ ‫يقة‬‫ر‬‫ابلط‬ ‫امجلع‬:
2 8030
8
3
5687
2343
‫العمود‬‫األخير‬‫يوضح‬‫طريقة‬‫التحقق‬‫بجمع‬
‫أرقام‬‫كل‬‫عدد‬‫كالتالي‬:
‫بالنسبة‬‫للعدد‬5687‫يكون‬:
7+8+6+5=26،6+2=8
‫بالنسبة‬‫للعدد‬2343‫يكون‬:
3+4+3+2=12،2+1=3
8+3=11،1+1=2
‫وبجمع‬‫أرقام‬‫المجموع‬8030:30+3+0+8=11،1+1=2
‫ولكن‬‫هذه‬‫الطريقة‬‫ليست‬‫صحيحة‬‫دائما‬

5. ‫الجمع‬:
‫ية‬‫ب‬‫ر‬‫الع‬ ‫يقة‬‫ر‬‫ابلط‬ ‫امجلع‬:
‫أخرى‬ ‫وبطريقة‬:
‫المجاميع‬ ‫تجمع‬ ‫ثم‬ ‫منفصال‬ ‫عمود‬ ‫كل‬ ‫مجموع‬ ‫فيها‬ ‫يكتب‬ ‫كان‬.
‫وكانت‬‫األعداد‬‫األكبر‬‫تكتب‬‫من‬‫أعلى‬.
‫كما‬‫كانت‬‫توضع‬‫نقاط‬‫لبيان‬‫عملية‬‫الحمل‬‫من‬‫خانة‬‫أخرى‬.
‫والمثال‬‫التالي‬‫يوضح‬‫هذه‬‫الطريقة‬.

6. ‫الجمع‬:
‫ية‬‫ب‬‫ر‬‫الع‬ ‫يقة‬‫ر‬‫ابلط‬ ‫امجلع‬:
8379
968
34
21
16
12
8
9381
‫لنجمع‬8379+968+34

7. ‫الطرح‬
2212
4311
8
2212
4311
8
‫املطروح‬ ‫العدد‬ ‫اىل‬ ‫ضافة‬‫إ‬‫ال‬‫ا‬‫و‬ ‫تالف‬‫س‬‫ابال‬ ‫الطرح‬‫منه‬:
*2–4‫ال‬‫تصلح‬.‫نستلف‬1‫من‬‫خانة‬‫العشرات‬(2)
‫ونرده‬‫إلى‬‫خانة‬‫العشرات‬‫في‬‫العدد‬‫السفلي‬‫فيص‬‫بح‬4.
*2–4‫ال‬‫تصلح‬.‫نستلف‬1‫من‬‫خانة‬‫المئات‬(1)
‫ونردها‬‫خانة‬‫المئات‬‫في‬‫العدد‬‫السفلي‬‫فيصبح‬2.
42
2212
4311
‫لطرح‬2122–1134:
‫ويكون‬12–4=8
‫ويكون‬12–4=8

8. ‫الطرح‬
2212
4311
9
‫املطروح‬ ‫العدد‬ ‫اىل‬ ‫ضافة‬‫إ‬‫ال‬‫ا‬‫و‬ ‫تالف‬‫س‬‫ابال‬ ‫الطرح‬‫منه‬:
*1–2‫ال‬‫تصلح‬.‫نستلف‬1‫من‬‫خانة‬‫اآلالف‬(2)
‫ونرده‬‫إلى‬‫خانة‬‫اآلالف‬‫في‬‫العدد‬‫السفلي‬‫فيصبح‬2.
*2–2=0
42
2212
4311
88
‫لطرح‬2122–1134:
‫ويكون‬11–2=9
‫ويكون‬‫ناتج‬‫الطرح‬=988
2
‫وهذه‬‫الطريقة‬‫استخدمها‬‫العرب‬‫مثل‬‫القلصاوي‬

9. ‫الطرح‬
82–3=79 5284
-93
56–8=48 5265
-938
6874
‫ميني‬‫ل‬‫ا‬ ‫ىل‬‫إ‬‫ا‬ ‫سار‬‫لي‬‫ا‬ ‫من‬ ‫الطرح‬
‫لطرح‬5625–839‫تتبع‬‫الخطوات‬‫التالية‬
95–9=86 5974
-9

10. ‫الضرب‬
‫نشأت‬‫عملية‬‫الضرب‬‫كعملية‬‫جمع‬‫ي‬‫ار‬‫ر‬‫تك‬‫ومضاعفات‬‫لألعداد‬
‫الصحيحة‬:
*‫الضرب‬‫بالطريقة‬‫المصرية‬‫القديمة‬.
*‫الضرب‬‫بطريقة‬‫المعداد‬.
*‫الضرب‬‫التصالبي‬.
*‫الضرب‬‫بطريقة‬‫الشبكة‬
*‫الضرب‬‫بطريقة‬‫التجزيء‬.

11. ‫الضرب‬
‫الرضب‬‫يقة‬‫ر‬‫ابلط‬‫ية‬‫رص‬‫امل‬‫القدمية‬:
‫اعتمدت‬‫هذه‬‫الط‬‫ريقة‬‫على‬‫عملية‬‫التضعيف‬‫وجمع‬‫المضاعفات‬.
‫فمثال‬:‫في‬‫حالة‬‫ضرب‬17×15‫كانت‬‫تتبع‬‫الخطوات‬‫التالية‬:
17×1=17 1 17
17×2=34 ‫ضاعف‬ 2 34
34×2=68 ‫ضاعف‬ 4 68
68×2=136 ‫ضاعف‬ 8 136
15 255

12. ‫الضرب‬
‫الرضب‬‫يقة‬‫ر‬‫ابلط‬‫ية‬‫رص‬‫امل‬‫القدمية‬:
‫وهذا‬‫يعني‬‫أن‬‫حاصل‬‫ضرب‬17×15‫يعني‬‫تكرار‬‫العدد‬(17)15‫مرة‬.
ً‫وأحيانا‬‫كانوا‬‫يكررون‬‫العدد‬(17)16‫مرة‬‫ثم‬‫يطرحون‬‫من‬‫الناتج‬‫العدد‬17‫كما‬‫يلي‬:
1 17
2 34
4 68
8 136
‫العدد‬17‫مكرر‬16‫مرة‬ 16 272
‫العدد‬17‫واحدة‬ ‫مرة‬ ‫طرح‬ 1 -17
‫العدد‬17‫مكرر‬15‫مرة‬ 15 255

13. ‫الضرب‬
‫الرضب‬‫يقة‬‫ر‬‫بط‬‫املعداد‬:‫كانت‬‫عملية‬‫الضرب‬‫تتم‬‫على‬‫جدول‬‫يشبه‬‫لوحة‬‫الشطرنج‬.
ً‫فمثل‬‫لضرب‬4600×23‫كانت‬‫تتبع‬‫الخطوات‬‫التالية‬:
CM
‫اآلالف‬ ‫مئات‬
XM
‫اآلالف‬ ‫عشرات‬
M
‫آالف‬
C
‫مئات‬
X
‫عشرات‬
I
‫آحاد‬
4600 4 6
3×6
2×6
3×4
2×4
1
1
8
1
2
2
8
‫الضرب‬ ‫حاصل‬ 10 5 8
×23 2 3

14. ‫الضرب‬
‫الرضب‬‫يقة‬‫ر‬‫بط‬‫املعداد‬:
ً‫وبذلكًيكونًالناتج‬4600×23=105800
XM
‫اآلالف‬ ‫مئات‬
XM
‫اآلالف‬ ‫عشرات‬
M
‫آالف‬
C
‫مئات‬
X
‫عشرات‬
I
‫آحاد‬
4600 4 6
3×6
2×6
3×4
2×4
1
1
8
1
2
2
8
‫الضرب‬ ‫حاصل‬ 10 5 8
×23 2 3

15. ‫الضرب‬
3
2
2
5
‫الرضب‬‫تصاليب‬‫ل‬‫ا‬:
‫استخدم‬‫باسيولي‬1494‫هذه‬‫الطريقة‬‫في‬‫الضرب‬،‫وهي‬‫طريقة‬‫صعبة‬‫تحتاج‬
‫إلى‬‫قدرات‬‫عددية‬‫كبيرة‬‫خاصة‬‫إذا‬‫كانت‬‫األعداد‬‫مكونة‬‫من‬‫أرقام‬‫عديدة‬.
800
5×2=10
5×30=150
20×2=40
20×30=600
ً‫فمثل‬:‫إليجاد‬32×25‫نتبع‬‫الخطوات‬‫التالية‬:

16. ‫الضرب‬
94 12 53
82 21 02
‫الرضب‬‫يقة‬‫ر‬‫بط‬‫بكة‬‫ش‬‫ل‬‫ا‬:
‫استخدم‬‫الهنود‬‫والعرب‬‫والصينيون‬‫واألوربيون‬‫هذه‬‫الطريقة‬.
ً‫فمثل‬:‫إليجاد‬735×74‫نتبع‬‫الخطوات‬‫التالية‬:
7
3
5
2
1
4
9
2
0
1
2
2
8 4
7 3 5
93
4
5

17. ‫الضرب‬
94 12 53
82 21 02
‫الرضب‬‫يقة‬‫ر‬‫بط‬‫بكة‬‫ش‬‫ل‬‫ا‬:
ً‫فيكونًالناتج‬735×74=54390
7
3
5
2
1
4
9
2
0
1
2
2
8 4
7 3 5
93
4
5

18. ‫الضرب‬
‫الرضب‬‫يقة‬‫ر‬‫بط‬‫تجزيء‬‫ل‬‫ا‬:
‫استخدم‬‫األغريق‬‫والعرب‬‫هذه‬‫الطريقة‬.
ً‫فمثل‬:‫إليجاد‬‫حاصل‬‫ضرب‬265×143‫نتبع‬‫الخطوات‬‫التالية‬:
20024008000
500600020000
562
341
ً‫أيًأن‬265×143=37895
15018600
715858028600=37895
100 40
200 60

19. ‫القسمة‬
‫المصريين‬ ‫القدماء‬ ‫بطريقة‬ ‫القسمة‬.
‫جربرت‬ ‫بطريقة‬ ‫القسمة‬.
‫امل‬‫و‬‫الع‬ ‫على‬ ‫القسمة‬ ‫طريقة‬.
‫العربية‬ ‫بالطريقة‬ ‫القسمة‬.
‫جالي‬ ‫بطريقة‬ ‫القسمة‬(‫اعية‬‫ر‬‫الش‬ ‫السفينة‬.)

20. ‫القسمة‬
‫سمة‬‫لق‬‫ا‬‫عىل‬‫يقة‬‫ر‬‫ط‬‫القدماء‬‫يني‬‫رص‬‫امل‬:
‫تعد‬‫هذه‬‫الطريقة‬‫من‬‫أقدم‬‫طرق‬‫القسمة‬‫وكانت‬‫تعتمد‬‫على‬‫التضعيف‬
‫والتصنيف‬.
ً‫فمثل‬:‫إليجاد‬19÷8‫نتبع‬‫الخطوات‬‫التالية‬:
‫نبحث‬‫عن‬‫أعداد‬‫تضرب‬‫في‬8‫بحيث‬‫يكون‬‫الناتج‬ً‫قريبا‬‫من‬19‫ونسير‬‫كاآلتي‬

21. ‫القسمة‬
‫سمة‬‫لق‬‫ا‬‫عىل‬‫يقة‬‫ر‬‫ط‬‫القدماء‬‫يني‬‫رص‬‫امل‬:
4
16
ًً‫أيًأن‬19÷8=3/82
2
8
1
3/82
8×2=16
1
2
1/2
1/4
1/8
19
8×1/4=2
8×1/8=1
2+1/4+1/8=3/82

22. ‫القسمة‬
‫سمة‬‫لق‬‫ا‬‫عىل‬‫يقة‬‫ر‬‫ط‬‫برت‬‫ر‬‫ج‬:
‫تنسب‬‫هذه‬‫الطريقة‬‫الى‬‫جربرت‬980‫م‬‫وهي‬‫شبيهة‬‫بالقسمة‬‫المطولة‬.
ً‫فمثل‬:‫إليجاد‬900÷8‫نتبع‬‫الخطوات‬‫التالية‬:
‫نجري‬‫العملية‬‫باعتبار‬8=10-2‫ونسير‬‫كاآلتي‬

23. ‫القسمة‬
‫سمة‬‫لق‬‫ا‬‫عىل‬‫يقة‬‫ر‬‫ط‬‫برت‬‫ر‬‫ج‬:
900 10-2
900-180
90
180
180-36
+18
36
+3
30-6
6+6=12
+1
10-2
2+2=4
=½112 +(4/8)

24. ‫القسمة‬
‫يقة‬‫ر‬‫ط‬‫سمة‬‫لق‬‫ا‬‫عىل‬‫امل‬‫و‬‫الع‬:
‫استخدمت‬‫هذه‬‫الطريقة‬‫في‬‫العصور‬‫الوسطى‬.
‫تعتمد‬‫هذه‬‫الطريقة‬‫على‬‫قسمة‬‫العدد‬‫المقسوم‬‫على‬‫عوامل‬‫المقسوم‬‫عليه‬.
‫والمثال‬‫التالي‬‫يوضح‬‫كيفية‬‫السير‬‫في‬‫هذه‬‫الطريقة‬:
‫لقسمة‬216÷24‫نتبع‬‫الخطوات‬‫التالية‬:
24=8×3
216÷8=27
27÷3=9
ًًً‫وبذلكًيكون‬216÷24=9