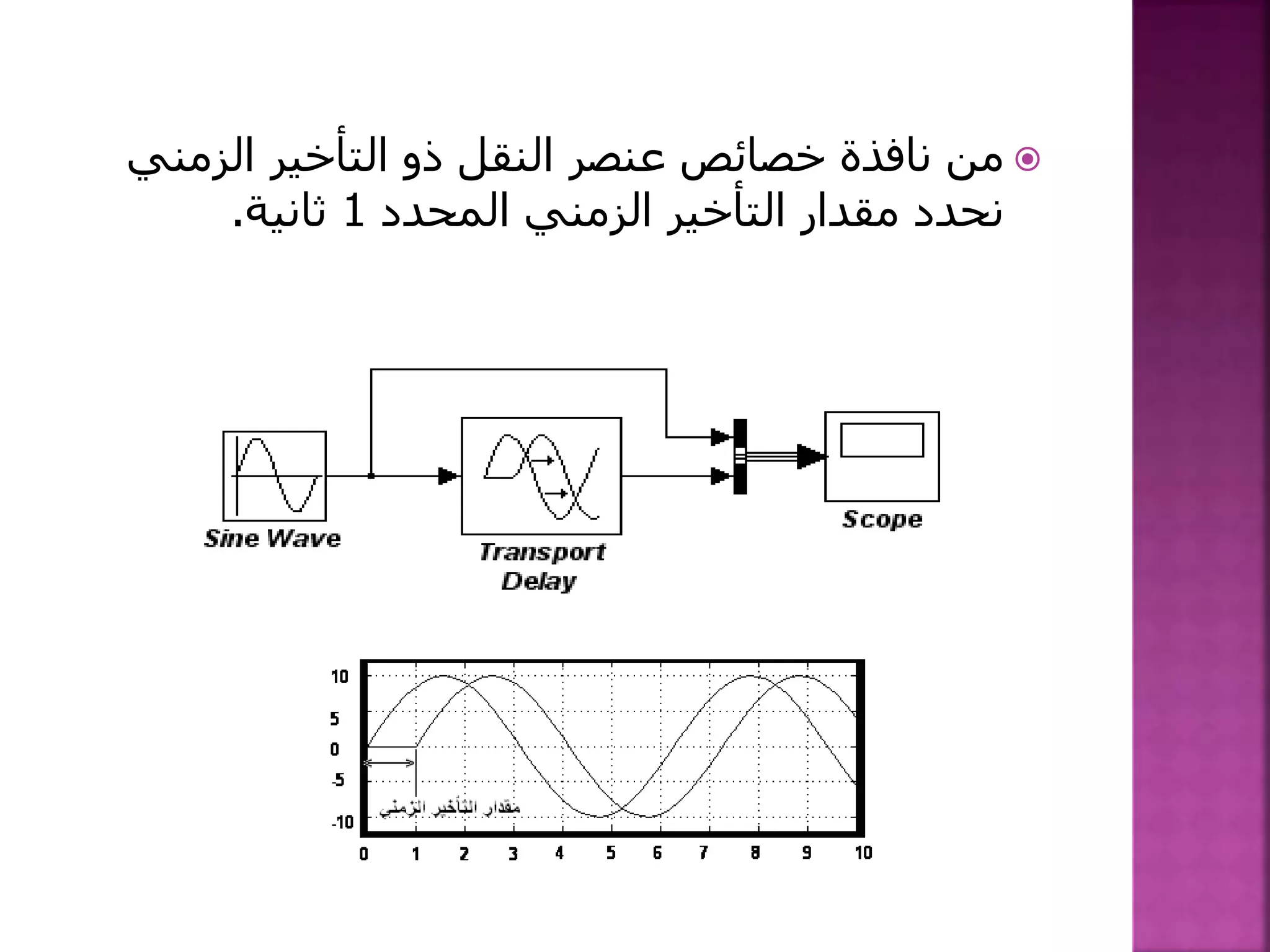
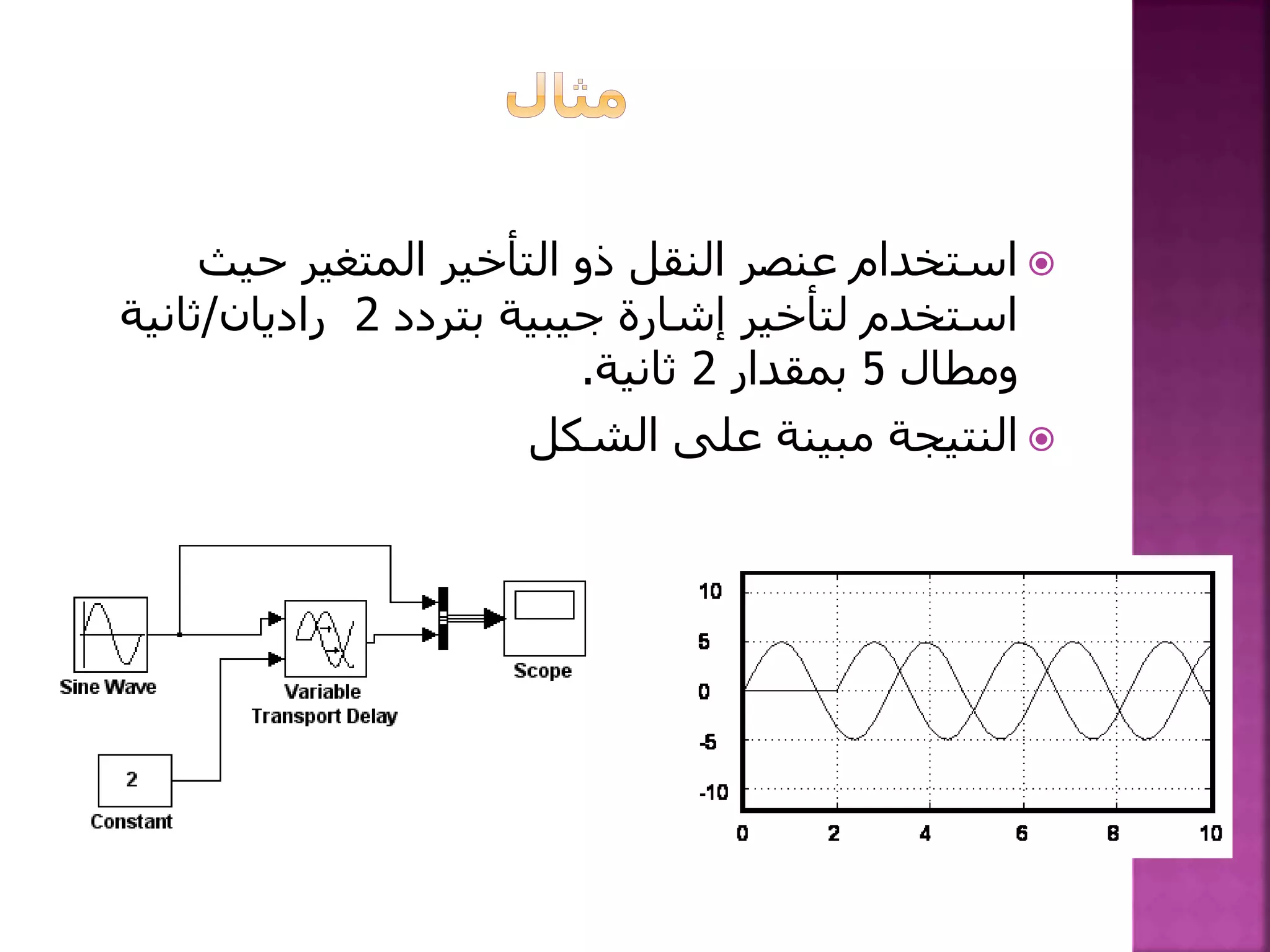
يتناول الوثيقة مفهوم التكامل في المعادلات التفاضلية، موضحًا كيفية بناء نموذج تكاملي بناءً على شروط ابتدائية وخصائص العناصر المستخدمة. يتضمن الوثيقة خطوات لحل المعادلات من خلال عملية تجميع العناصر وإدخال إشارات معينة لضبط النتائج. كما يوضح استخدام simulink لتصميم الأنظمة الديناميكية مع التركيز على العمليات المطبقة على العناصر التفاعلية.

1. ‫اعداد‬:‫م‬.‫حسن‬‫ادريس‬

2. ‫تحتوي‬‫المكتبة‬ ‫هذه‬‫المناصر‬ ‫على‬‫الخطية‬
‫المستمرة‬‫المرتبطة‬‫بالزمن‬‫و‬‫ا‬‫المستمرة‬ ‫لعناصر‬
‫ذات‬‫الزمني‬ ‫التأخير‬.

4. ‫التكامل‬ ‫عنصر‬ ‫يقوم‬‫بمكاملة‬‫ز‬ ‫المستمر‬ ‫التابع‬ً‫منيا‬
‫دخله‬ ‫على‬ ‫والمطبق‬.
‫تابعة‬ ‫واحدة‬ ‫حالة‬ ‫عن‬ ‫عبارة‬ ‫التكامل‬ ‫صندوق‬ ‫دخل‬
‫للزمن‬.
‫يقوم‬‫بمكاملة‬‫الحالية‬ ‫الزمن‬ ‫خطوة‬ ‫وفق‬ ‫الدخل‬
‫الحالي‬ ‫االبتدائية‬ ‫الشروط‬ ‫وفق‬ ‫وكذلك‬ ‫للتكامل‬‫ة‬.
‫ص‬ ‫هي‬ ‫للتكامل‬ ‫االفتراضية‬ ‫االبتدائية‬ ‫القيمة‬‫فر‬.
‫االبتدائية‬ ‫للحالة‬ ‫خاصة‬ ‫قيم‬ ‫وضع‬ ‫يمكن‬

5. ‫التكامل‬ ‫عنصر‬ ‫خصائص‬

6. ‫القي‬ ‫بتحديد‬ ‫تسمح‬ ‫االبتدائية‬ ‫الشروط‬ ‫تحديد‬ ‫إلى‬ ‫باإلضافة‬‫الدنيا‬ ‫م‬
‫التكامل‬ ‫لحدود‬ ‫والعليا‬.‫ع‬ ‫نحصل‬ ‫أن‬ ‫يمكن‬ ‫الخيارات‬ ‫لهذه‬ ً‫وتبعا‬‫لى‬
‫الشكل‬ ‫في‬ ‫والمبينة‬ ‫التكامل‬ ‫لعنصر‬ ‫المختلفة‬ ‫األشكال‬
‫صندوق‬‫التكامل‬‫في‬‫الحالة‬‫اضية‬‫ر‬‫االفت‬.Integrator-1
-Initial condition source: external
-‫بقية‬‫المعطيات‬‫اضية‬‫ر‬‫افت‬.Integrator-2
-Limit output: check mark.
-‫بقية‬‫المعطيات‬‫اضية‬‫ر‬‫افت‬.Integrator-3
-External reset: rising.
-‫بقية‬‫المعطيات‬‫اضية‬‫ر‬‫افت‬Integrator-4
-External reset: falling.
-‫بقية‬‫المعطيات‬‫اضية‬‫ر‬‫افت‬Integrator-5
-External reset: either.
-‫بقية‬‫المعطيات‬‫اضية‬‫ر‬‫افت‬Integrator-6
-External reset: level.
-‫بقية‬‫المعطيات‬‫اضية‬‫ر‬‫افت‬Integrator-7
-Show state port: check mark.
-‫بقية‬‫المعطيات‬‫اضية‬‫ر‬‫افت‬Integrator-8
- External reset: rising
- Initial condition source: external
- Limit output : check mark
- Show saturation port: check mark
- Show state port : check mark
Integrator-9

7. ‫الدرجة‬ ‫من‬ ‫التفاضلية‬ ‫المعادالت‬ ‫حل‬ ‫يمكن‬n‫المكتوبة‬
‫الشكل‬ ‫على‬:
‫التالية‬ ‫الخطوات‬ ‫وفق‬ ‫وذلك‬:
1–‫األ‬ ‫الطرف‬ ‫في‬ ‫يكون‬ ‫ال‬ ‫بحيث‬ ‫المعادلة‬ ‫كتابة‬ ‫نعيد‬‫يسر‬
‫على‬ ‫تصبح‬ ‫وبحيث‬ ‫األعلى‬ ‫الدرجة‬ ‫ذو‬ ‫التفاضل‬ ‫إال‬
‫الشكل‬:
2–‫للمعادلة‬ ‫الثاني‬ ‫الطرف‬ ‫حدود‬ ‫جميع‬ ‫ندخل‬(**)‫على‬
‫تجميع‬ ‫عنصر‬.
(*)...... 011
1
1 ba
dt
dx
a
dt
xd
a
dt
xd
a n
n
nn
n
n  


(**)...... 01
1
1
1
nnn
n
n
n
n
n
n
a
b
a
a
dt
dx
a
a
dt
xd
a
a
dt
xd
 



8. 3–‫دخل‬ ‫على‬ ‫التجميع‬ ‫عنصر‬ ‫خرج‬ ‫إشارة‬ ‫ندخل‬
‫عناص‬ ‫عدد‬ ،‫التسلسل‬ ‫على‬ ‫متصلة‬ ‫تكامل‬ ‫عناصر‬‫ر‬
‫التفاضلي‬ ‫المعادلة‬ ‫لدرجة‬ ‫مساويا‬ ‫يكون‬ ‫التكامل‬‫ة‬.
4–‫التجميع‬ ‫عنصر‬ ‫دخل‬ ‫إشارات‬ ‫على‬ ‫الحصول‬ ‫يتم‬
‫ربح‬ ‫مضخمات‬ ‫عبر‬ ‫التكامل‬ ‫عناصر‬ ‫خرج‬ ‫من‬gain
‫حد‬ ‫بكل‬ ‫الخاصة‬ ‫العوامل‬ ‫حسب‬.

9. ‫التفاضلية‬ ‫المعادلة‬ ‫لحل‬ ‫نموذج‬ ‫وضع‬ ‫المطلوب‬
‫التالية‬:
‫صفرية‬ ‫االبتدائية‬ ‫الشروط‬.
103025115 2
2
3
3
4
4
 y
dt
dy
dt
yd
dt
yd
dt
yd

10. 1–‫الط‬ ‫في‬ ‫يكون‬ ‫ال‬ ‫بحيث‬ ‫المعادلة‬ ‫كتابة‬ ‫نعيد‬‫رف‬
‫تص‬ ‫وبحيث‬ ‫األعلى‬ ‫الدرجة‬ ‫ذو‬ ‫التفاضل‬ ‫إال‬ ‫األيسر‬‫بح‬
‫الشكل‬ ‫على‬:
2–‫تجميع‬ ‫عنصر‬ ‫على‬ ‫األيمن‬ ‫الطرف‬ ‫عناصر‬ ‫ندخل‬
‫الشكل‬ ‫في‬ ‫مبين‬ ‫هو‬ ‫كما‬
103025115 2
2
3
3
4
4
 y
dt
dy
dt
yd
dt
yd
dt
yd

11. 3–‫الخرج‬ ‫في‬ ‫نضيف‬4‫من‬‫المكامالت‬‫يساوي‬ ‫وهذا‬
‫التفاضلية‬ ‫المعادلة‬ ‫درجة‬

12. –‫التجميع‬ ‫عنصر‬ ‫دخل‬ ‫إشارات‬ ‫على‬ ‫الحصول‬ ‫يتم‬
‫ربح‬ ‫مضخمات‬ ‫عبر‬ ‫التكامل‬ ‫عناصر‬ ‫خرج‬ ‫من‬gain
‫حد‬ ‫بكل‬ ‫الخاصة‬ ‫العوامل‬ ‫حسب‬.

13. ‫التفاضلية‬ ‫المعادلة‬ ‫لحل‬ ‫نموذج‬ ‫وضع‬ ‫المطلوب‬
‫التالية‬:
‫االبتدائية‬ ‫الشروط‬. :
)(334 02
2
tuV
dt
dV
dt
Vd
C
CC

0)0(;5.0)0( '
 CC VV

14. ‫باستخدام‬ ‫التفاضلية‬ ‫المعادالت‬ ‫لحل‬Simulink‫الخطوات‬ ‫نتبع‬
‫التالية‬:
1–‫للتفاض‬ ‫األعلى‬ ‫الحد‬ ‫نضع‬ ‫بحيث‬ ‫المعادلة‬ ‫كتابة‬ ‫نعيد‬‫ل‬
،‫الثاني‬ ‫الطرف‬ ‫في‬ ‫الحدود‬ ‫وبقية‬ ‫للمعادلة‬ ‫األول‬ ‫بالطرف‬
‫الشكل‬ ‫على‬ ‫مثالنا‬ ‫في‬ ‫وتصبح‬:
2–‫بث‬ ‫جمع‬ ‫عنصر‬ ‫إليه‬ ‫وننسخ‬ ‫جديد‬ ‫لنموذج‬ ‫نافذة‬ ‫نفتح‬‫الثة‬
‫للمعادلة‬ ‫الثاني‬ ‫الطرف‬ ‫إشارات‬ ‫بعدد‬ ‫وذلك‬ ‫دخل‬ ‫منافذ‬
‫السابقة‬.
3–‫المعادلة‬ ‫درجة‬ ‫تساوي‬ ‫التكامل‬ ‫صناديق‬ ‫من‬ ‫عدد‬ ‫ننسخ‬
‫المميزة‬.
4–‫من‬ ‫كل‬ ‫شكل‬ ‫نحدد‬ ‫التكامل‬ ‫عنصر‬ ‫خصائص‬ ‫نوافذ‬ ‫من‬
‫مرحلة‬ ‫لكل‬ ‫المحددة‬ ‫الشروط‬ ‫وفق‬ ‫التكامل‬ ‫صناديق‬.
5–‫الحالة‬ ‫قيم‬ ‫لوضع‬ ‫الثابتة‬ ‫القيمة‬ ‫صناديق‬ ‫نستخدم‬
‫االبتدائية‬.
6–‫الربح‬ ‫صندوق‬ ‫عنصر‬ ‫ننسخ‬Gain‫بثابت‬ ‫الضرب‬ ‫لتحقيق‬.
7–‫الخرج‬ ‫عناصر‬ ‫نستخدم‬Scope‫الخرج‬ ‫إشارة‬ ‫لرؤية‬.
8–‫الزمني‬ ‫التابع‬ ‫وفق‬ ‫الدخل‬ ‫صندوق‬ ‫ننسخ‬u(t).
)(334 02
2
tuV
dt
dV
dt
Vd
C
CC


16. ‫التقريب‬ ‫القيمة‬ ‫بحساب‬ ‫يقوم‬ ‫التفاضل‬ ‫عنصر‬‫ية‬
‫لدخله‬.
‫صفر‬ ‫هي‬ ‫للخرج‬ ‫االبتدائية‬ ‫القيمة‬ ‫إن‬.
‫الزمن‬ ‫خطوة‬ ‫على‬ ‫تعتمد‬ ‫الدخل‬ ‫نتيجة‬ ‫دقة‬ ‫إن‬
‫التفاضل‬ ‫لحساب‬.

17. ‫الجيب‬ ‫إشارة‬ ‫لتفاضل‬ ‫نموذج‬ ‫وضع‬ ‫المطلوب‬
y = 10cos(2t).

18. ‫الشكل‬ ‫في‬ ‫المبين‬ ‫النموذج‬ ‫نشكل‬.‫إشا‬ ‫ونختار‬‫رة‬
‫الدخل‬‫الجيبية‬‫بمطال‬‫مقداره‬10‫وتردد‬2 rad/sec.

20. ‫عنها‬ ‫يعبر‬ ‫التي‬ ‫النظم‬ ‫لتمثيل‬ ‫أداة‬ ‫عن‬ ‫عبارة‬
‫الت‬ ‫الرياضية‬ ‫الصيغة‬ ‫وفق‬ ‫الحالة‬ ‫فراغ‬ ‫بمعادالت‬‫الية‬:
DuCxy
BuAxx


‫حيث‬:
‫عمودية‬ ‫أشعة‬ ‫عن‬ ‫عبارة‬.
A‫مربعة‬ ‫مصفوفة‬‫بأبعاد‬n * n‫وتشير‬n‫الحاالت‬ ‫عدد‬ ‫إلى‬.
B‫بأبعاد‬ ‫مصفوفة‬n * m‫تشير‬ ‫حيث‬m‫إلى‬‫الدخل‬ ‫إشارات‬ ‫عدد‬.
C‫بأبعاد‬ ‫مصفوفة‬r * n‫حيث‬‫تشير‬r‫الخرج‬ ‫إشارات‬ ‫عدد‬ ‫إلى‬.
D‫مصفوفة‬‫بأبعاد‬r * m

21. ‫فراغ‬ ‫صندوق‬ ‫باستخدام‬ ‫النظام‬ ‫هذا‬ ‫تمثيل‬ ‫المطلوب‬
‫الحالة‬
‫حيث‬:
DuCxy
BuAxx












































4
3
2
1
'
4
'
3
'
2
'
1
;
0201
1000
0100
0010
;
x
x
x
x
xA
x
x
x
x
x
    );(00001;)(;)(
1
0
0
0
4
3
2
1
1 tu
x
x
x
x
yxtytuuandb 



























22. 1–‫صندوق‬ ‫إليه‬ ‫وننسخ‬ ‫جديد‬ ‫موديل‬ ‫نافذة‬ ‫نفتح‬
State-Space Block.
2–‫لفت‬ ‫الصندوق‬ ‫هذا‬ ‫رمز‬ ‫على‬ ً‫مزدوجا‬ ً‫نقرا‬ ‫ننقر‬‫ح‬
‫خصائصه‬ ‫نافذة‬
3–‫ندخل‬‫بارامترات‬‫هو‬ ‫كما‬ ‫الحالة‬ ‫فراغ‬ ‫معادالت‬
‫الخصائص‬ ‫نافذة‬ ‫في‬ ‫مبين‬.
4–‫الدخل‬ ‫إشارة‬ ‫صندوق‬ ‫ننسخ‬sin(t).
5–‫الخرج‬ ‫إشارة‬ ‫صندوق‬ ‫ننسخ‬(Scope)‫و‬(disply)
‫الشكل‬ ‫في‬ ‫المبين‬ ‫النموذج‬ ‫على‬ ‫فنحصل‬.
‫النتائج‬ ‫على‬ ‫نحصل‬ ‫النموذج‬ ‫تشغيل‬ ‫وعند‬

25. ‫ال‬ ‫توابع‬ ‫لتمثيل‬ ‫النقل‬ ‫تابع‬ ‫صندوق‬ ‫يستخدم‬‫نقل‬
‫الخرج‬ ‫مقدار‬ ‫هذه‬ ‫النقل‬ ‫توابع‬ ‫تمثل‬ ‫حيث‬ ‫لألنظمة‬
‫مستوي‬ ‫في‬ ‫الدخل‬ ‫مقدار‬ ‫على‬ ‫مقسوما‬‫البالس‬
‫العالقة‬ ‫وفق‬:
)(
)(
)(
SV
SV
sG
in
out


26. ‫صند‬ ‫باستخدام‬ ‫المبينة‬ ‫الدارة‬ ‫تمثيل‬ ‫المطلوب‬‫وق‬
‫النقل‬ ‫تابع‬.FCCRRR 1;1 21321 

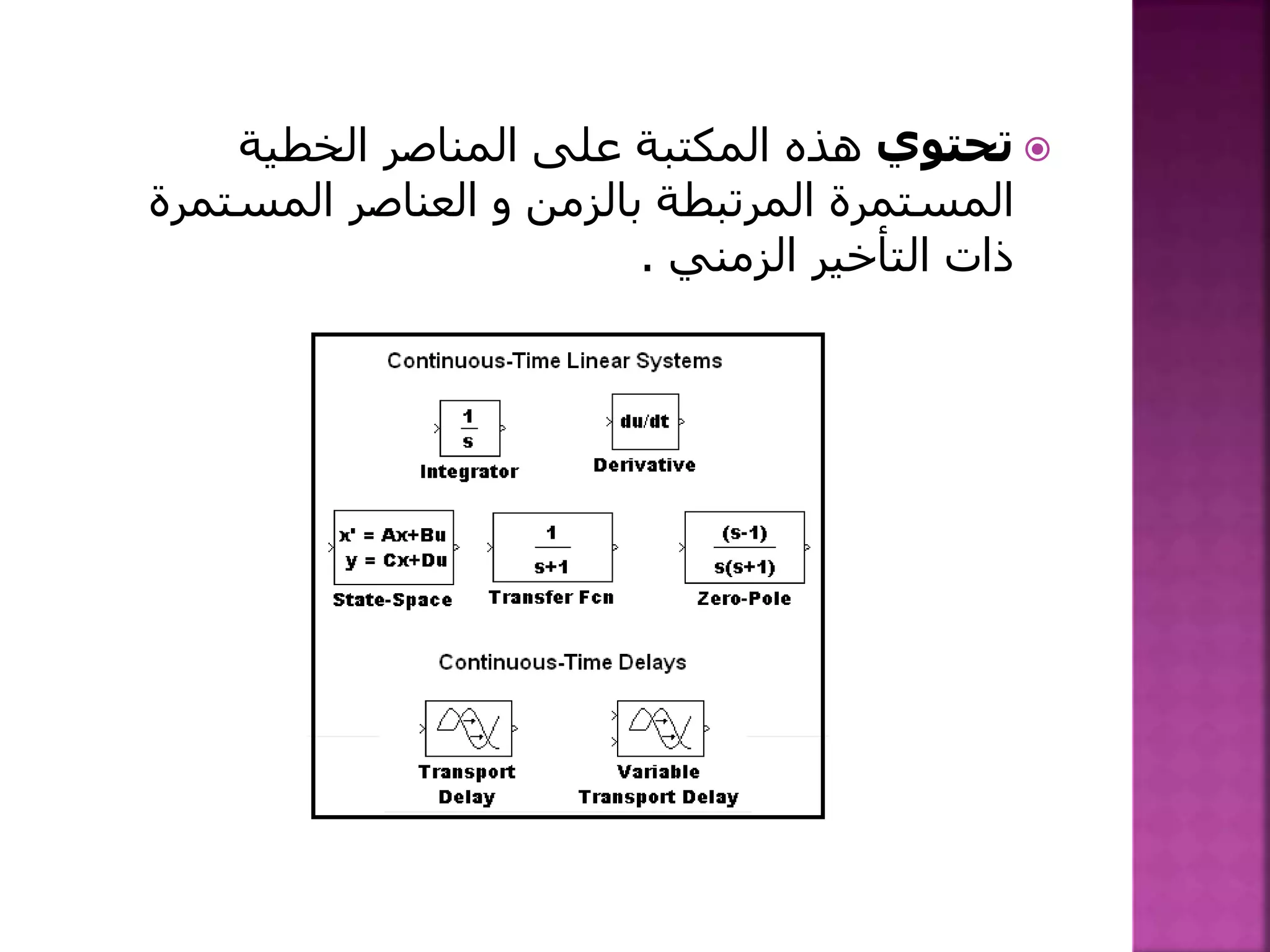
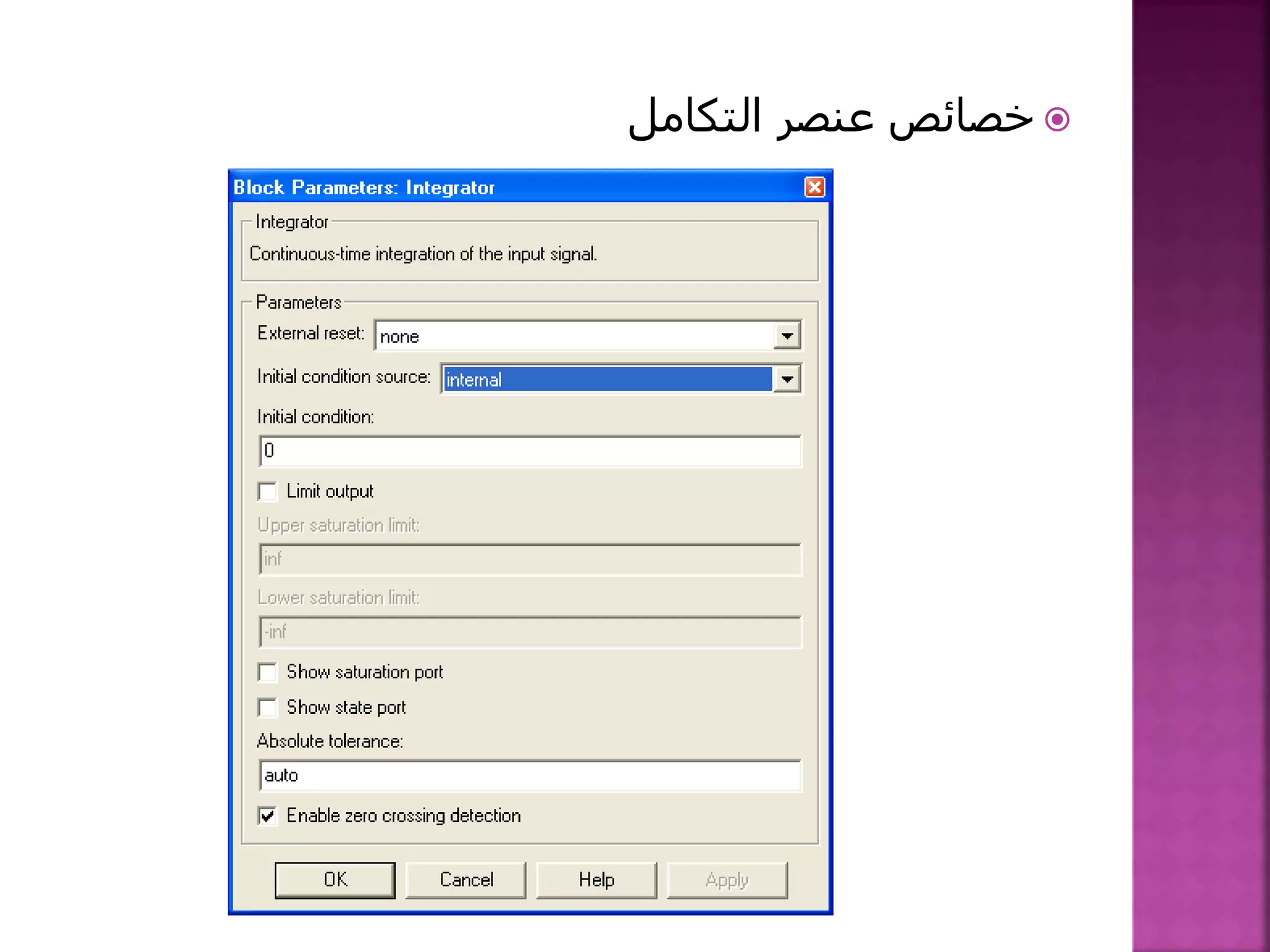
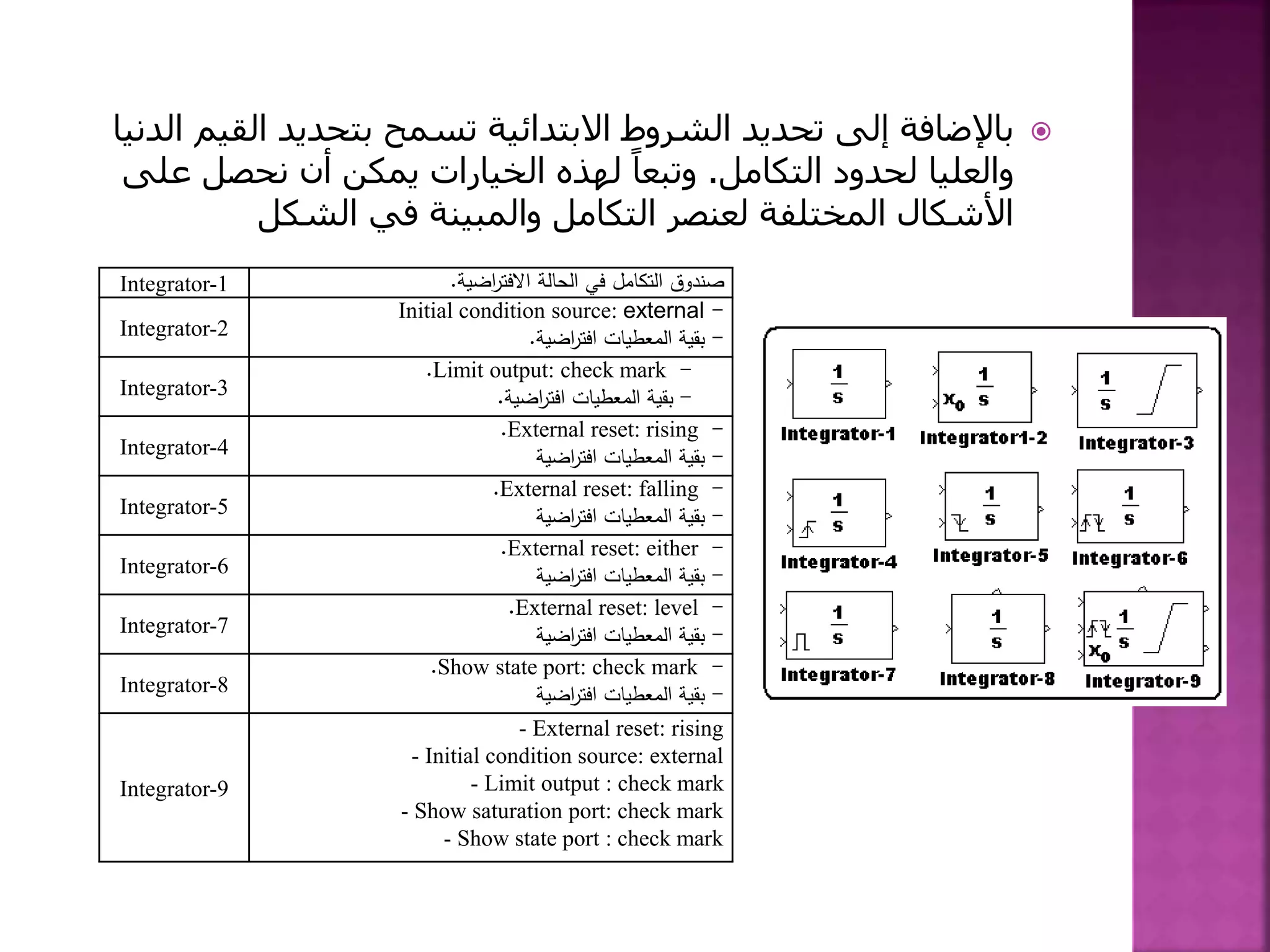
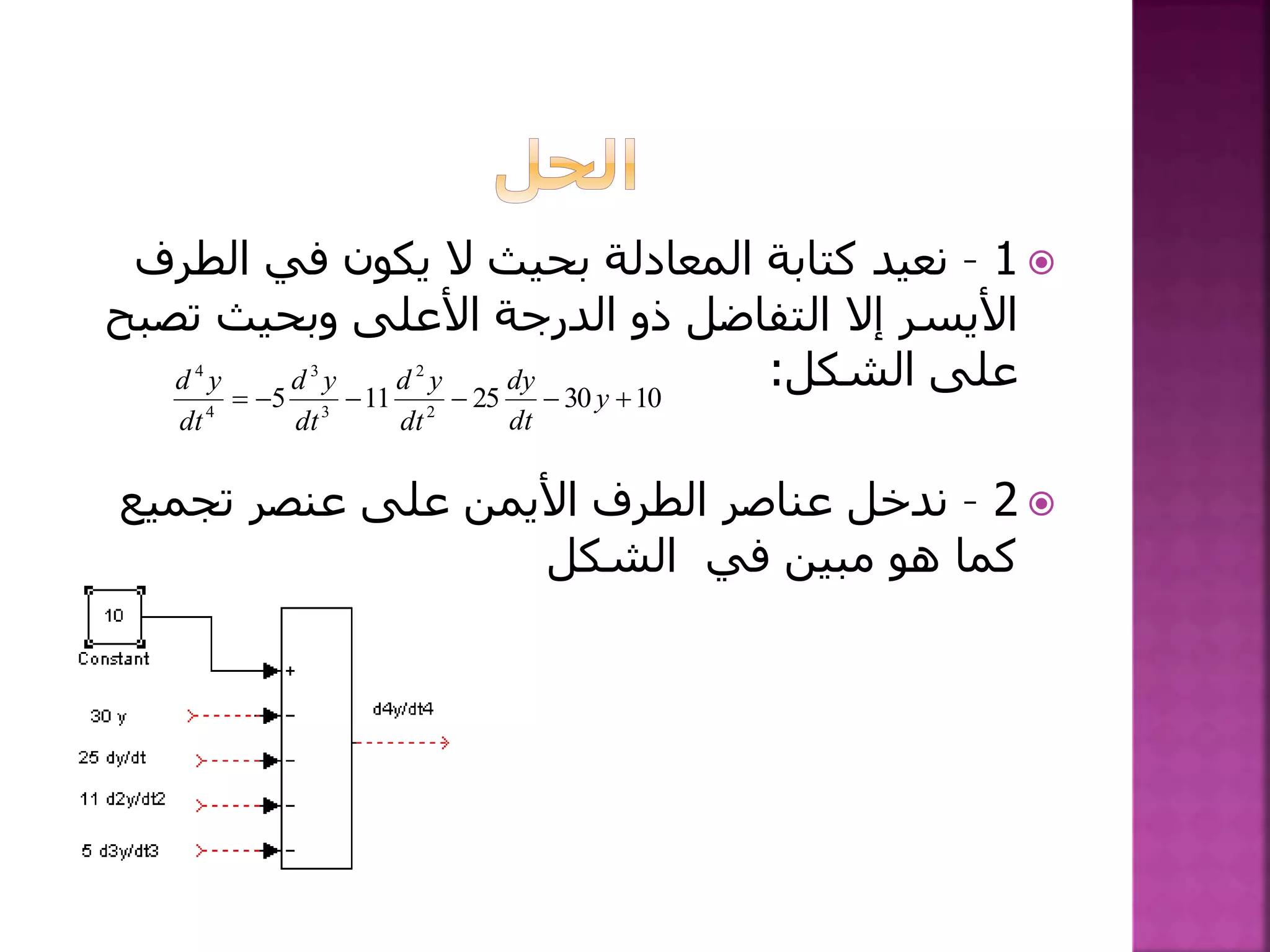
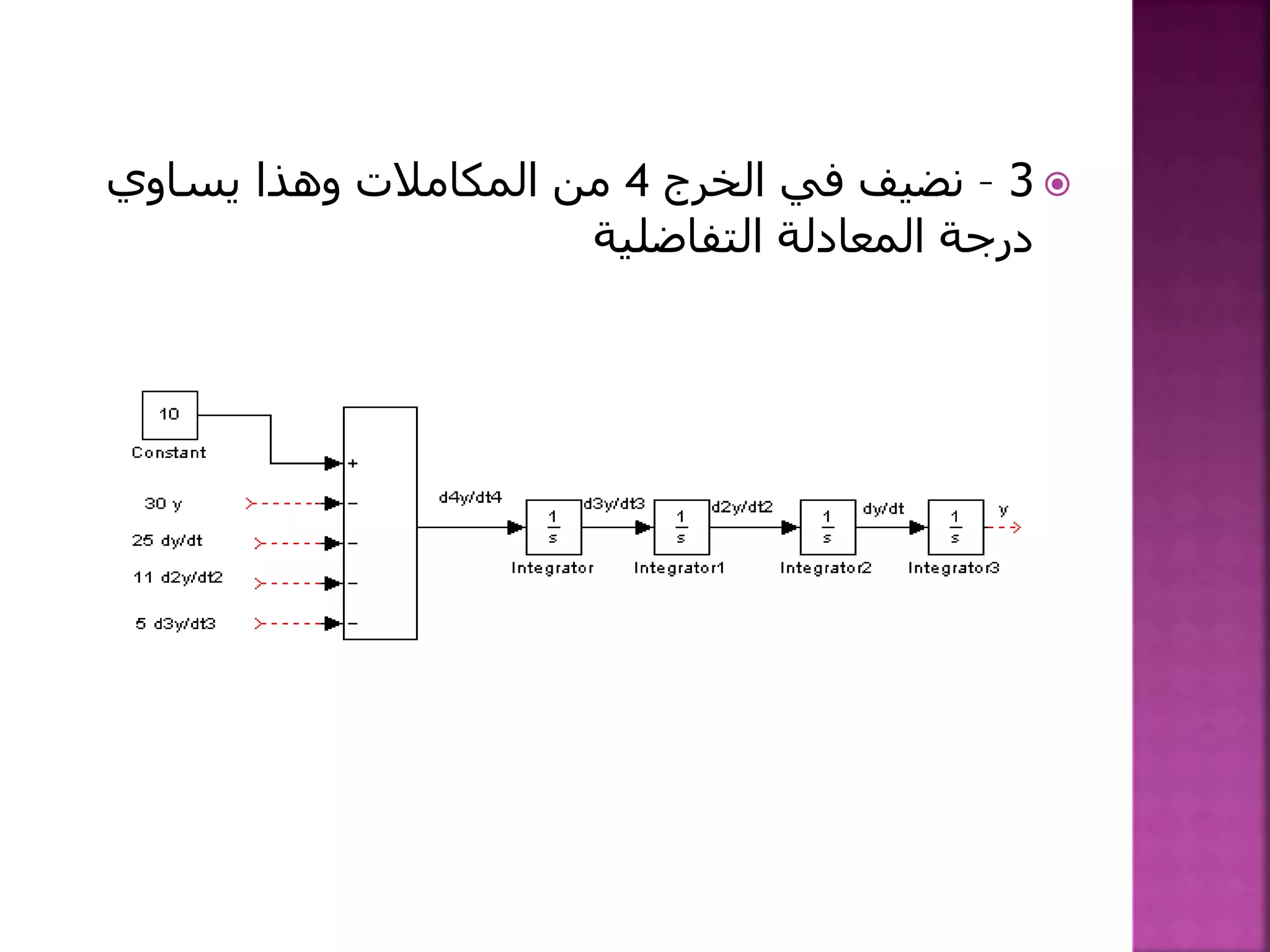
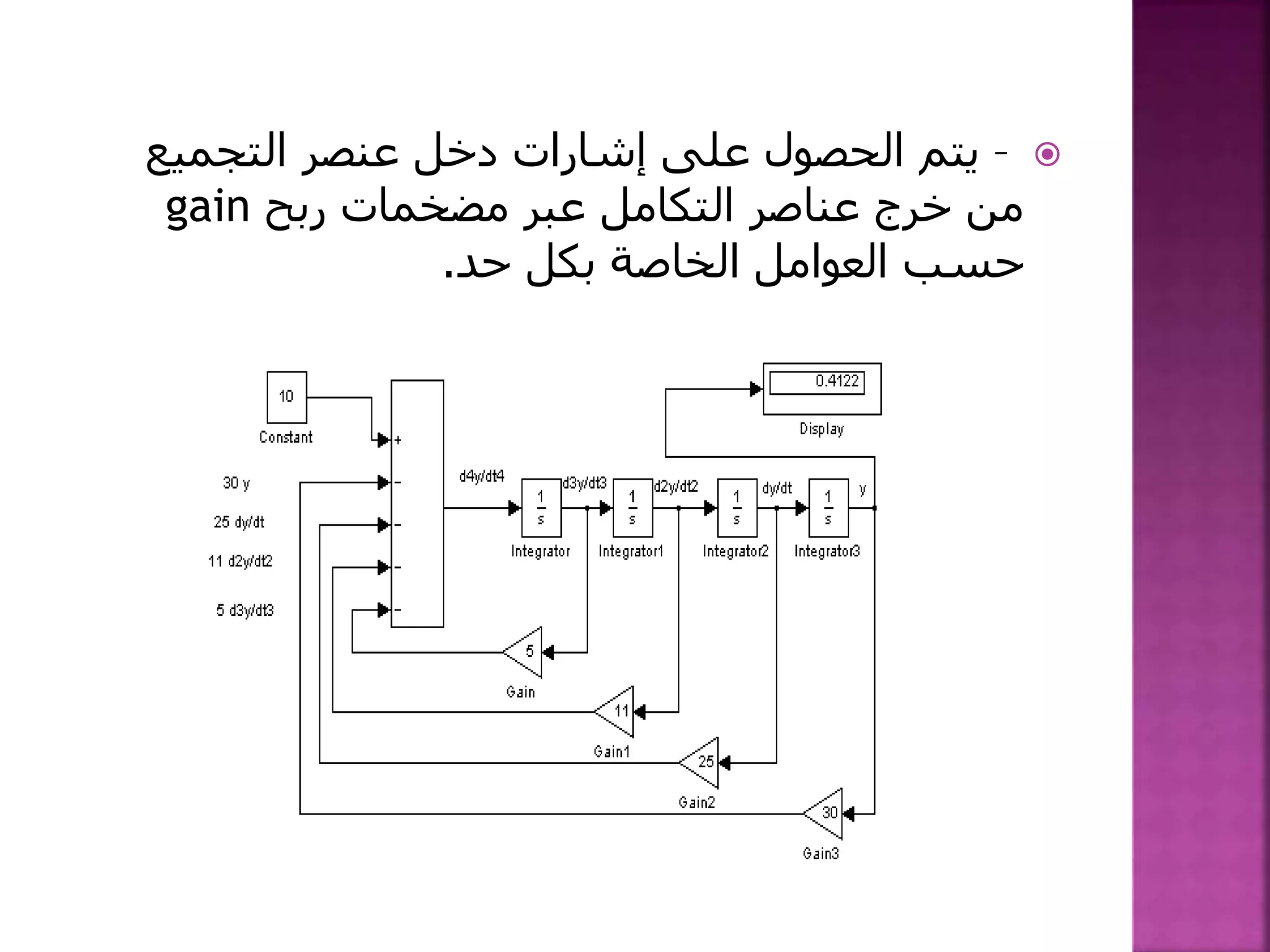
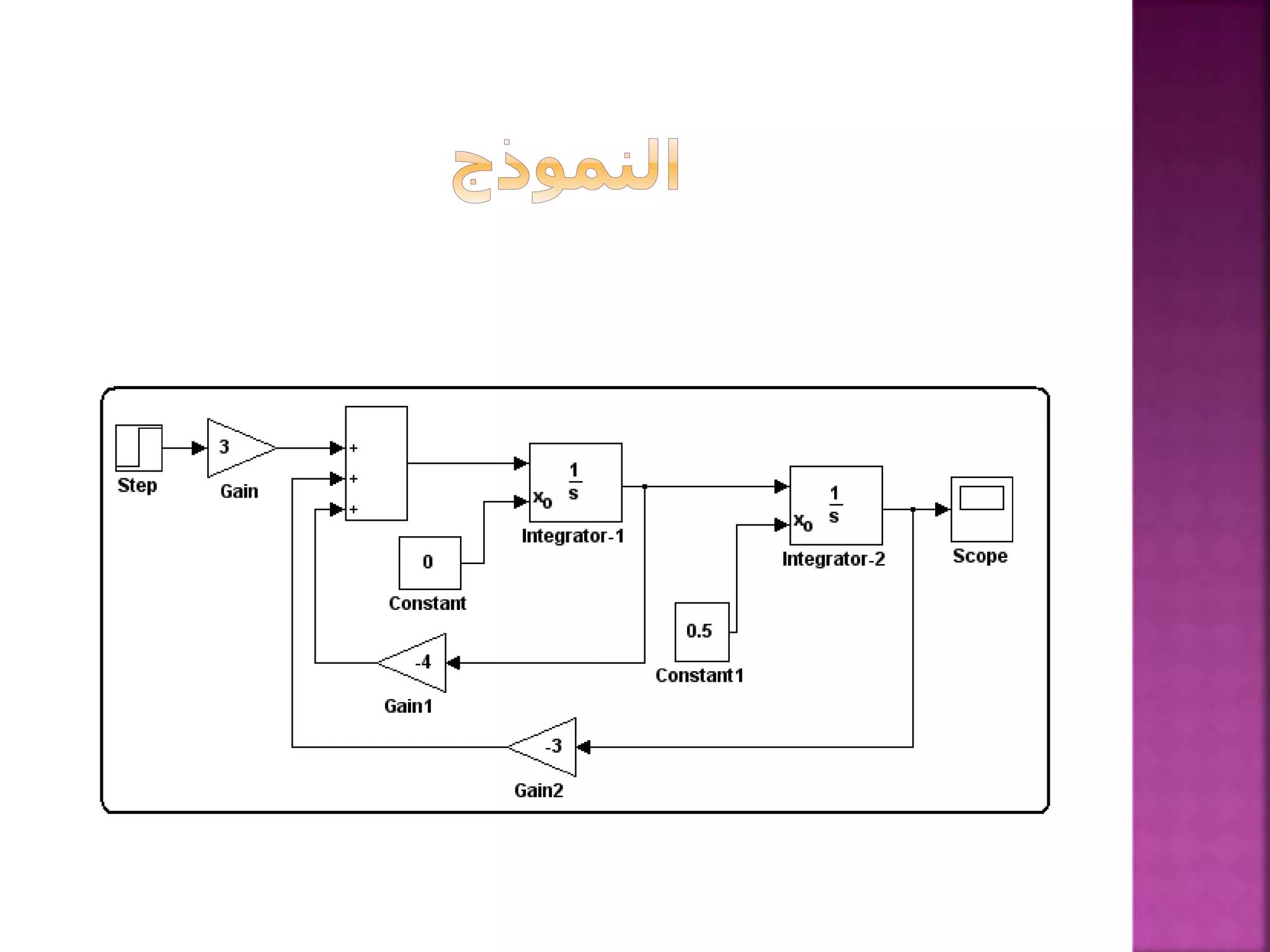
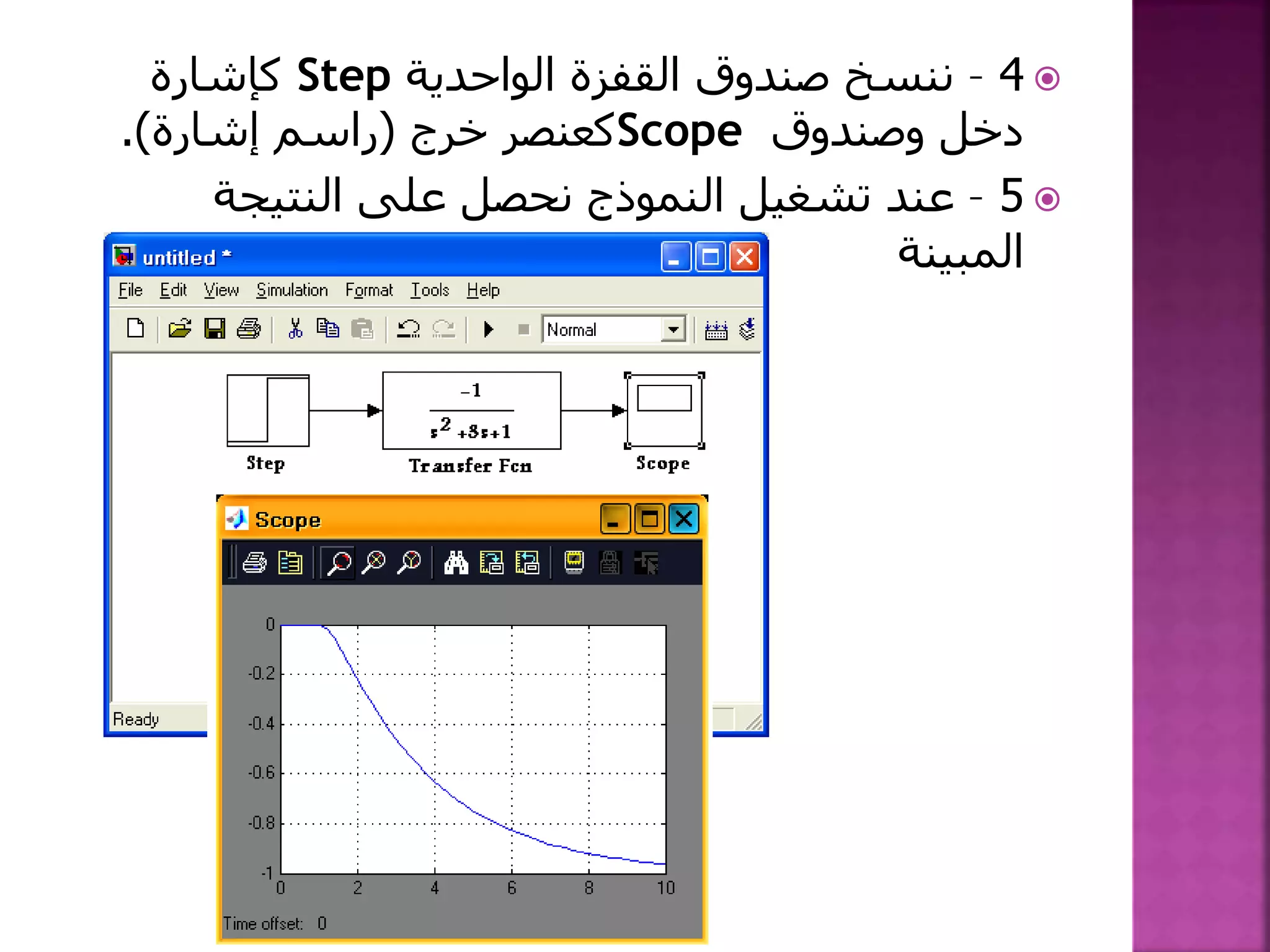
27. 1-‫نكتب‬ ‫أن‬ ‫يمكن‬ ‫الدارة‬ ‫من‬:
2–‫صند‬ ‫إليها‬ ‫وننسخ‬ ‫جديدة‬ ‫موديل‬ ‫نافذة‬ ‫نفتح‬‫وق‬
‫النقل‬ ‫تابع‬Transfer Fcn.
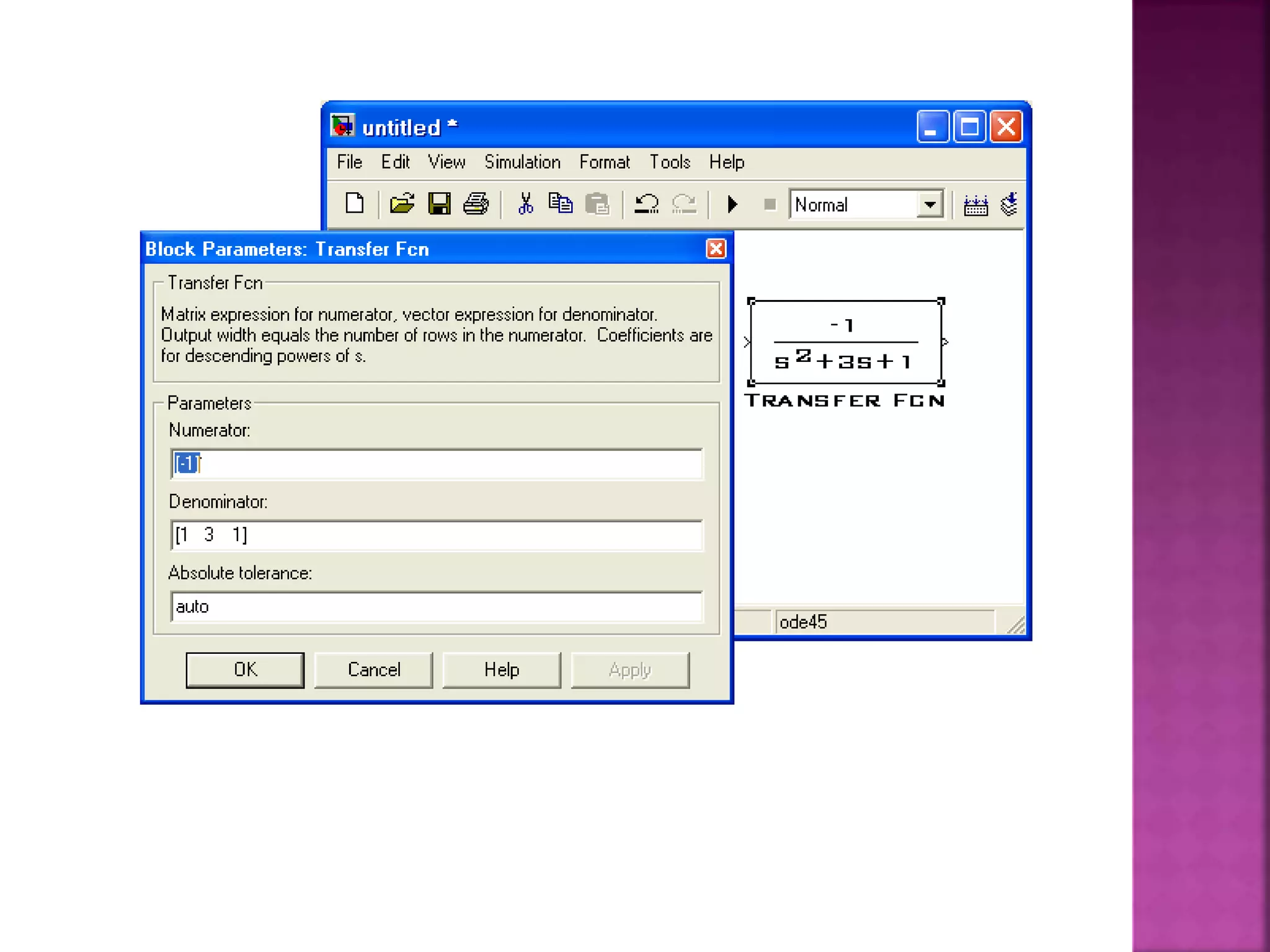
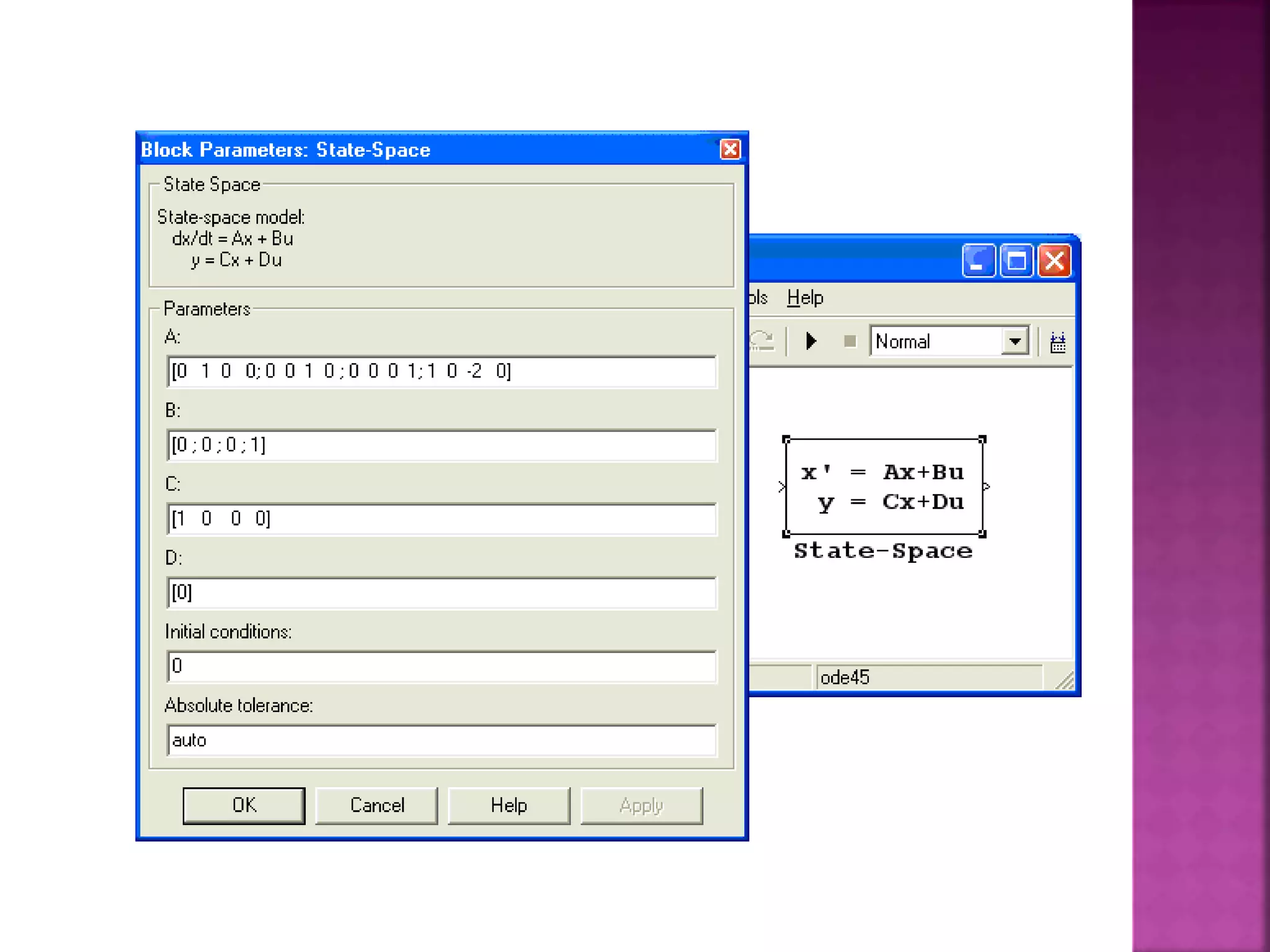
3–‫نافذة‬ ‫لفتح‬ ‫النقل‬ ‫تابع‬ ‫صندوق‬ ‫على‬ ‫ننقر‬
‫النقل‬ ‫تابع‬ ‫محددات‬ ‫إلدخال‬ ‫وذلك‬ ‫خصائصه‬.
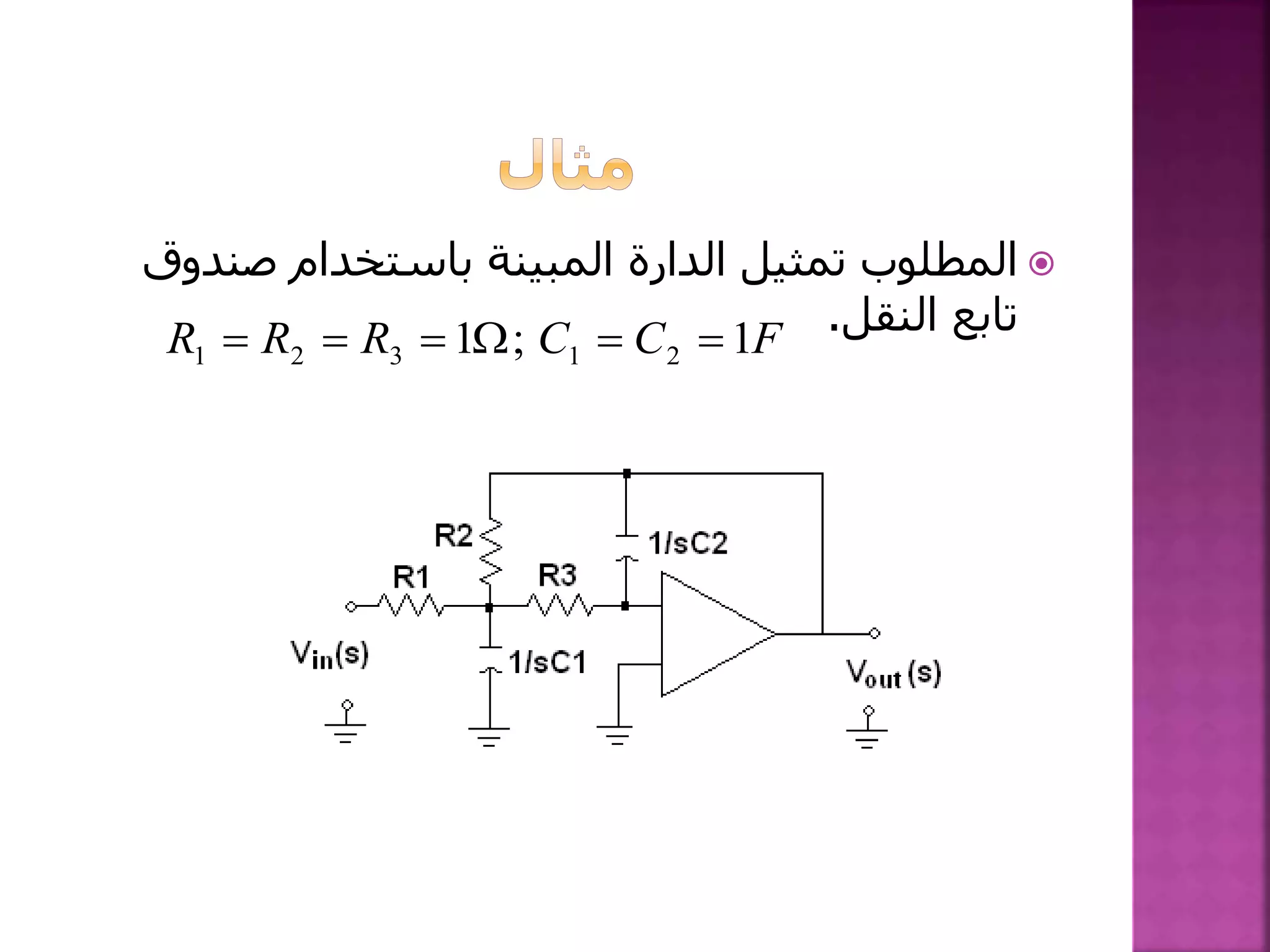
]/1))(/1/1/1[(
1
)(
)(
)(
22313211 RCsRsCRRRRSV
SV
sG
in
out



)13(
1
)(
)(
)( 2



SSSV
SV
sG
in
out

29. 4–‫القفزة‬ ‫صندوق‬ ‫ننسخ‬‫الواحدية‬Step‫كإشارة‬
‫وصندوق‬ ‫دخل‬Scope‫خرج‬ ‫كعنصر‬(‫إشارة‬ ‫راسم‬.)
5–‫النتيجة‬ ‫على‬ ‫نحصل‬ ‫النموذج‬ ‫تشغيل‬ ‫عند‬
‫المبينة‬

30. ‫معطى‬ ‫النقل‬ ‫تابع‬ ‫كان‬ ‫إذا‬ ‫يستخدم‬ ‫الصندوق‬ ‫هذا‬
‫أصفار‬ ‫شكل‬ ‫على‬Zeros‫وأقطاب‬Poles‫وربح‬gain
.

31. –‫وأقطاب‬ ‫أصفار‬ ‫شكل‬ ‫على‬ ‫التابع‬ ‫أعطي‬ ‫إذا‬
‫هذا‬ ‫خصائص‬ ‫نافذة‬ ‫في‬ ‫المعطيات‬ ‫هذه‬ ‫وأدخلت‬
‫الموضحة‬ ‫الصندوق‬‫في‬ ‫كما‬ ‫الصندوق‬ ‫على‬ ‫نحصل‬
‫الشكل‬‫الموضح‬:

32. 2–‫أدخلت‬ ‫إذا‬‫األصفار‬‫نافذة‬ ‫من‬ ‫والربح‬ ‫واألقطاب‬
‫األوامر‬
‫الخصائص‬ ‫نافذة‬ ‫تعديل‬ ‫وتم‬

33. ‫الزمني‬ ‫التأخير‬ ‫لعناصر‬ ‫الفرعية‬ ‫المكتبة‬ ‫تحتوي‬‫عدة‬
‫وهي‬ ‫عناصر‬:
The Transport Delay Block‫ذو‬ ‫النقل‬ ‫صندوق‬
‫الزمني‬ ‫التأخير‬.
The variable Time Delay Block‫التأخير‬ ‫صندوق‬
‫المتغير‬ ‫الزمني‬.
The variable Transport Delay Block‫صندوق‬
‫المتغير‬ ‫الزمني‬ ‫التأخير‬ ‫ذو‬ ‫النقل‬.

34. ‫بمقدار‬ ‫دخله‬ ‫إشارة‬ ‫ظهور‬ ‫بتأخير‬ ‫يقوم‬ ‫العنصر‬ ‫هذا‬
‫الزمن‬ ‫من‬ ‫محدد‬.‫لتمثي‬ ‫استخدامه‬ ‫يمكن‬ ‫وبالتالي‬‫ل‬
‫الزمني‬ ‫التأخير‬ ‫ذات‬ ‫العناصر‬.‫ال‬ ‫القيم‬ ‫تقبل‬ ‫ال‬‫زمنية‬
‫تحدي‬ ‫يتم‬ ‫الذي‬ ‫الزمني‬ ‫التأخير‬ ‫لمقدار‬ ‫السالبة‬‫ده‬.
‫مقدا‬ ‫يكون‬ ‫أن‬ ‫يجب‬ ‫األفضل‬ ‫الدقة‬ ‫على‬ ‫وللحصول‬‫ر‬
‫الحساب‬ ‫خطوة‬ ‫من‬ ‫أكبر‬ ‫الزمني‬ ‫التأخير‬.

35. ‫اإلشارة‬ ‫نقل‬ ‫المطلوب‬‫الجيبية‬‫بتأخير‬ ‫التالية‬‫زمني‬
‫قدره‬1‫ثانية‬.
،‫قدره‬ ‫تردد‬ ‫ذات‬ ‫اإلشارة‬1‫راديان‬/‫ثا‬.
)sin(10)( ttV 

36. ‫الزمن‬ ‫التأخير‬ ‫ذو‬ ‫النقل‬ ‫عنصر‬ ‫خصائص‬ ‫نافذة‬ ‫من‬‫ي‬
‫المحدد‬ ‫الزمني‬ ‫التأخير‬ ‫مقدار‬ ‫نحدد‬1‫ثانية‬.

37. ‫قي‬ ‫تحديد‬ ‫خالله‬ ‫من‬ ‫يمكن‬ ‫إضافي‬ ‫مدخل‬ ‫يمتلك‬‫مة‬
‫الزمني‬ ‫التأخير‬

38. ‫حيث‬ ‫المتغير‬ ‫التأخير‬ ‫ذو‬ ‫النقل‬ ‫عنصر‬ ‫استخدام‬
‫إشارة‬ ‫لتأخير‬ ‫استخدم‬‫جيبية‬‫بتردد‬2‫راديان‬/‫ثانية‬
‫ومطال‬5‫بمقدار‬2‫ثانية‬.
‫الشكل‬ ‫على‬ ‫مبينة‬ ‫النتيجة‬