Recommended
PDF
第六回「データ解析のための統計モデリング入門」前半
PDF
データ解析のための統計モデリング入門3章後半
PDF
PDF
PPTX
PPTX
[The Elements of Statistical Learning]Chapter8: Model Inferennce and Averaging
PDF
DARM勉強会第3回 (missing data analysis)
PDF
PPT
PDF
PDF
ガウス過程回帰の導出 ( GPR : Gaussian Process Regression )
PDF
PPTX
PDF
PDF
PDF
【Zansa】第12回勉強会 -PRMLからベイズの世界へ
PPTX
PPTX
PPTX
PDF
PDF
[読会]Logistic regression models for aggregated data
PPTX
PDF
ビジネス活用事例で学ぶデータサイエンス入門 #2
PPTX
[The Elements of Statistical Learning]Chapter18: High Dimensional Problems
PDF
PDF
[読会]A critical review of lasso and its derivatives for variable selection und...
PDF
PDF
PDF
PDF
More Related Content
PDF
第六回「データ解析のための統計モデリング入門」前半
PDF
データ解析のための統計モデリング入門3章後半
PDF
PDF
PPTX
PPTX
[The Elements of Statistical Learning]Chapter8: Model Inferennce and Averaging
PDF
DARM勉強会第3回 (missing data analysis)
PDF
What's hot
PPT
PDF
PDF
ガウス過程回帰の導出 ( GPR : Gaussian Process Regression )
PDF
PPTX
PDF
PDF
PDF
【Zansa】第12回勉強会 -PRMLからベイズの世界へ
PPTX
PPTX
PPTX
PDF
PDF
[読会]Logistic regression models for aggregated data
PPTX
PDF
ビジネス活用事例で学ぶデータサイエンス入門 #2
PPTX
[The Elements of Statistical Learning]Chapter18: High Dimensional Problems
PDF
PDF
[読会]A critical review of lasso and its derivatives for variable selection und...
PDF
PDF
Similar to データ解析のための統計モデリング入門 6.5章 後半
PDF
PDF
PDF
一般化線形モデル (GLM) & 一般化加法モデル(GAM)
PPTX
PDF
分割表の作図・GLM・ベイズモデル http://goo.gl/qQ1Ok
PDF
MLaPP 9章 「一般化線形モデルと指数型分布族」
PDF
PDF
PDF
PDF
Infomation geometry(overview)
PDF
PRML_titech 2.3.1 - 2.3.7
PDF
PDF
PDF
[PRML] パターン認識と機械学習(第1章:序論)
PPTX
PPTX
NagoyaStat #5 データ解析のための
統計モデリング入門 第10章
PDF
PDF
PPTX
PDF
[PRML] パターン認識と機械学習(第2章:確率分布)
データ解析のための統計モデリング入門 6.5章 後半 1. 2. 3. 6章 GLMの応用範囲 後半
3
章 適用例 確率分布 リンク関数 ポイント
前半 生存確率の予測 二項分布 logit
6.5 生存確率の予測 二項分布 logit 交互作用項
6.6 人口密度の予測 ポアソン 対数リンク オフセット
6.7 連続値データ 正規分布 ̶̶
連続値の
最尤推定
6.8
確率変数が
0以上の連続値
ガンマ分布 対数リンク GLMすごい
6.9 ま と め
4. 6章 GLMの応用範囲 後半
4
章 適用例 確率分布 リンク関数 ポイント
前半 生存確率の予測 二項分布 logit
6.5 生存確率の予測 二項分布 logit 交互作用項
6.6 人口密度の予測 ポアソン 対数リンク オフセット
6.7 連続値データ 正規分布 ̶̶
連続値の
最尤推定
6.8
確率変数が
0以上の連続値
ガンマ分布 対数リンク GLMすごい
6.9 ま と め
5. 6. 7. 7
交互作用項を含めたGLM
glm(cbind(y, N-y)~ x * f, family = binomial, data = d)
または
glm(cbind(y,N-y)~x + f + x:f, family=binomial, data=d)
Coefficients:
(Intercept) x fT x:fT
-18.52332 1.85251 -0.06376 0.21634
!
Degrees of Freedom: 99 Total (i.e. Null); 96 Residual
Null Deviance: 499.2
Residual Deviance: 122.4 AIC: 273.6
8. 8
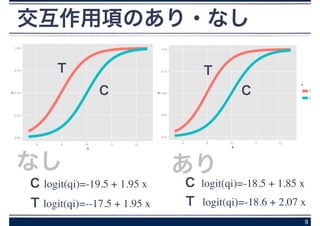
交互作用項のあり・なし
Coefficients:
(Intercept) x fT
-19.536 1.952 2.022
!
Degrees of Freedom: 99 Total (i.e. Null); 97 Residual
Null Deviance: 499.2
Residual Deviance: 123 AIC: 272.2
Coefficients:
(Intercept) x fT x:fT
-18.52332 1.85251 -0.06376 0.21634
!
Degrees of Freedom: 99 Total (i.e. Null); 96 Residual
Null Deviance: 499.2
Residual Deviance: 122.4 AIC: 273.6
あり
なし
9. 10. 10
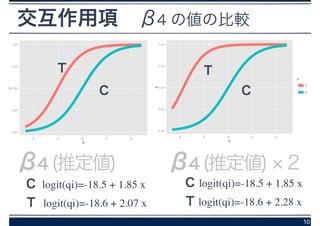
交互作用項 β4 の値の比較
β4 (推定値)
T
C C
T
C logit(qi)=-18.5 + 1.85 x
T logit(qi)=-18.6 + 2.28 x
β4 (推定値) 2
C logit(qi)=-18.5 + 1.85 x
T logit(qi)=-18.6 + 2.07 x
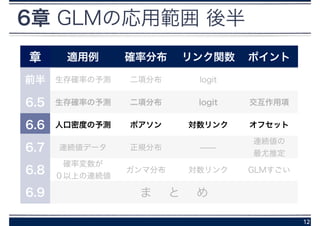
11. 12. 6章 GLMの応用範囲 後半
12
章 適用例 確率分布 リンク関数 ポイント
前半 生存確率の予測 二項分布 logit
6.5 生存確率の予測 二項分布 logit 交互作用項
6.6 人口密度の予測 ポアソン 対数リンク オフセット
6.7 連続値データ 正規分布 ̶̶
連続値の
最尤推定
6.8
確率変数が
0以上の連続値
ガンマ分布 対数リンク GLMすごい
6.9 ま と め
13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 6章 GLMの応用範囲 後半
22
章 適用例 確率分布 リンク関数 ポイント
前半 生存確率の予測 二項分布 logit
6.5 生存確率の予測 二項分布 logit 交互作用項
6.6 人口密度の予測 ポアソン 対数リンク オフセット
6.7 連続値データ 正規分布 ̶̶
連続値の
最尤推定
6.8
確率変数が
0以上の連続値
ガンマ分布 対数リンク GLMすごい
6.9 ま と め
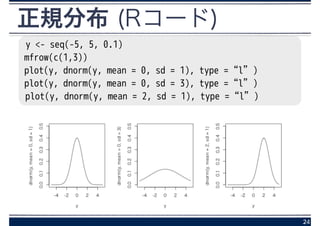
23. 24. 正規分布 (Rコード)
24
y <- seq(-5, 5, 0.1)
mfrow(c(1,3))
plot(y, dnorm(y, mean = 0, sd = 1), type =“l”)
plot(y, dnorm(y, mean = 0, sd = 3), type =“l”)
plot(y, dnorm(y, mean = 2, sd = 1), type =“l”)
25. 26. 27. 28. 29. 6章 GLMの応用範囲 後半
29
章 適用例 確率分布 リンク関数 ポイント
前半 生存確率の予測 二項分布 logit
6.5 生存確率の予測 二項分布 logit 交互作用項
6.6 人口密度の予測 ポアソン 対数リンク オフセット
6.7 連続値データ 正規分布 ̶̶
連続値の
最尤推定
6.8
確率変数が
0以上の連続値
ガンマ分布 対数リンク GLMすごい
6.9 ま と め
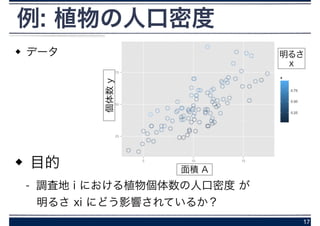
30. 31. 例 花と葉っぱ
花の重量 yi と葉の重量 xi の関係
- 花の重量 yi が平均 μi のガンマ分布に従うとする
平均花重量μi のモデル
- 葉重量x_i の単調増加関数
31
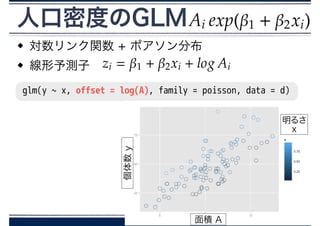
32. 33. ガンマ分布のGLM
対数リンク関数 + ガンマ分布
線形予測子
33
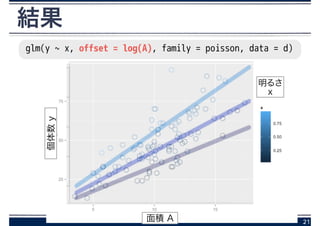
glm(y ~ log(x), family = Gamma(link=“log”),data = d)
Coefficients:
(Intercept) log(x)
-1.0403 0.6833
!
Degrees of Freedom: 49 Total (i.e. Null); 48 Residual
Null Deviance: 35.37
Residual Deviance: 17.25 AIC: -110.9
34. 6章 GLMの応用範囲 後半
34
章 適用例 確率分布 リンク関数 ポイント
前半 生存確率の予測 二項分布 logit
6.5 生存確率の予測 二項分布 logit 交互作用項
6.6 人口密度の予測 ポアソン 対数リンク オフセット
6.7 連続値データ 正規分布 ̶̶
連続値の
最尤推定
6.8
確率変数が
0以上の連続値
ガンマ分布 対数リンク GLMすごい
6.9 ま と め
35. 6章 GLMの応用範囲 後半
35
章 適用例 確率分布 リンク関数 ポイント
前半 生存確率の予測 二項分布 logit
6.5 生存確率の予測 二項分布 logit 交互作用項
6.6 人口密度の予測 ポアソン 対数リンク オフセット
6.7 連続値データ 正規分布 ̶̶
連続値の
最尤推定
6.8
確率変数が
0以上の連続値
ガンマ分布 対数リンク GLMすごい
6.9 ↑ この表 ↑
36.

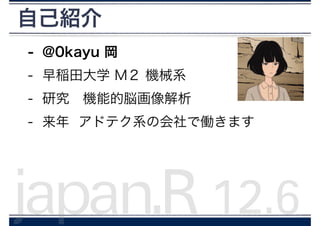














![正規分布の確率
25
> pnorm(1.8, 0, 1) - pnorm(1.2, 0, 1)
[1] 0.07914
!
> dnorm(1.5, 0, 1) * 0.6
[1] 0.07771
確率 = 確率密度関数 Δy](https://image.slidesharecdn.com/midoribon6-140729055844-phpapp01/85/6-5-25-320.jpg)