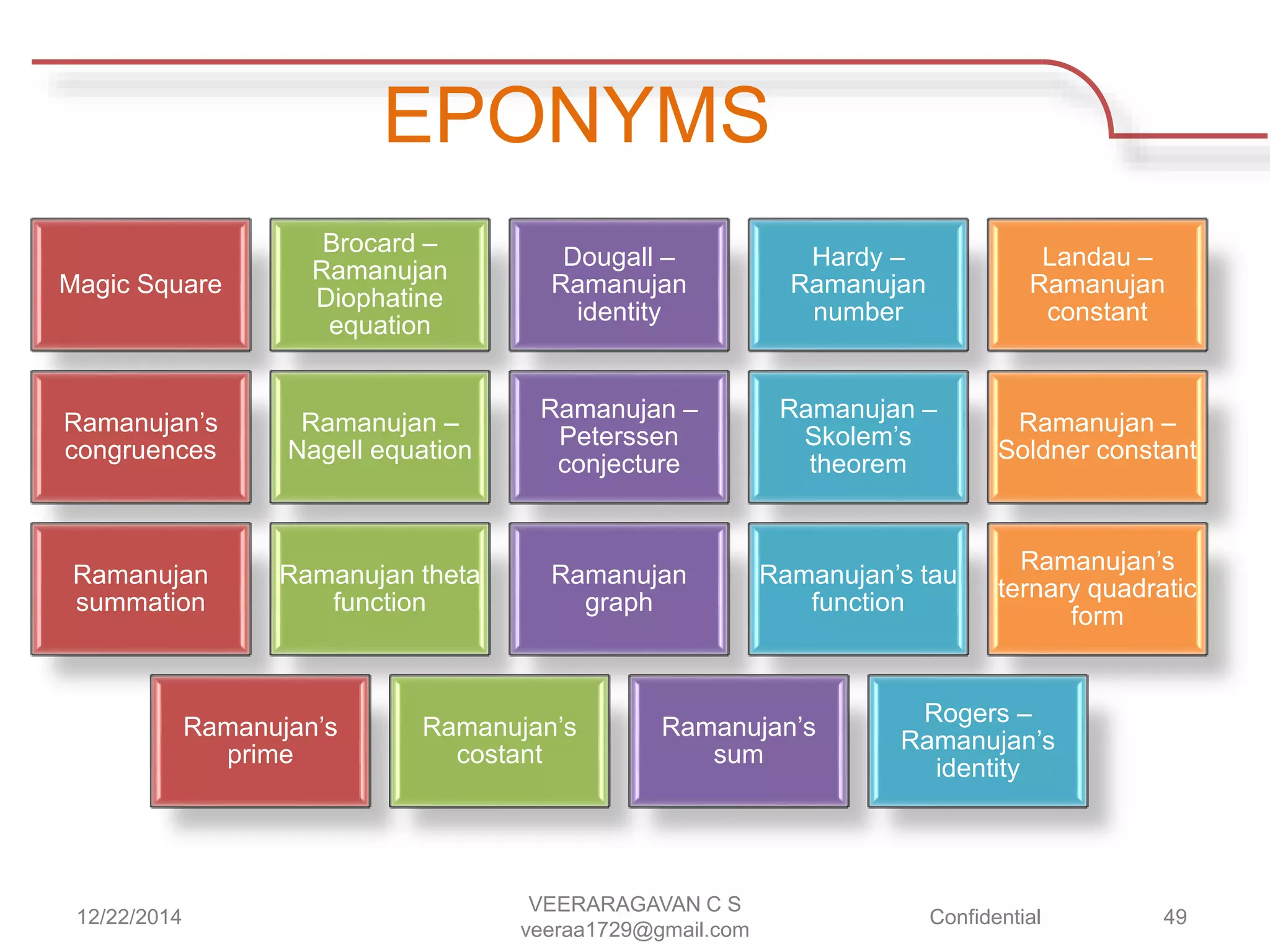
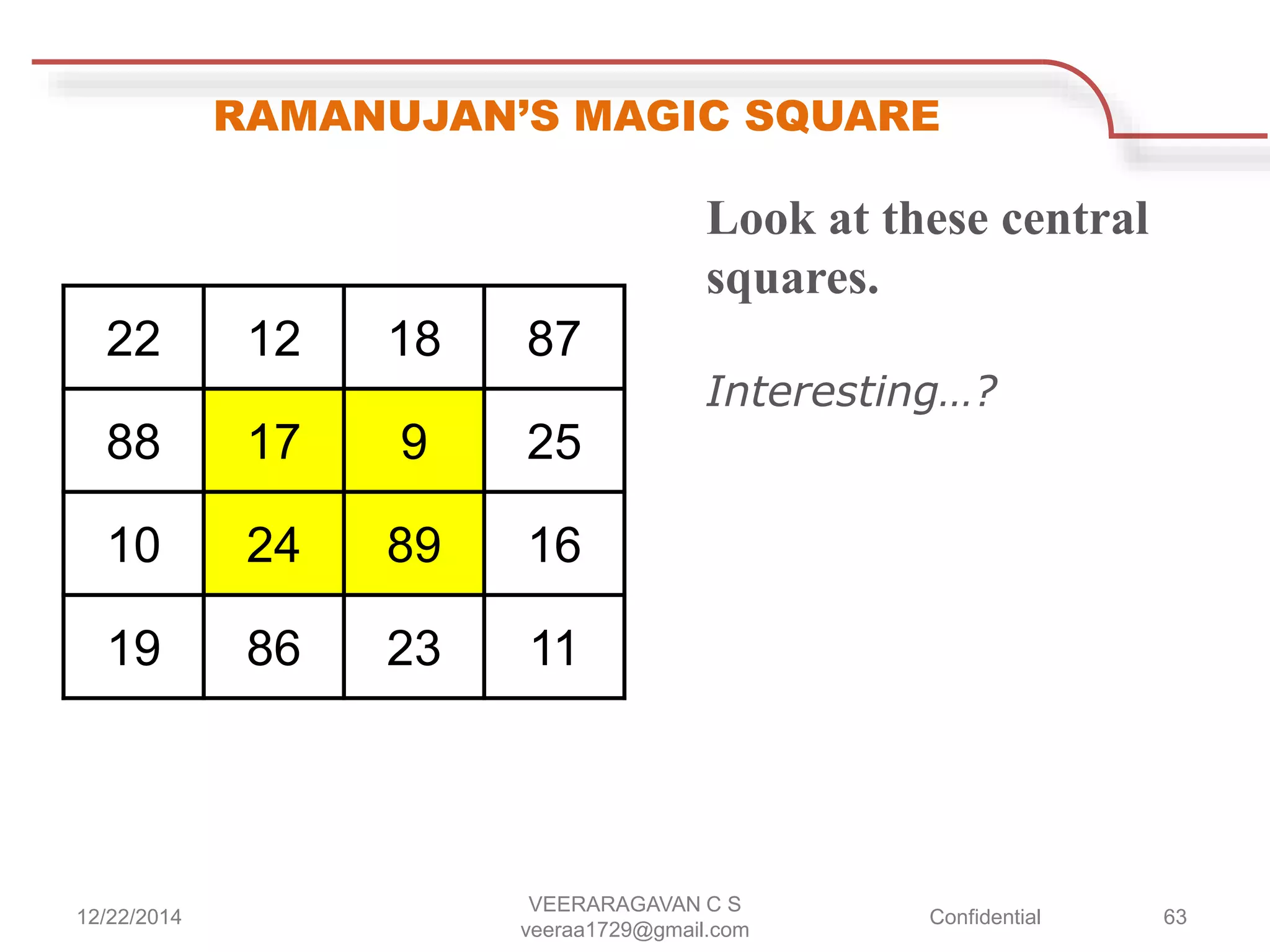
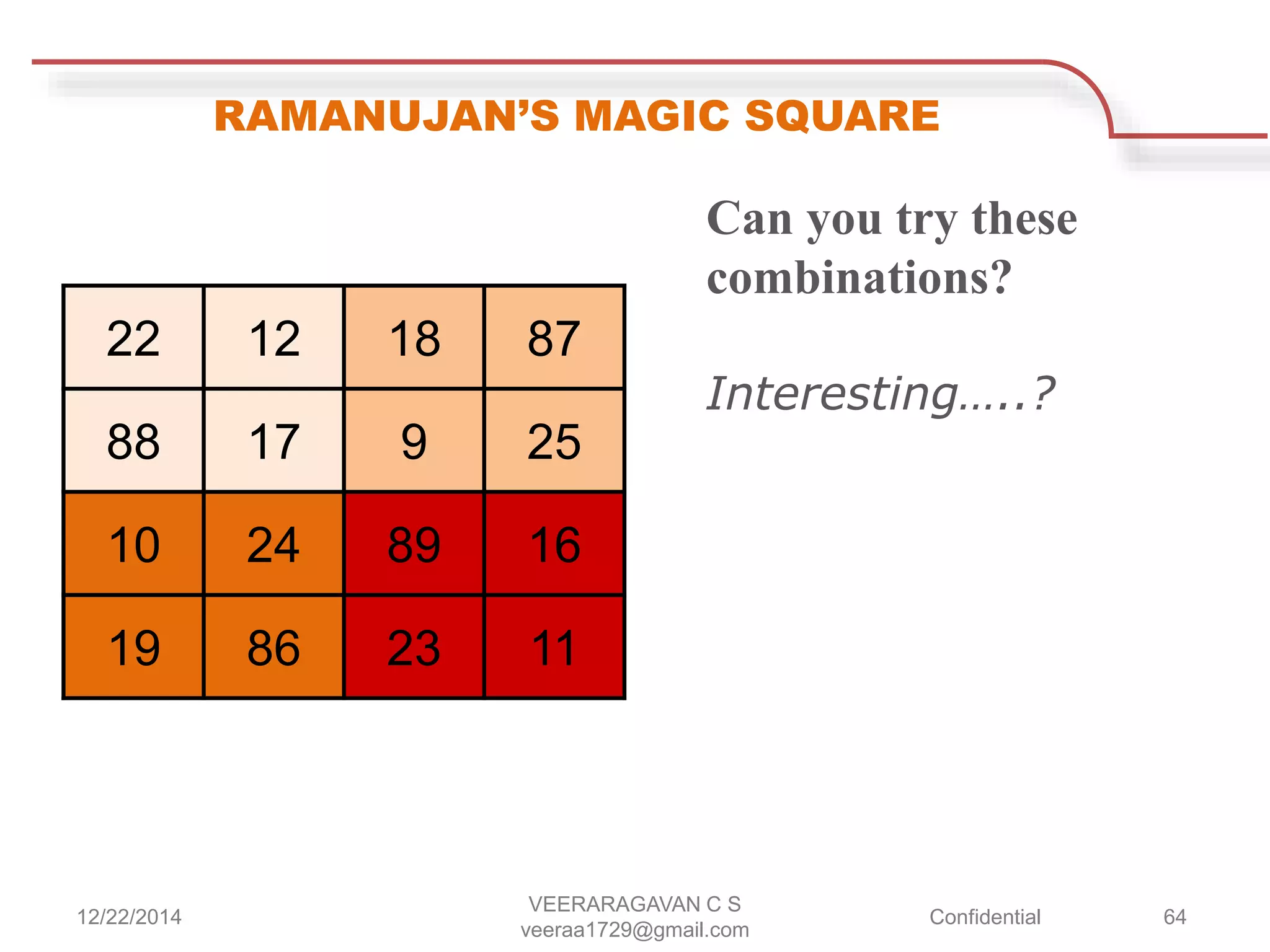
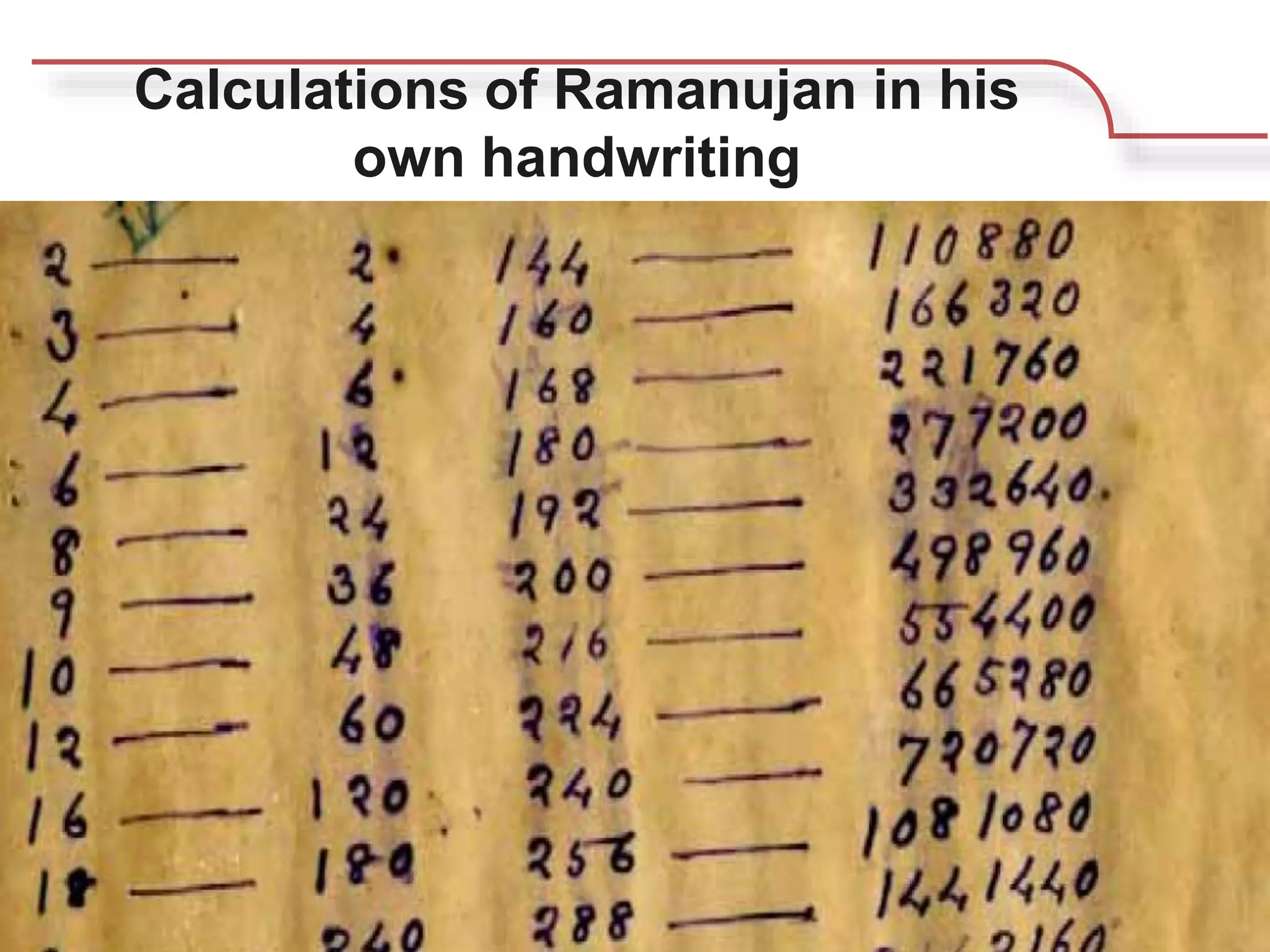
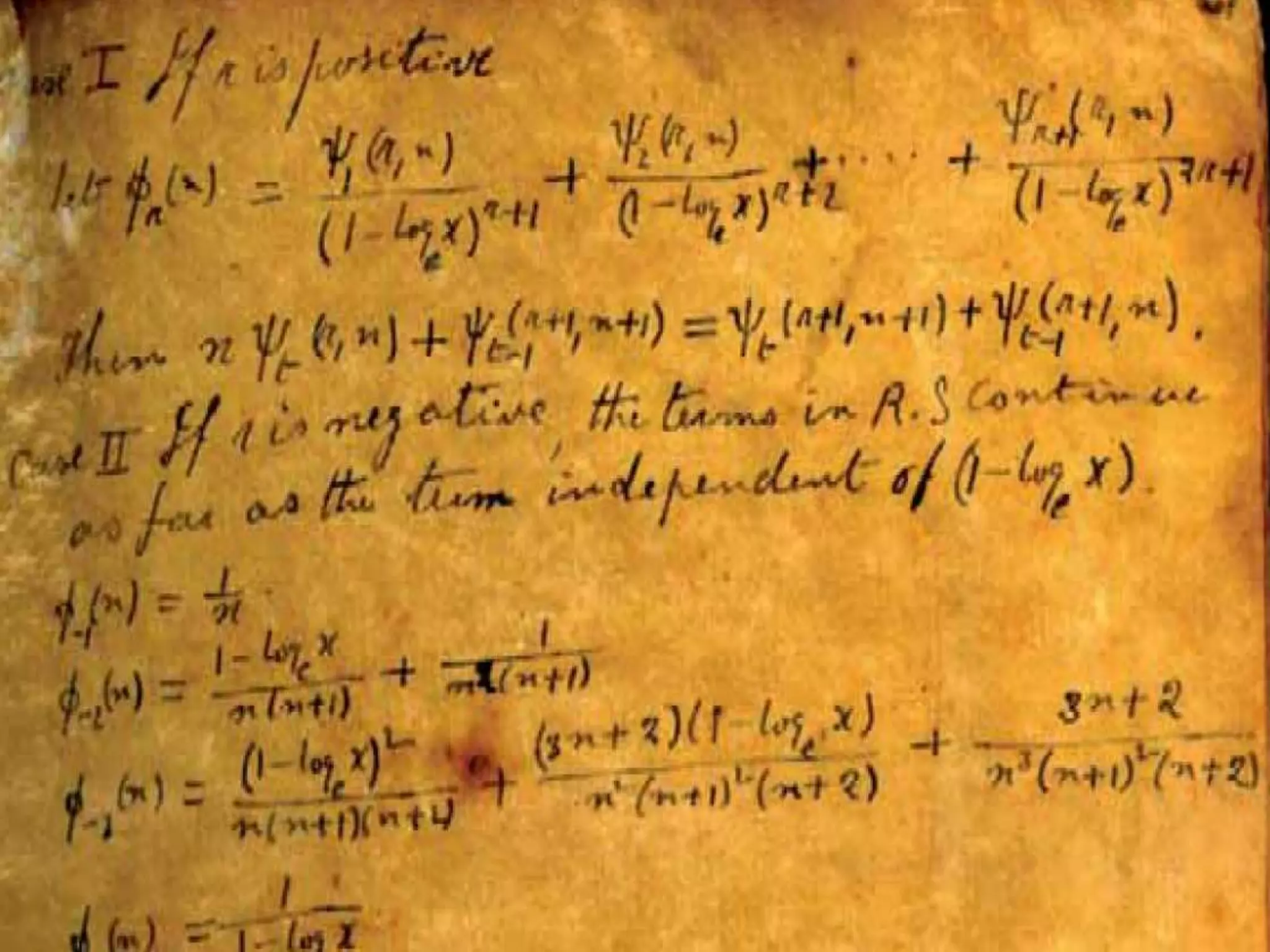Srinivasaramanujan a reminiscence 3

SRINIVASA RAMANUJAN’S
LIFE AND HIS GENIUS
1887-1920

CONTENT
• Prodigy (5 – 8)Child
• Life Downs & Ups (9 – 14)Struggle
• Acquaintance with Prof.G.H.Hardy (15 – 20)Hardy
• Properties of Taxicab number ( 21 )1729
• Misperception (22,23)View
• Family life (24 – 29)Personal
• To him (30 – 32)God
• Quotes about Ramanujan (33 – 41)Quotes
• Ramanujan Eponyms (42, 43)Eponyms
• Lessons learnt / unlearnt (44 – 48)Lessons
• Ramanujan and Magic Square (49 – 76)Magic Squares
• References / Further Readings (77 – 79)References 12/22/2014
VEERARAGAVAN C S VEERAA1729@GMAIL.COM

SRINIVASA RAMANUJAN
Born - 22 December 1887
Kumbakonam, Madras Presidency
British India
Died - 26 April 1920
Chetput, Madras, British India
College - Government Arts College
Pachaiyappa’s College
Cambridge University
Academic Advisors - G.H.Hardy
J.E.Littlewood 12/22/2014VEERARAGAVAN C S VEERAA1729@GMAIL.COM
4

CHILD PRODIGY
 Learned college level mathematics by age 11
 Bernoulli numbers by age 13 (rediscovering Euler’s
identity)
 While in school, he was gifted George Schoobridge
Carr’s Synopsis of Pure and Applied Mathematics.
 This book listed 4865 formulae in algebra,
trigonometry, analytical geometry and calculus
without proof.
 Ramanujan not only proved himself each but derived
many new results and recorded them.
12/22/2014VEERARAGAVAN C S VEERAA1729@GMAIL.COM
JACOB
1655-1705
JOHANN
1667-1748
NICOLAUS I
1687-1759
NICOLAUS II
1695-1726
DANIEL
1700-1782
JOHANN Ii
1710-1790
JOHANN III
1744-1807
JACOB II
1759-1789

A THOUGHT OF A 7 YEAR OLD
 Teacher:
n
n
= 1, for every integer n.
 Ramanujan: “Is zero divided by zero is also one?”
 Teacher : ??????
 Ramanujan’s Explanation !
 “Zero divided by zero may be anything.
 The zero of the numerator may be several times the zero
of the denominator and vice versa”.
 (Thinking of limits and limiting process)
6
Which
number is
greater than
infinity?

EARLY LIFE
 Born in Erode to K. Srinivasa Iyengar and
Komalathammal
 Lived in Sarangapani Street in Kumbakonam
 Went school first on 1.10.1892.
 Had to switch primary school 3 times due to
circumstances.
 Completed Math exam in half the allotted time.
 Stood District First at Kumbakonam High School
(1898)
 Carr’s synopsis of Elementary Results in Pure and
Applied Mathematics. Book acknowledged in
awakening the genius of Ramanujan.
 Left college without a degree and pursued research in
Mathematics.
12/22/2014VEERARAGAVAN C S VEERAA1729@GMAIL.COM7

ADULTHOOD IN INDIA
 After High school, he passed a competitive exam
in English & Maths and secured the Scholarship.
 Due to his preoccupation with Maths, he could
not pass in English & Sanskrit and not promoted
to Senior F.A. Class and lost Scholarship
 Married to a 9 year old bride Janaki Ammal on 14
July 1909
 Went door to door for job from 18 to age 24.
 Tutored college students

ATTENTION FROM MATHEMATICIANS
 Met V. Ramaswamy Aiyer, founder of Indian
Mathematical Society
 “I was struck by the extraordinary mathematical results
contained in it [the notebooks]. I had no mind to
smother his genius by an appointment in the lowest
rungs of the revenue department”
 Introduced to R. Ramachandra Rao, secretary of the
Indian Mathematical Society
 Impressed by Ramanujan but doubted his integrity.
 Continued Mathematical Research with Rao’s financial
help

22-12-2014
VEERARAGAVAN C S, APTITUDE
TRAINER, veeraa1729@gmail.com 12
N
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
Eg: P = 1000, R=10 %, and N=3 years.
What is CI & Amount?
Step 1:
10% of 1000 = 100.
10% of 100 = 10
10% of 10 = 1
Since n = 3, three times calculation.
Step 2:
Amount after 3 years
= 1 * 1000 + 3 * 100 + 3 * 10 + 1 * 1
= Rs.1331
Step 3:
CI after 3 years = 3*100 + 3*10 + 1*1
= Rs.331
(leaving out first term in step 2).
1 2 1
ஒரு
பேருந்தி
யிருமலர்
தவிசில்
ஒருமுறை
அயறை
யீன்ைறை
1 2 3 2 1
ஒரு
முறை
இரு சுடர்
மீதிைிலியங்கா
மும்மதில்
இலங்றக
யிரு கால்
வறைய
ஒருசிறல
1 2 3 4 3 2 1
ஒன்ைிய ஈரெயிற்ைழல்வா
ய் வாைியில்
அட்டறை
மூவடி நாைிலம்
பவண்டி
முப்புரிரலாடு
மானுரி
யிலங்கும்
மார்விைில்

FIRST CONTRIBUTION
 Published his work in Journal of Indian Mathematical
Society at the age of 23, first full paper (15 pages) on
“Some properties of Bernoulli Numbers”.
 First problem which he posed
 He then formulated an equation to solve the infinitely
nested radicals problem.
 Wrote his 1st formal paper for the journal on the
properties of Bernoulli Numbers

1 + 2 1 + 3 1 + ⋯ . RAMANUJAN HIMSELF
SUPPLIED THE SOLUTION TO THIS PROBLEM
3 = 9
= 1 + 8
= 1 + 2 ∗ 4
= 1 + 2 16
= 1 + 2 1 + 15
= 1 + 2 1 + 3 ∗ 5
= 1 + 2 1 + 3 25
= 1 + 2 1 + 3 1 + 24
= 1 + 2 1 + 3 1 + 4 ∗ 6
=
1 + 2 1 + 3 1 + 4 36
= 1 + 2 1 + 3 1 + ⋯ .

WORK
 In early 1912 he got a job in the Madras
Accountant Generals office with a salary of Rs 20
per month.
 Later he applied for a position under the Chief
Accountant of the Madras Port Trust
 Accepted as a Class III, Grade IV accounting clerk
making 30 rupees per month
 Spent spare time doing Mathematical Research

INTRODUCTION WITH
G.H.HARDY
 G.H. Hardy was an academician at Cambridge University
 He was a prominent English mathematician, known for his
achievements in number theory and mathematical analysis.
 Later on Ramanujan wrote to G.H.Hardy
 Hardy recognised some of his formulae but other “seemed
scarcely possible to believe”. Some of them were –
Relating to infinite series -

RECOGNITION OF HIS
GENIUS
 Initially, G. H. Hardy thought that the works of
Ramanujan were fraud because most of them were
impossible to believe.
 But eventually ,he was convinced and interested in his
talent.

G.H.HARDY’S RECOGNITION
 Hardy invited Ramanujan to Cambridge University but
Ramanujan refused.
 Hardy then enlisted E.H.Neville to bring him to
England.
 With his parents supporting him he agreed this time.

CONTACTING ENGLISH
MATHEMATICIANS
 M. J. M. Hill of University College London
argued that though Ramanujan had taste for
Mathematics he lacked the proper educational
background and foundation
 He refused to take Ramanujan as student
 But gave him professional advice on his work

CALCULUS &
NUMBER
THEORY

LIFE IN
ENGLAND
 Ramanujan boarded the S.S.Nevasa on 17 March 1914
and arrived in London on 14th April
 Ramanujan began working with Hardy and Littlewood
 Hardy received 120 theorems from him in 1st 2 letters but
there were many more results in his notebook
 Ramanujan spent nearly 5 years in Cambridge
 Ramanujan was awarded the B.A degree by Research in
March 1916 at an age of 28 years for his work on Highly
Composite Numbers.

LIFE IN ENGLAND
 He was elected a Fellow of the Royal Society of
London in February 1918 at an age of 30 years.
 He was the second Indian to become FRS.( First one
was in 1841).
 He was elected to a Trinity College Fellowship as the
FIRST INDIAN.
 During his five years stay in Cambridge he published
twenty one research papers containing theorems.
The first Indian
citizen to be
elected to the
Fellowship of the
Royal Society
was Ardaseer
Cursetjee.
He was part of the
same
industrialisation
processes which
inspired the GTS,
introducing both
gas lighting and
steam pumps to his
native town of
Bombay.
The Royal Society
and India | Royal
Society
https://royalsociet
y.org/exhibitions/20
07/india/

RAMANUJAN - HARDY NUMBER
1729
 Hardy arrived in a cab numbered 1729
 He commented that the number was uninteresting or dull.
 Instantly Ramanujan claimed that it was the smallest natural
number which can be written as sum of cubes in 2 ways
 1729 = 13 + 123 = 93 + 103
 1729 = 7 x 13 x 19 product of primes in A.P
 1729 divisible by its sum of digits.
 1729 = 19 x 91
 1729 is a sandwich number or HARSHAD number. 12/22/2014VEERARAGAVAN C S VEERAA1729@GMAIL.COM24

TAXICAB NUMBERS

MISPERCEPTIONS
 Ramanujan recorded the bulk of his results in four
notebooks of loose leaf paper (About 4000 theorems)
 These results written up without any derivations.
 Since paper was very expensive, He would do most of his
work (derivations) on SLATE and transfer just the results to
paper.
 Hence the perception that he was unable to prove his
results and simply thought up the final result directly is
NOT CORRECT

MISPERCEPTION
 Professor Bruce C.Berndt of University of
Illinois, who worked on Ramanujan note
books, stated that “Over the last 40 years,
nearly all of Ramanujan’s theorems have
been proven right”.
 Also Mathematicians agreed unanimously on
the point that it was not possible for someone
to imagine those results without solving /
proving.

ILLNESS & RETURN TO INDIA
 Ramanujan's health worsened in England
 Diagnosed with Tuberculosis and Vitamin
deficiency
 Returned to Kumbakonam in 1919 and died
soon thereafter at the age of 32
 In 1994 Dr. D.A.B. Young analysed his records
and concluded he had hepatic amoebiasis

RAMANUJAN’S NOTEBOOKS
 Recorded his work in 4 notebooks of loose leaf paper
 Results were written without derivation
 Mathematician Bruce C. Berndt says that Ramanujan
was able to make the proofs but chose not to.
 Might have worked on slate
 Or may be influenced by G.S Carr’s book which stated
results without proofs
 Mathematicians such as Hardy, G.N. Watson, B.M.
Wilson and Bruce Berndt created papers from his work

OTHER MATHEMATICIANS’ VIEWS
OF RAMANUJAN
 J.H. Hardy was highly impressed by Ramanujan
 Hardy said that the solutions were "arrived at by a process
of mingled argument, intuition, and induction, of which he
was entirely unable to give any coherent account”
 On the basis of pure talent
 Hardy rated himself a score of 25 out of 100,
 J.E. Littlewood 30, David Hilbert 80 and
 Ramanujan 100 !
 Physicist Jayant Narlikar appreciated Ramanujan’s
discoveries 12/22/2014VEERARAGAVAN C S VEERAA1729@GMAIL.COM32

RECOGNITION
 Tamil Nadu celebrates 22 December as ‘State IT
Day’
 Stamp released by the Govt. in 1962
 22nd December celebrated as Ramanujan Day in
Govt Arts College, Kumbakonam
 National Symposium On Mathematical Methods
and Applications (NSMMA)
 SASTRA Ramanujan Prize

IN POPULAR CULTURE
A play ‘First Class Man’ is centered around Ramanujan
Book by Robert Kanigel titled ‘The Man Who Knew Infinity: A Life
of the Genius Ramanujan’ is his biography
In the famous film ‘Good Will Hunting’ the main character is
compared to Ramanujan
‘A Disappearing Number’, a show by British Stage Production is
about Ramanujan and Hardy
Character Amita Ramanujan in the show Numb3rs is named after
him
Roger Spottiswoode is working on a movie on mathematical genius
Srinivasa Ramanujan starring Rang De Basanti actor Siddharth.
Titled The First Class Man, the film's scripting has been completed
and shooting is being planned .

PERSONALITY AND SPIRITUAL LIFE
 A person with a somewhat shy and quiet disposition
 A dignified man with pleasant manners
 Ramanujan credited his success to his family Goddess,
Namagiri of Namakkal
 He claimed to receive visions of scrolls of complex
mathematical content unfolding before his eyes
 "An equation for me has no meaning, unless it represents a
thought of God.”

SPRITUALITY
 For example, 2n – 1 will denote the primordial GOD.
 When n is zero, the expression denotes ZERO.
 He spoke of “ZERO” as the symbol of the absolute (Nirguna
– Brahmam) of the extreme monistic school of philosophy)
 The reality to which no qualities can be attributed, which no
qualities can be a
 When n is 1, it denotes UNITY, the Infinite GOD.
 When n is 2, it denotes TRINITY.
 When n is 3, it denotes SAPTHA RISHIS and so on.

SPRITUALITY
 He looked “infinity” as the totality of all possibilities which was
capable of becoming manifest in reality and which was
inexhaustible.
 According to Ramanujan, The product of infinity and zero would
supply the whole set of finite numbers.
 Each act of creation, could be symbolized as a particular product
of infinity and zero, and from each product would emerge a
particular individual of which the appropriate symbol was a
particular finite number.
 As narrated by Prof.Prasantha Chandra, Statistician,
contemporary and good friend of Ramanujan at Cambridge.

QUOTES
PROF. RICHARD ASKEY –
UNIVERSITY OF WISCONSIN - MADISON
 “Try to imagine the quality of Ramanujan’s mind, one
which drove him to work unceasingly while deathly ill,
and one great enough to grow deeper while his body
became weaker.
 I stand in awe of his accomplishments; understanding
is beyond me.
 We would admire any mathematician whose life’s work
was half of what Ramanujan found in the last year of
his life while he was dying”.

BRUCE C BERNDT
PROFESSOR, UNIVERSITY OF ILLINOIS
 Hardy’s personal ratings of mathematicians:
 Suppose that we rate mathematicians on the
basis of pure talent on a scale from 0 to 100.
 Hardy gave himself a score of 25,
 Littlewood 30,
 Hilbert 80 and Ramanujan 100

ROBERT KANIGEL
AUTHOR OF “THE MAN WHO KNEW INFINITY:
A LIFE OF THE GENIUS RAMANUJAN”
 Sheer intuitive brilliance coupled to long, hard hours
on his slate made up for most of his educational
lapse.
 This ‘poor and solitary Hindu pitting his brains
against the accumulated wisdom of Europe’ as
Hardy called him, had rediscovered a century of
mathematics and
 Made new discoveries that would captivate
mathematicians for next century.

S.CHANDRASEKHAR
INDIAN ASTROPHYSICIST,
NOBEL LAUREATE 1983
 “I think it is fair to say that almost all the
mathematicians who reached distinction
during the three or four decades following
Ramanujan were directly or indirectly inspired
by his example.
 Even those who do not know about
Ramanujan’s work are bound to be fascinated
by his life.”

S.CHANDRASEKHAR
INDIAN ASTROPHYSICIST,
NOBEL LAUREATE 1983
 “The fact that Ramanujan’s early years were spent in a
scientifically sterile atmosphere,
 that his life in India was not without hardships that under
circumstances that appeared to most Indians as nothing
short of miraculous,
 He had gone to Cambridge, supported by eminent
mathematicians, and
 Had returned to India with very assurance that he would be
considered,
 in time as one of the most original mathematicians of the
century.

PROF. HARDY
 “I have to form myself, as I have never really formed before
and try to help you to form, some of the reasoned estimate
of the most romantic figure in the recent history of
mathematics,
 a man whose career seems full of paradoxes and
contradictions,
 who defies all cannons by which we are accustomed to
judge one another and
 about whom all of us will probably agree in one judgement
only,
 that he was in some sense a very great mathematician.”

BERTRAND ARTHUR WILLIAM RUSSELL
BRITISH PHILOSOPHER & MATHEMATICIAN,
NOBEL LAUREATE
 I found Hardy and Littlewood in a state
of wild excitement because they believe,
they have discovered a second Newton,
 A Hindu Clerk in Madras… He wrote to
Hardy telling of some results he has got,
which Hardy thinks quite wonderful.”

PROF. ATLE SELBERG
NORWEGIAN MATHEMATICIAN
 “Ramanujan’s conjectures formulated and their later
generalization, have come to play a more central role
in the mathematics of today, serving as a kind of focus
for the attention of quite a large group of the best
mathematicians of our time.
 The estimates of Ramanujan’s nature in mathematics
certainly have been growing over the years.
 There is no doubt about that.”

PROF.JAYANT NARLIKAR
INDIAN ASTROPHYSICIST
IN HIS BOOK SCIENTIC EDGE
 S.Ramanujan, discovered by the Cambridge
mathematician Hardy, whose great mathematical
findings were beginning to be appreciated from 1915
to 1919.
 His achievements were to be fully understood much
later, well after his untimely death in 1920.
 For example, his work on the highly composite
numbers started a whole new line of investigations in
the theory of such numbers.

EPONYMS
Magic Square
Brocard –
Ramanujan
Diophatine
equation
Dougall –
Ramanujan
identity
Hardy –
Ramanujan
number
Landau –
Ramanujan
constant
Ramanujan’s
congruences
Ramanujan –
Nagell equation
Ramanujan –
Peterssen
conjecture
Ramanujan –
Skolem’s
theorem
Ramanujan –
Soldner constant
Ramanujan
summation
Ramanujan theta
function
Ramanujan
graph
Ramanujan’s tau
function
Ramanujan’s
ternary quadratic
form
Ramanujan’s
prime
Ramanujan’s
costant
Ramanujan’s
sum
Rogers –
Ramanujan’s
identity
12/22/2014
VEERARAGAVAN C S
veeraa1729@gmail.com
Confidential 49

LESSONS LEARNT &/
UNLEARNT
 Despite the hardship faced by Ramanujan, he
rose to such a scientific standing and
reputation.
 No Indians has enjoyed before, should be
enough for young Indians to comprehend that
 If they are deserving and can work hard, they
can perhaps soar the way what Ramanujan
had.

 Even today in India, Ramanujan cannot get a
lectureship in a school / college because he had
no degree.
 Many researchers / Universities will pursue
studies / researches on his work but he will
have to struggle to get even a teaching job.
LESSONS LEARNT &/
UNLEARNT

Even after more than 90 years of the death of
Ramanujan, the situation is not very different
as far the rigidity of the education system is
concerned.
Today also a ‘Ramanujan’ has to clear all
traditional subjects’ exams to get a degree
irrespective of being genius in one or more
different subjects.
LESSONS LEARNT &/
UNLEARNT

 He was offered a chair in India only after becoming a
Fellow of the Royal Society.
 But it is disgraceful that India’s talent has to wait for
foreign recognition to get acceptance in India or else
immigrate to other places.
 Many of those won international recognition including
noble prizes had no other option but to migrate for
opportunities & recognition.(Ex. Karmerkar)
 The process of this brain drain is still continuing.
LESSONS LEARNT &/
UNLEARNT

 The most important lesson that we should
draw from Ramanujan’s life about the
condition of
 The Educational systems / provisions should
be made to support specially gifted children
with very strong interests in one direction, at
all stages of the educational system. (like
SUPER 30, INSPIRE AWARD ETC.,
LESSONS LEARNT &/
UNLEARNT

SRINIVASA RAMANUJAN
AND HIS MAGIC
SQUARE
12/22/2014
VEERARAGAVAN C S
Confidential 55

RAMANUJAN’S MAGIC SQUARE
22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
This square looks like
any other normal magic
square. But this is
formed by great
mathematician of our
country – Srinivasa
Ramanujan.
What is so great in it?
12/22/2014
VEERARAGAVAN C S
Confidential 56

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Sum of numbers of
any row is 139.
What is so great in it.?
12/22/2014
VEERARAGAVAN C S
Confidential 57

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Sum of numbers of
any column is also 139.
Oh, this will be there in
any magic square.
What is so great in it..?
12/22/2014
VEERARAGAVAN C S
Confidential 58

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Sum of numbers of
any diagonal is also
139.
Oh, this also will be there
in any magic square.
What is so great in it…?
12/22/2014
VEERARAGAVAN C S
Confidential 59

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Sum of corner
numbers is also 139.
Interesting?
12/22/2014
VEERARAGAVAN C S
Confidential 60

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Look at these
possibilities. Sum of
identical coloured
boxes is also 139.
Interesting..?
12/22/2014
VEERARAGAVAN C S
Confidential 61

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Look at these
possibilities. Sum of
identical coloured
boxes is also 139.
Interesting..?
12/22/2014
VEERARAGAVAN C S
Confidential 62

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Look at these central
squares.
Interesting…?
12/22/2014
VEERARAGAVAN C S
Confidential 63

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Can you try these
combinations?
Interesting…..?
12/22/2014
VEERARAGAVAN C S
Confidential 64

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
Try these
combinations also?
Interesting.…..?
12/22/2014
VEERARAGAVAN C S
Confidential 65

22 12 18 87
88 17 9 25
10 24 89 16
19 86 23 11
It is 22nd Dec 1887.
Yes. It is 22.12.1887
BE A PROUD INDIAN
12/22/2014
VEERARAGAVAN C S
Confidential 66

“When food is the problem,
how can I find money for
paper? I may require four
reams of paper every
month.”
Deplorable Condition of
Ramanujan

CONTRIBUTION TO THE
THEOREY OF PARTITIONS
N No. of
PARTITIONS
1 1
2 2
3 3
4 5
5 7
6 11
A partition of a
natural number
‘n’ is a
sequence of
non-decreasing
positive
integers whose
sum is ‘n’.
12/22/2014
VEERARAGAVAN C S
Confidential 72

Example:
For N=4,PARTITIONS are
4 = 4
=1+3
=2+2
=1+1+2
=1+1+1+1
P(4)=5,Whether P is a partition function
The highest highly composite
number listed by Ramanujan is
6746328388800
Having 10080 factors

The last three Books of Ramanujan
12/22/2014
VEERARAGAVAN C S
Confidential 74

Calculations of Ramanujan in his
own handwriting
12/22/2014
VEERARAGAVAN C S
Confidential 75

12/22/2014
VEERARAGAVAN C S
Confidential 76

12/22/2014
VEERARAGAVAN C S
Confidential 77

12/22/2014
VEERARAGAVAN C S
Confidential 78

Mock Theta Functions
12/22/2014
VEERARAGAVAN C S
Confidential 79

TOUGH LIFE IN ENGLAND
Pure vegetarian meals was not
available.
Too busy with calculations and
very often neglected food and
spent till late night.
The cold and damp climate
disturbed his health.
He was attacked by
Tuberculosis.
He returned to India.

Ramanujan sailed to Indian
on 27 february 1919 and
arrived on 13 march
However his health was very
poor.
He passed away on 26th April
1920 at Kumbakonam(Tamil
naidu)
We Miss a Great
Mathematician

Recognition by Govt.of
India
The Prime Minister of India,
Dr. Manmohan Singh has
declared the year 2012 as the
“National Mathematical Year”
and the date December 22,
being the birthday of Srinivasa
Ramanujan has been declared
as the
National Mathematics day” to
be celebrated every year

12/22/2014
VEERARAGAVAN C S
Confidential 85

Srinivasaramanujan a reminiscence 3

More Related Content

What's hot

Viewers also liked

Similar to Srinivasaramanujan a reminiscence 3

More from Veeraragavan Subramaniam

Recently uploaded

Srinivasaramanujan a reminiscence 3