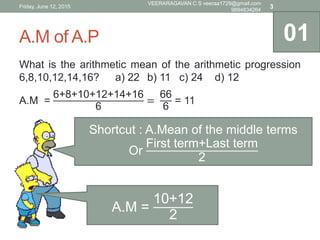
The document contains a series of arithmetic progression (A.P) and geometric progression (G.P) problems along with their solutions and explanations. Concepts such as the nth term, arithmetic mean, geometric mean, and sums of terms in both A.P and G.P are discussed. It includes multiple choice questions with calculations dated June 12, 2015.