Srinivasa Ramanujan was an Indian mathematician born in 1887 in India. He was largely self-taught and made extraordinary contributions to mathematical analysis, number theory, infinite series, and continued fractions. Despite having no formal training, he rediscovered theorems and produced new original work. He collaborated with G.H. Hardy at Cambridge University in England, where he became a Fellow. Ramanujan died young at the age of 32 in 1920. He independently compiled nearly 3900 mathematical results, most of which have been proven correct. He introduced unconventional concepts that have inspired further research.

3. December 22, 1887,
Erode
April 26, 1920,
Chetput,Chennai
Trinity College,
Cambridge
(1919–1920)
Kumbakonam,
Tamil Nadu

4. PARENTS :
SPOUSE :
ACADEMIC
ADVISOR:
Komalatammal,
K. Srinivasa Iyengar
Janakiammal
G. H. Hardy
J. E. Littlewood
Signature

6. Srinivasa Ramanujan ( 22 December 1887 – 26 April 1920) was an Indian
mathematician autodidact who, with almost no formal training in pure
mathematics, made extraordinary contributions to mathematical analysis,
number theory, infinite series, and continued fractions. Living in India with no
access to the larger mathematical community, which was centred in Europe at
the time, Ramanujan developed his own mathematical research in isolation. As
a result, he rediscovered known theorems in addition to producing new work.
Ramanujan was said to be a natural genius by the English mathematician G. H.
Hardy, in the same league as mathematicians such as Euler and Gauss. He
died at the age of 32.
Ramanujan was born at Erode, Madras Presidency (now Tamil Nadu) in
a Tamil Brahmin family of Thenkalai Iyengar sect. His introduction to
formal mathematics began at age 10. He demonstrated a natural ability, and
was given books on advanced trigonometry written by S. L. Lone that he
mastered by the age of 12 ; he even discovered theorems of his own, and re-
discovered Euler's identity independently. He demonstrated unusual
mathematical skills at school, winning accolades and awards. By 17,
Ramanujan had conducted his own mathematical research on Bernoulli
numbers and the Euler–Mscheroni constant.

7. Ramanujan received a scholarship to study at Government College in Kumbakonam,
which was later rescinded when he failed his non-mathematical coursework. He joined
another college to pursue independent mathematical research, working as a clerk in the
Accountant-General's office at the Madras Port Trust Office to support himself. In 1912–
1913, he sent samples of his theorems to three academics at the University of
Cambridge. G. H. Hardy, recognizing the brilliance of his work, invited Ramanujan to
visit and work with him at Cambridge. He became a Fellow of the Royal Society and a
Fellow of Trinity College, Cambridge. Ramanujan died of illness, malnutrition, and
possibly liver infection in 1920 at the age of 32.
During his short lifetime, Ramanujan independently compiled nearly 3900 results
(mostly identities and equations). Nearly all his claims have now been proven correct,
although a small number of these results were actually false and some were already
known. He stated results that were both original and highly unconventional, such as
the Ramanujan prime and the Ramanujan theta function, and these have inspired a vast
amount of further research. However, the mathematical mainstream has been rather
slow in absorbing some of his major discoveries. The Ramanujan Journal, an
international publication, was launched to publish work in all areas of mathematics
influenced by his work.
In December 2011, in recognition of his contribution to mathematics, the
Government of India declared that Ramanujan's birthday (22 December) should
be celebrated every year as National Mathematics Day, and also declared 2012
the National Mathematics Year.

8. The number 1729 is known as the Hardy–Ramanujan number after a
famous anecdote of the British mathematician G. H. Hardy regarding a
visit to the hospital to see Ramanujan. In Hardy's words:
I remember once going to see him when he was ill at Putney. I had
ridden in taxi cab number 1729 and remarked that the number
seemed to me rather a dull one, and that I hoped it was not an
unfavorable omen. "No," he replied, "it is a very interesting
number; it is the smallest number expressible as the sum of two
cubes in two different ways."
“
”

9. The two different ways are :-
1729 = 13 + 123
{OR}
1729 = 93 + 103.
Generalizations of this idea have created the
notion of "taxicab numbers". Coincidentally, 1729
is also a Carmichael number .

10. In mathematics, there is a distinction between having an insight and having a proof. Ramanujan's
talent suggested a plethora of formulae that could then be investigated in depth later. It is said that
Ramanujan's discoveries are unusually rich and that there is often more to them than initially meets
the eye. As a by-product, new directions of research were opened up. Examples of the most
interesting of these formulae include the intriguing infinite series for π, one of which is given below
This result is based on the negative fundamental discriminant d = −4×58 = −232 with class
number h(d) = 2 (note that 5×7×13×58 = 26390 and that 9801=99×99; 396=4×99) and is related to
the fact that
Compare to Heegner numbers, which have class number 1 and yield similar formulae. Ramanujan's
series for π converges extraordinarily rapidly (exponentially) and forms the basis of some of the
fastest algorithms currently used to calculate π. Truncating the sum to the first term also gives the
approximation
for π, which is correct to six decimal places.

11. One of his remarkable capabilities was the rapid solution for problems. He was sharing a room
with P. C. Mahalanobis who had a problem, "Imagine that you are on a street with houses marked 1
through n. There is a house in between (x) such that the sum of the house numbers to left of it
equals the sum of the house numbers to its right. If n is between 50 and 500, what are n and x?"
This is a bivariate problem with multiple solutions. Ramanujan thought about it and gave the answer
with a twist: He gave a continued fraction. The unusual part was that it was the solution to the
whole class of problems. Mahalanobis was astounded and asked how he did it. "It is simple. The
minute I heard the problem, I knew that the answer was a continued fraction. Which continued
fraction, I asked myself. Then the answer came to my mind," Ramanujan replied.
His intuition also led him to derive some previously unknown identities, such as
for all ,where is the gamma function. Expanding into series of
powers and equating coefficients of
gives some deep identities for the hyperbolic secant.

12. In 1918, Hardy and Ramanujan studied the partition
function P(n) extensively and gave a non-convergent
asymptotic series that permits exact computation of the
number of partitions of an integer.Hans Rademacher, in
1937, was able to refine their formula to find an exact
convergent series solution to this problem. Ramanujan
and Hardy's work in this area gave rise to a powerful
new method for finding asymptotic formulae, called
the circle method.
He discovered mock theta functions in the last year of
his life. For many years these functions were a mystery,
but they are now known to be the holomorphic parts of
harmonic weak Maass forms.

15. Explanation of Lunar eclipse and Solar
eclipse, Rotation of earth on its axis,
Reflection of light by moon, Sinusoidal
functions, Solution of single variable
quadratic equation, Value of π correct to
4 decimal places, Circumference of Earth
to 99.8% accuracy, Calculation of the
length of Sidereal year.

16. Name
While there is a tendency to misspell his name as "Aryabhatta" by
analogy with other names having the "bhatta" suffix, his name is
properly spelled Aryabhata: every astronomical text spells his
name thus, including Brahmagupta's references to him "in more
than a hundred places by name". Furthermore, in most instances
"Aryabhatta" does not fit the metre either.
Time and place of birth
Aryabhata mentions in the Aryabhatiya that it was composed
3,600 years into the Kali Yuga, when he was 23 years old. This
corresponds to 499 CE, and implies that he was born in 476.
Aryabhata's birthplace is uncertain, but it may have been in the
area known in ancient texts as Ashmaka India which may have
been Maharashtra or Dhaka.

17. Education
It is fairly certain that, at some point, he went to Kusumapura for advanced studies
and lived there for some time. Both Hindu and Buddhist tradition, as well as Bhāskara
I (CE 629), identify Kusumapura as Pāṭaliputra, modern Patna. A verse mentions that
Aryabhata was the head of an institution (kulapa) at Kusumapura, and, because the
university of Nalanda was in Pataliputra at the time and had an astronomical
observatory, it is speculated that Aryabhata might have been the head of the Nalanda
university as well. Aryabhata is also reputed to have set up an observatory at the Sun
temple in Taregana, Bihar.
Other hypotheses
Some archeological evidence suggests that Aryabhata could have originated from the
present day Kodungallur which was the historical capital city of Thiruvanchikkulam of
ancient Kerala. For instance, one hypothesis was that aśmaka (Sanskrit for "stone")
may be the region in Kerala that is now known as Koṭuṅṅallūr, based on the belief
that it was earlier known as Koṭum-Kal-l-ūr ("city of hard stones"); however, old
records show that the city was actually Koṭum-kol-ūr ("city of strict governance").
Similarly, the fact that several commentaries on the Aryabhatiya have come from
Kerala were used to suggest that it was Aryabhata's main place of life and activity;
however, many commentaries have come from outside Kerala.
Aryabhata mentions "Lanka" on several occasions in the Aryabhatiya, but his "Lanka"
is an abstraction, standing for a point on the equator at the same longitude as his
Ujjayini.

18. Works
Aryabhata is the author of several treatises on mathematics and astronomy, some of
which are lost.
His major work, Aryabhatiya, a compendium of mathematics and astronomy, was
extensively referred to in the Indian mathematical literature and has survived to modern
times. The mathematical part of the Aryabhatiya covers arithmetic, algebra, plane
trigonometry, and spherical trigonometry. It also contains continued fractions, quadratic
equations, sums-of-power series, and a table of sines.
The Arya-siddhanta, a lot work on astronomical computations, is known through the
writings of Aryabhata's contemporary, Varahamihira, and later mathematicians and
commentators, including Brahmagupta and Bhaskara I. This work appears to be based on
the older Surya Siddhanta and uses the midnight-day reckoning, as opposed to sunrise in
Aryabhatiya. It also contained a description of several astronomical instruments: the
gnomon (shanku-yantra), a shadow instrument (chhAyA-yantra), possibly angle-
measuring devices, semicircular and circular (dhanur-yantra / chakra-yantra), a cylindrical
stick yasti-yantra, an umbrella-shaped device called the chhatra-yantra, and water clocks
of at least two types, bow-shaped and cylindrical.
A third text, which may have survived in the Arabic translation, is Al ntf or Al-nanf. It claims
that it is a translation by Aryabhata, but the Sanskrit name of this work is not known.
Probably dating from the 9th century, it is mentioned by the Persian scholar and chronicler
of India, Abū Rayhān al-Bīrūnī.

19. Place value system and zero
The place-value system, first seen in the 3rd-century Bakhshali Manuscript, was
clearly in place in his work. While he did not use a symbol for zero, the French
mathematician Georges Ifrah argues that knowledge of zero was implicit in
Aryabhata's place-value system as a place holder for the powers of ten with null
coefficients
However, Aryabhata did not use the Brahmi numerals. Continuing
the Sanskrit tradition from Vedic times, he used letters of the alphabet to denote
numbers, expressing quantities, such as the table of sines in a mnemonic form.
Algebra
In Aryabhatiya Aryabhata provided elegant results for the summation
of series of squares :-

20. Trigonometry
In Ganitapada 6, Aryabhata gives the area of a triangle as
tribhujasya phalashariram samadalakoti bhujardhasamvargah
that translates to: "for a triangle, the result of a perpendicular with the half-side is the
area."
Aryabhata discussed the concept of sine in his work by the name of ardha-jya, which
literally means "half-chord". For simplicity, people started calling it jya. When Arabic
writers translated his works from Sanskrit into Arabic, they referred it as jiba. However, in
Arabic writings, vowels are omitted, and it was abbreviated as jb. Later writers
substituted it with jaib, meaning "pocket" or "fold (in a garment)". (In Arabic, jiba is a
meaningless word.) Later in the 12th century, when Gherardo of Cremona translated
these writings from Arabic into Latin, he replaced the Arabic jaib with its Latin
counterpart, sinus, which means "cove" or "bay"; thence comes the English sine.
Alphabetic code has been used by him to define a set of increments. If we use
Aryabhata's table and calculate the value of sin(30) (corresponding to hasjha) which is
1719/3438 = 0.5; the value is correct. His alphabetic code is commonly known as the
Aryabhata cipher.

21. Statue of Aryabhata on the
grounds of IUCAA, Pune.
As there is no known
information regarding his
appearance, any image of
Aryabhata originates from
an artist's conception.

23. Born November 4, 1929
Bangalore, India
Died April 21, 2013 (aged 83)
Bangalore, Karnataka, India
Cause of death Respiratory and cardiac problems
Nationality Indian
Other names Human computer

24. Shakuntala Devi was born in Bangalore, India, to an
orthodox Kannada Brahmin family. Her father rebelled
against becoming a temple priest and instead joined a
circus where he worked as a trapeze artist, lion
tamer, tightrope walker and magician. Devi's father
discovered her ability to memorize numbers while teaching
her a card trick when she was about three years old. Her
father left the circus and took her on road shows that
displayed her ability at number crunching. She was able to
do this without any formal education. By age six she
demonstrated her calculation and memorization abilities at
the University of Mysore.
In 1944 Devi moved to London with her father. She
returned to India in the mid-1960s and married Paritosh
Bannerji, an officer of the Indian Administrative Service
from Kolkata. She and her husband were divorced in
1979. Devi returned to Bangalore in the early 1980s.

25. Devi travelled the world demonstrating her arithmetic talents,
including a tour of Europe in 1950 and a performance in New York
in 1976. In 1988 she returned to the US to have her abilities
studied by Arthur Jensen, a professor of psychology at
the University of California, Berkeley. Jensen tested her
performance at several tasks, including the calculations of large
numbers; Examples of the problems presented to Devi were
calculating the cube root of 61,629,875, and the seventh root of
170,859,375. Jensen reported that Devi was able to provide the
solution to the aforementioned problems (the answers being 395
and 15 respectively) before Jensen was able to copy them down
in his notebook. Jensen published his findings in the academic
journal Intelligence in 1990.
In addition to her work as a mental calculator, Devi was
an astrologer and an author of several books, including
cookbooks and fictional novels.

26. •In 1977 in USA she competed with a computer to see who
gives the cube root of 188138517 faster, she won. That same
year, at the Southern Methodist University she was asked to
give the 23rd root of a 201-digit number; she answered in 50
seconds. Her answer—546,372,891—was confirmed by
calculations done at the U.S. Bureau of Standards by the
Univac 1101 computer, for which a special program had to be
written to perform such a large calculation.
•On June 18, 1980, she demonstrated the multiplication of
two 13-digit numbers 7,686,369,774,870 ×
2,465,099,745,779 picked at random by the Computer
Department of Imperial College, London. She correctly
answered 18,947,668,177,995,426,462,773,730 in 28
seconds. This event is mentioned in the 1982 Guinness Book
of Records.

27. Death
In April of 2013, Devi was admitted to a hospital in Bangalore,
India with respiratory problems. Over the following 2 weeks she
suffered from complications of the heart and kidneys. Devi died in
hospital on April 21, 2013. She was 83 years old. Devi is survived
by her daughter, Anupama Banerji.
Shakuntala Devi,
May 19, 2006

29. Pingala
Born
4th century BC
Shalatula
Died (unknown)
Era Vedic period
Region Indian subcontinent
Main interests
Indian mathematics, Sanskrit
grammar
Notable ideas
mātrāmeru, binary numeral
system, arithmetical triangle
Major works
Author of the Chandaḥśāstra (also
Chandaḥsūtra), the earliest
known Sanskrit treatise
on prosody

30. Pingala (is the traditional name of the author of
the Chandaḥśāstra (also Chandaḥsūtra), the earliest known Sanskrit
treatise on prosody.
Little is known about Piṅgala himself. In Indian literary tradition, he
is variously identified either as the younger brother of Pāṇini (4th
century BCE), or as Patañjali, the author of
the Mahabhashya (2nd century BCE).
The Chandaḥśāstra is a work of eight chapters in the
late Sūtra style, not fully comprehensible without a commentary. It
has been dated to either the final centuries BCE or the early
centuries CE, at the transition between Vedic meter and
the classical meter of the Sanskrit epics. This would place it close
to the beginning of the Common Era, likely post-
dating Mauryan times. The 10th century
mathematician Halayudha wrote a commentary on
the Chandaḥśāstra and expanded it.

31. Combinatorics
The Chandaḥśāstra presents the first known
description of a binary numeral system in
connection with the systematic enumeration of
meters with fixed patterns of short and long
syllables. The discussion of the combinatorics of
meter corresponds to the binomial theorem.
Halāyudha's commentary includes a presentation
of the Pascal's triangle (called meruprastāra).
Pingala's work also contains the Fibonacci
number, called mātrāmeru, and now known as
the Gopala–Hemachandra number.

32. Use of zero is sometimes mistakenly ascribed to Pingala
due to his discussion of binary numbers, usually
represented using 0 and 1 in modern discussion, while
Pingala used short and long syllables. As Pingala's
system ranks binary patterns starting at one (four short
syllables—binary "0000"—is the first pattern), the nth
pattern corresponds to the binary representation of n-1,
written backwards. Positional use of zero dates from
later centuries and would have been known to
Halāyudha but not to Pingala.

34. Born 505 CE
Died 587 CE
Occupation
Astronomer, mathematician,
and astrologer
Nationality Indian
Ethnicity Indian
Period Gupta era
Subjects
Astronomy, Astrology,
Mathematics
Notable work(s)
Pancha-Siddhāntikā, Brihat-

35. Varāhamihira
Varahamihra (Devanagari: वराहमिहहर) (505–587 CE),
also called Varaha or Mihir, was an Indian astronomer,
mathematician, and astrologer who lived in Ujjain. He
was born in Avanti region, roughly corresponding to
modern day Malwa, to Adityadasa, who was himself an
astronomer. According to one of his own works, he was
educated at Kapitthaka. He is considered to be one of
the nine jewels (Navaratnas) of the court of legendary
ruler Yashodharman Vikramaditya of Malwa.

36. Pancha-Siddhantika
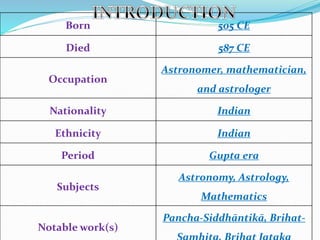
Varahamihir's main work is the book Pañcasiddhāntikā (or Pancha-Siddhantika,
"[Treatise] on the Five [Astronomical] Canons) dated ca. 575 CE gives us information
about older Indian texts which are now lost. The work is a treatise on mathematical
astronomy and it summaries five earlier astronomical treatises, namely the Surya
Siddhanta, Romaka Siddhanta, Paulisa Siddhanta, Vasishtha Siddhanta and
Paitamaha Siddhantas. It is a compendium of Vedanga Jyotisha as well as Hellenistic
astronomy (including Greek, Egyptian and Roman elements). He was the first one to
mention in his work Pancha Siddhantika that the ayanamsa, or the shifting of the
equinox is 50.32 seconds.
The 11th century Iranian scholar Alberuni also described the details of "The Five
Astronomical Canons":
"They [the Indians] have 5 Siddhāntas:
Sūrya-Siddhānta, i.e.. the Siddhānta of the Sun, composed by Lāṭadeva,
Vasishtha-siddhānta , so called from one of the stars of the Great Bear,
composed by Vishnucandra,
Pulisa-siddhānta, so called from Paulisa, the Greek, from the city of Saintra,
which is supposed to be Alexandria, composed by Pulisa.
Romaka-siddhānta, so called from the Rūm, i.e.. the subjects of the Roman
Empire, composed by Śrīsheṇa.

37. Brihat-Samhita
Another important contribution of Varahamihira is
the encyclopedic Brihat-Samhita. It covers wide
ranging subjects of human interest, including
astrology, planetary movements, eclipses, rainfall,
clouds, architecture, growth of crops,
manufacture of perfume, matrimony, domestic
relations, gems, pearls, and rituals. The volume
expounds on gemstone evaluation criterion found
in the Garuda Purana, and elaborates on the
sacred Nine Pearls from the same text. It
contains 106 chapters and is known as the "great
compilation".

38. Trigonometry
Varahamihira's mathematical work included the
discovery of the trigonometric formulas
Varahamihira improved the accuracy of the sine
tables of Aryabhata I.

39. Arithmetic
He defined the algebraic properties of zero as well as of negative numbers.
Combinatorics
He was among the first mathematicians to discover a version of what is now
known as the Pascal's triangle. He used it to calculate the binomial coefficients.
Optics
Among Varahamihira's contribution to physics is his statement that reflection is
caused by the back-scattering of particles and refraction (the change of direction
of a light ray as it moves from one medium into another) by the ability of the
particles to penetrate inner spaces of the material, much like fluids that move
through porous objects.
1. ^ "the Pañca-siddhāntikā ("Five Treatises"), a compendium of Greek, Egyptian,
Roman and Indian astronomy. Varāhamihir's knowledge of Western astronomy
was thorough. In 5 sections, his monumental work progresses through native
Indian astronomy and culminates in 2 treatises on Western astronomy, showing
calculations based on Greek and Alexandrian reckoning and even giving
complete Ptolemaic mathematical charts and tables. Encyclopedia Britannica
(2007) s.v.Varahamihira ^
2. E. C. Sachau, Alberuni's India (1910), vol. I, p. 153

41. Brahmagupta (597–668 AD) was an Indian
mathematician and astronomer who wrote two important
works on mathematics and astronomy: the
Brāhmasphuṭasiddhānta (Extensive Treatise of Brahma)
(628), a theoretical treatise, and the Khaṇḍakhādyaka, a
more practical text. There are reasons to believe that
Brahmagupta originated from Bhinmal.
Brahmagupta was the first to give rules to compute with
zero. The texts composed by Brahmagupta were
composed in elliptic verse, as was common practice in
Indian mathematics, and consequently has a poetic ring
to it. As no proofs are given, it is not known how
Brahmagupta's mathematics was derived.

42. Series
Brahmagupta then goes on to give the sum of the squares and cubes of the
first n integers.
12.20. The sum of the squares is that [sum] multiplied by twice the [number
of] step[s] increased by one [and] divided by three. The sum of the cubes is
the square of that [sum] Piles of these with identical balls [can also be
computed].
Here Brahmagupta found the result in terms of the sum of the first n integers,
rather than in terms of n as is the modern practice.
He gives the sum of the squares of the first n natural numbers as
n(n+1)(2n+1)/6 and the sum of the cubes of the first n natural numbers as
(n(n+1)/2)².
ALGEBRA
=
and

43. Brahmagupta's most famous result in geometry is
his formula for cyclic quadrilaterals. Given the lengths
of the sides of any cyclic quadrilateral, Brahmagupta
gave an approximate and an exact formula for the
figure's area,
The approximate area is the product of the halves of
the sums of the sides and opposite sides of a triangle
and a quadrilateral. The accurate [area] is the square
root from the product of the halves of the sums of the
sides diminished by [each] side of the quadrilateral.
So given the lengths p, q, r and s of a cyclic
quadrilateral, the approximate area is
while, letting
the exact area is
Although Brahmagupta does not explicitly state that these quadrilaterals are cyclic, it is
apparent from his rules that this is the case. Heron's formula is a special case of this
formula and it can be derived by setting one of the sides equal to zero.

45. Works
He was known for two treatises: Trisatika
(sometimes called the Patiganitasara) and
the Patiganita. His major work Patiganitasara
was named Trisatika because it was written
in three hundred slokas. The book discusses
counting of numbers, measures, natural
number, multiplication, division, zero,
squares, cubes, fraction, rule of three,
interest-calculation, joint business or
partnership and mensuration.

46. He gave an exposition on zero. He has written, "If 0(zero) is
added to any number,the sum is the same number; If 0(zero) is
subtracted from any number,the number remains unchanged; If
0(zero) is multiplied by any number, the product is 0(zero)". He
has said nothing about division of any number by 0(zero).
In the case of dividing a fraction he has found out the method of
multiplying the fraction by the reciprocal of the divisor.
He wrote on practical applications of algebra separated algebra
from arithmetic
He was one of the first to give a formula for solving quadratic
equations.
He found the formula :-
(Multiply by 4a)

47. Biography
Sridhara is now believed to have lived in the ninth and tenth
centuries. However, there has been much dispute over his date and
in different works the dates of the life of Sridhara have been placed
from the seventh century to the eleventh century. The best present
estimate is that he wrote around 900 AD, a date which is deduced
from seeing which other pieces of mathematics he was familiar with
and also seeing which later mathematicians were familiar with his
work. Some historians give Bengal as the place of his birth while
other historians believe that Sridhara was born in southern India.
Sridhara is known as the author of two mathematical treatises,
namely the Trisatika (sometimes called the Patiganitasara ) and the
Patiganita. However at least three other works have been attributed
to him, namely the Bijaganita, Navasati, and Brhatpati. Information
about these books was given the works of Bhaskara II (writing
around 1150), Makkibhatta (writing in 1377), and Raghavabhatta
(writing in 1493).

48. K.S. Shukla examined Sridhara's method for finding rational
solutions of
, ,,
which Sridhara gives in the Patiganita. Shukla states that the
rules given there are different from those given by other Hindu
mathematicians.
Sridhara was one of the first mathematicians to give a rule to
solve a quadratic equation. Unfortunately, as indicated above,
the original is lost and we have to rely on a quotation of
Sridhara's rule from Bhaskara II:-
Multiply both sides of the equation by a known quantity equal to
four times the coefficient of the square of the unknown; add to
both sides a known quantity equal to the square of the
coefficient of the unknown; then take the square root.