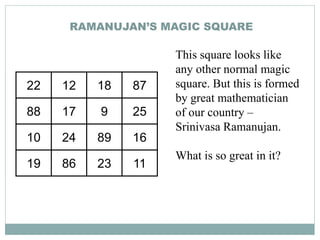
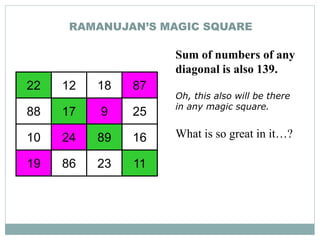
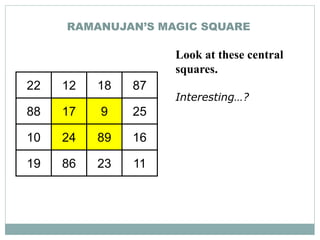
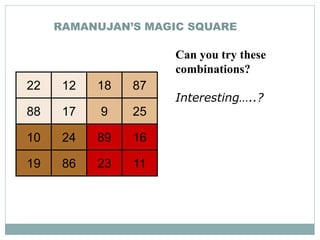
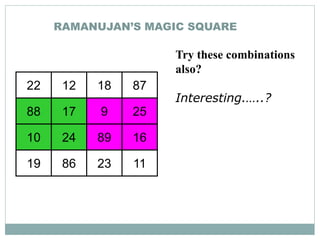
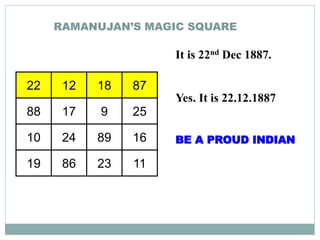
Srinivasa Ramanujan (1887-1920) was a renowned Indian mathematician. He showed early signs of genius in mathematics as a child. He was self-taught and made significant contributions to mathematical analysis, number theory, infinite series, and continued fractions. Ramanujan developed his own theorems and results without any formal training. He was recognized by mathematicians in England and his work was found to be of extraordinary significance. However, he struggled with poor health and poverty, and ultimately died young at the age of 32 in India. Ramanujan is celebrated annually in India on his birthday as a brilliant mathematician who made major contributions despite facing disadvantages.