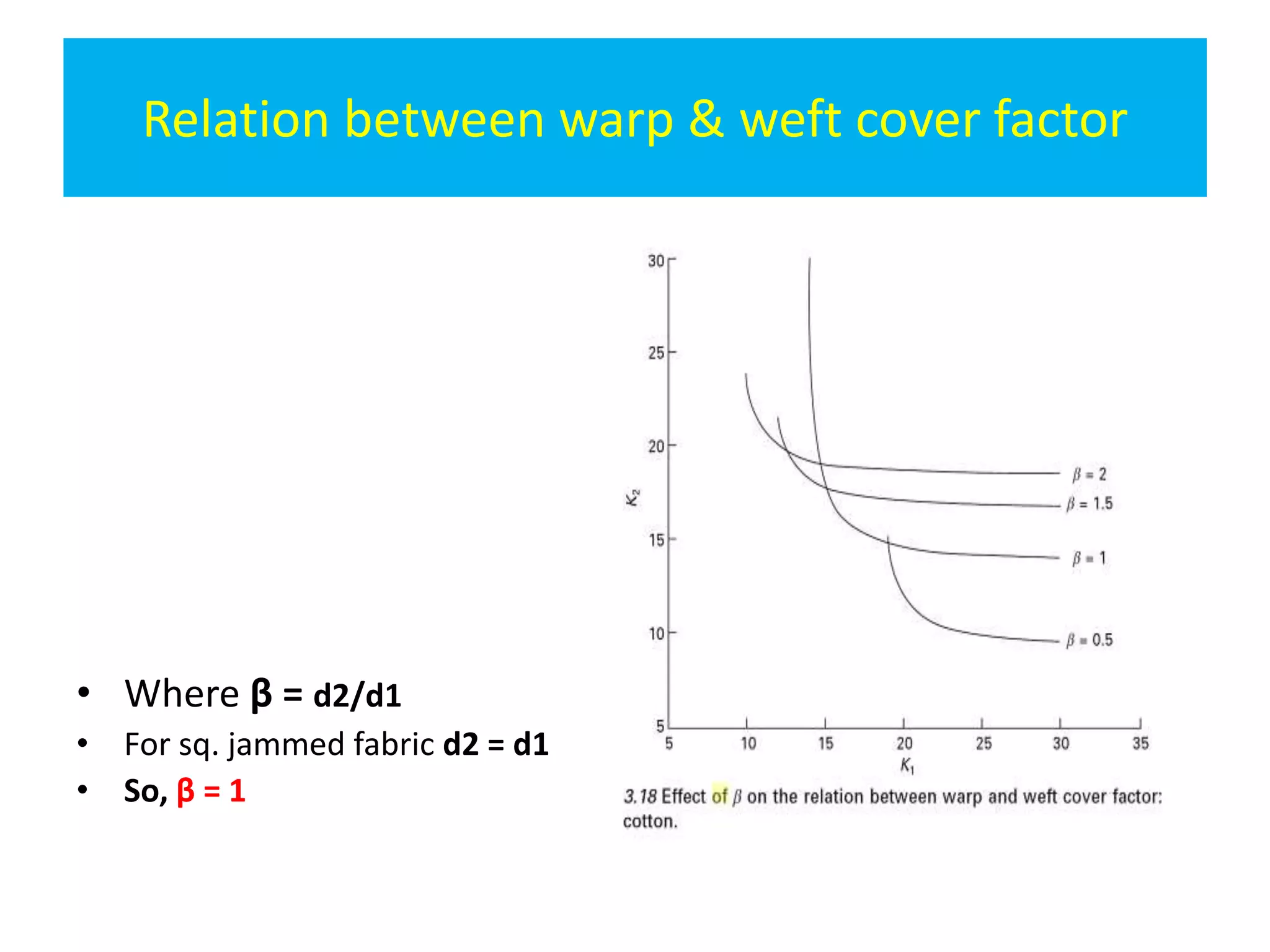
This document discusses jammed fabric structures and provides mathematical models to predict their properties. A jammed fabric is one where the warp and weft yarns are in intimate contact with no mobility between yarns. Pierce's model and the racetrack model are presented to calculate thread spacing, fabric cover, and crimp based on yarn diameters. A truly square jammed fabric has equal warp and weft spacing, crimp, and angles. Such a fabric has 20.9% crimp and cover factors of 16.2. Jammed fabrics are closely woven and used for waterproof, windproof and bulletproof applications.

1. WELCOME

2. SQUARE JAMMED
FABRIC
By
• SANJITJANA
• RAJABAHADURPAUL
• ANUPAMMULA
• MIRAJUL SK
• 3RD YEAR
• TEXTILE TECHNOLOGY

3. 1.Prediction of the maximum sett (density) of fabric and fabric
dimensions;
2.Find out relationship between geometrical parameters (picks
and ends);
3.Prediction of mechanical properties by combining fabric and
yarn properties;
4.Understanding fabric performance (handle and surface
effect.
INTRODUCTION
The objectives of fabric geometry is to:
Structure of a woven fabric is defined by weave pattern, thread
density, crimp and yarn count
3

4. Jammed structure
A woven fabric in which warp & weft yarns
don’t have mobility within the structure as
they are in intimate contact with each other
are called jammed structure. In such a
structure the warp & weft yarns will have
minimum thread spacing.

5. Pierce’s Model

6. Mathematical Notation for the model
• D1 & d2 - Warp & Weft diameter respectively
• D - Sum of circular diameter
• h1 & h2 -distance between axes of warp /weft & fabric
• p1 & p2 – Thread spacing of warp & weft respectively
• c1 & c2 - Crimp of warp & weft
• θ1 & θ2 – Max. angle of thread axis to plane of cloth
(radians)
• l1 & l2 - Moduler length of warp & weft respectively

7. Results of Pierce’s Model

8. Jamming Condition of a fabric
• During jamming the straight portion of the
intersecting yarn will vanish so that-
Jamming warp direction Jamming weft direction
l1–Dθ1 = 0 h2 = D(1 –cosθ2)
l1/D = 0 p1= Dsinθ2
So,
h1 = D(1 -cosθ1)
p2= Dsinθ1

9. Jamming both warp & weft direction
D = h1 + h2
D = D(1 -cosθ1) + D(1 –cosθ2)
Cosθ1 +cosθ2 = 1

10. Square Fabric
• A truly square fabric has equal diameter of
both warp & weft, equal spacing, equal crimp
p2= p1 , c1=c2 , h1=h2 , θ1= θ2
D=2d= h1+h2=2*4/3 p √c
√c =3/4 * d/p

11. Square Jammed fabric
For a sq. jammed fabric θ1 =θ2
So,
Cosθ1 +cosθ2 = 1
Cosθ = ½
θ = π/3
p=Dsinθ
&
l=Dθ

12. Racetrack Model
• In the racetrack model, a and b are maximum and minimum diameters of
the cross-section. The fabric parameters with superscript refer to the zone
AB, which is analogous to the circular thread geometry; the parameters
without superscript refer to the racetrack geometry, a repeat of this is
between C and D.
Then the basic equations will be modified as under:
p2’ = p2 – (a2 – b2)
l1’ = l1 – (a2 – b2)
h1 + h2 = B = b1 + b2
Also if both warp and weft threads are jammed,
the relationship becomes

13. Crimp of sq. jammed fabric
• The crimp in fabric is the most important parameter which influences
several fabric properties such as extensibility , thickness , compressibility
and handle. It also decides quantity of yarn required to weave a fabric
during manufacturing.
The crimp of a sq. jammed fabric is about 20.9 %
we know,
Crimp (c) =l/p -1 [p=Dsinθ &l= Dθ ]
= Dθ/Dsinθ -1
= θ/sinθ – 1
= π/3/sin π/3 - 1 [θ = π/3]
=1.209 -1
= .209
So, c % = 20.9 %

14. Cover factor of square jammed fabric
• In fabric, cover is considered as fraction of the total fabric
area covered by the component yarns.
The fractional cover factor (d/p) = 1/√3
1 X n = 1/√3
28 X √N
n/ √N = 16.2
So, cover factor of both warp & weft is 16.2 AC = 2d
k1 = k2 =16.2 AB = d
And Fabric cover factor is 23 So, BC = √3 d
k1 + k2- k1k2/28 = 23 p = √3 d

15. Relation between warp & weft cover factor
• Where β = d2/d1
• For sq. jammed fabric d2 = d1
• So, β = 1

16. Application of jammed fabric
Jammed fabric are closely woven fabric & find
application in water-proof , wind- proof, bullet-
proof requirements.

17. References
• Woven Textiles: Principles, Technologies and
Applications :- Edited by K Gandhi
• Woven Textile Structure: Theory and
Applications :- By B K Behera, P K Hari