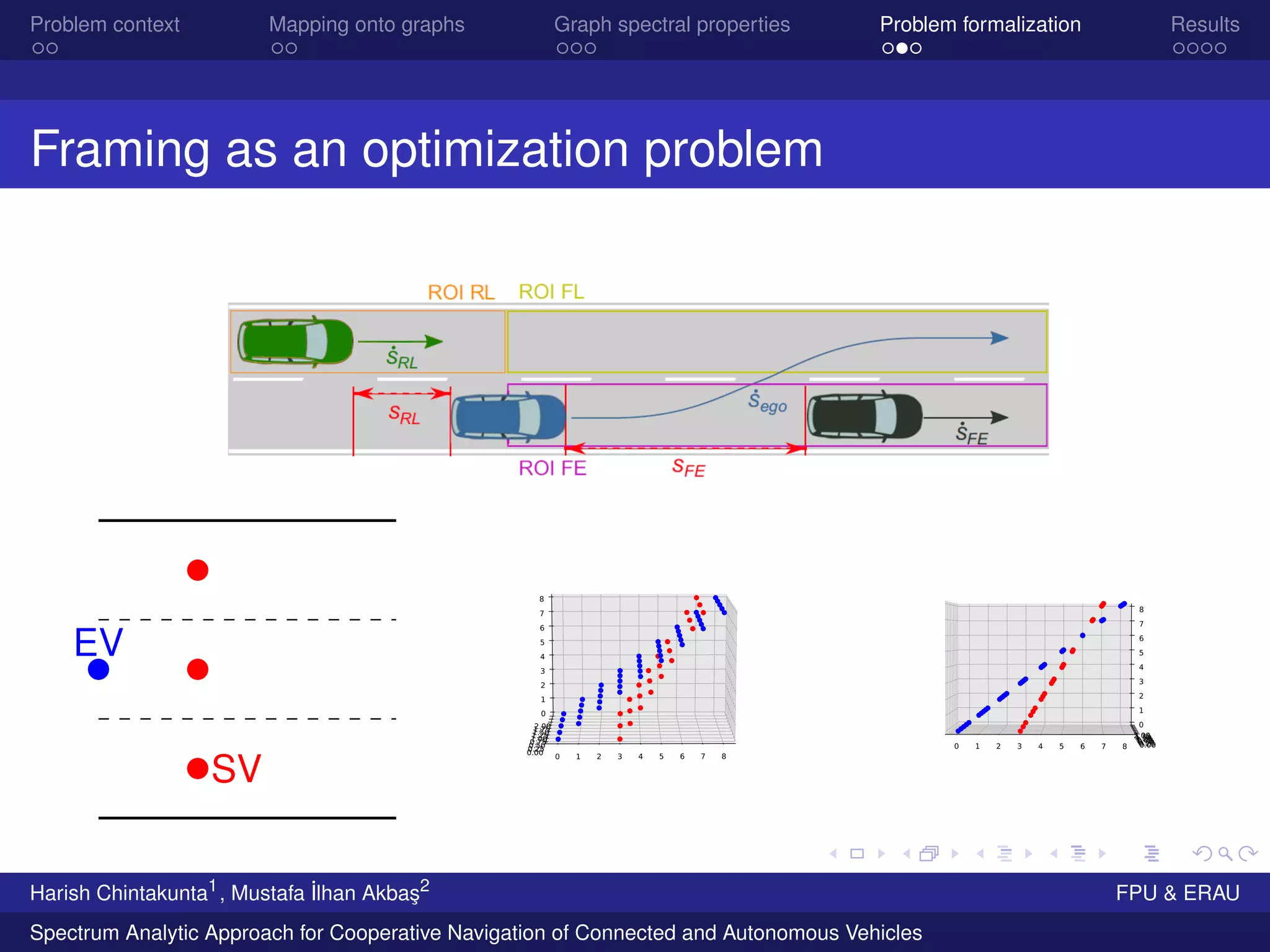
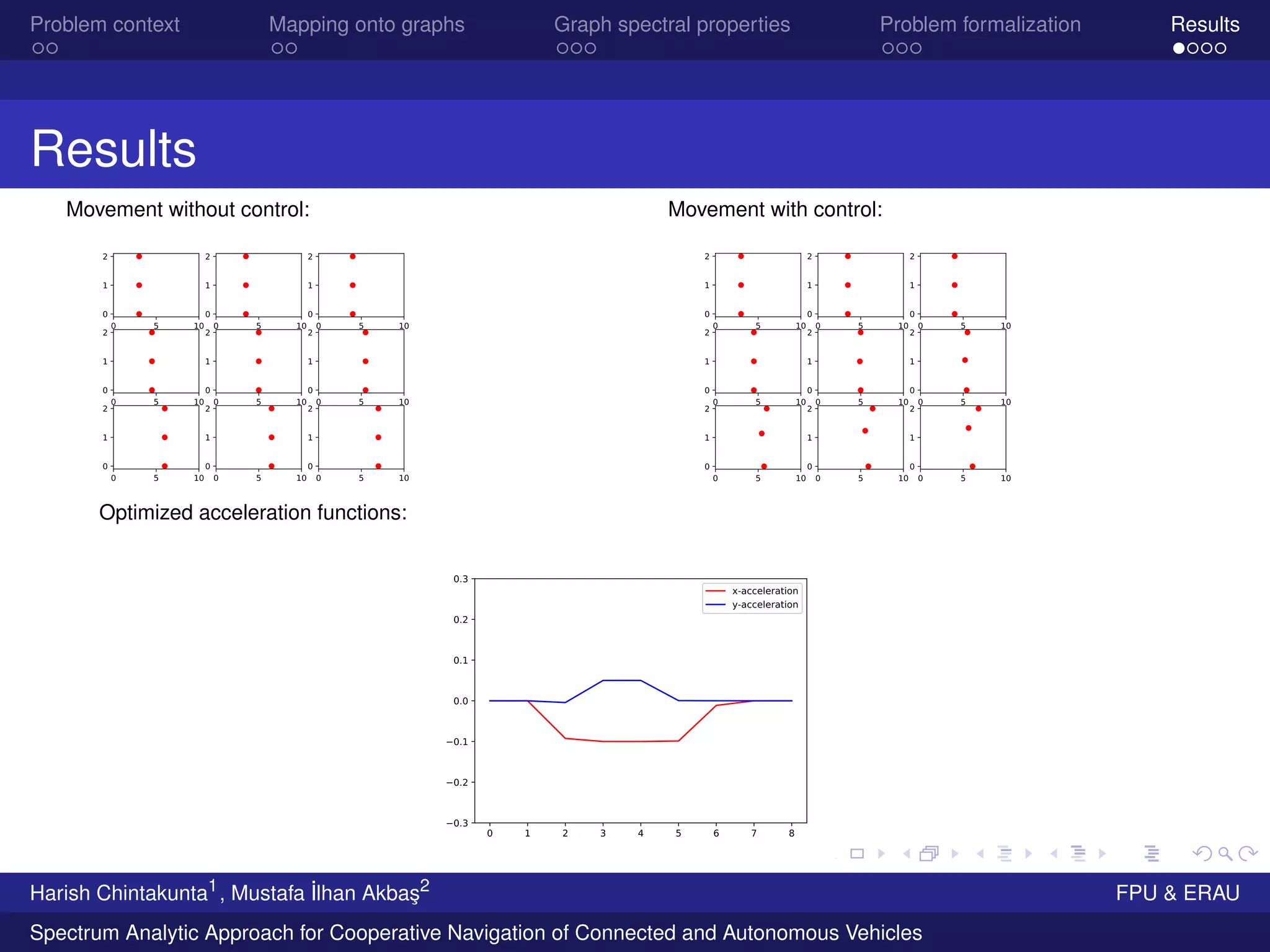
The document discusses a spectrum analytic approach for improving the cooperative navigation of connected and autonomous vehicles (CAVs) and emergency vehicles (EVs). It formulates the problem using graph theory to ensure safe navigation by optimizing the configuration and behaviors of surrounding vehicles. The results indicate that adjusting vehicle arrangements based on spectral properties can significantly enhance the safety and efficiency of emergency navigation.

1. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Spectrum Analytic Approach for Cooperative
Navigation of Connected and Autonomous
Vehicles
Harish Chintakunta1 Mustafa ˙Ilhan Akba¸s2
1Department of Electrical and Computer Engineering
Florida Polytechnic University
2Electrical, Computer, Software and Systems Engineering
Embry-Riddle Aeronautical University
9th ACM International Symposium on Design and Analysis of Intelligent Vehicular
Networks and Applications (DIVANET)
November 25, 2019
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

2. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Emergency vehicle navigation
Making way for the EV can take a
long time.
Drivers feel “hassled” at the
appearance of EVs, which leads
to bad decisions.
There are about 6,500 annual
accidents involving ambulances.
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

3. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Advantages of Connected Autonomous Vehicles (CAVs)
Vehicles can be notified well in advance about an
approaching EV.
Complex cooperative behavior amongst CAVs can assist
the navigation of EVs.
EV itself being autonomous can enable complex path
planning algorithm to optimize travel time, saving lives.
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

4. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Our view of the problem
We now consider the problem
when all other vehicles drive
cooperatively to assist an EV.
Facilitating safety for EV is
rephrased using topological
features.
The space of feasible paths
for EV should be “strongly
connected”, in other words,
no “bottle necks”.
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

5. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Formulation in terms of graph theory
1 Discretize the space and draw
edges between neighboring vertices.
2 Encode the safety information onto
edge weights.
3 The weight we = 1 − e−d(s,e)
on an
edge is a decreasing function of the
distance from a surrounding vehicle.
4 In this example, we would want the
surrounding vehicle to move away
from the central edge.
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

6. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Inspiration from spectral properties
Graph Laplacian L defined as
L = D − A,
has the following useful property (M.Fiedler, 1973):
λ2(L) ≤ σe(G),
where σe(G) is the edge connectivity.
More importantly, in weighted graphs, the eigenvalues of L
are sensitive to weights of the edges in an edge cut set.
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

7. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Properties of λ2(L)
1 λ2(LΛ) is very sensitive to
weights of edges which
“connect” distinct
components.
2 The gradient of λ2(LΛ) w.r.t
the elements of L can be
analytically expressed.
3 Numerical computation of the
gradient of λ2(LΛ) also tends
to be accurate even for large
LΛ matrices, making it ideal
for numerical optimization
algorithms.
−0.2 −0.1 0.0 0.1 0.2
−1.00
−0.75
−0.50
−0.25
0.00
0.25
0.50
0.75
1.00
0 1
2
3
4
5
6
7
8
9
10
11
12 13
14
15
16
17
18 19
0.2 0.4 0.6 0.8 1.0
weight of the linking edge
0.0025
0.0050
0.0075
0.0100
0.0125
0.0150
0.0175
secondeigenvalue
linking edge
insider edge
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

8. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
λ2(L) as a function of vehicle position
1 λ2(L) gets smaller when
the vehicle approaches the
critical edge.
2 If fact, the gradient
x λ2(L) consistently
points away from the
central edge.
3 In this choice of the weight
function, the value is
independent of the position
x, given x is “far” from the
critical edge.
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
0
2
4
6
8
0.000
0.005
0.010
0.015
0.020
0.025
0.030
0.035
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

9. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
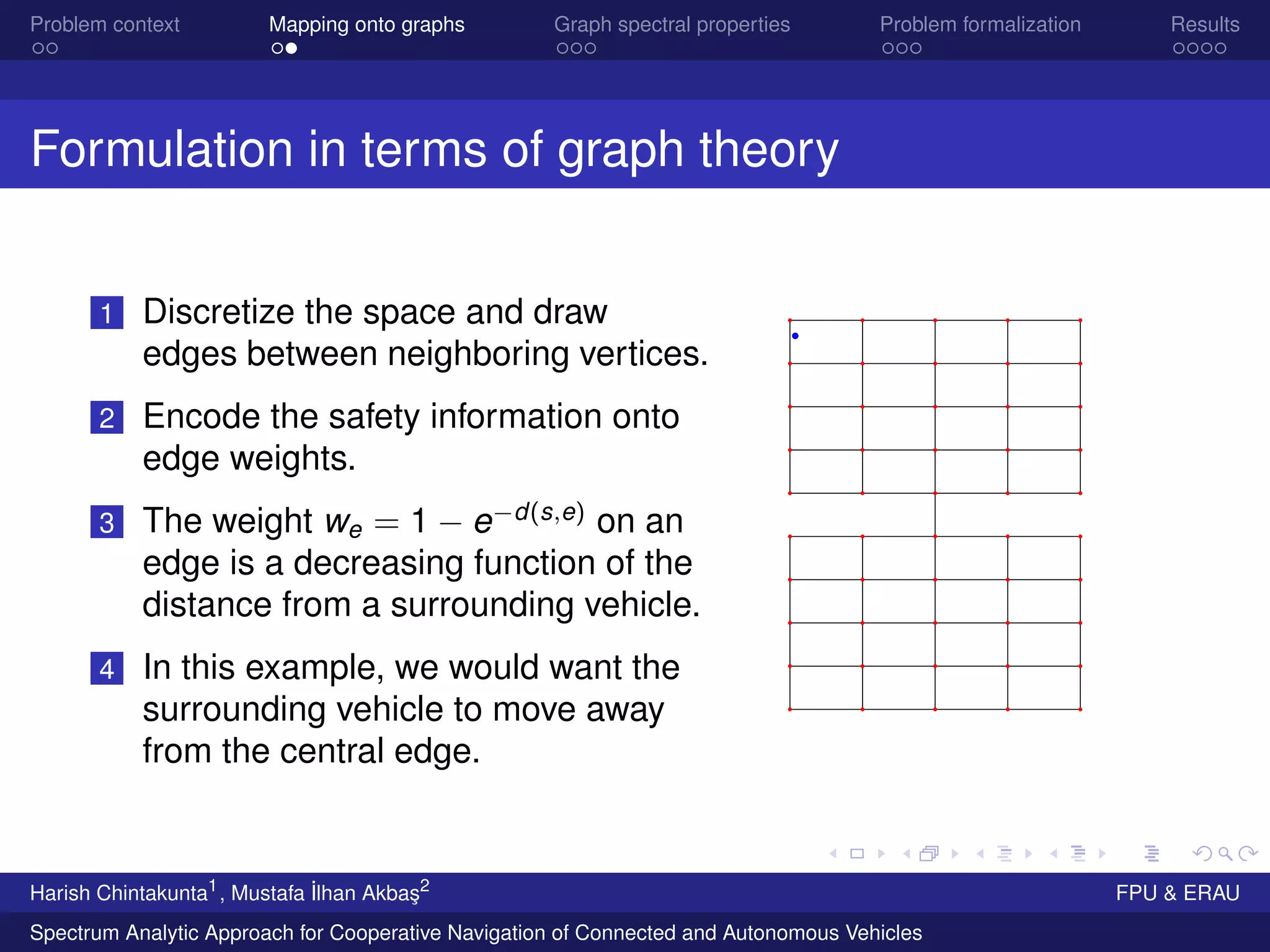
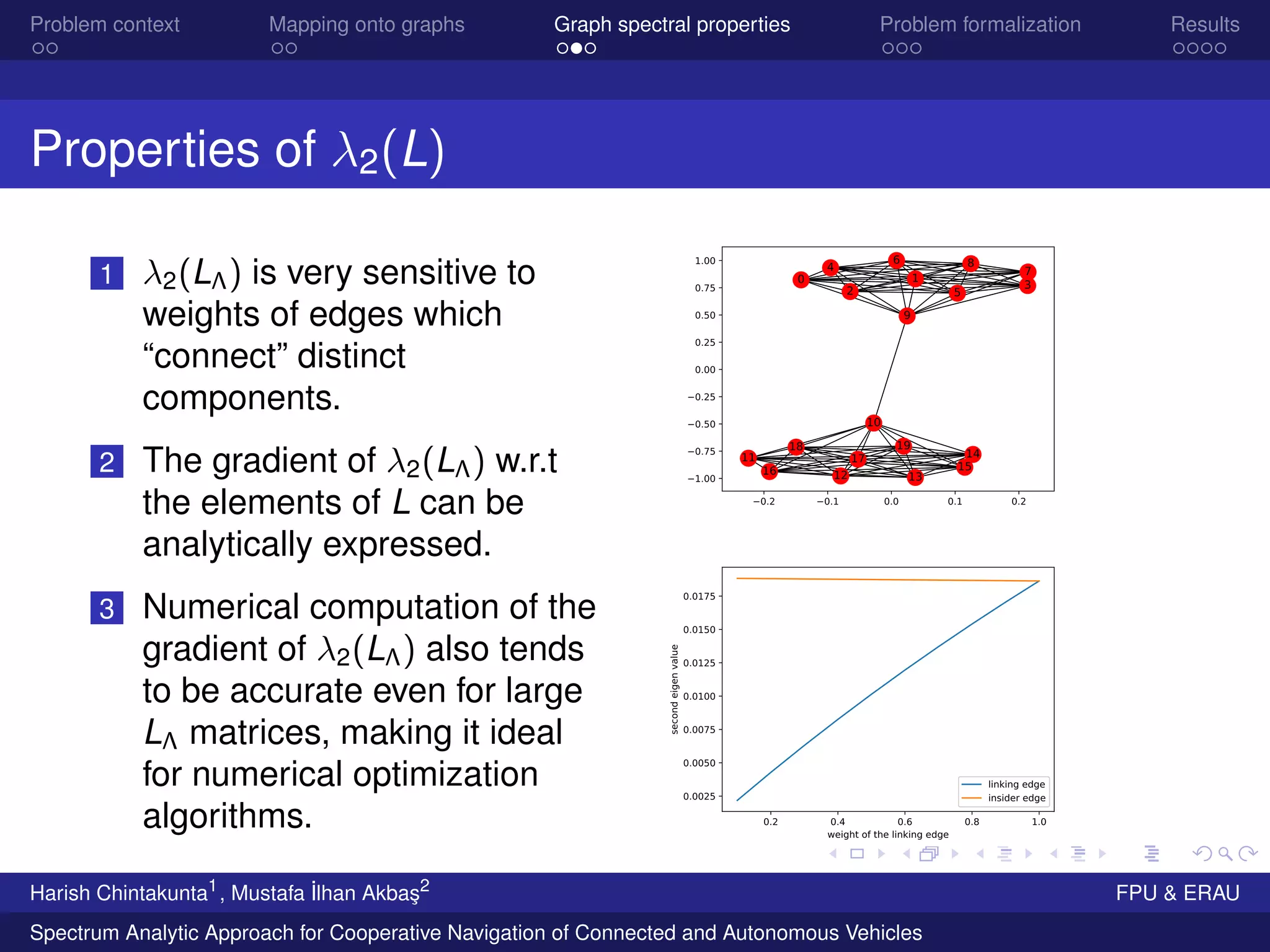
Putting things together
Construct a graph G = (V, E) with discretized points in the
space as vertices, and edges between vertices in a
geometrical neighborhood.
Λ : configuration of the obstacles.
Assign weights wΛ : E → [0, 1], where wΛ(e) is a function
of distances between the edge and all other obstacles.
LΛ((ui, uj)) =
−wΛ((ui, uj)), ui = uj
uk =ui
wΛ((ui, uk )), ui = uj
The second eigenvalue λ2(LΛ) will serve as a good
measure for connectivity.
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

10. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Framing as an optimization problem
EV
SV
0 1 2 3 4 5 6 7 8
0.00
0.25
0.50
0.75
1.00
1.25
1.50
1.75
2.00
0
1
2
3
4
5
6
7
8
0 1 2 3 4 5 6 7 8 0.000.250.500.751.001.251.501.752.00
0
1
2
3
4
5
6
7
8
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

11. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Solution to optimization problem
1 The acceleration functions of the surrounding vehicles are
optimized to provide a safe path to the EV.
2 Providing a safe path translates to
“Make a stronger connected component”
3 The above objective is achieved by:
{a∗
i (t)} = arg max{ai(t)} λ2(LΛ)
s.t. Safety and boundary constraints on Λ
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

12. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Results
Movement without control:
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
Movement with control:
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
0 5 10
0
1
2
Optimized acceleration functions:
0 1 2 3 4 5 6 7 8
−0.3
−0.2
−0.1
0.0
0.1
0.2
0.3
x-acceleration
y-acceleration
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

13. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Conclusions
1 The “safety” of the situation with respect to navigation of
EV in captured by λ2(L) of a suitably constructed graph.
2 The configuration of the surrounding vehicles is altered to
improve the safety measure.
3 The alteration of the surrounding vehicle configuration is
achieved by moving them along the gradient direction of
the safety measure.
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

14. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Future directions
1 Distributed algorithms to compute the gradient of the
configuration.
2 Statistical analysis in a realistic traffic situation.
3 Deeper understanding of the theoretical aspects of Fiedler
vector in the context of optimal cooperative driving.
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles

15. Problem context Mapping onto graphs Graph spectral properties Problem formalization Results
Thank you!!
Harish Chintakunta1
, Mustafa ˙Ilhan Akba¸s2
FPU & ERAU
Spectrum Analytic Approach for Cooperative Navigation of Connected and Autonomous Vehicles