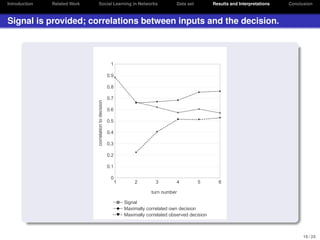
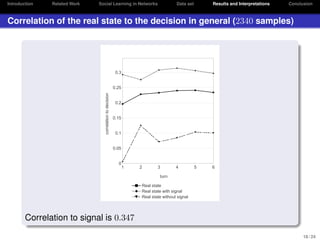
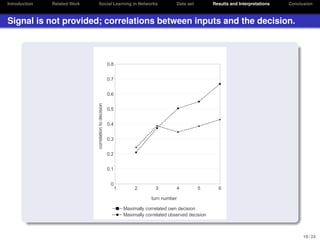
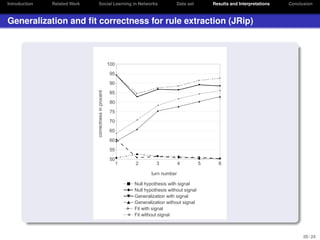
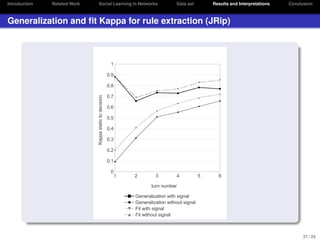
The document discusses social learning in networks, focusing on extracting deterministic rules from human behavior in economic experiments. It highlights the contrast between traditional economic theories and data-driven approaches, illustrating how human decision-making deviates from rational expectations. The authors present findings on correlations between signals and decisions, emphasizing the potential of data mining and machine learning techniques for understanding human behavior in economic contexts.

1. Social Learning in Networks:
Extraction of Deterministic Rules
Rustam Tagiew1 , Dmitry Ignatov2 , Fadi Amroush3
2
1
Qlaym GmbH, Dusseldorf, Germany
¨
National Research University Higher School of Economics, Moscow, Russia
3
Granada Lab of Behavioral Economics (GLOBE), Granada, Spain
EEML 2013 at IEEE ICDM 2013
Dallas, TX, USA

2. 1
Introduction
2
Related Work
3
Social Learning in Networks
4
Data set
5
Results and Interpretations
6
Conclusion

3. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Economics and Data Mining – Same Goal, Different Mindsets
The goal regarding human intercation
Hinting causalitities, Prediction of outcomes
Mindset of Economists
As in physics, theoretical considerations lead to a model, whose
parameters are then fitted to the data
Mindset of Data Miners
A set of validated relations is derived from the data for later
theoretical considerations
3 / 24

4. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Once standard Economic Theory
The “Homo Economicus” Assumption
Humans are egoistic and rational
... and this is a common knowledge
The preferences are settled by amounts of money
Don’t confuse it with Game Theory
Game Theory is just neutral math to use,
if preferences are known and players are rational
4 / 24

5. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Failure led to Experimental Economics
Unsurprisingly, humans are
... neither throughout egoistic
... no correct in reasoning to be rational.
They therefore deviate from game theoretic equilibria
but in quite predictable ways.
Data situation
Economists continue to conduct laboratory experiments
Excessive field data available since
Orwellian nightmare became reality
5 / 24

6. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Data used in this paper
Same data, different mindset
Choi et al., 2012
“Social learning in networks: quantal response equilibrium
analysis of experimental data”
Tagiew et al., 2013
“Social learning in networks: extraction of deterministic rules”
6 / 24

7. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Related work
Choi et al., 2012
Quantal Response Equilibrium (QRE)
“trembling-hand” essentially “delutes” game theoretic equilibria
P (action1,i ) =
eλ
actionk
j∈Actions2
eλ
P (action2,j )u1 (action1,i ,action2,j )
k∈Actions1
P (action2,j )u1 (action1,k ,action2,j )
λ → ∞ results in the game theoretic equilibrium
λ → 0 results in random choice
7 / 24

8. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Related work
Tagiew, 2012
The two cases of behavior modelling in games
Participation: payoff maximization
→ Non-deterministic models
Spectator: correctness maximization
→ Deterministic models
Performance
Cross-validation results of support vector machine based
deterministic models outperformed related work on two data sets
8 / 24

9. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Social Learning in Networks – Game rules
Social Learning is the process of acquiring knowledge by observation
of other players’ turns.
3 chosen network types of observation for 3 players
A
A
B
Complete
C
B
A
C
Circle
B
C
Star
9 / 24

10. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Social Learning in Networks – Game rules
Further Details
The hidden variable is either white (1) or red (-1)
(state of the world)
If a players’ action matches the hidden variable,
(s)he gets on average $0.5 payoff
A turn is a simultaneous action by 3 players,
after what actions can be observed
A round consists of 6 subsequent turns
At start of a round, every player might secretly get a signal,
2
which equals the hidden variable in of cases
3
A group of 3 players completes 15 rounds at a stretch
10 / 24

11. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Social Learning in Networks – Game rules
Information levels
full: signals are always sent
2
high: signals are sent in of cases
3
1
low: signals are sent in of cases
3
11 / 24

12. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Data Set
Number of subjects’ groups for 9 game configurations.
Information/
Network type
Complete
Circle
Star
Low
High
Full
6
5
6
5
6
6
6
6
6
Total Number of Human Decisions
3 ∗ 6 ∗ 15 = 270 times the sum of the table results 14040
12 / 24

13. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Signal is not provided; first turn (747 samples)
Bias towards −1
Information/
Network type
complete
star
circle
sum
low
high
sum
62%
67%
53%
61%
69%
55%
52%
59%
64%
64%
53%
60%
13 / 24

14. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Signal is provided; first turn (1593 samples)
Deviation from Signal
Player’s decision significantly correlates to signal only (0.883)
Signal/
Decision
−1
1
−1
1
757
42
51
743
5.8% deviation from rational choice
(first round is not significantly lower)
Either undergrad students at New York University
failed at elementary math or they were aware of others’ payoffs
14 / 24

15. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
“Awareness of others’ payoffs”
Brosnan and de Waal, Nature, 2007
Capuchin monkey experiment
YouTube link
15 / 24

16. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Signal is provided; correlations between inputs and the decision.
1
0.9
correlation to decision
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
2
3
4
5
6
turn number
Signal
Maximally correlated own decision
Maximally correlated observed decision
16 / 24

17. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Is the sabotage successful?
The equilibrium in full information complete network
1th turn: Copy the signal!
2-6 turns: Copy the last turns’ median!
The deviation makes it futile to observe others (270 samples)
Median’s correctness drops from 74% to 68%
Median and signal equally correlate with state
17 / 24

18. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Correlation of the real state to the decision in general (2340 samples)
0.3
correlation to decision
0.25
0.2
0.15
0.1
0.05
0
1
2
3
4
5
6
turn
Real state
Real state with signal
Real state without signal
Correlation to signal is 0.347
18 / 24

19. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Signal is not provided; correlations between inputs and the decision.
0.8
0.7
correlation to decision
0.6
0.5
0.4
0.3
0.2
0.1
0
1
2
3
4
5
6
turn number
Maximally correlated own decision
Maximally correlated observed decision
19 / 24

20. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Generalization and fit correctness for rule extraction (JRip)
100
95
correctness in procent
90
85
80
75
70
65
60
55
50
1
2
3
4
5
6
turn number
Null hypothesis with signal
Null hypothesis without signal
Generalization with signal
Generalization without signal
Fit with signal
Fit without signal
20 / 24

21. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Generalization and fit Kappa for rule extraction (JRip)
1
0.9
Kappa static to decision
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
2
3
4
5
6
turn number
Generalization with signal
Generalization without signal
Fit with signal
Fit without signal
21 / 24

22. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Example of rule extraction
IF (Own decision in turn 3 = -1)
& (Own decision in turn 4 = -1) THEN -1
ELSEIF (Own decision in turn 3 = -1)
& (Signal = -1) & (Player = B) THEN -1
ELSEIF (Own decision in turn 3 = -1)
& (1th observed in turn 4 = -1)
& (GType = star) THEN -1
ELSEIF (Own decision in turn 4 = -1)
& (Own decision in turn 2 = 1)
& (Player = C) & (Round <= 7)
& (Observed in turn 2 = -1) THEN -1
ELSEIF (Observed in turn 3 = -1)
& (Own decision in turn 3 = -1)
& (Round <= 7) & (Round >= 5)
& (Signal = -1) THEN -1
ELSEIF (Own decision in turn 4 = -1)
& (Observed in turn 3 = -1)
& (Player = B) THEN -1
ELSEIF (Own decision in turn 4 = -1)
& (Own decision in turn 1 = -1)
& (Player = C) THEN -1
ELSE 1
22 / 24

23. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Conclusion
Strong hint of pugnacious behavior
Deterministic rules are able to generalize human behavior
23 / 24

24. Introduction
Related Work
Social Learning in Networks
Data set
Results and Interpretations
Conclusion
Future work
Collecting more data from Experimental Economics domain on a
Web portal
Applying other Data Mining & Machine Learning techniques for
Economics and Social Sciences data concerning human
behavior
In particular emergent sequential patterns seems to be a good
tool for Game Data Mining since we deal with sequences of
actions and their outcomes
Collaboration with other research teams working in Experimental
Economics and Game Theory potentially interested in DM&ML
methods
24 / 24