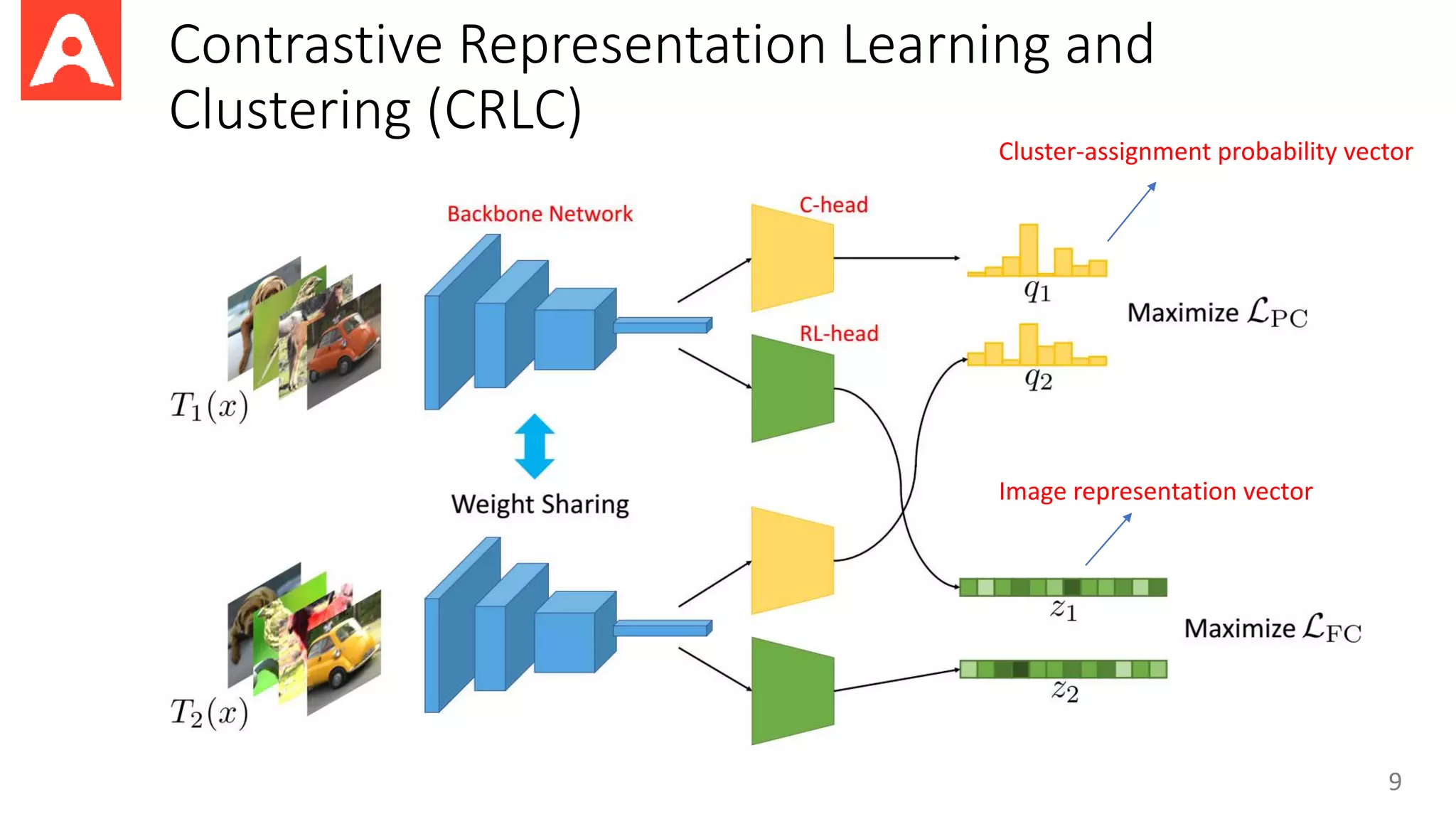
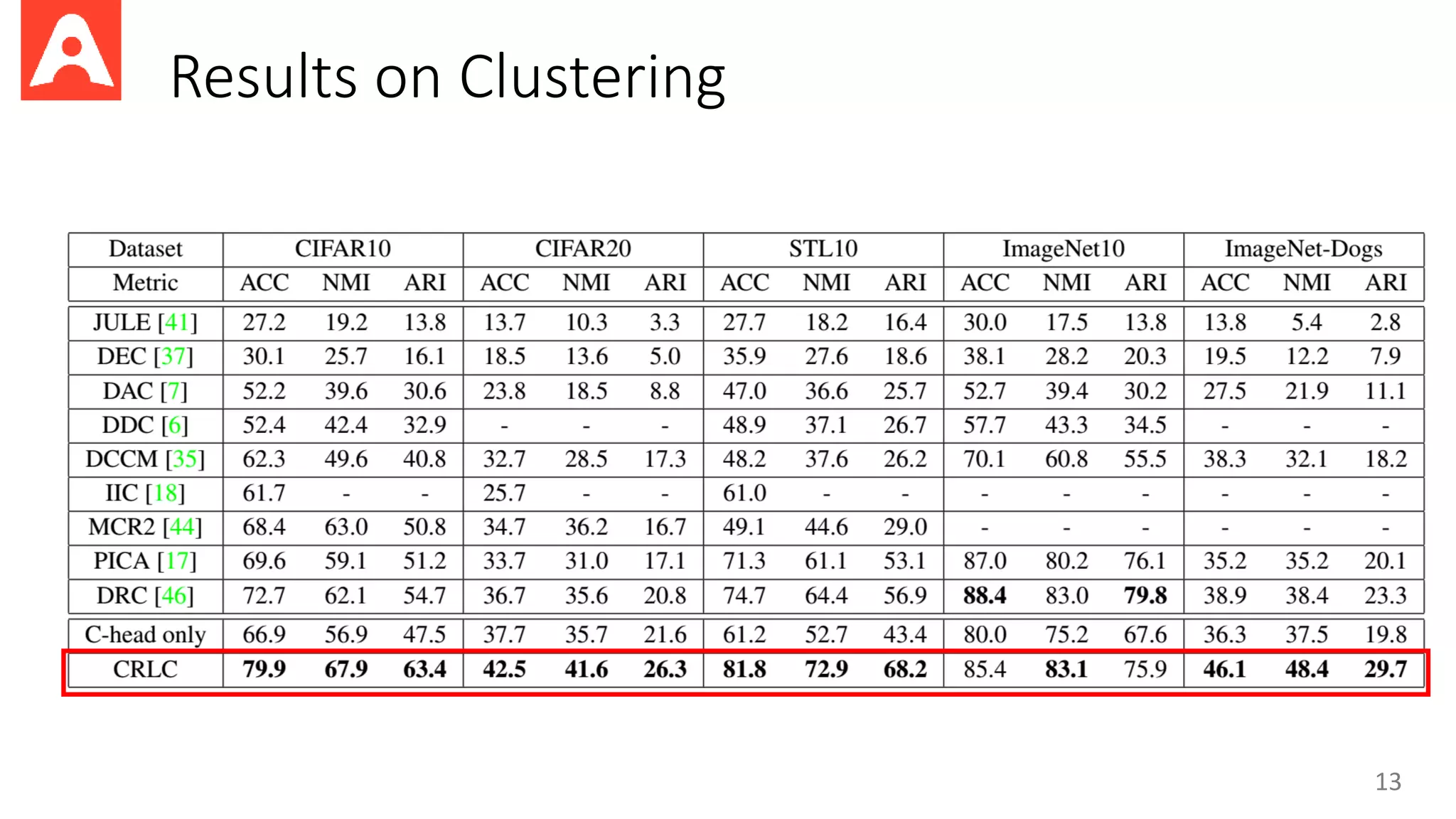
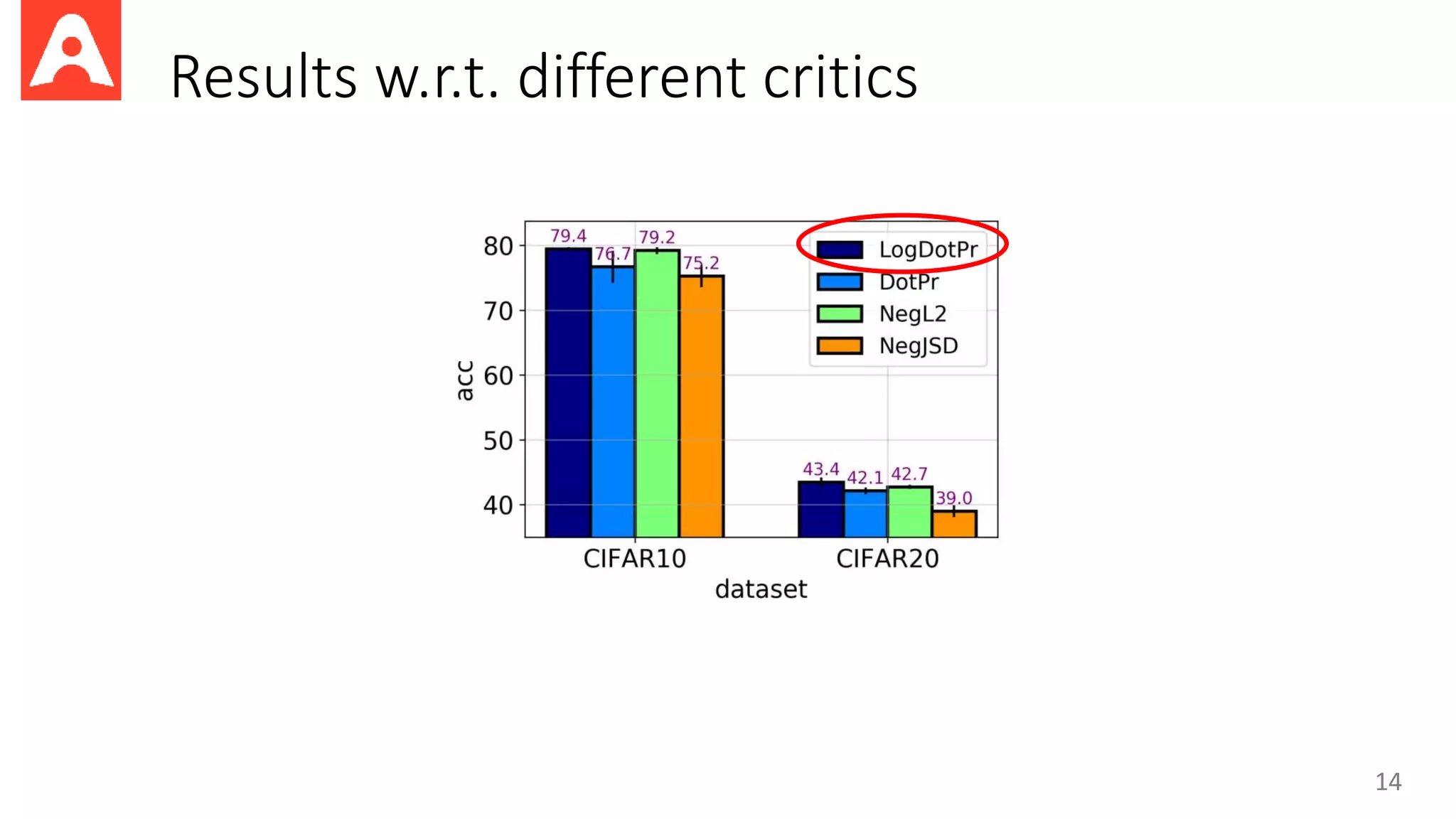
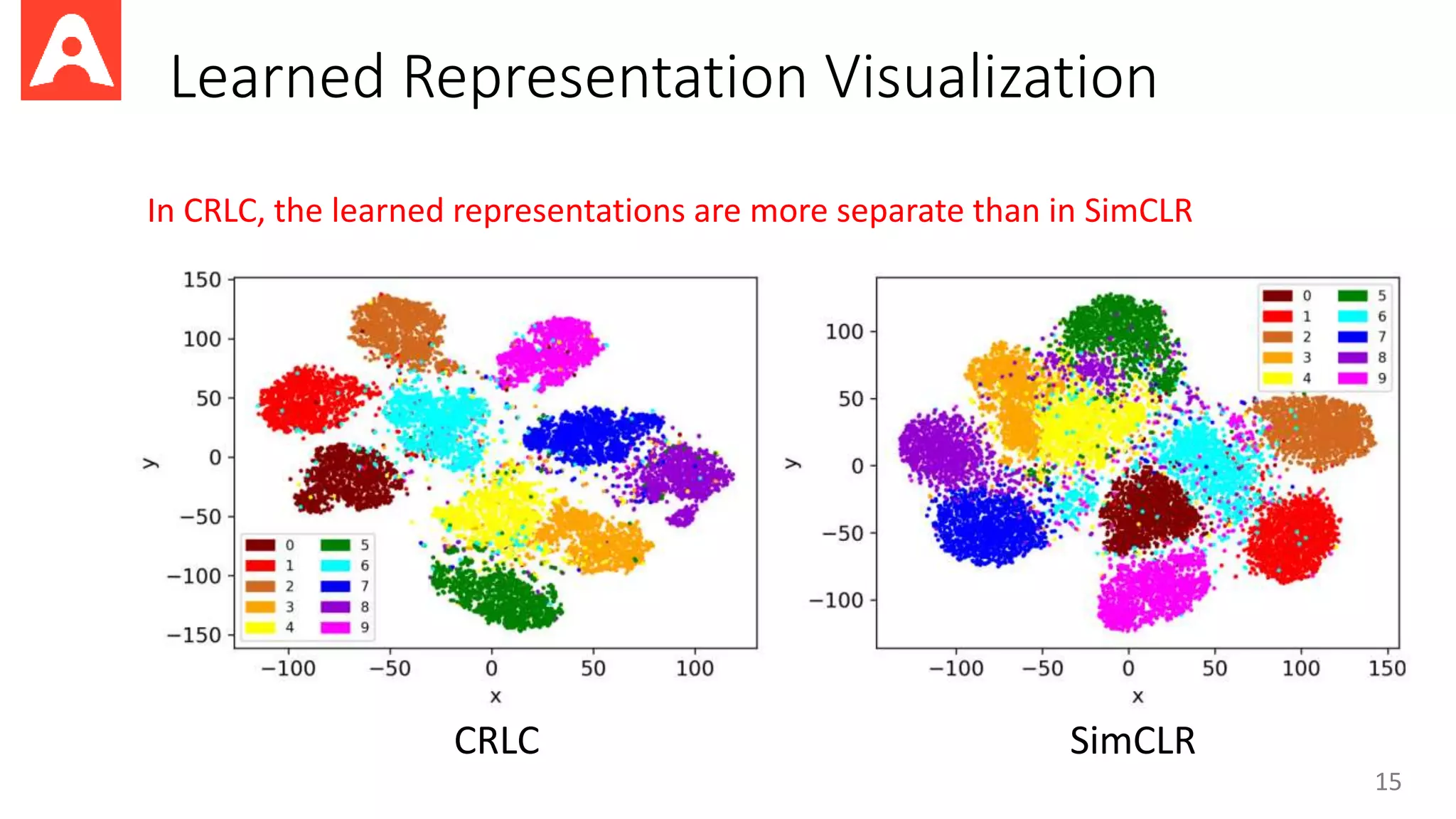
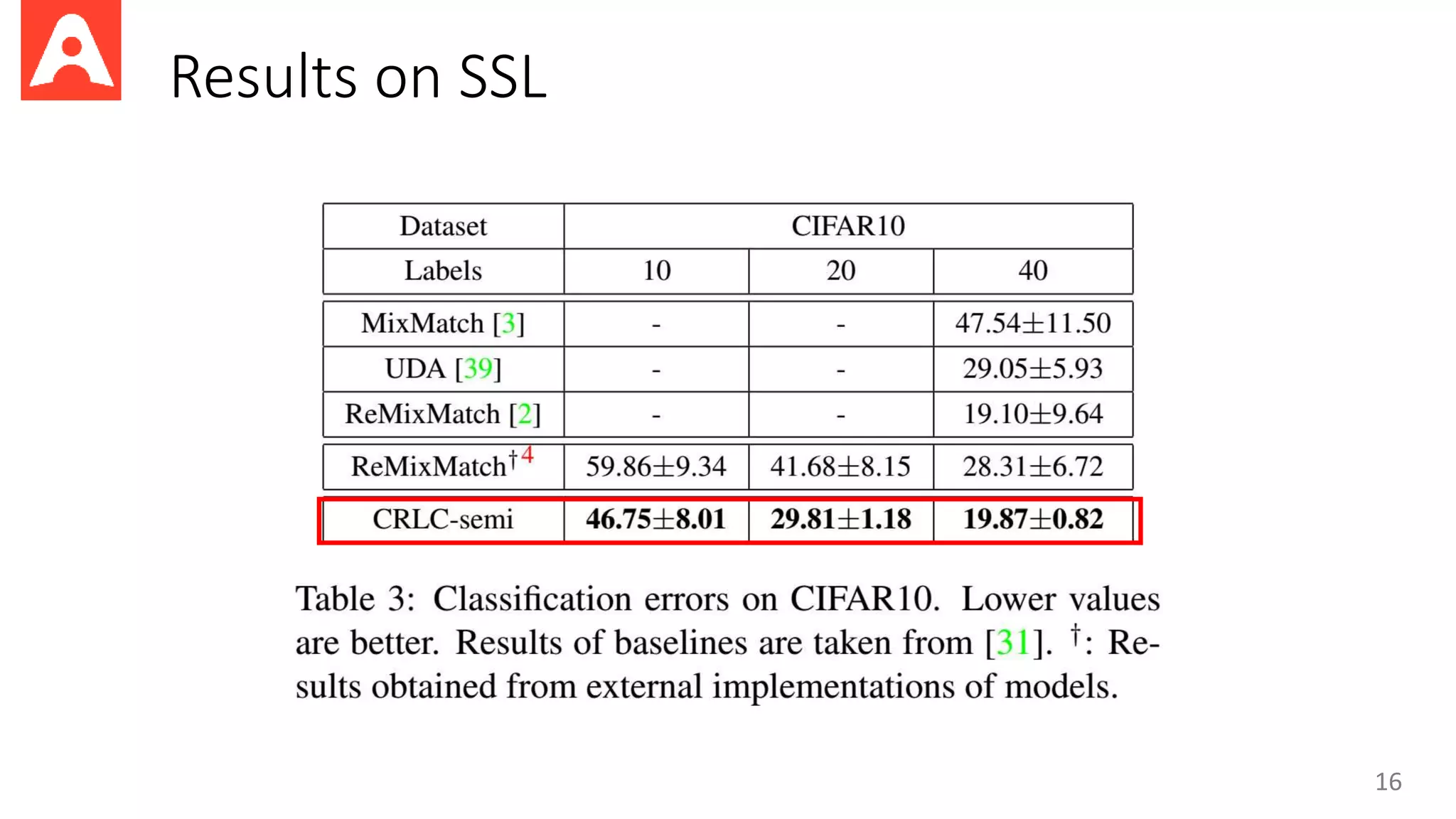
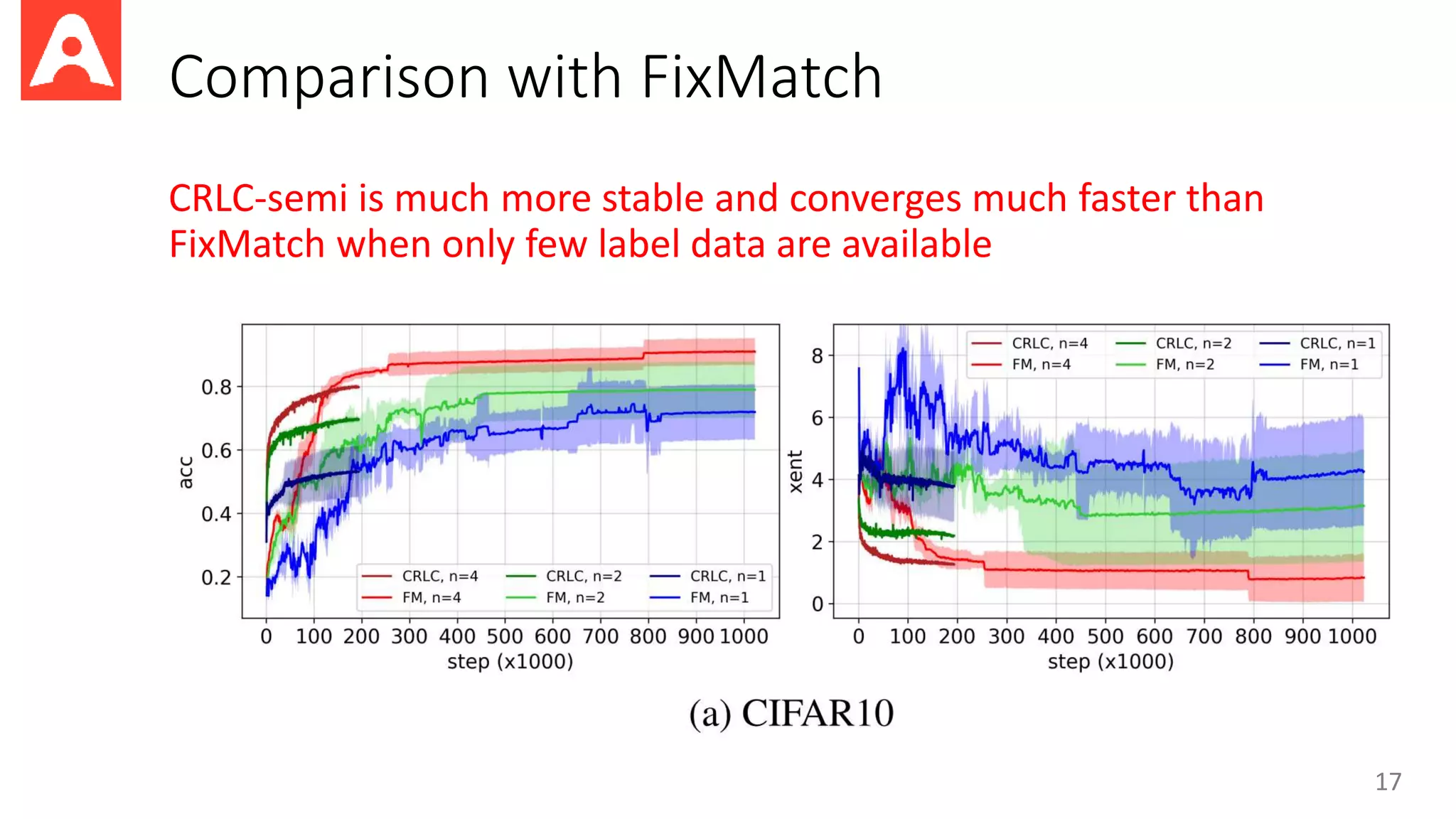
This document proposes a new method called Contrastive Representation Learning for Clustering (CRLC) that applies the principle of maximizing mutual information across views to learn cluster-level and instance-level semantics for unsupervised image clustering. CRLC trains an encoder to map images to a representation space by maximizing the agreement between the image representation and a cluster-assignment probability vector, using either cosine similarity or log-of-dot-product as the critic. This training loss functions to minimize a contrastive loss and learn discriminative representations. Experimental results show CRLC learns more separated representations than baselines and achieves better clustering and semi-supervised learning performance.

1. Clustering by Maximizing Mutual
Information Across Views
Kien Do, Truyen Tran, Svetha Venkatesh
Applied AI Institute (A2I2), Deakin University, Australia
1

2. Image Clustering Problem
2
The explosion of unlabelled data has led to the growing demand for unsupervised clustering

3. Clustering Assumptions
3
Inter-cluster distance
should be large
Intra-cluster distance
should be small

4. Existing Clustering Methods
4
Enc Dec
Clustering the latent code
Autoencoder-based methods (e.g., DCN, VaDE, DGG)
DCN [1]
Closer in the latent space of the AE
The latent should only capture semantic information from the input
[1] Towards k-means-friendly spaces: Simultaneous deep learning and clustering, Yang et al., ICML 2017

5. Existing Clustering Methods (cont.)
5
IIC [1]
Methods that only use the cluster-assignment probability (e.g., IIC, PICA)
Problem: May not capture enough useful
information from data => over-clustering is
often required.
[1] Invariant Information Clustering for Unsupervised Image Classification and Segmentation, Ji et al., ICCV 2019

6. Motivation
• We need a method that can model the cluster-level and the instance-
level semantics.
• The InfoMax/Contrastive Learning principle can be applied to this
scenario.
6

7. Overview about InfoMax/Contrastive Learning
• A principle for learning view-invariant representations. These
representations often capture the data semantics.
• The idea is maximizing the mutual information (MI) between 2
different views.
• Since direct computation of the MI is hard, we maximize its
variational lower bound instead.
7

8. The InfoNCE bound
• InfoNCE [1] is a lower bound of MI
• It is biased but has low variance
• Maximizing InfoNCE is equivalent to minimizing a contrastive loss:
8
[1] On Variational Bounds of Mutual Information, Poole et al., ICML 2019
is a “critic” measuring the similarity between and

9. Contrastive Representation Learning and
Clustering (CRLC)
9
Image representation vector
Cluster-assignment probability vector

10. Training Loss
10
where:

11. Choosing an optimal critic
• A critic is optimal ( ) if it leads to the tightest InfoNCE bound.
• It can be shown that
• In continuous cases, cosine similarity is the optimal critic
• In discrete cases, “log-of-dot-product” is the optimal critic
11

12. A Simple extension to Semi-supervised Learning
12
Assume that we also have access to some labeled set . The training loss is:

13. Results on Clustering
13

14. Results w.r.t. different critics
14

15. Learned Representation Visualization
15
CRLC SimCLR
In CRLC, the learned representations are more separate than in SimCLR

16. Results on SSL
16

17. Comparison with FixMatch
CRLC-semi is much more stable and converges much faster than
FixMatch when only few label data are available
17

18. 18
Thank you for your attention!