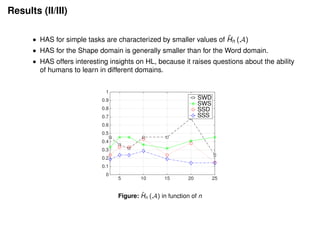
1) The document proposes measuring human learning ability through complexity measures like Rademacher complexity and algorithmic stability, which are commonly used to analyze machine learning algorithms.
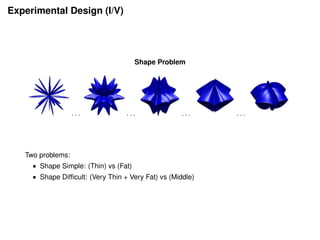
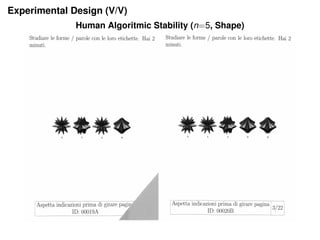
2) An experiment was designed to estimate average human Rademacher complexity and algorithmic stability for students on different types of tasks (shape and word problems).
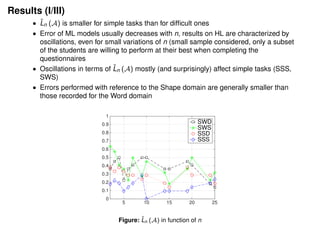
3) The results showed that human algorithmic stability provided more useful insights into human learning than Rademacher complexity, as it does not require fixing a function class or assuming optimal performance like Rademacher complexity does.









![Rademacher Complexity7
Rademacher Complexity (RC) is a
now-classic measure:
ˆRn(F) =
1
m
m
j=1
1− inf
f∈F
2
n
n
i=1
(f, (X
j
i
, σ
j
i
))
σ
j
i
(with i ∈ {1, . . . , n} and j ∈ {1, . . . , m})
are ±1 valued random variable for which
P[σ
j
i
= +1] = P[σ
j
i
= −1] = 1/2.
7
P. L. Bartlett and S. Mendelson. Rademacher and gaussian complexities: Risk bounds and structural results.
The Journal of Machine Learning Research, 3:463-482, 2003.](https://image.slidesharecdn.com/presentationv2-161202101722/85/Presentation-v2-10-320.jpg)