This document discusses the vulnerability of machine learning models to privacy attacks, specifically focusing on membership inference attacks that exploit overfitting to the training dataset. It asserts that causal models offer stronger differential privacy guarantees than traditional associational models due to their better generalization across different data distributions, thus demonstrating lower attack accuracy against membership inference. The authors empirically validate their claims across multiple datasets, illustrating that causal models significantly mitigate privacy risks without compromising prediction accuracy.

1. Alleviating Privacy Attacks via
Causal Learning
Shruti Tople, Amit Sharma, Aditya V. Nori
Microsoft Research
https://arxiv.org/abs/1909.12732
https://github.com/microsoft/robustdg

2. Motivation: ML models leak information
about data points in the training set
Neural
Network
TrainingHealth Records
(HIV/AIDS
patients)
ML-as-a-service
Member of
Train Dataset
Non-member
Membership Inference Attacks
[SP’17][CSF’18][NDSS’19][SP’19]

3. The likely reason is overfitting
Output
85%
Output
95%
Overfitting to
dataset
• Neural networks or associational models
overfit to the training dataset
• Membership inference adversary exploits
differences in prediction score for training and
test data [CSF’18]

4. Overfitting to
distribution
The likely reason is overfitting
• Neural networks or associational models
overfit to the training dataset
• Membership inference attacks exploit
differences in prediction score for training and
test data [CSF’18]
• Privacy risk can increase when model is
deployed to different distributions
• E.g., Hospital in one region shares the model to
other regions
Output
85%
Output
95%
Overfitting to
dataset
Output
75%
Poor generalization across distributions exacerbates
membership inference risk.

5. Can causal ML
models help?

6. Can causal ML models help?
Contributions
1. Causal models provide stronger (differential) privacy guarantees than
associational models.
• Due to their better generalizability on new distributions.
2. And hence are more robust to membership inference attacks.
• As the training dataset size → ∞, membership inference attack’s accuracy drops to a
random guess.
3. We empirically demonstrate privacy benefits of causal models across 5 datasets.
• Associational models exhibit up to 80% attack accuracy whereas causal models exhibit
attack accuracy close to 50%.
Causal
Learning
Privacy

7. Disease
Severity
Background: Causal Learning
𝒀
Blood
Pressure
Heart
Rate
𝑿 𝒑𝒂𝒓𝒆𝒏𝒕 𝑿 𝒑𝒂𝒓𝒆𝒏𝒕
𝑿 𝟏 𝑿 𝟐
Weight Age
Use a structural causal model (SCM) that defines what
conditional probabilities are invariant across different
distributions [Pearl’09].

8. Background: Causal Learning
Use a structural causal model (SCM) that defines what
conditional probabilities are invariant across different
distributions [Pearl’09].
Causal Predictive Model: A prediction model based only
on the parents of the outcome Y.
What if SCM is not known? Learn an invariant feature
representation across distributions [ABGD’19, MTS’20].
For ML models, causal learning can be useful for
fairness [KLRS’17]
explainability [DSZ’16, MTS’19]
privacy [this work]
Disease
Severity
𝒀
Blood
Pressure
Heart
Rate
𝑿 𝒑𝒂𝒓𝒆𝒏𝒕 𝑿 𝒑𝒂𝒓𝒆𝒏𝒕
𝑿 𝟏 𝑿 𝟐
Weight Age

9. 𝒀
𝑋𝑆0 𝑋 𝑃𝐴
𝑋𝑆2
𝑋𝑆1
𝑋 𝐶𝐻
𝑋𝑐𝑝
Intervention
Why is a model based on causal parents
invariant across data distributions?

10. Why is a model based on causal parents
invariant across data distributions?
𝒀
𝑋𝑆0 𝑋 𝑃𝐴
𝑋𝑆2
𝑋𝑆1
𝑋 𝐶𝐻
𝑋𝑐𝑝
Intervention
𝒀
𝑋𝑆0 𝑋 𝑃𝐴
𝑋𝑆2
𝑋𝑆1
𝑋 𝐶𝐻
𝑋𝑐𝑝
𝑃(𝑌|𝑋 𝑃𝐴) is invariant across different distributions, unless there is a
change in true data-generating process for Y.

11. Result 1: Worst-case out-of-distribution error of a
causal model is lower than an associational model.

12. For any model ℎ, and 𝑃∗ such that 𝑃∗ 𝑌 𝑋 𝑃𝐴 = 𝑃(𝑌|𝑋 𝑃𝐴),
In-Distribution Error (IDE)= 𝐈𝐃𝐄 𝐏 𝒉, 𝒚 = 𝐋 𝑷 𝒉, 𝒚 − 𝐋 𝑺∼P(𝒉, 𝒚)
Expected loss on the same distribution as the train data
Out-of-Distribution Error (ODE)=𝐎𝐃𝐄 𝐏,𝐏∗ 𝒉, 𝒚 = 𝐋 𝑷∗ 𝒉, 𝒚 − 𝐋 𝑺∼P 𝒉, 𝒚
Expected loss on a different distribution 𝑃∗
than the train data
Result 1: Worst-case out-of-distribution error of a
causal model is lower than an associational model.

13. For any model ℎ, and 𝑃∗ such that 𝑃∗ 𝑌 𝑋 𝑃𝐴 = 𝑃(𝑌|𝑋 𝑃𝐴),
In-Distribution Error (IDE)= 𝐈𝐃𝐄 𝐏 𝒉, 𝒚 = 𝐋 𝑷 𝒉, 𝒚 − 𝐋 𝑺∼P(𝒉, 𝒚)
Expected loss on the same distribution as the train data
Out-of-Distribution Error (ODE)=𝐎𝐃𝐄 𝐏,𝐏∗ 𝒉, 𝒚 = 𝐋 𝑷∗ 𝒉, 𝒚 − 𝐋 𝑺∼P 𝒉, 𝒚
Expected loss on a different distribution 𝑃∗
than the train data
Proof Idea. Simple case: Assume 𝑦 = 𝑓(𝒙) is deterministic.
𝐎𝐃𝐄 𝐏,𝐏∗ 𝒉 𝐜, 𝒚 ≤ 𝐈𝐃𝐄 𝐏(𝒉 𝒄, 𝒚) + 𝒅𝒊𝒔𝒄 𝐋 𝑷, 𝑷∗
Discrepancy
b/w 𝑷 and 𝑷∗
distributions
Causal Model
Result 1: Worst-case out-of-distribution error of a
causal model is lower than an associational model.

14. For any model ℎ, and 𝑃∗ such that 𝑃∗ 𝑌 𝑋 𝑃𝐴 = 𝑃(𝑌|𝑋 𝑃𝐴),
In-Distribution Error (IDE)= 𝐈𝐃𝐄 𝐏 𝒉, 𝒚 = 𝐋 𝑷 𝒉, 𝒚 − 𝐋 𝑺∼P(𝒉, 𝒚)
Expected loss on the same distribution as the train data
Out-of-Distribution Error (ODE)=𝐎𝐃𝐄 𝐏,𝐏∗ 𝒉, 𝒚 = 𝐋 𝑷∗ 𝒉, 𝒚 − 𝐋 𝑺∼P 𝒉, 𝒚
Expected loss on a different distribution 𝑃∗
than the train data
Proof Idea. Simple case: Assume 𝑦 = 𝑓(𝒙) is deterministic.
𝐎𝐃𝐄 𝐏,𝐏∗ 𝒉 𝐜, 𝒚 ≤ 𝐈𝐃𝐄 𝐏(𝒉 𝒄, 𝒚) + 𝒅𝒊𝒔𝒄 𝐋 𝑷, 𝑷∗
𝐎𝐃𝐄 𝐏,𝐏∗ 𝒉 𝒂, 𝒚 ≤ 𝐈𝐃𝐄 𝐏 𝒉 𝒂, 𝒚 + 𝒅𝒊𝒔𝒄 𝐋 𝑷, 𝑷∗
+ 𝐋 𝑷∗(𝒉 𝒂,𝑷
𝑶𝑷𝑻
, 𝒚)
⇒ max
𝐏∗
𝐎𝐃𝐄𝐁𝐨𝐮𝐧𝐝 𝐏,𝐏∗ 𝒉 𝐜, 𝒚 ≤ max
𝐏∗
𝐎𝐃𝐄𝐁𝐨𝐮𝐧𝐝 𝐏,𝐏∗ 𝒉 𝒂, 𝒚
Discrepancy
b/w 𝑷 and 𝑷∗
distributions
Optimal 𝒉 𝒂 on P is
not optimal on 𝑷∗
Causal Model
Assoc. Model
Result 1: Worst-case out-of-distribution error of a
causal model is lower than an associational model.

15. And better generalization results in lower
sensitivity for a causal model
Sensitivity: If a single data point 𝒙, 𝑦 ∼ 𝑃∗ is added to the train
dataset 𝑆 to create 𝑆′, how much does the learnt model h 𝑆
min
change?
Since the optimal causal model is the same across all 𝑃∗
, adding
any 𝒙, 𝑦 ∼ 𝑃∗ has less impact on a trained causal model.
Sensitivity for a causal
model
Sensitivity for an
associational model

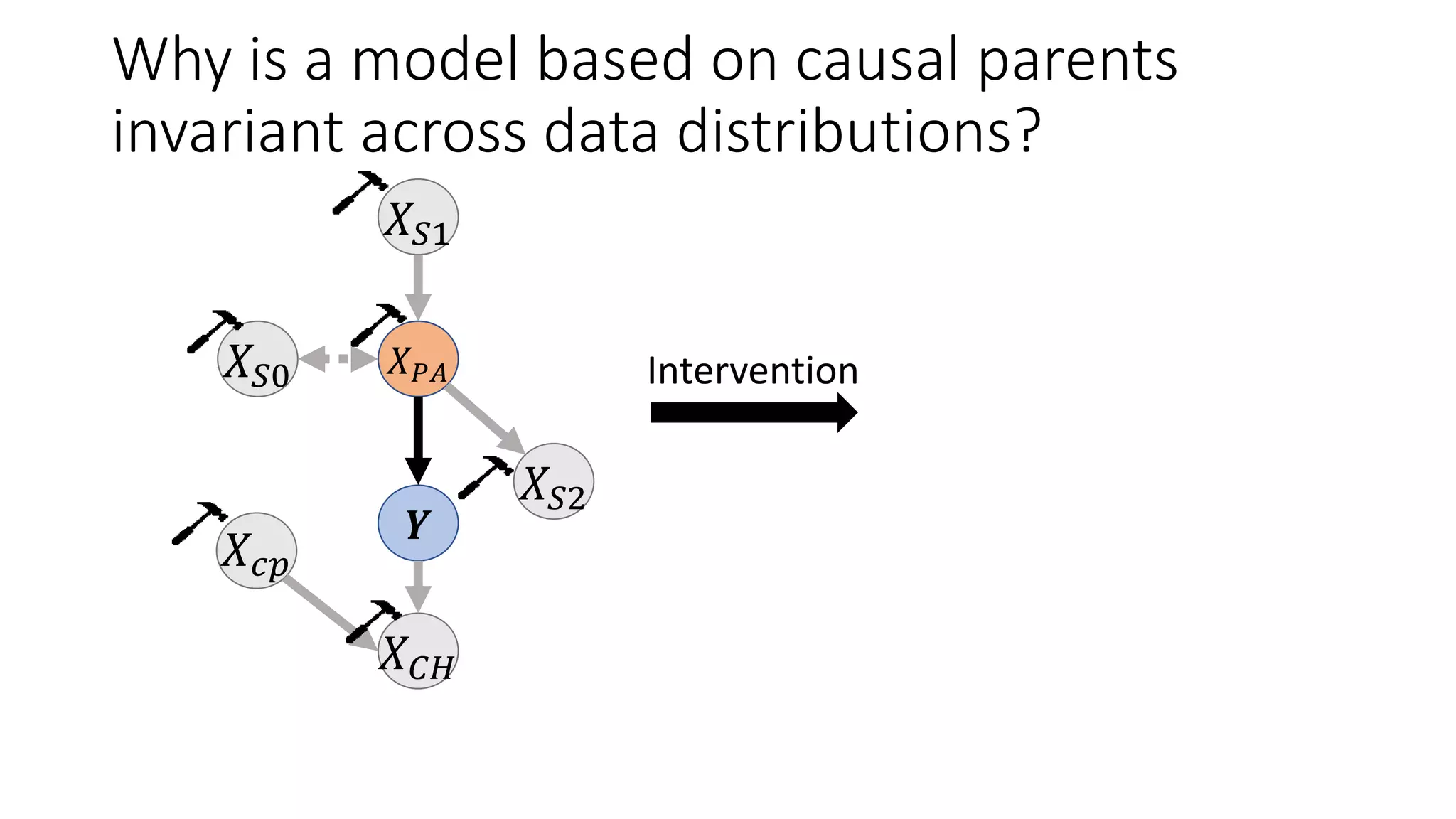
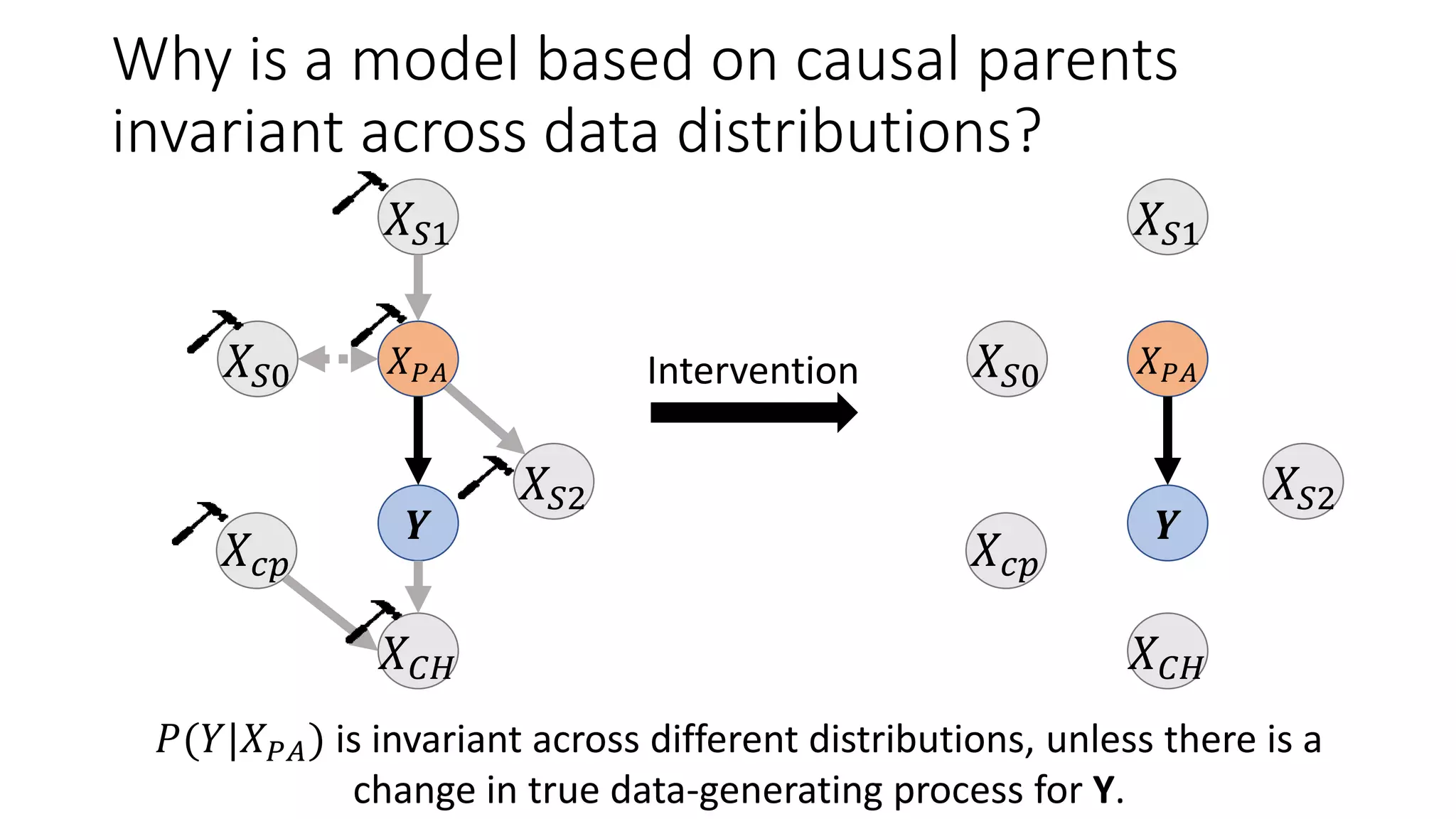
16. Main Result: A causal model has stronger
Differential Privacy guarantees
Let M be a mechanism that returns a ML model trained over dataset 𝑆, M(𝑆) = ℎ.
Differential Privacy [DR’14]: A learning mechanism M satisfies 𝜖-differential
privacy if for any two datasets, 𝑆, 𝑆′ that differ in one data point,
Pr(M 𝑆 ∈𝐻)
Pr(M 𝑆′ ∈𝐻)
≤ 𝑒 𝜖.
(Smaller 𝜖 values provide better privacy guarantees)
Since lower sensitivity ⇒ lower 𝜖,
Theorem: When equivalent Laplace noise is added and models are trained on same
dataset, causal mechanism MC provides 𝜖 𝐶-DP and associational mechanism MA
provides 𝜖 𝐴-DP guarantees such that:
𝝐 𝒄 ≤ 𝝐 𝑨

17. Therefore, causal models are more robust to
membership inference (MI) attacks
Advantage of an MI adversary:
(True Positive Rate – False Positive Rate)
in detecting whether 𝑥 is from training dataset or not.
[From Yeom et al. CSF’18] Membership advantage of an adversary is bounded by
𝑒 𝜖
− 1.
Since the optimal causal models are the same for 𝑃 and 𝑃∗,
As 𝑛 → ∞, membership advantage of causal model → 0.
Theorem: When trained on the same dataset of size 𝑛, membership
advantage of a causal model is lower than the membership advantage for an
associational model.

18. Empirical
Evaluation

19. Goal: Compare MI attack accuracy between
causal and associational models
[BN] When true causal structure is known
Datasets generated from Bayesian networks: Child, Sachs, Water, Alarm
Causal model: MLE estimation based on Y’s parents
Associational model: Neural networks with 3 linear layers
𝑃∗: Noise added to conditional probabilities (uniform or additive)
[MNIST] When true causal structure is unknown
Colored MNIST dataset (Digits are correlated with color)
Causal Model: Invariant Risk Minimization that utilizes 𝑃 𝑌 𝑋 𝑃𝐴 is same across distributions [ABGD’19]
Associational Model: Empirical Risk Minimization using the same NN architecture
𝑃∗: Different correlations between color and digit than the train dataset
Attacker Model: Predict whether an input belongs to train dataset or not

20. [BN] With uniform noise, MI attack accuracy
for a causal model is near a random guess
80%
50%
For associational models, the attacker can guess membership in training set with 80% accuracy.

21. [BN-Child] With uniform noise, MI attack accuracy
for a causal model is near a random guess
80%
50%
For associational models, the attacker can guess membership in training set with 80% accuracy.
Privacy without loss in utility: Causal & DNN models achieve same prediction accuracy.

22. [BN-Child] MI Attack accuracy increases with
amount of noise for associational models, but
stays constant at 50% for causal models

23. [BN] Consistent results across all four datasets
High attack accuracy for associational
models when 𝑃∗
(Test2) has uniform noise.
Same classification accuracy between
causal and associational models.

24. [MNIST] MI attack accuracy is lower for invariant
risk minimizer compared to associational model
IRM model motivated by causal reasoning has 53% attack accuracy, close to random.
Associational model also fails to generalize: 16% accuracy on test set.
Model
Train
Accuracy
(%)
Test
Accuracy
(%)
Attack
Accuracy
(%)
Causal Model
(IRM)
70 69 53
Associational
Model (ERM)
87 16 66

25. Conclusion
• Established theoretical connection between causality and differential privacy.
• Demonstrated the benefits of causal ML models for alleviating privacy attacks,
both theoretically and empirically.
• Code available at https://github.com/microsoft/robustdg
Future work: Investigate robustness of causal models with other kinds of
adversarial attacks.
Causal
Learning
Privacy
thank you!
Amit Sharma
Microsoft Research

26. References
• [ABGD’19] Martin Arjovsky, Léon Bottou, Ishaan Gulrajani, and David Lopez-Paz. Invariant risk minimization. arXiv
preprint arXiv:1907.02893, 2019.
• [CSF’18] Yeom, S., Giacomelli, I., Fredrikson, M., and Jha, S. Privacy risk in machine learning: Analyzing the connection
to overfitting. CSF 2018.
• [DR’14] Cynthia Dwork, Aaron Roth, et al. The algorithmic foundations of differential privacy. Foundations and
Trends in Theoretical Computer Science, 9(3–4):211–407, 2014.
• [DSZ’16] Anupam Datta, Shayak Sen, and Yair Zick. Algorithmic transparency via quantitative input influence: Theory
and experiments with learning systems. In Security and Privacy (SP), 2016 IEEE Symposium on, pp. 598–617. IEEE,
2016
• [KLRS’17] Matt J Kusner, Joshua Loftus, Chris Russell, and Ricardo Silva. Counterfactual fairness. In Advances in
Neural Information Processing Systems, pp. 4066–4076, 2017.
• [MTS’19] Mahajan, Divyat, Chenhao Tan, and Amit Sharma. "Preserving Causal Constraints in Counterfactual
Explanations for Machine Learning Classifiers." arXiv preprint arXiv:1912.03277 (2019).
• [MTS’20] Mahajan, Divyat, Shruti Tople and Amit Sharma. “Domain Generalization using Causal Matching”. arXiv
preprint arXiv:2006.07500, 2020.
• [NDSS’19] Salem, A., Zhang, Y., Humbert, M., Fritz, M., and Backes, M. Ml-leaks: Model and data independent
membership inference attacks and defenses on machine learning models. NDSS 2019.
• [SP’17] Shokri, R., Stronati, M., Song, C., and Shmatikov, V. Membership inference attacks against machine learning
models. Security and Privacy (SP), 2017.
• [SP’19] Nasr, M., Shokri, R., and Houmansadr, A. Comprehensive privacy analysis of deep learning: Stand-alone and
federated learning under passive and active white-box inference attacks. Security and Privacy (SP), 2019.