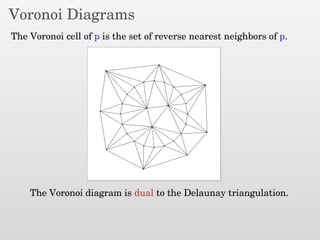
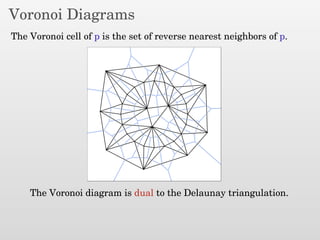
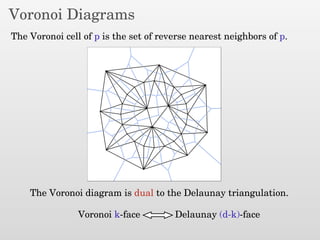
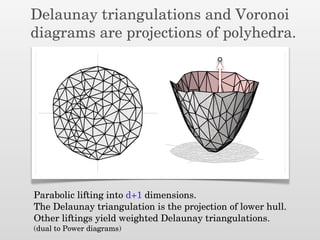
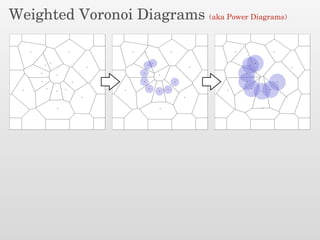
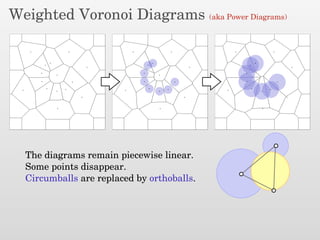
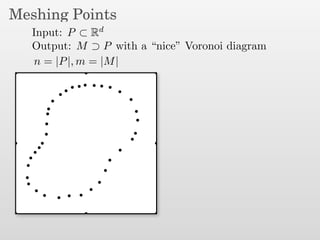
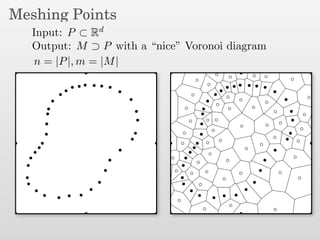
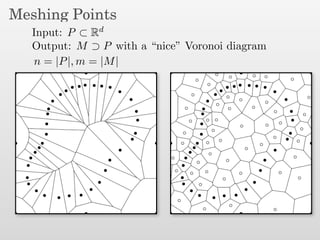
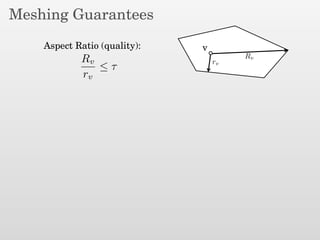
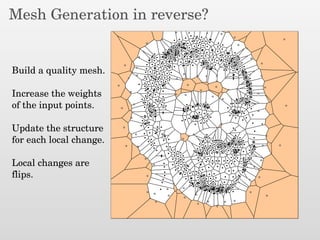
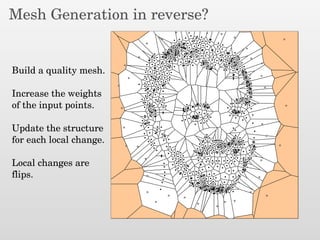
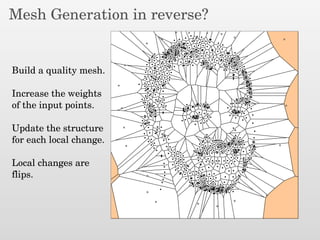
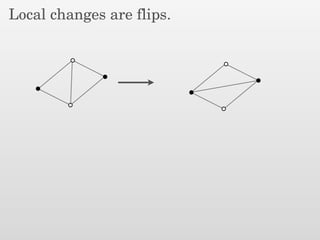
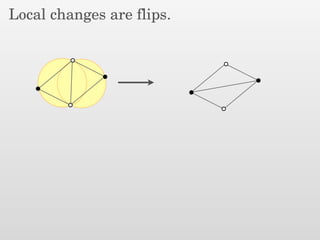
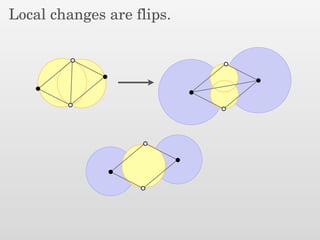
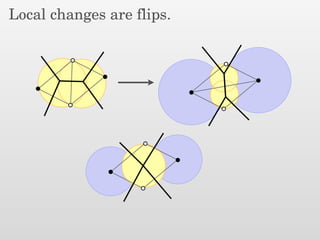
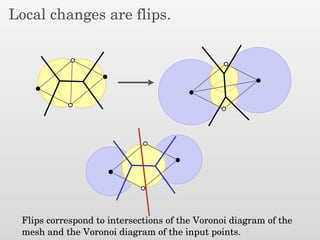
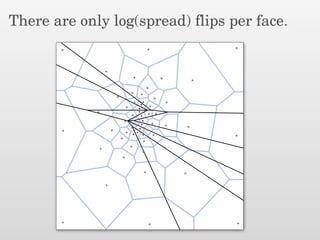
The document presents a new output-sensitive algorithm for constructing Voronoi diagrams and Delaunay triangulations in d-dimensions, emphasizing a method that begins with a quality mesh and subsequently removes Steiner points. It discusses the relationship between Voronoi diagrams and Delaunay triangulations, as well as various techniques employed in the algorithm, including maintaining a bounding box and managing local changes through flips. The algorithm achieves a running time of O(f log n log ∆), leveraging geometric properties to control combinatorial changes.

1. A New Approach to Output-Sensitive
Voronoi Diagrams
and
Delaunay Triangulations
Don Sheehy
INRIA Saclay, France
soon: UConn
Joint work with Gary Miller at CMU

2. Voronoi Diagrams

3. Voronoi Diagrams
The Voronoi cell of p is the set of reverse nearest neighbors of p.

4. Voronoi Diagrams
The Voronoi cell of p is the set of reverse nearest neighbors of p.

5. Voronoi Diagrams
The Voronoi cell of p is the set of reverse nearest neighbors of p.
The Voronoi diagram is dual to the Delaunay triangulation.

6. Voronoi Diagrams
The Voronoi cell of p is the set of reverse nearest neighbors of p.
The Voronoi diagram is dual to the Delaunay triangulation.

7. Voronoi Diagrams
The Voronoi cell of p is the set of reverse nearest neighbors of p.
The Voronoi diagram is dual to the Delaunay triangulation.

8. Voronoi Diagrams
The Voronoi cell of p is the set of reverse nearest neighbors of p.
The Voronoi diagram is dual to the Delaunay triangulation.
Voronoi k-face Delaunay (d-k)-face

9. Voronoi Diagrams and Delaunay
triangulations are used everywhere.

10. Voronoi Diagrams and Delaunay
triangulations are used everywhere.
Geographical Information Systems

11. Voronoi Diagrams and Delaunay
triangulations are used everywhere.
Geographical Information Systems
Graphics

12. Voronoi Diagrams and Delaunay
triangulations are used everywhere.
Geographical Information Systems
Graphics
Topological Data Analysis

13. Voronoi Diagrams and Delaunay
triangulations are used everywhere.
Geographical Information Systems
Graphics
Topological Data Analysis
Mesh Generation

14. Delaunay triangulations and Voronoi
diagrams are projections of polyhedra.

15. Delaunay triangulations and Voronoi
diagrams are projections of polyhedra.
Parabolic lifting into d+1 dimensions.
The Delaunay triangulation is the projection of lower hull.
Other liftings yield weighted Delaunay triangulations.
(dual to Power diagrams)

16. Delaunay triangulations and Voronoi
diagrams are projections of polyhedra.
Parabolic lifting into d+1 dimensions.
The Delaunay triangulation is the projection of lower hull.
Other liftings yield weighted Delaunay triangulations.
(dual to Power diagrams)

17. Weighted Voronoi Diagrams (aka Power Diagrams)

18. Weighted Voronoi Diagrams (aka Power Diagrams)
The diagrams remain piecewise linear.

19. Weighted Voronoi Diagrams (aka Power Diagrams)
The diagrams remain piecewise linear.
Some points disappear.

20. Weighted Voronoi Diagrams (aka Power Diagrams)
The diagrams remain piecewise linear.
Some points disappear.
Circumballs are replaced by orthoballs.

21. Weighted Voronoi Diagrams (aka Power Diagrams)
The diagrams remain piecewise linear.
Some points disappear.
Circumballs are replaced by orthoballs.

22. A brief history of Voronoi Diagram algorithms.
(Convex Hull)

23. A brief history of Voronoi Diagram algorithms.
O(n log n + n d/2
)Chazelle ’93
(Convex Hull)

24. A brief history of Voronoi Diagram algorithms.
O(n log n + n d/2
)Chazelle ’93
(Convex Hull)
Swart ’85
Avis & Fukuda ’92
O(nf)

25. A brief history of Voronoi Diagram algorithms.
O(n log n + n d/2
)Chazelle ’93
(Convex Hull)
Swart ’85
Avis & Fukuda ’92
O(nf)
O(n2
+ f log n)Seidel ’86

26. A brief history of Voronoi Diagram algorithms.
O(n log n + n d/2
)Chazelle ’93
(Convex Hull)
Swart ’85
Avis & Fukuda ’92
O(nf)
O(n2
+ f log n)Seidel ’86
O(n2− 2
d/2 +1 logO(1)
n + f log n)
Matousek and
Schwartzkopf ’92

27. A brief history of Voronoi Diagram algorithms.
O(n log n + n d/2
)Chazelle ’93
(Convex Hull)
Swart ’85
Avis & Fukuda ’92
O(nf)
O(n2
+ f log n)Seidel ’86
O(n2− 2
d/2 +1 logO(1)
n + f log n)
Matousek and
Schwartzkopf ’92
O(n log f + (nf)1− 1
d/2 +1 logO(1)
n)Chan’96

28. A brief history of Voronoi Diagram algorithms.
O(n log n + n d/2
)Chazelle ’93
(Convex Hull)
Swart ’85
Avis & Fukuda ’92
O(nf)
O(n2
+ f log n)Seidel ’86
O(n2− 2
d/2 +1 logO(1)
n + f log n)
Matousek and
Schwartzkopf ’92
O(n log f + (nf)1− 1
d/2 +1 logO(1)
n)Chan’96
O((n + (nf)1− 1
d/2 + fn1− 2
d/2 ) logO(1)
n)
Chan,
Snoeyink,
Yap ’97

29. A brief history of Voronoi Diagram algorithms.
O(n log n + n d/2
)Chazelle ’93
O(f log n log ∆)Miller and Sheehy
(today’s talk)
(Convex Hull)
Swart ’85
Avis & Fukuda ’92
O(nf)
O(n2
+ f log n)Seidel ’86
O(n2− 2
d/2 +1 logO(1)
n + f log n)
Matousek and
Schwartzkopf ’92
O(n log f + (nf)1− 1
d/2 +1 logO(1)
n)Chan’96
O((n + (nf)1− 1
d/2 + fn1− 2
d/2 ) logO(1)
n)
Chan,
Snoeyink,
Yap ’97

30. Meshing Points
Input: P ⊂ Rd
Output: M ⊃ P with a “nice” Voronoi diagram
n = |P|, m = |M|

31. Meshing Points
Input: P ⊂ Rd
Output: M ⊃ P with a “nice” Voronoi diagram
n = |P|, m = |M|

32. Meshing Points
Input: P ⊂ Rd
Output: M ⊃ P with a “nice” Voronoi diagram
n = |P|, m = |M|

33. Meshing Points
Input: P ⊂ Rd
Output: M ⊃ P with a “nice” Voronoi diagram
n = |P|, m = |M|

34. Meshing Points
Input: P ⊂ Rd
Output: M ⊃ P with a “nice” Voronoi diagram
n = |P|, m = |M|
Counterintuitive Fact about Meshing:
It’s sometimes easier to build the Voronoi/Delaunay
of a superset of the input, than of the input alone.

35. Meshing Guarantees

36. Meshing Guarantees
Aspect Ratio (quality): v
Rv
rv
Rv
rv
≤ τ

37. Meshing Guarantees
Aspect Ratio (quality):
Cell Sizing:
v
Rv
rv
Rv
rv
≤ τ
lfs(x) := d(x, P {NN(x)})
1
K
lfs(v) ≤ Rv ≤ Klfs(v)

38. Meshing Guarantees
Aspect Ratio (quality):
Cell Sizing:
Constant Local Complexity:
v
Rv
rv
Rv
rv
≤ τ
lfs(x) := d(x, P {NN(x)})
Each cell has at most a constant number of faces.
1
K
lfs(v) ≤ Rv ≤ Klfs(v)

39. Meshing Guarantees
Aspect Ratio (quality):
Cell Sizing:
Constant Local Complexity:
Optimal Size:
v
Rv
rv
Rv
rv
≤ τ
lfs(x) := d(x, P {NN(x)})
|M| = Θ(|Optimal|)
Each cell has at most a constant number of faces.
1
K
lfs(v) ≤ Rv ≤ Klfs(v)

40. Meshing Guarantees
Aspect Ratio (quality):
Cell Sizing:
Constant Local Complexity:
Optimal Size:
v
Rv
rv
Rv
rv
≤ τ
lfs(x) := d(x, P {NN(x)})
|M| = Θ(|Optimal|)
Running time: O(n log n + |M|)
Each cell has at most a constant number of faces.
1
K
lfs(v) ≤ Rv ≤ Klfs(v)

41. Mesh Generation in reverse?

42. Mesh Generation in reverse?
Build a quality mesh.

43. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.

44. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.

45. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

46. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

47. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

48. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

49. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

50. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

51. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

52. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

53. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

54. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

55. Mesh Generation in reverse?
Build a quality mesh.
Increase the weights
of the input points.
Update the structure
for each local change.
Local changes are
flips.

56. The Algorithm

57. The Algorithm
Add a bounding box around the points.

58. The Algorithm
Add a bounding box around the points.
Build a quality mesh of the points.

59. The Algorithm
Add a bounding box around the points.
Build a quality mesh of the points.
Keep potential flips on a heap ordered by flip time.

60. The Algorithm
Add a bounding box around the points.
Build a quality mesh of the points.
Keep potential flips on a heap ordered by flip time.
(flip time is the weight of the input points when the flip happens)

61. The Algorithm
Add a bounding box around the points.
Build a quality mesh of the points.
Keep potential flips on a heap ordered by flip time.
(flip time is the weight of the input points when the flip happens)
Repeatedly pop a flip, attempt to do it, and update.

62. The Algorithm
Add a bounding box around the points.
Build a quality mesh of the points.
Keep potential flips on a heap ordered by flip time.
(flip time is the weight of the input points when the flip happens)
Repeatedly pop a flip, attempt to do it, and update.
(at most O(1) new potential flips are added to the heap)

63. The Algorithm
Add a bounding box around the points.
Build a quality mesh of the points.
Keep potential flips on a heap ordered by flip time.
(flip time is the weight of the input points when the flip happens)
Repeatedly pop a flip, attempt to do it, and update.
(at most O(1) new potential flips are added to the heap)
When the heap is empty, remove the bounding box and
all incident Delaunay faces.

64. Local changes are flips.

65. Local changes are flips.

66. Local changes are flips.

67. Local changes are flips.

68. Local changes are flips.

69. Local changes are flips.

70. Local changes are flips.

71. Local changes are flips.
Flips correspond to intersections of the Voronoi diagram of the
mesh and the Voronoi diagram of the input points.

72. There are only log(spread) flips per face.

73. There are only log(spread) flips per face.

74. There are only log(spread) flips per face.

75. A summary of the analysis.

76. A summary of the analysis.
Full dimensional mesh cells intersect output faces at
most log(spread) times.

77. A summary of the analysis.
Full dimensional mesh cells intersect output faces at
most log(spread) times.
Since each mesh cell has only a constant number of
faces, we only get O(f log(spread)) total flips.

78. A summary of the analysis.
Full dimensional mesh cells intersect output faces at
most log(spread) times.
Since each mesh cell has only a constant number of
faces, we only get O(f log(spread)) total flips.
Each flip generates at most O(1) new flips on the heap.

79. A summary of the analysis.
Full dimensional mesh cells intersect output faces at
most log(spread) times.
Since each mesh cell has only a constant number of
faces, we only get O(f log(spread)) total flips.
Each flip generates at most O(1) new flips on the heap.
The heap operations require O(log n) time each.

80. A summary of the analysis.
Full dimensional mesh cells intersect output faces at
most log(spread) times.
Since each mesh cell has only a constant number of
faces, we only get O(f log(spread)) total flips.
Each flip generates at most O(1) new flips on the heap.
The heap operations require O(log n) time each.
Total running time is O(f log n log (spread)).

81. Summary

82. Summary
A new output-sensitive algorithm for Voronoi diagrams and
Delaunay triangulations in d-dimensions.

83. Summary
A new output-sensitive algorithm for Voronoi diagrams and
Delaunay triangulations in d-dimensions.
Start with a quality mesh and then remove the Steiner points.

84. Summary
A new output-sensitive algorithm for Voronoi diagrams and
Delaunay triangulations in d-dimensions.
Start with a quality mesh and then remove the Steiner points.
Use geometry to bound the combinatorial changes.

85. Summary
A new output-sensitive algorithm for Voronoi diagrams and
Delaunay triangulations in d-dimensions.
Start with a quality mesh and then remove the Steiner points.
Use geometry to bound the combinatorial changes.
O(f log n log ∆)Running time:

86. Summary
A new output-sensitive algorithm for Voronoi diagrams and
Delaunay triangulations in d-dimensions.
Start with a quality mesh and then remove the Steiner points.
Use geometry to bound the combinatorial changes.
O(f log n log ∆)Running time:
Thank you.