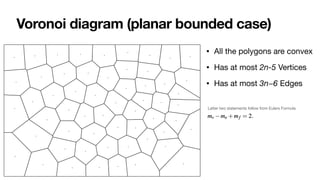
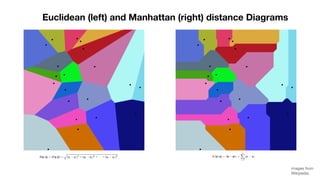
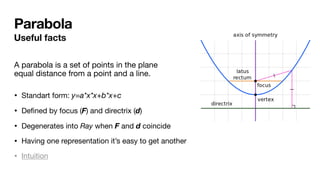
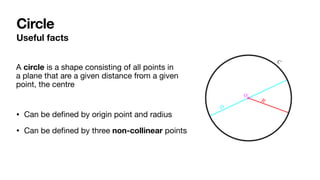
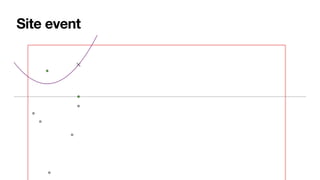
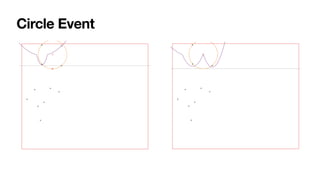
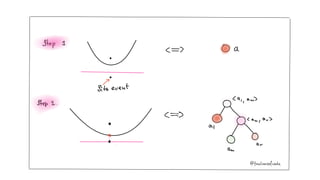
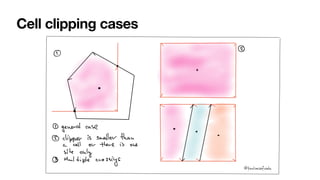
The document summarizes Fortune's algorithm for generating Voronoi diagrams. It begins with background on Voronoi diagrams and their applications. It then outlines Fortune's algorithm, which uses a sweep line and priority queue of events to incrementally build the Voronoi diagram. Key aspects include maintaining a beach line of parabolic arcs, handling site events by splitting arcs and circle events by removing arcs. The algorithm runs in O(n log n) time by using a self-balancing binary search tree to represent the beach line.

1. Oleksandr Glagoliev @fewlinesofcode
Fortune’s algorithm for Voronoi
diagrams
Implementation details

2. Agenda
• What is Voronoi diagram?
• Fortunes algorithm (O(n log(n))
• Brief recall of Math used in the algorithm
• The idea
• Data structures
• Degenerate cases
• Applications and generalization

3. What

4. Voronoi in real life
Oak leaf pattern
Giraffe skin pattern
Tortoise skin and shell patterns
Soap foam pattern

5. Georgy Voronoy
Georgy Voronoy was a Ukrainian
mathematician best known for the
Voronoi diagram which is a
partitioning of a plane into regions
based on distance to a finite set of
points.
Born
28 April 1868
Zhuravka
Died
20 November 1908
Warsaw, Poland

6. Voronoi Diagram is a diagram that assigns a set of predefined points
in a plane into an equal number of cells, such that each point p is
inside a cell consisting of all regions closer to p than to any other
point.
Originally, these diagrams have been defined for a given set of points, called
sites in Euclidean space, and for the Euclidean distance.

7. Voronoi diagram (planar bounded case)
• All the polygons are convex
• Has at most 2n-5 Vertices
• Has at most 3n−6 Edges
Latter two statements follow from Eulers Formula

8. Interactive samples

9. Visualizing Voronoi generation
through expanding circles
Images by jakericedesigns.com and WikiCommons

10. Euclidean (left) and Manhattan (right) distance Diagrams
images from
Wikipedia

11. How

12. Input
Set of Sites Doubly Connected
Edges List
Output
❓→ →Clipping Rectangle?

13. Algorithm Input

14. Site
satellite: AnyData?
x: Numeric
y: Numeric
// Hashed by `x` and `y`
Site: Hashable
Rectangle
x: Numeric
y: Numeric
width: Numeric
height: Numeric
// NB! Helpers and convenience methods are omitted

15. Algorithm Output

16. DCEL image

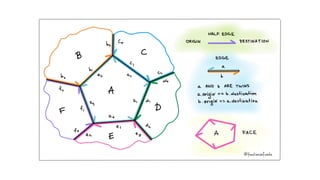
17. Diagram (DCEL)
DCEL
vertices: [Vertex]
halfEdges: [HalfEdge]
faces: [Face]
Vertex
x, y: Numeric
incidentHalfEdge: HalfEdge
HalfEdge
incidentFace: Face
twin: HalfEdge?
origin: Vertex?
destination: Vertex?
// Doubly linked list
prev: HalfEdge
next: HalfEdge
getDestination() -> HalfEdge
return next.origin
getOrigin() -> HalfEdge
return prev.destinationFace
// Doubly linked list of half-edges
incidentHalfEdge: HalfEdge

18. Naive implementation

19. Voronoi diagram algorithm
The naive way
Input: Set of Sites
Output: DCEL containing Voronoi diagram
Init:
- Save reference to the Set of Sites
- If bounding is required, save a reference to a Bounding Rectangle
- Create empty Bisectors list (list of data structures holding the reference to Bisector and two neighbour Sites)
Process:
for each Site in a Set:
- Find the Site closest to current Site excluding ones that are already in the Bisectors list
- Add a record in Bisectors list
for each Bisector in Bisectors list:
Find intersections with other bisectors related to the same Site.
Create Vertex for each intersection.
Create appropriate HalfEdge records.
Terminate:
if bounding required:
- Find points where HalfEdges intersect BoundingRectangle
- Clip edges on intersection points
- Complete cells by filling the gaps with half edges repeating BoundingRectangle's edges
Return resulting Diagram

20. Fortune’s Algorithm

21. Steven Fortune
Technical Manager of the Algorithms Research group within the
Computing Systems Principles department of Bell Laboratories,
Alcatel-Lucent
Source: http://plan9.bell-labs.co/who/sjf/

22. The counterparts
(Bounding omitted)
• Diagram - output structure. Represented by DCEL
• Sweep line - horizontal line moving from top to bottom
• Beachline - status structure keeping the state of the diagram building process. Represented by X-
monotone curve consisting of Arcs
• Arc - Beachline building unit. Represented by parabola with some additional data
• Breakpoint - intersection point of two Arcs
• Site event - happens when site Sweep line shares y with the Site. New cell is added to the Diagram
• Circle event - happens when Arc is removed from the Beachline. New Vertex is added to the Diagram
• Event queue - stores events in correct order. Represented by Priority Queue

23. Intuition
Xcode sample

24. A bit of a Math 🧐

25. Parabola
Useful facts
• Standart form: y=a*x*x+b*x+c
• Defined by focus (F) and directrix (d)
• Degenerates into Ray when F and d coincide
• Having one representation it’s easy to get another
• Intuition
A parabola is a set of points in the plane
equal distance from a point and a line.

26. Circle
Useful facts
• Can be defined by origin point and radius
• Can be defined by three non-collinear points
A circle is a shape consisting of all points in
a plane that are a given distance from a given
point, the centre

27. Curve orientation https://en.wikipedia.org/wiki/Curve_orientation
In two dimensions, given an ordered set of three or more connected
vertices which forms a simple polygon, the orientation of the resulting
polygon is directly related to the cross product (computed as a
determinant of an orientation matrix O) at any vertex of the convex
hull of the polygon.
Orientation matrix Determinant
If the determinant is negative, then the polygon is oriented clockwise. If the determinant
is positive, the polygon is oriented counterclockwise. The determinant is non-zero if
points A, B, and C are non-collinear. In the above example, with points ordered A, B, C,
etc., the determinant is negative, and therefore the polygon is clockwise.

28. Site event

29. Circle Event

30. Fortunes Algorithm
Input: Set of Sites
Output: DCEL containing Voronoi diagram
Init:
- Fill EventQueue with Site events received as an input
- If bounding is required, save a reference to a Bounding Rectangle
Process:
While the Event Queue is not empty:
Pop the top event
if the event is a SiteEvent
HANDLE_SITE_EVENT(se)
else
// Event is a CircleEvent
HANDLE_CIRCLE_EVENT(ce)
Terminate:
if bounding required:
- Find points where HalfEdges intersect BoundingRectangle
- Clip edges on intersection points
- Complete cells by filling the gaps with half edges repeating BoundingRectangle's eddges
Return result

31. Site event handling
Classic implementation
T: Self-balancing Binary Search Tree holding Beachline
SE: Site event
EQ: Event queue
1. If T is empty, insert SE into it (so that T consists of a single leaf storing SE) and return. Otherwise, continue with steps 2-5.
2. Search in T for the arc A vertically above SE.
If the leaf representing A has a pointer to a circle event in EQ, then this circle event is a false alarm and it must be deleted from EQ.
3. Replace the leaf of T that represents an Arc with a subtree having three leaves.
The middle leaf stores the new site pi and the other two leaves store the site pj that was originally stored with an Arc.
Store the tuples <pj, pi> and <pi, pj> representing the new breakpoints at the two new internal nodes.
Perform rebalancing operations on T if necessary (!!!)
4. Create new HalfEdge records in the Diagram structure for the edge separating V(pi) and V(pj),
which will be traced out by the two new breakpoints.
5. Check the triple of consecutive arcs where the new arc for SE is the left arc to see if the breakpoints converge(!!!).
If so, insert the circle event into EQ and add pointers between the node in T and the node in Q.
Do the same for the triple where the new arc is the right arc.

32. Circle Event Handling
Classic implementation
1. Delete the leaf that represents the disappearing arc from T.
Update the tuples representing the breakpoints at the internal nodes. (!!!)
Perform rebalancing operations on T if necessary (!!!).
Delete all circle events involving disappearing arc from EQ;
These can be found using the pointers from the predecessor and the successor of disappearing arc in T.
(The circle event where disappearing arc is the middle arc is currently being handled, and has already been deleted from EQ.)
2. Add the center of the circle causing the event as a Vertex record to the doubly-connected edge list storing the Voronoi diagram under construction.
Create two HalfEdge records corresponding to the new breakpoint of the Beachline.
Set the pointers between them appropriately.
Attach the three new records to the HalfEdge records that end at the Vertex.
3. Check the new triple of consecutive arcs that has the former left neighbor of disappearing arc as
its middle arc to see if the two breakpoints of the triple converge.
If so, insert the corresponding circle event into EQ and set pointers between the new circle event in EQ and the corresponding leaf of T.
Do the same for the triple where the former right neighbor is the middle arc.

34. Show extreme balancing case

35. “Perform tree rebalancing operations if needed”

36. Problems with classic implementation
• Beachline data structure requires two types of nodes (Tuple node and Arc
node)
• Tree balancing is hard and there is little to no information on how to do it
• No tree-balancing - no O(n*log(n))

37. Modified Fortune’s algorithm

38. Data structures

39. Event data structure
/// Event
Event
kind: EventKind // SITE | CIRCLE
point: Site
arc: Arc?
circle: Circle?
Event: Equatable, Comparable
// Equatable
== // Events are equal if their `kind` and `point` are equal
// Comparable
< // Events are compared using `point.y`. If both event points share the same `y` we compare `point.x`

40. Red-black tree
A red-black tree is a binary tree that satisfies the following red-black
properties:
1. Every node is either red or black.
2. The root is black.
3. Every leaf (nil) is black.
4. If a node is red, then both its children are black.
5. For each node, all simple paths from the node to descendant leaves
contain the same number of black nodes.

41. Red-black tree example

42. Beachline
Beachline
sweeplineY: Numeric = 0
root: Arc?
// Taken from CRLS Red-black tree
minimum(x: Arc) -> Arc
maximum(x: Arc) -> Arc
delete(z: Arc)
insertFixup(z: Arc)
deleteFixup(x: Arc)
rightRotate(x: Arc)
leftRotate(x: Arc)
transplant(u: Arc, v: Arc)
// Algorithm specific
insertRootArc(point: Site) -> Arc
addAsLeftChild(x: Arc, y: Arc)
addAsRightChild(x: Arc, y: Arc)
// Bool variable stands for `is it an edge case`
insertArcForPoint(p: Site) -> (Arc, Bool) // replaces Red-black tree search
handleSpecialArcInsertionCase(p: Site) -> Arc // Added for one specific case
insertSuccessor(p: Arc, s: Arc)

43. Arc
Arc
point: Site?
event: Event?
// Linked list
prev: Arc?
next: Arc?
// Diagram
leftHalfEdge: HalfEdge?
rightHalfEdge: HalfEdge?
cell: Cell!
// Red-black tree
isBlack: Bool // true by default
right: Arc?
left: Arc?
parent: Arc?
// Returns `x` coordinate of left and right Arc bounds (points where arc intersects another Arcs (l and r))
// - infinity to + infinity by default
bounds(directrixY: Numeric) -> (left: Numeric, right: Numeric)

44. Differences in event handling

45. Site event handling
T: Self-balancing Binary Search Tree holding Beachline
SE: Site event
EQ: Event queue
1. If T is empty, insert SE into it (so that T consists of a single leaf storing SE) and return. Otherwise, continue with steps 2-5.
2. Search in T for the arc A vertically above SE.
If the leaf representing A has a pointer to a circle event in EQ, then this circle event is a false alarm and it must be deleted from EQ.
3. Replace the leaf of T that represents an Arc with a subtree having three leaves.
The middle leaf stores the new site pi and the other two leaves store the site pj that was originally stored with an Arc.
Store the tuples <pj, pi> and <pi, pj> representing the new breakpoints at the two new internal nodes.
Perform rebalancing operations on T if necessary (!!!)
3. Create a copy of the Arc vertically above point. Create a new node in T that represent new Arc. Add new node as a left or right child of
an Arc above (depending on the site X). Handle degenerate cases. Add copy of an old arc as a successor of a new arc. Maintain linked list betwee
Perform tree balancing operations by running `insertFixup`.
4. Create new HalfEdge records in the Diagram structure for the edge separating V(pi) and V(pj),
which will be traced out by the two new breakpoints.
4. Create two new HalfEdge records and maintain proper pointers between them. Create new Cell record in the Diagram structure.
5. Check the triple of consecutive arcs where the new arc for SE is the left arc to see if the breakpoints converge(!!!).
If so, insert the circle event into EQ and add pointers between the node in T and the node in Q.
Do the same for the triple where the new arc is the right arc.

46. Circle Event Handling
1. Delete the leaf that represents the disappearing arc from T.
Update the tuples representing the breakpoints at the internal nodes. (!!!)
Perform rebalancing operations on T if necessary (!!!).
Delete all circle events involving disappearing arc from EQ;
These can be found using the pointers from the predecessor and the successor of disappearing arc in T.
(The circle event where disappearing arc is the middle arc is currently being handled, and has already been deleted from EQ.)
1. Delete the leaf that represents the disappearing arc from T. Maintain linked list in the Beachline. Perform tree rebalancing using `deleteFixup`
Delete all circle events involving disappearing arc from EQ;
2. Add the center of the circle causing the event as a Vertex record to the doubly-connected edge list storing the Voronoi diagram under construction.
Create two HalfEdge records corresponding to the new breakpoint of the Beachline.
Set the pointers between them appropriately.
Attach the three new records to the HalfEdge records that end at the Vertex.
3. Check the new triple of consecutive arcs that has the former left neighbor of disappearing arc as
its middle arc to see if the two breakpoints of the triple converge.
If so, insert the corresponding circle event into EQ and set pointers between the new circle event in EQ and the corresponding leaf of T.
Do the same for the triple where the former right neighbor is the middle arc.

47. Degenerate cases

48. Problem #1
First two sites in a diagram share same y. Parabolas are
degenerated into parallel rays and so we have no intersection point.
Pick and arbitrary number large enough (either positive or negative,
depending on axis orientation choise) to be safe for our diagram and use it as
y coordinate of the intersection. The x coordinate will lie exactly in the middle
of two focuses.
Solution

49. Problem #2
New breakpoint lies exactly below the other breakpoint.
In this case we do not delete any Arc from the beachline. We will insert new
Arc into the beachline exactly between two existing and maintain linked list
and Binary tree accordingly. Half edges shape will look like three ray star
where one ray is pointing up and angle between rays are even.
Solution
Show Kyiv pavement case

50. Problem #3
“Correct” circle event produces non x-monotonous
Beachline.
Check if circle event points converge by checking curve
orientation. Ignore circle events for non-converging curves.
Solution
Whiteboard?

51. Problem #4
Circle event when circle goes over 4 points, not 3. This
produces one extra zero-length half edge
Ignore it or remove on post-processing if needed. It
doesn’t break the Diagram
Solution

52. Diagram clipping (Optional step)

53. Cell clipping cases

54. Liang-Barsky function
https://www.cs.helsinki.fi/group/goa/viewing/leikkaus/intro.html
http://www.skytopia.com/project/articles/compsci/clipping.html
// Axis-parallel rectangle
Clipper
left: Numeric // Leftmost `x`
right: Numeric // Rightmost `x`
top: Numeric // Min `y`
bottom: Numeric // Max `y`
LiangBarskyResult = (isOriginClipped: Bool, isDestinationClipped: Bool, resultSegment: LineSegment?)
func lb_clip(line: LineSegment, clipper: Clipper) -> LiangBarskyResult

55. Voronoi Clipping
for each Cell in Cells that are still not removed from the Beachline:
Find points where HalfEdges intersect ClipperRectangle.
Depending on the clipping case, combine clipped HalfEdges into pairs that will later be connected.
for each pair in clipped pairs:
create appropriate HalfEdge chain that follows clipper rectangle.
If cell contains Clipper rectangle point:
Add Vertex to the Diagram accordingly.
Free used resources.
Return resulting Diagram.
End.

56. Voronoi Diagram Applications

57. Everywhere 🙂
• https://en.wikipedia.org/wiki/Voronoi_diagram
• Camille Wormser. Generalized Voronoi Diagrams and Applications.
Computer Science [cs]. Université Nice Sophia Antipolis, 2008. English.
tel-00410850

58. Published in 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) 2015
Mathematical models of tumor growth using Voronoi tessellations in pathology slides of kidney cancer

59. Conclusions
• If it works - further investigation needed
• If you don’t know something - you don’t know it (K.O)
• Build a lot of scaffolding. And then a bit more
• Programming is fun as a hobby

60. What to read next
•Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. 2009. Introduction
to Algorithms, Third Edition (3rd. ed.). The MIT Press.
•Mark de Berg, Otfried Cheong, Marc van Kreveld, and Mark Overmars. 2008. Computational
Geometry: Algorithms and Applications (3rd ed. ed.). Springer-Verlag TELOS, Santa Clara, CA,
USA.
•jacquesheunis.com - Voronoi, the intuitive explanation
•Play with `Delaunator` class on observable.hq

61. https://github.com/fewlinesofcode/FortunesAlgorithm

62. Thank you!
follow @fewlinesofcode on Twitter
It’s ok not to 🙂