Don Sheehy, profile picture
Uploaded byDon Sheehy
302 views

New Bounds on the Size of Optimal Meshes

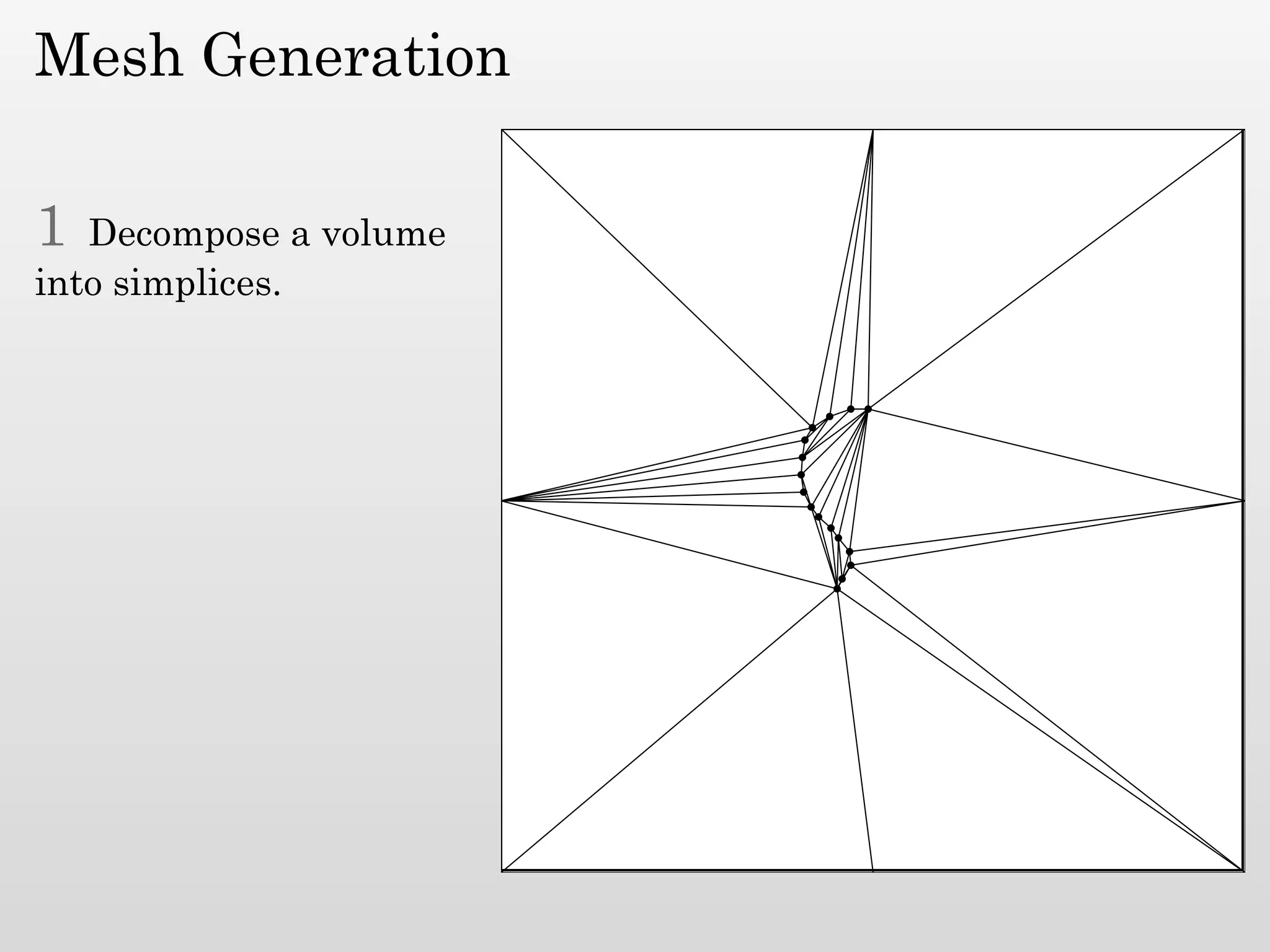
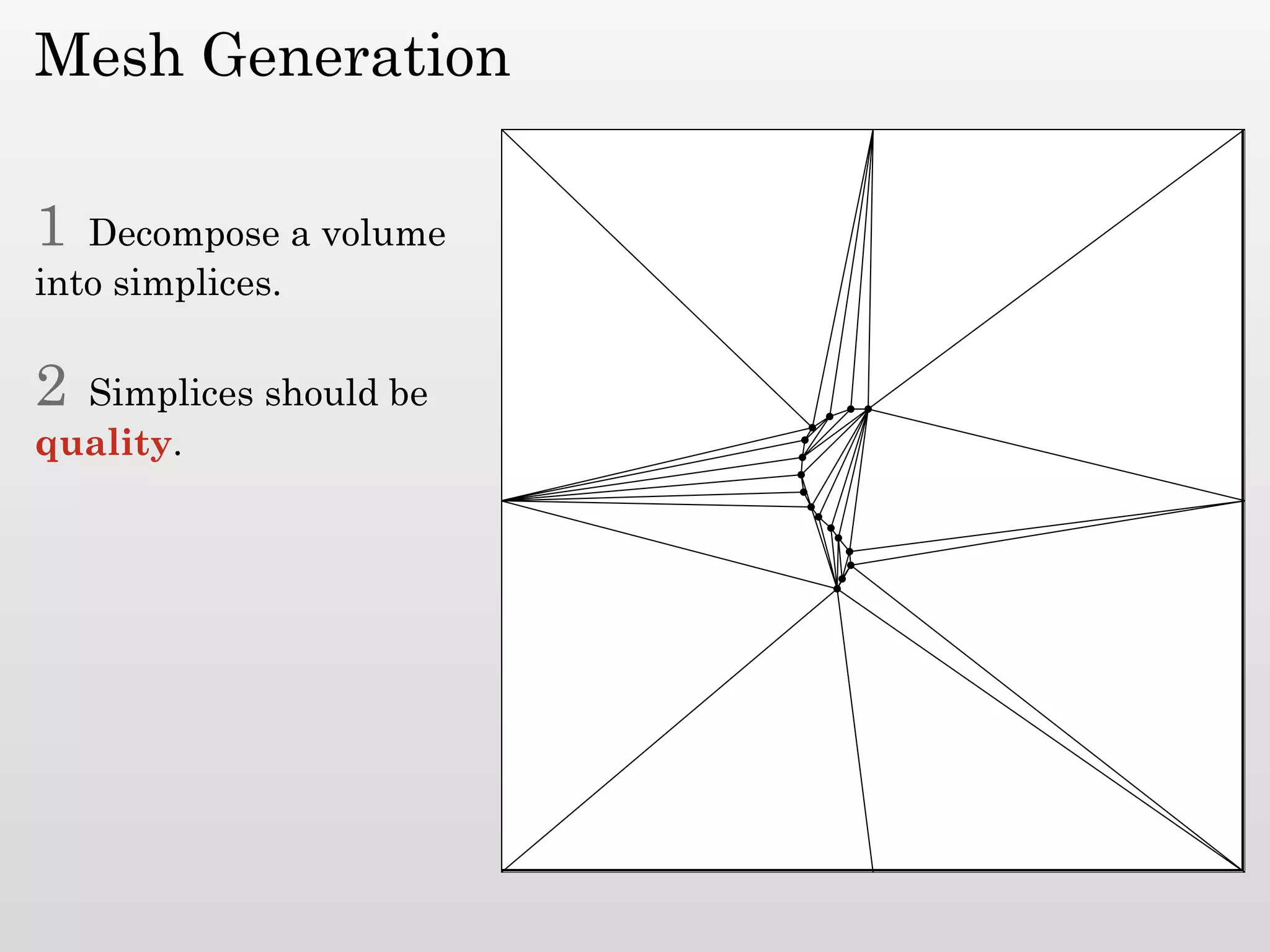
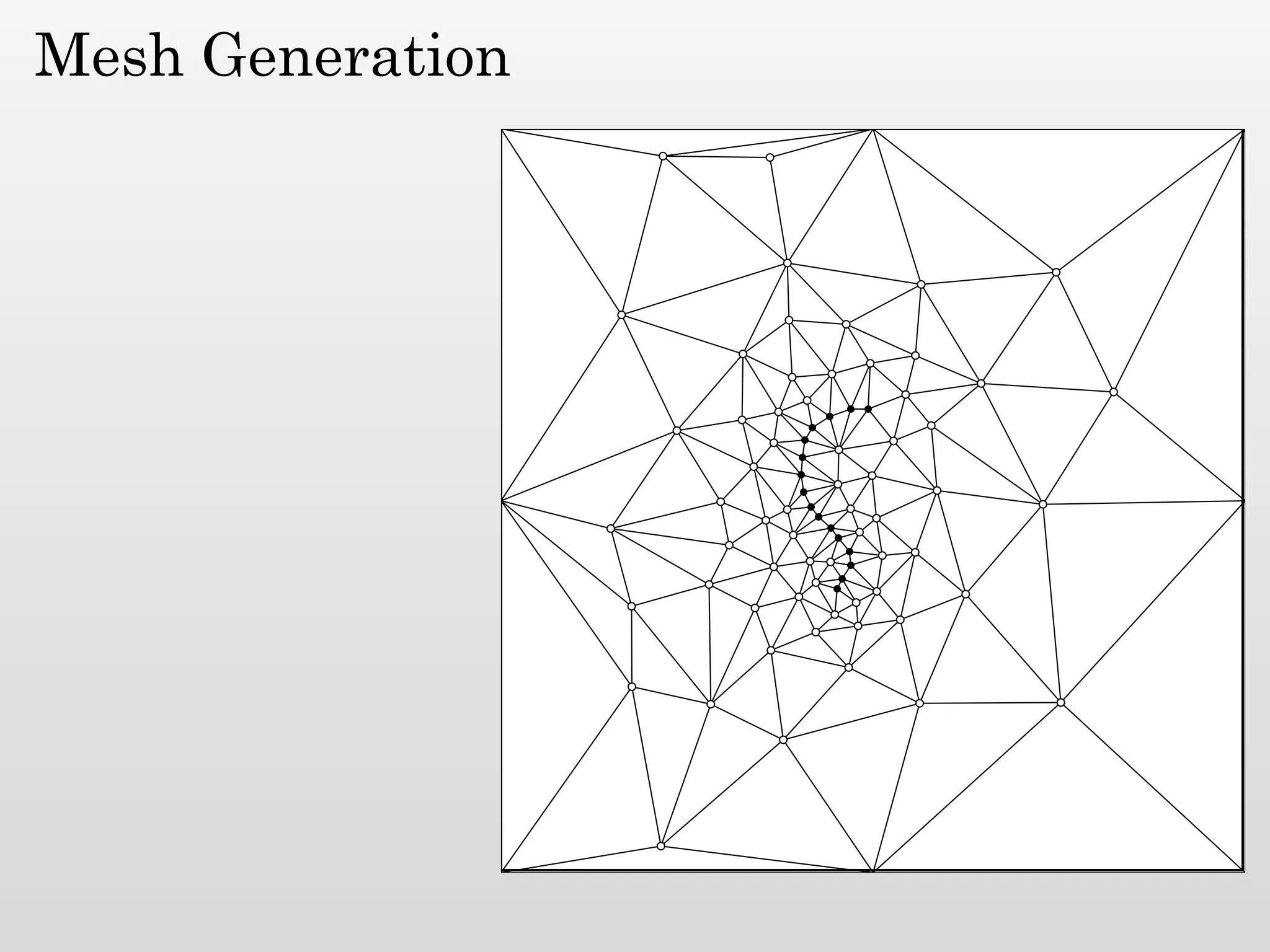
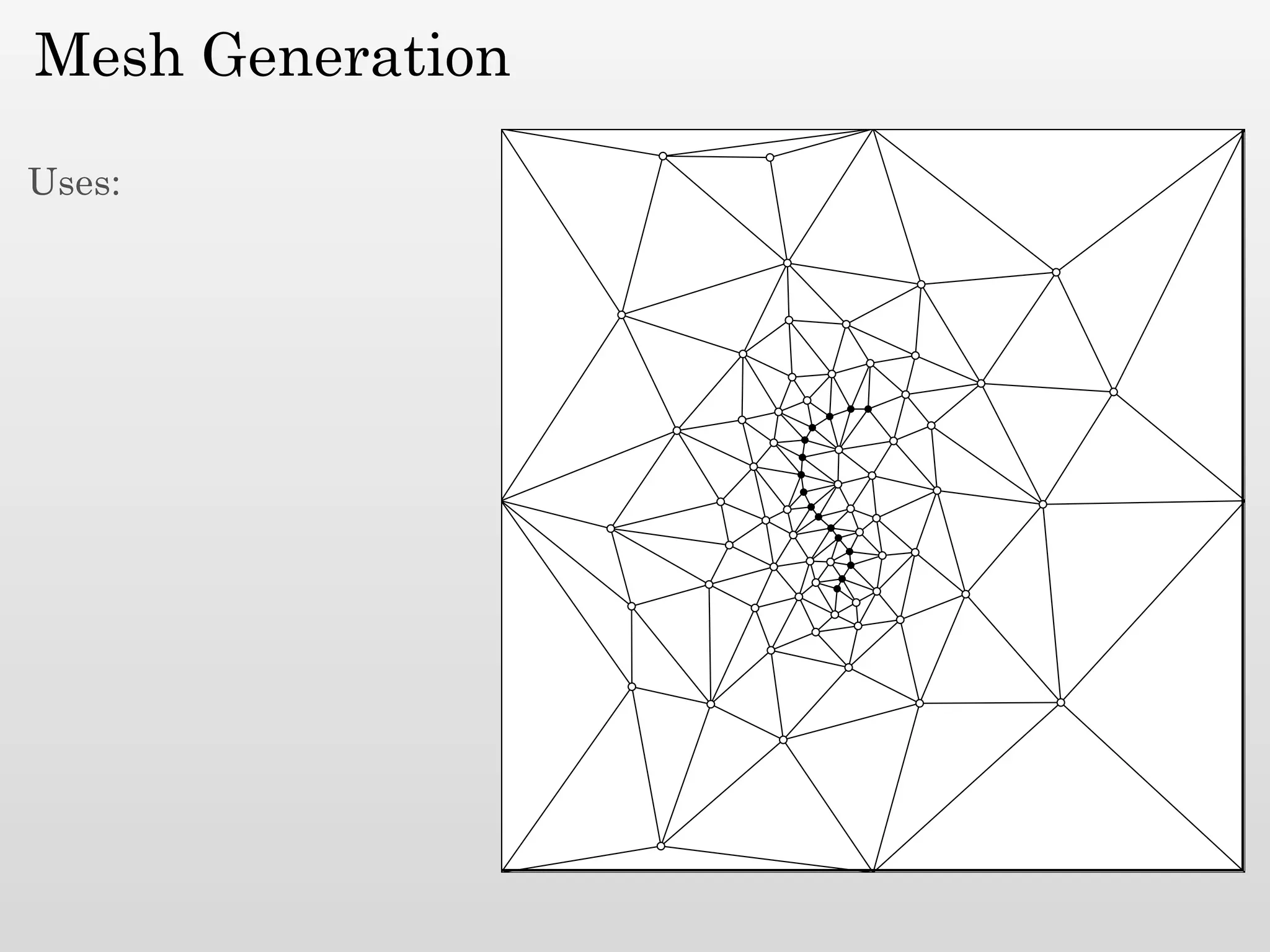
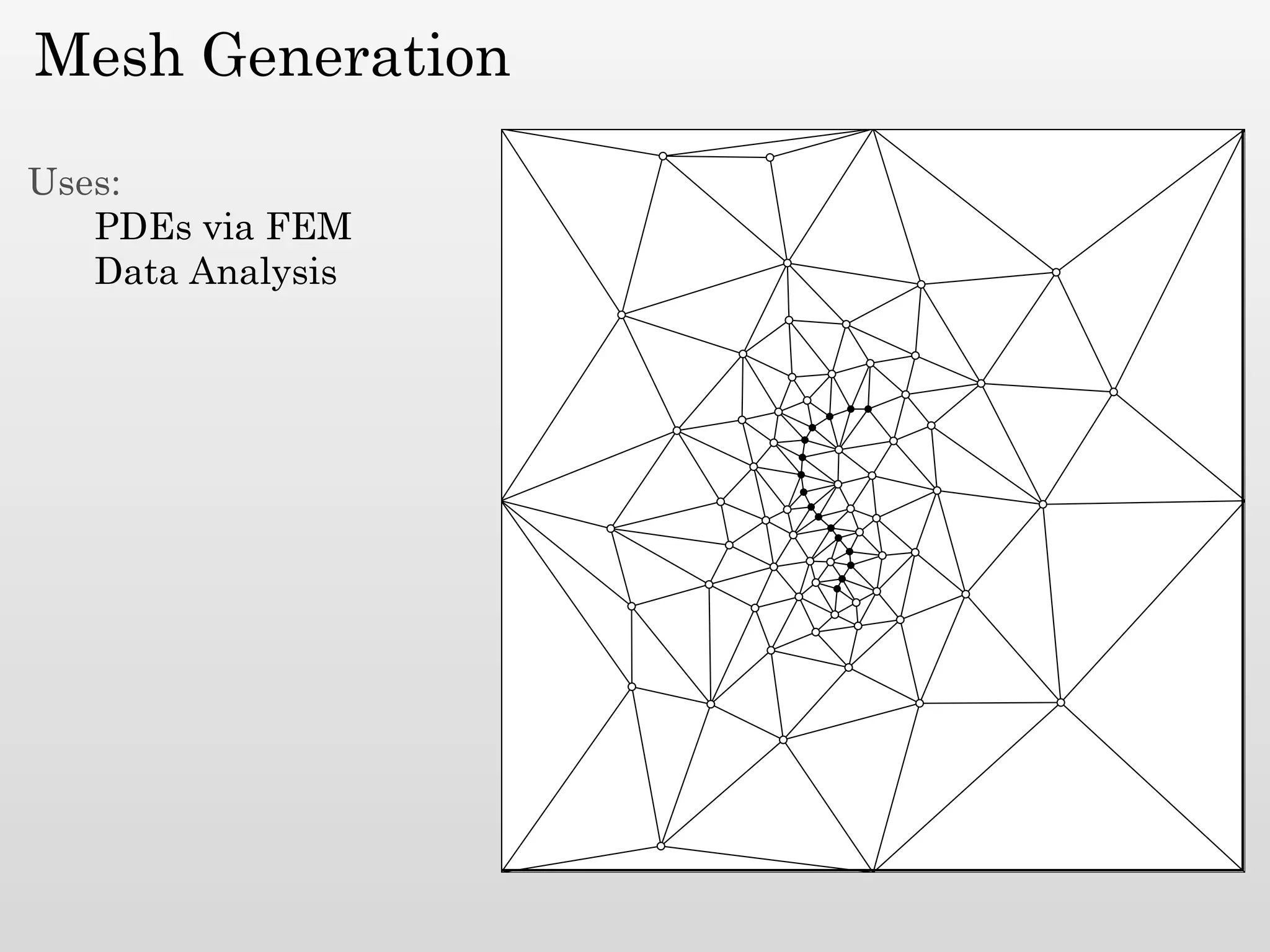
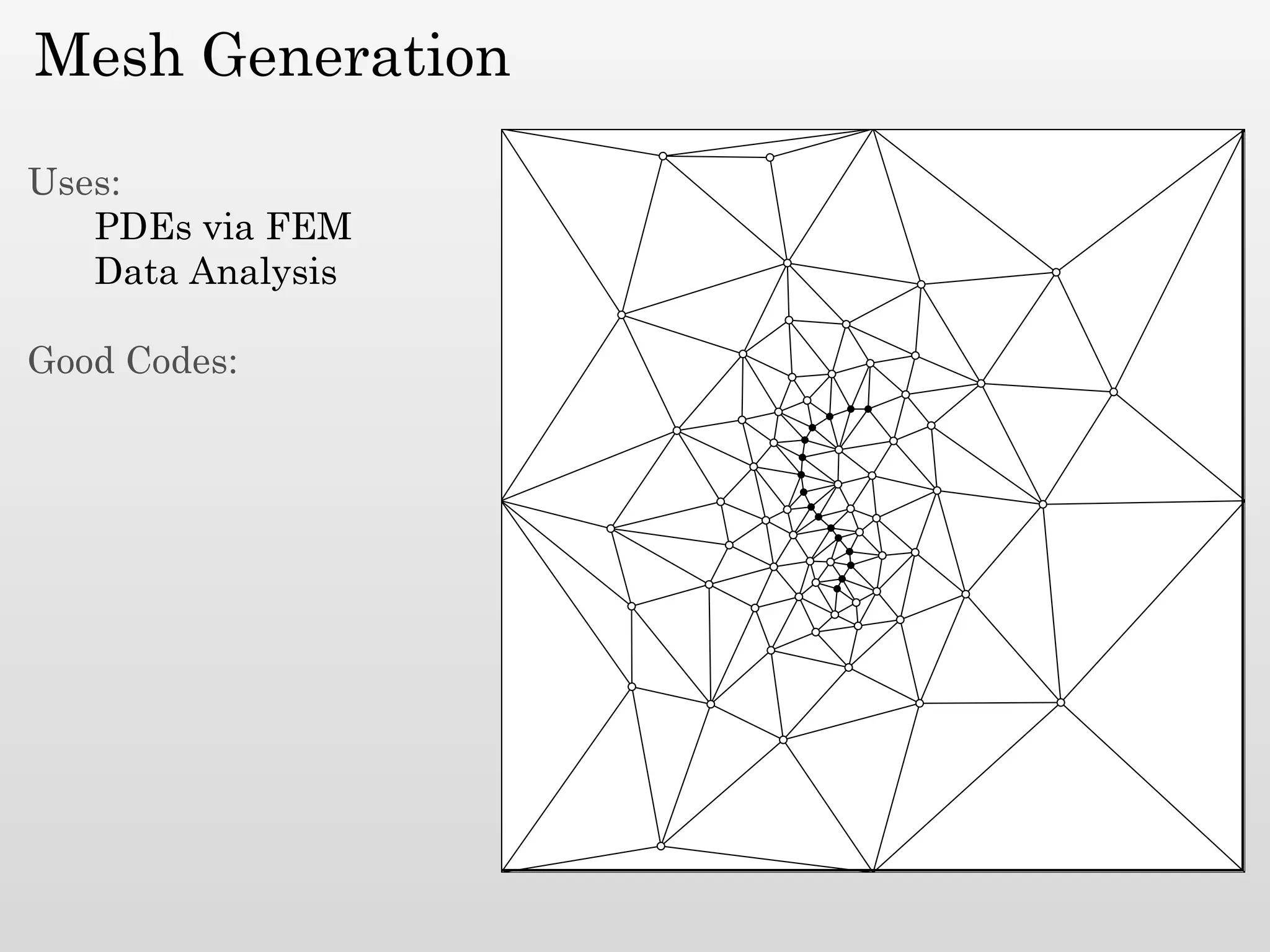
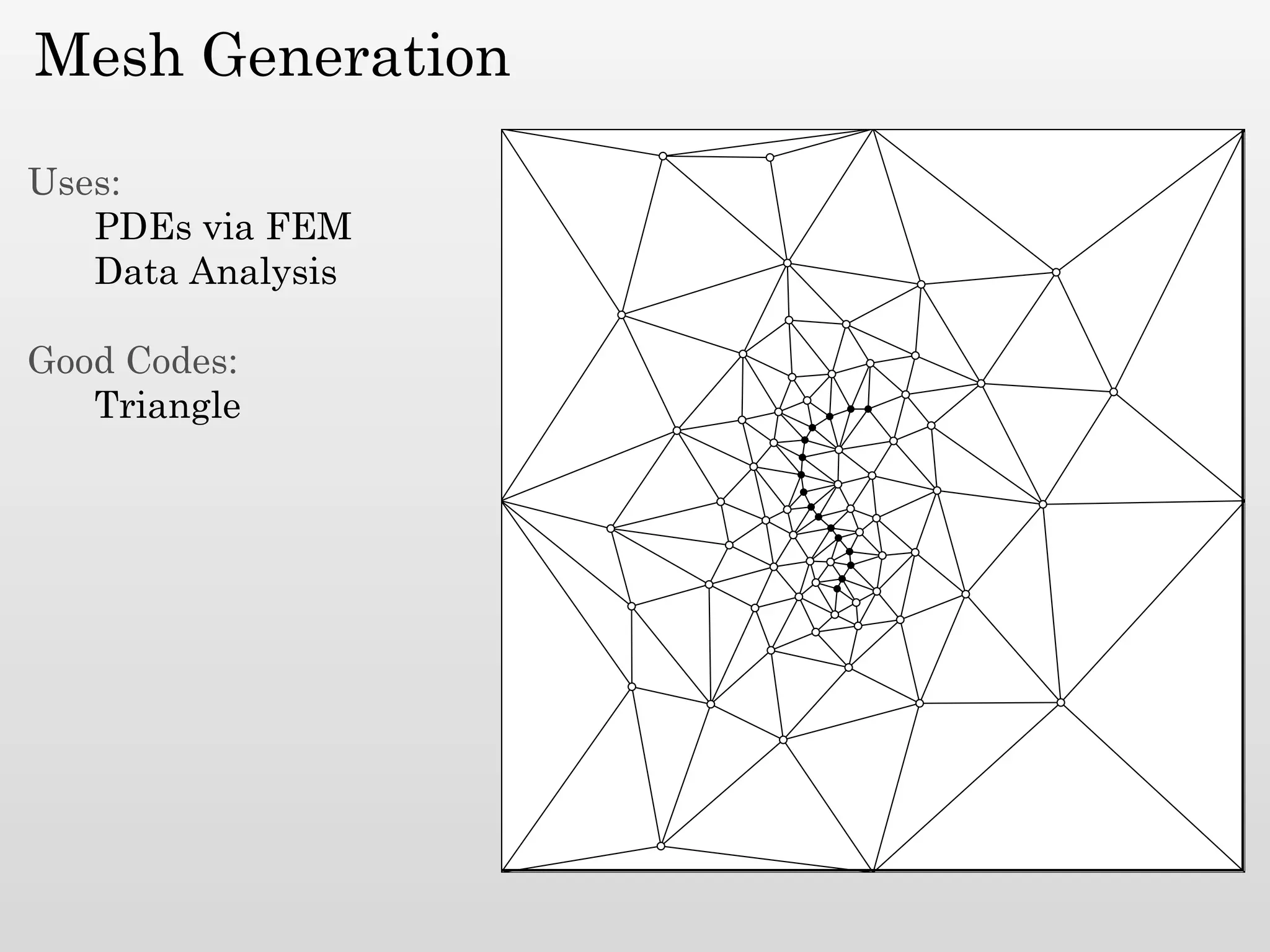
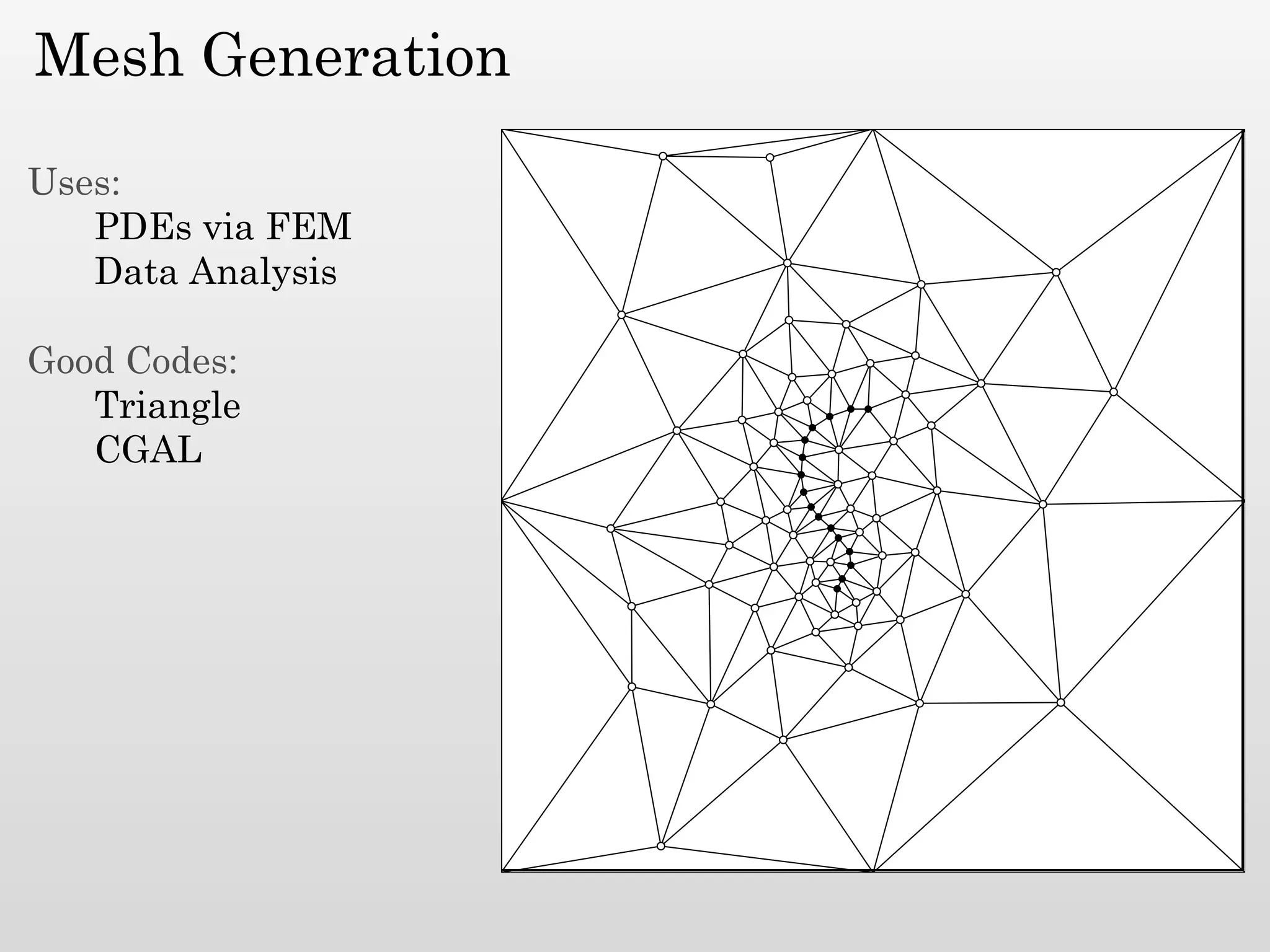
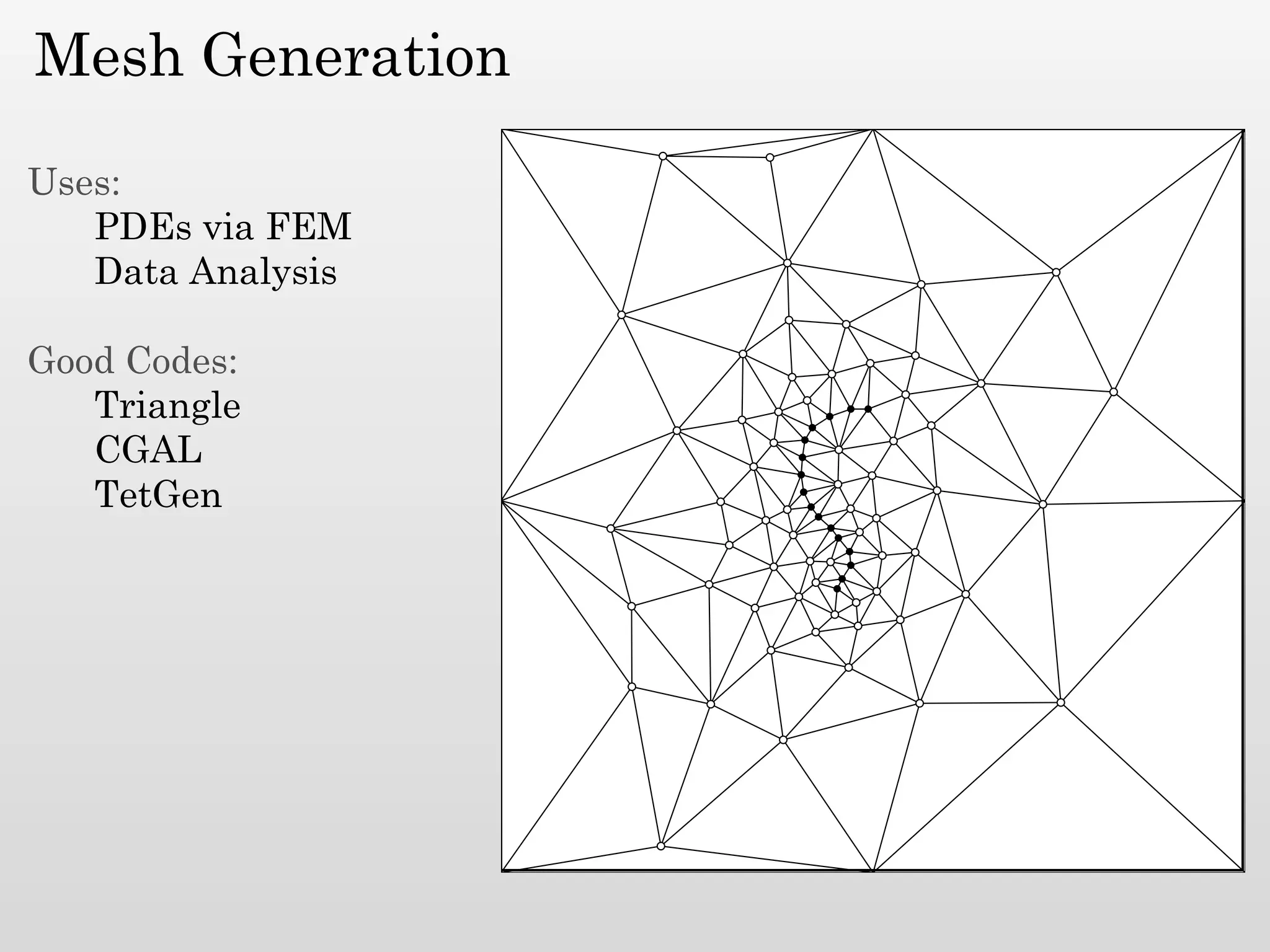
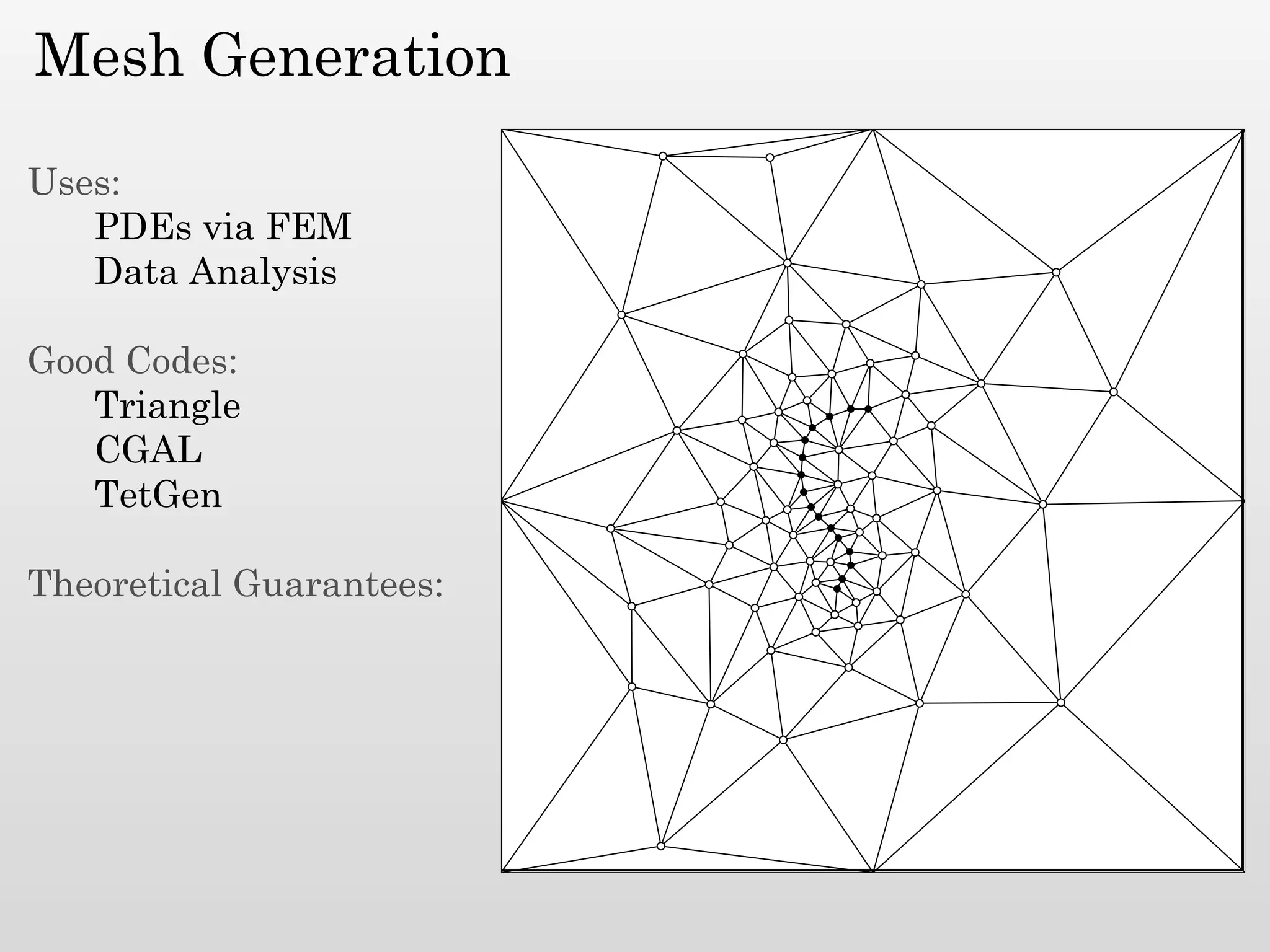
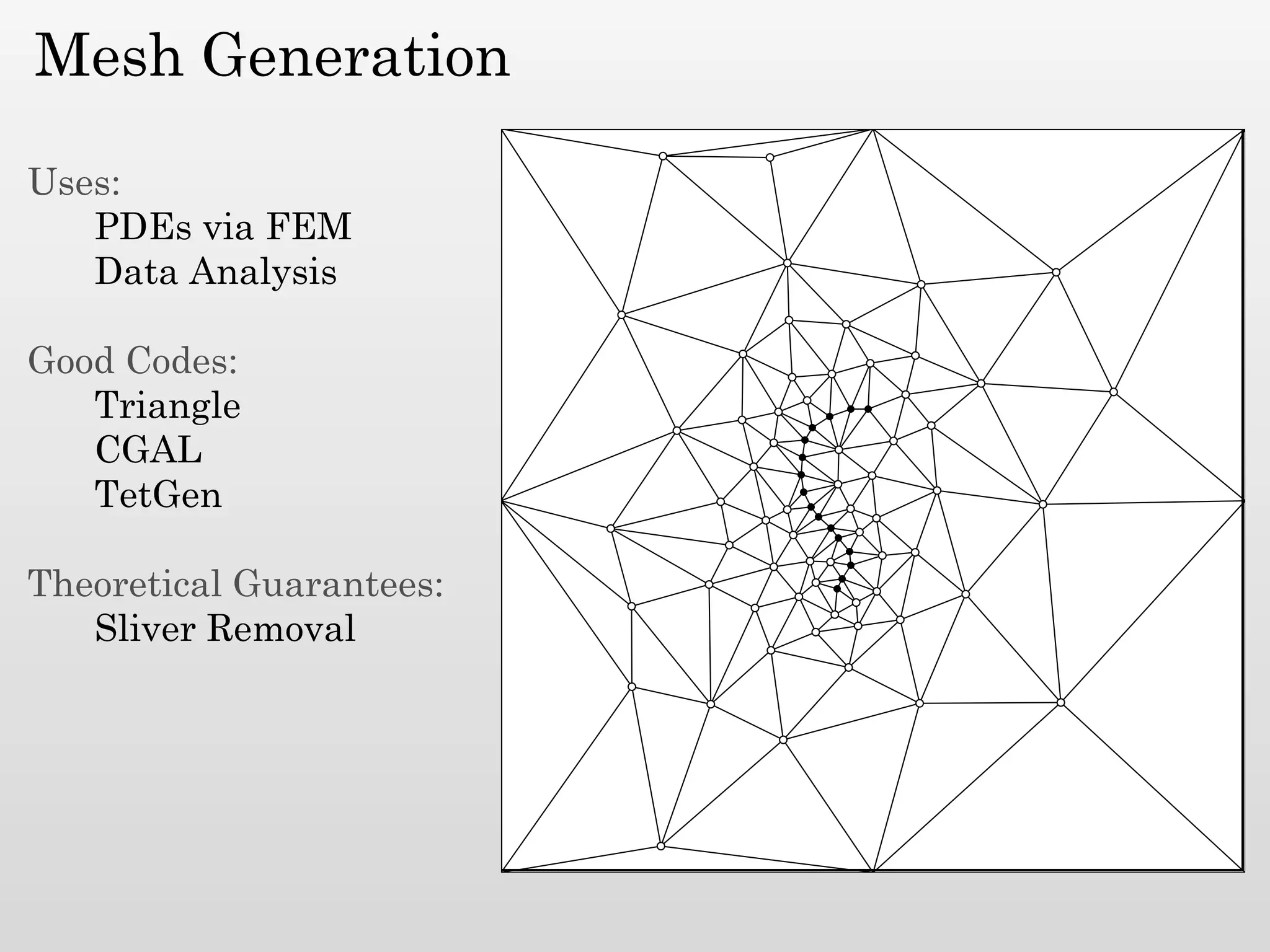
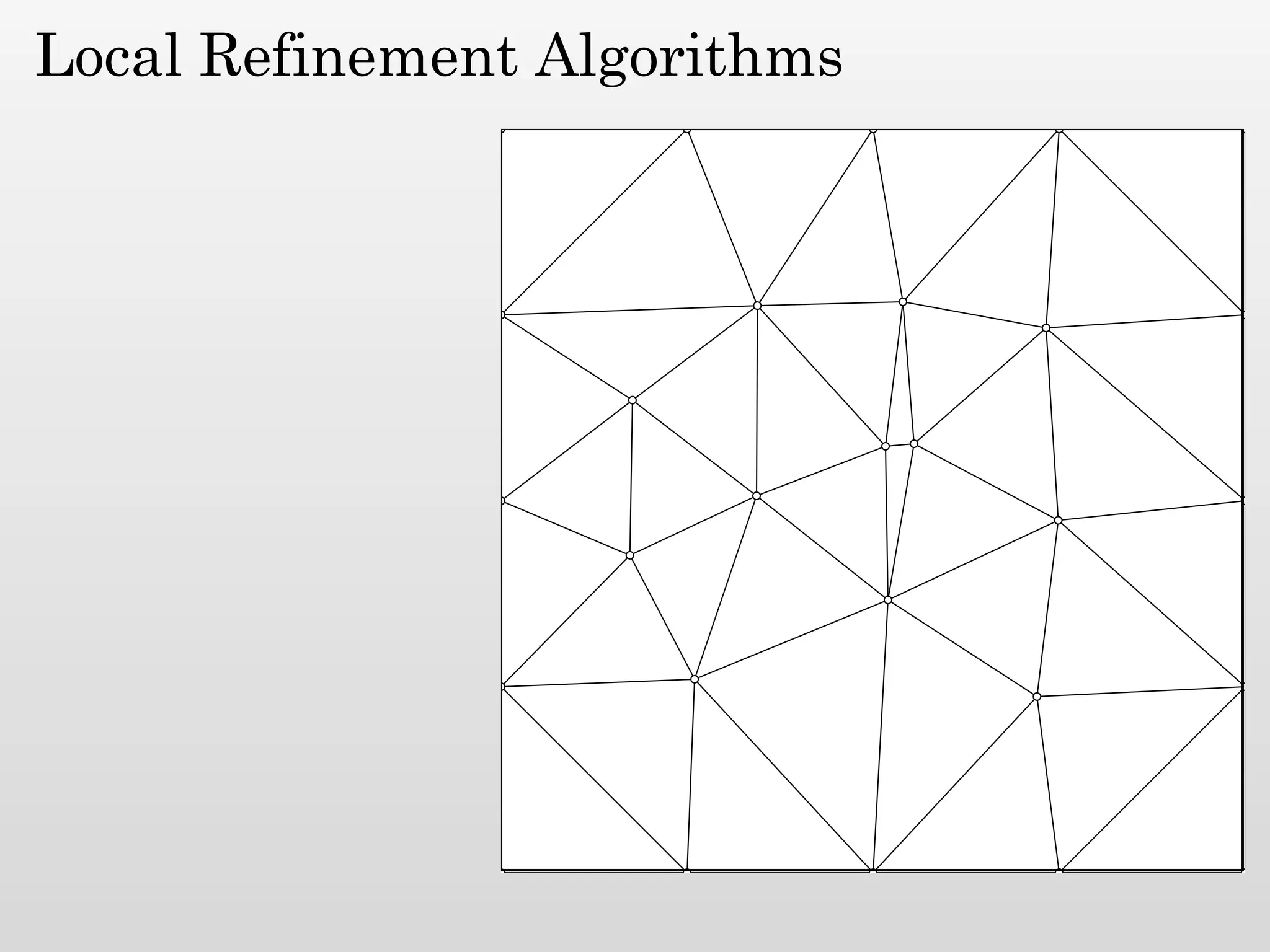
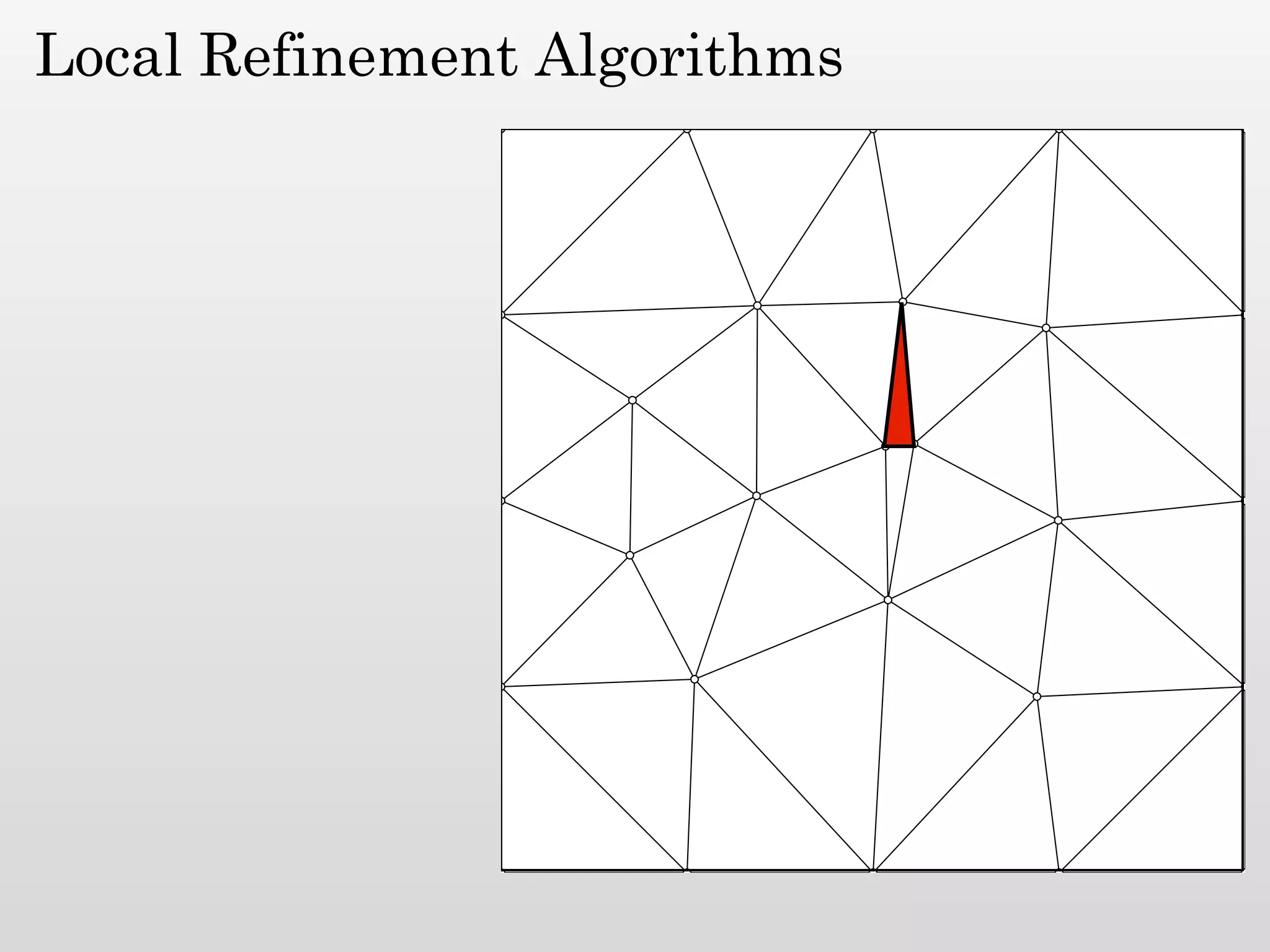
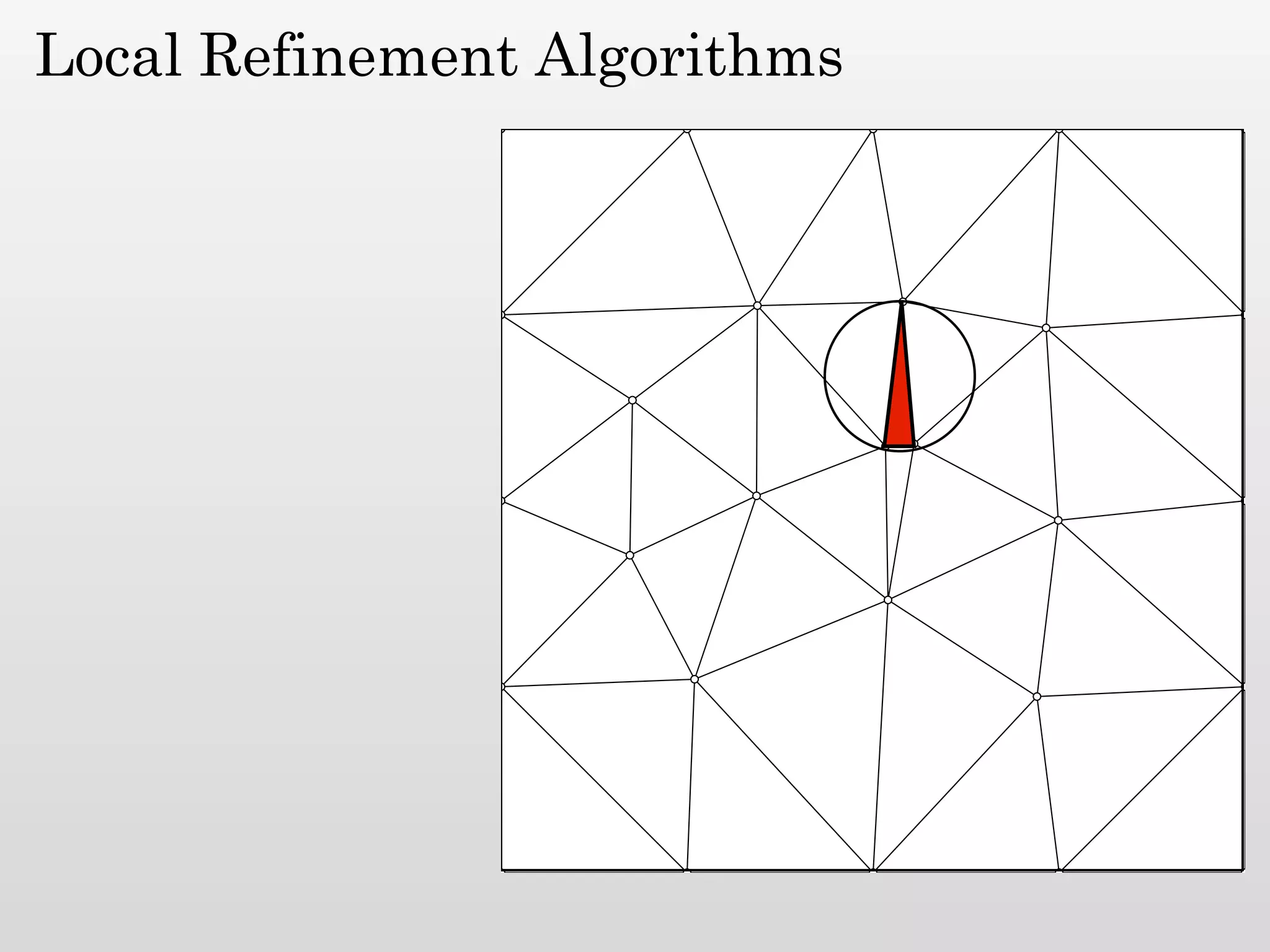
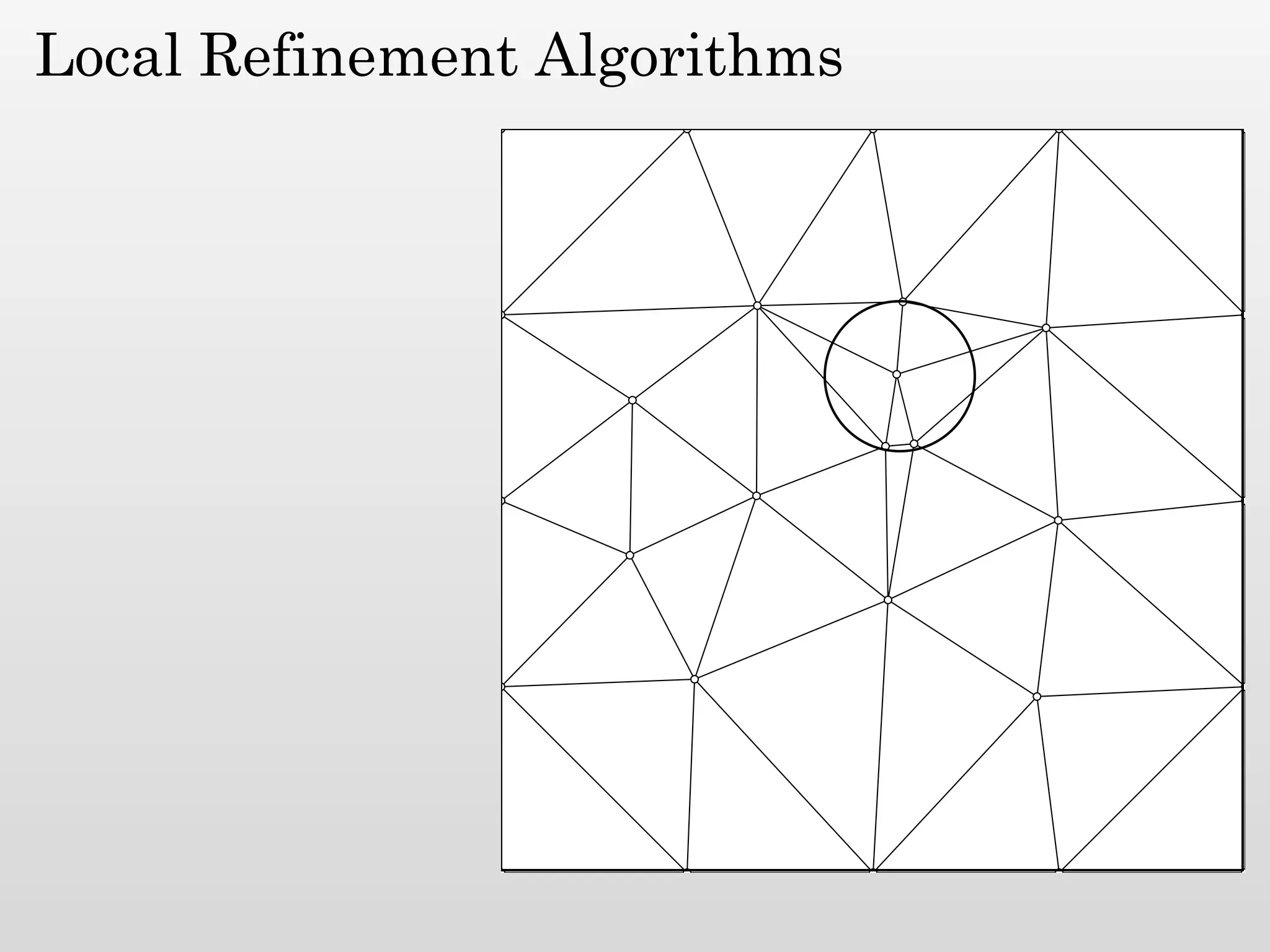
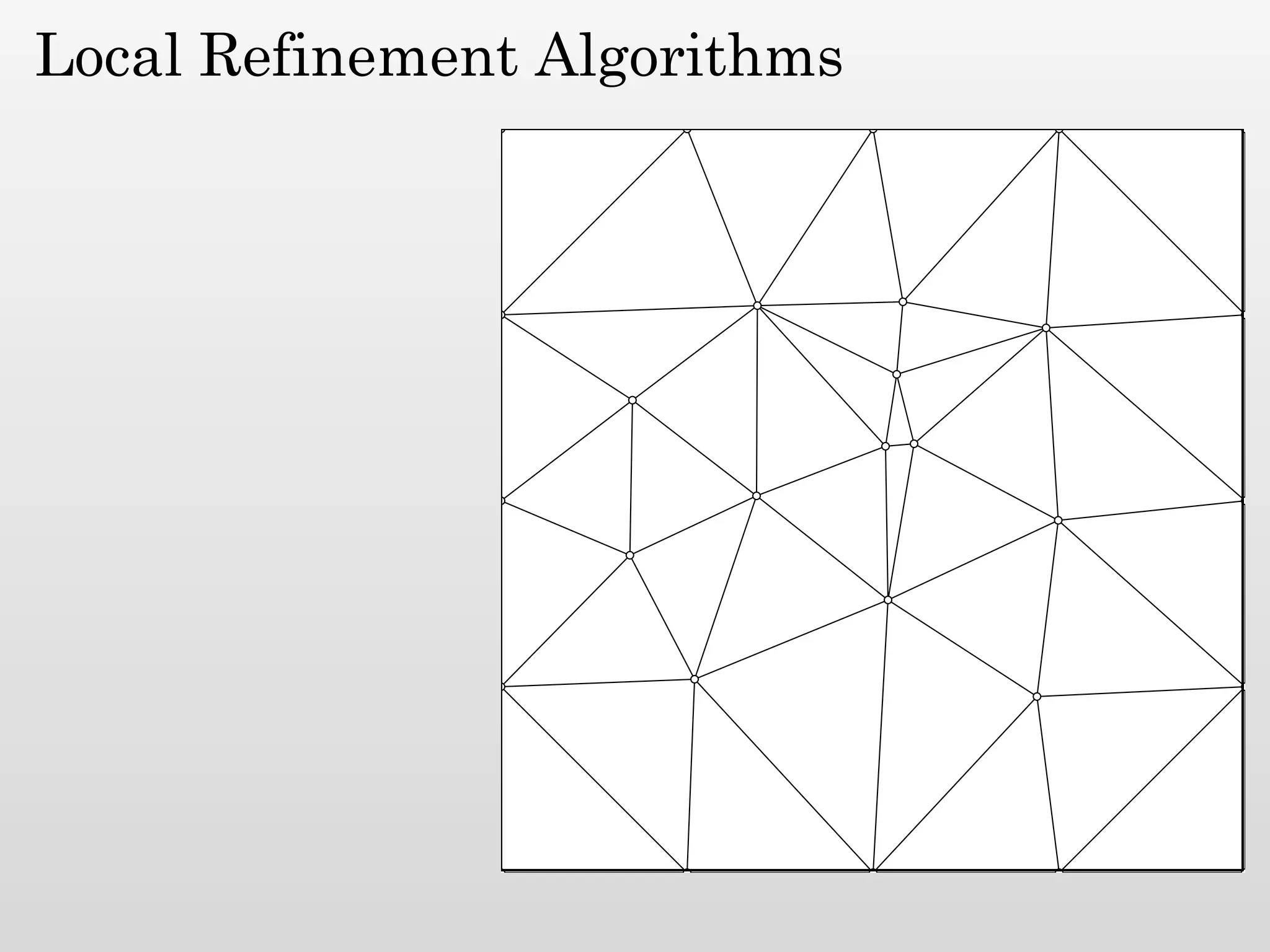
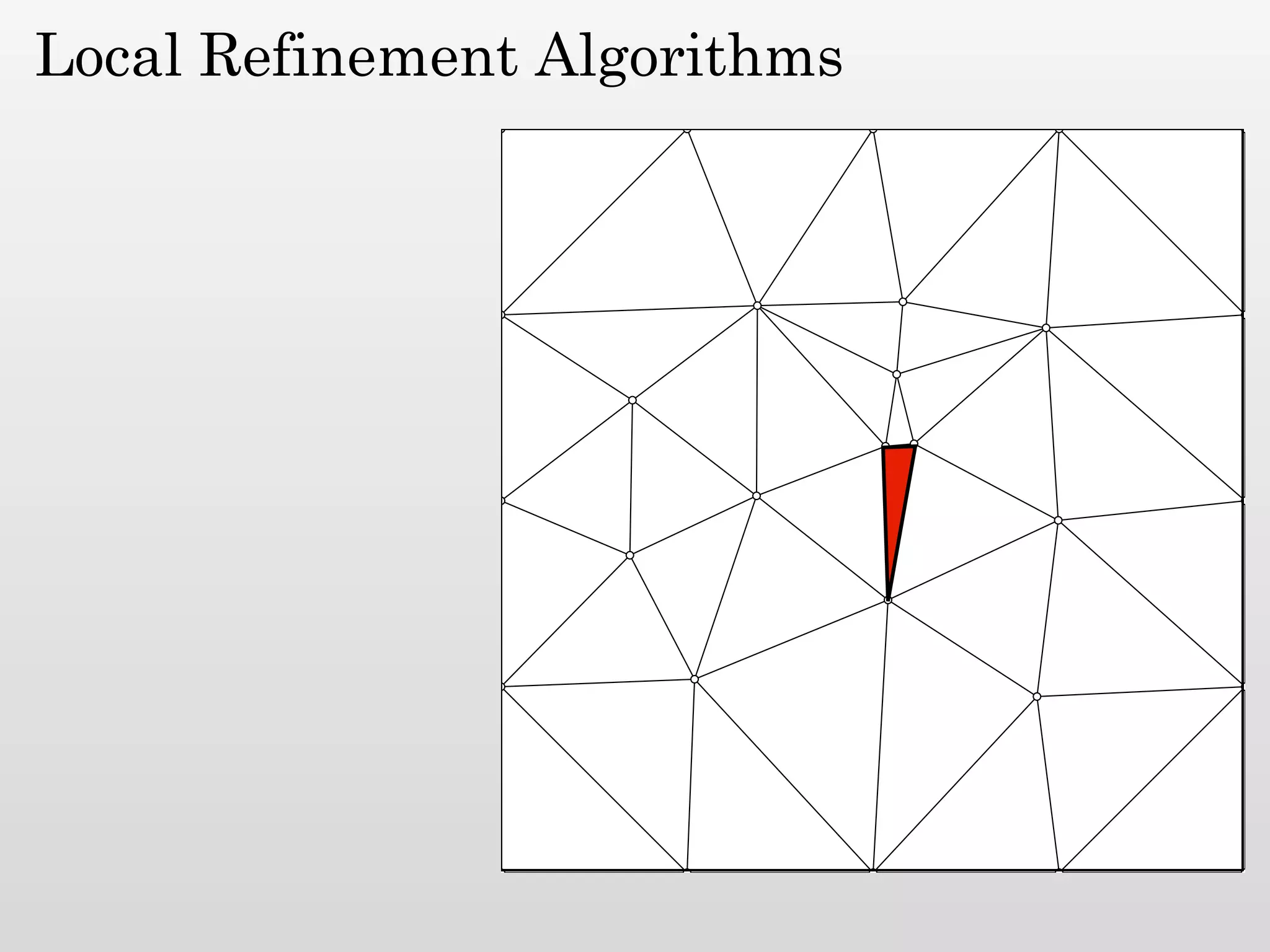
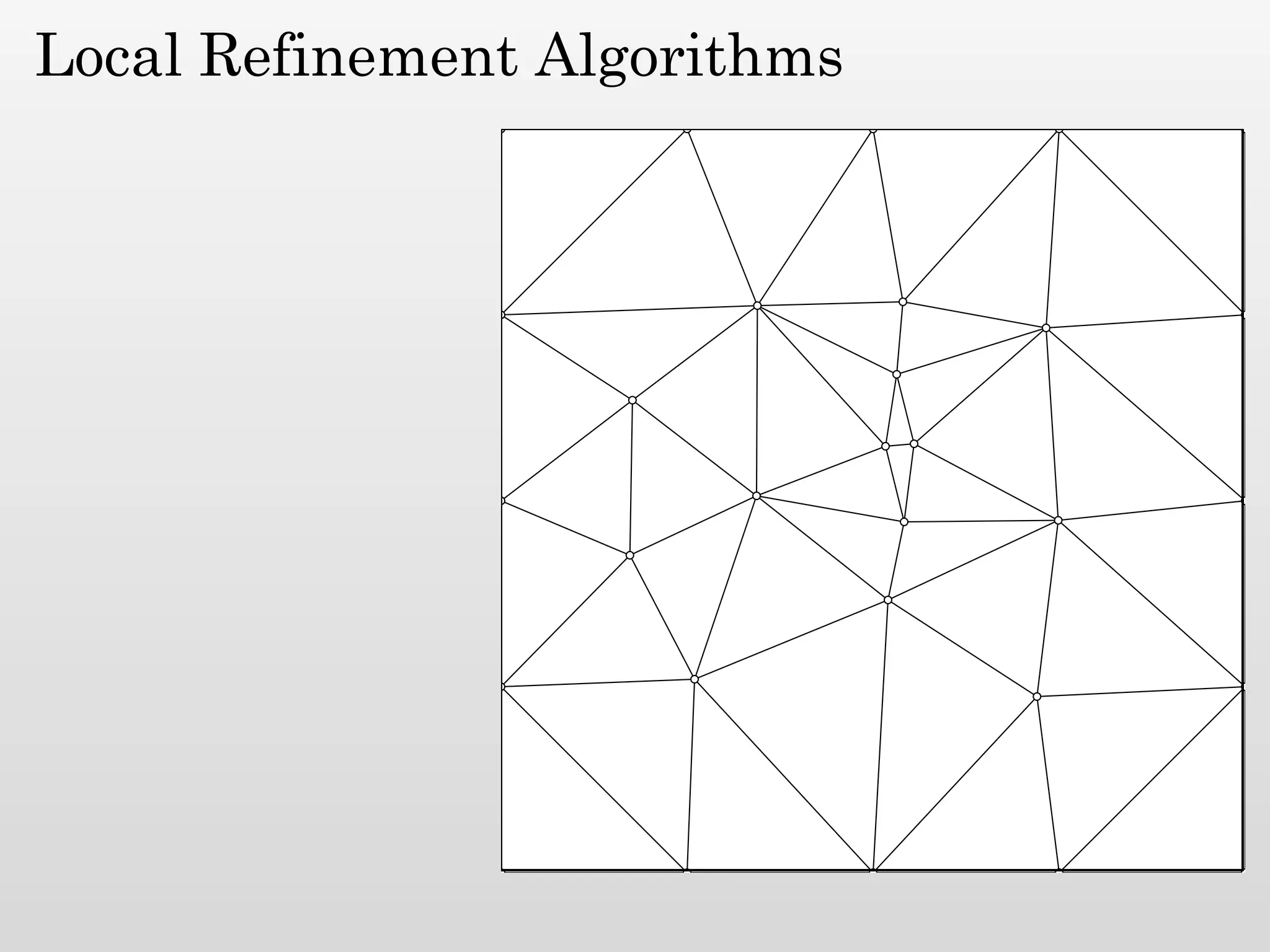
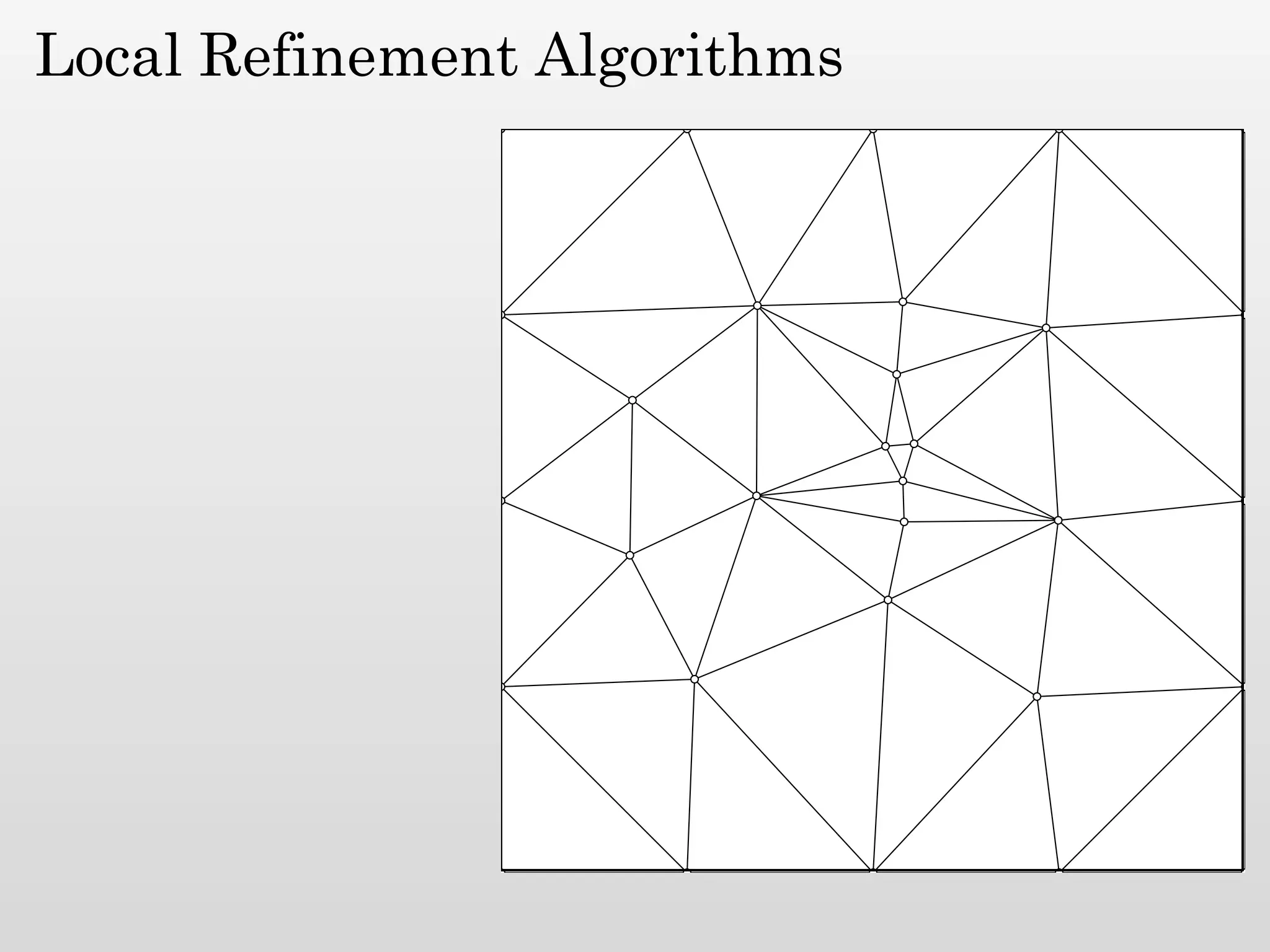
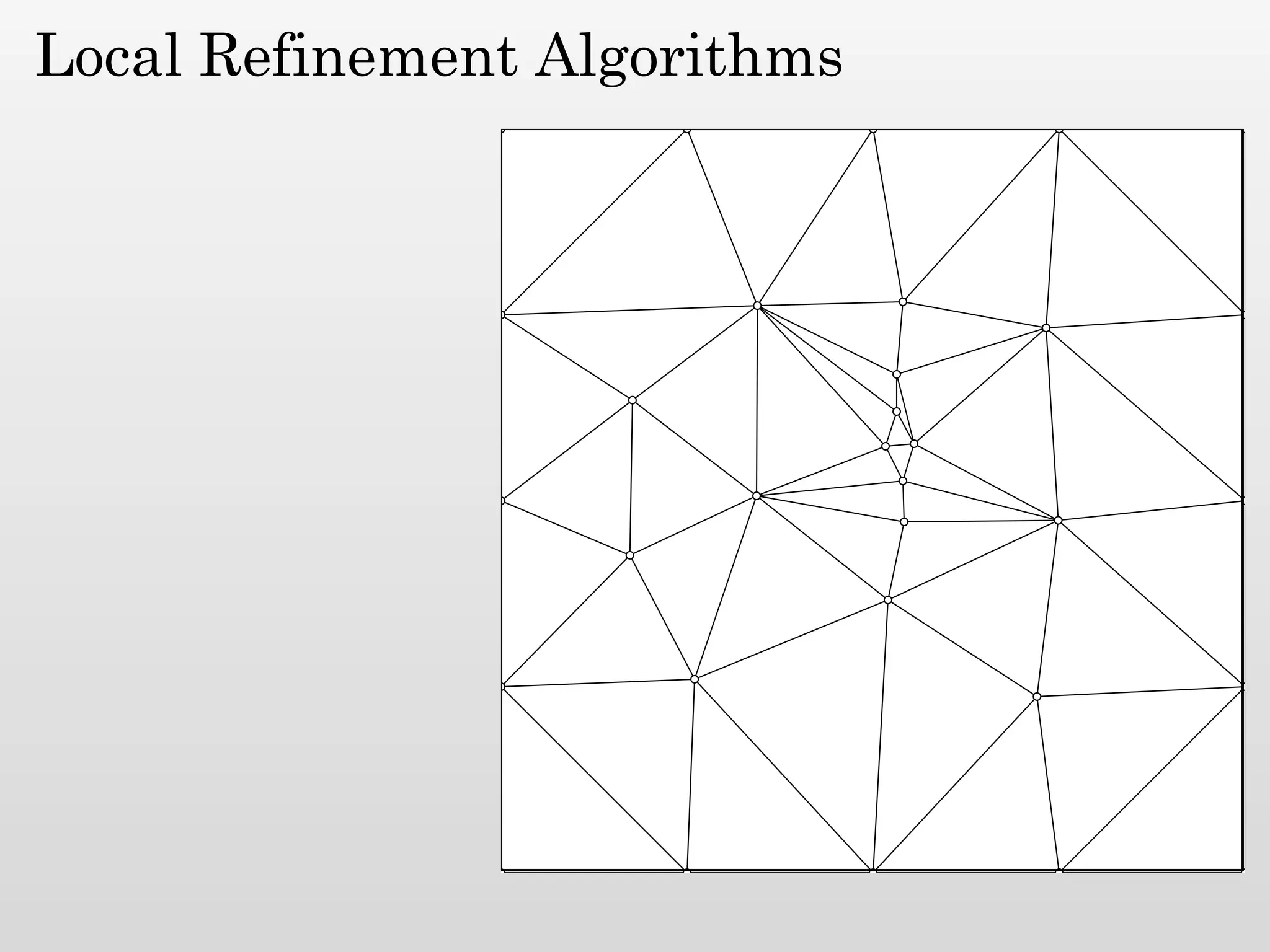
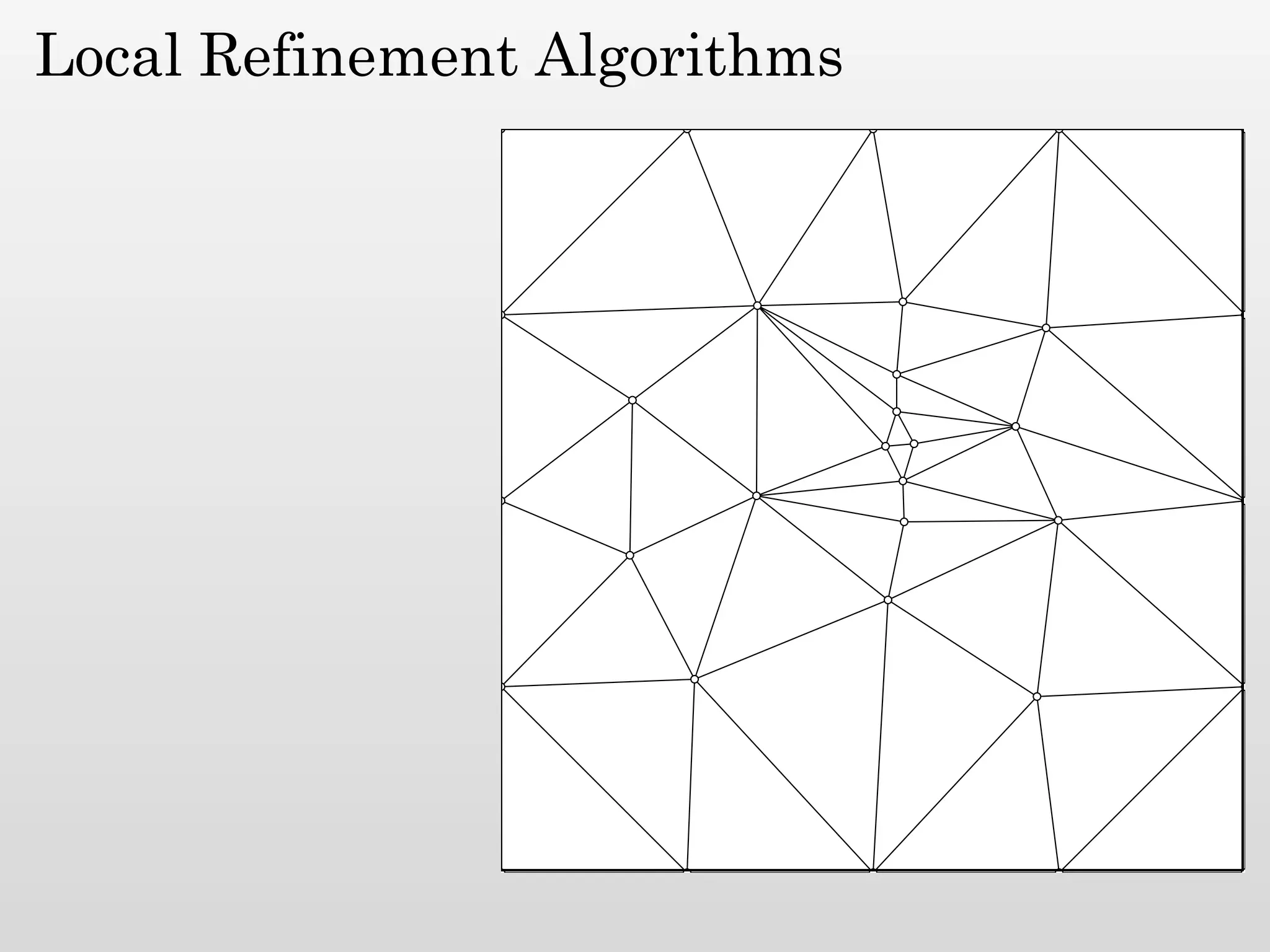
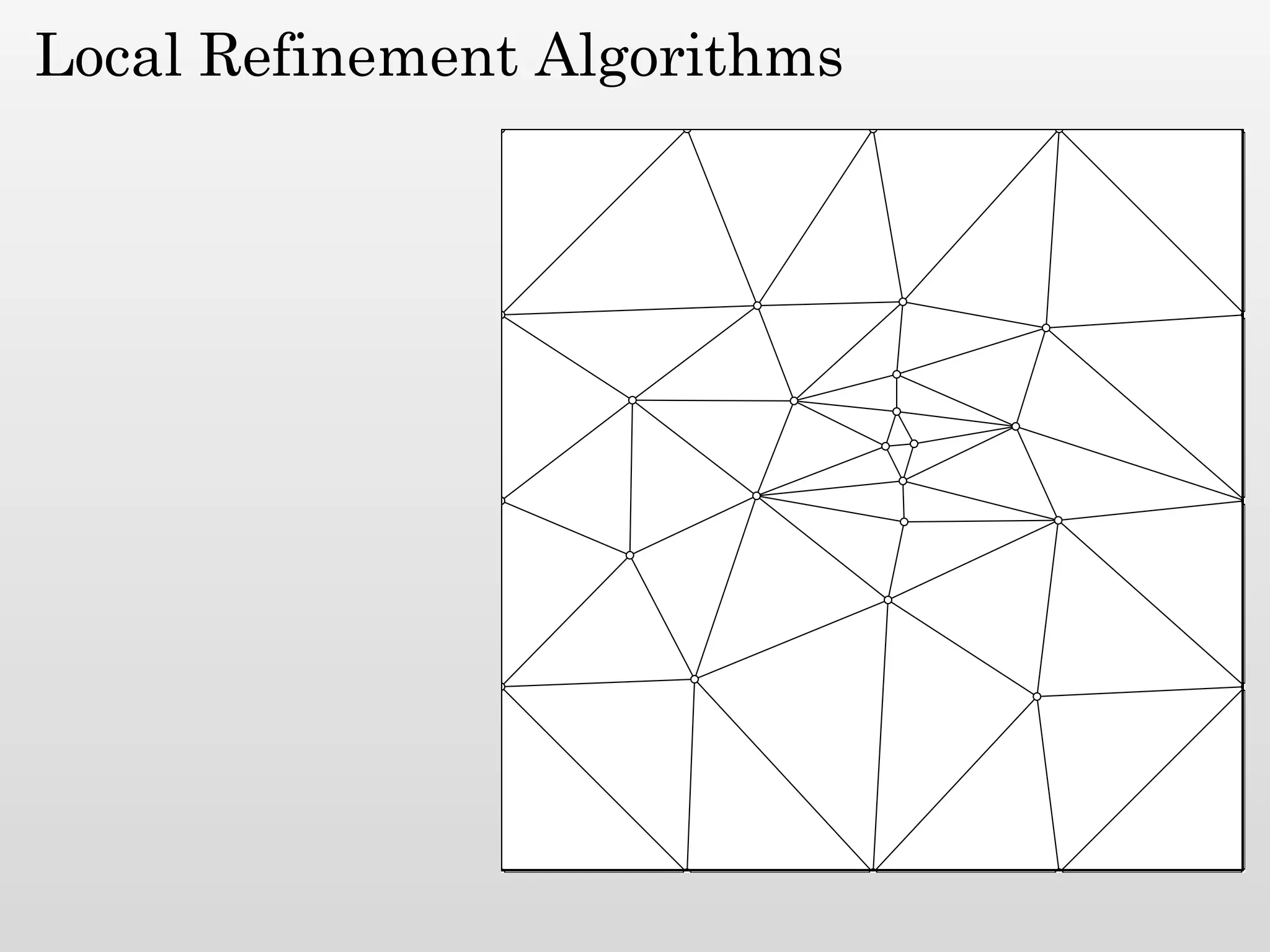
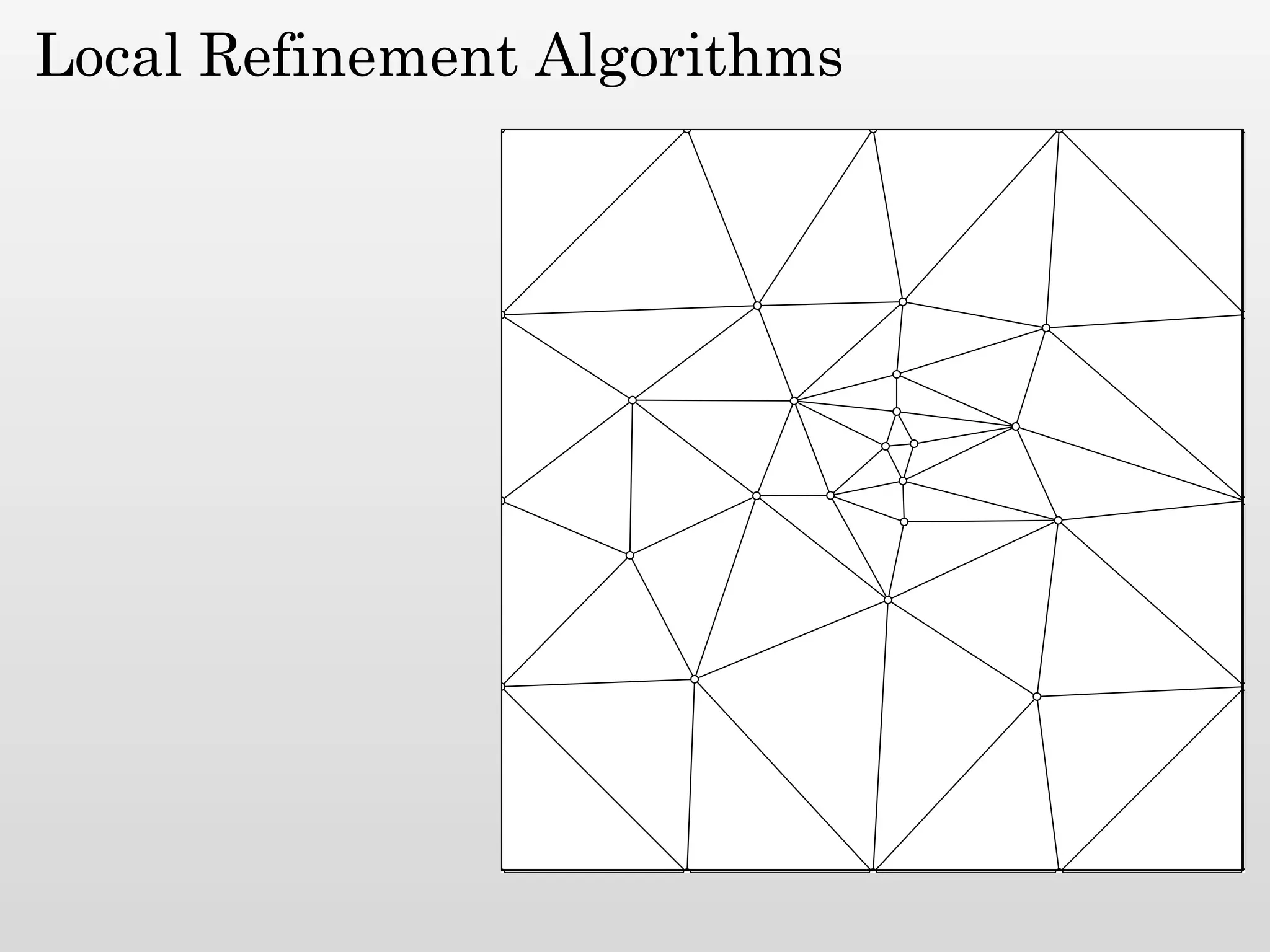
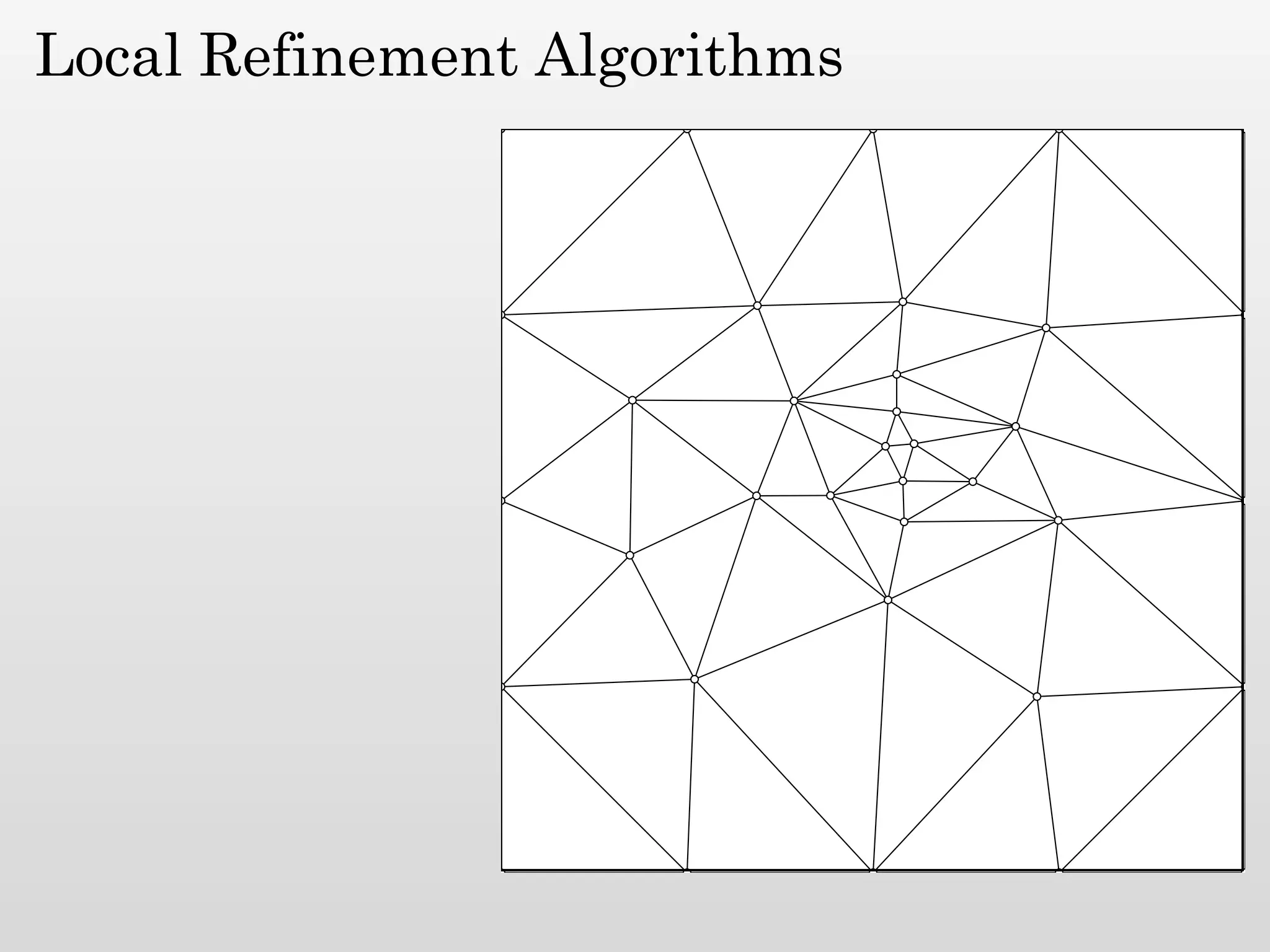
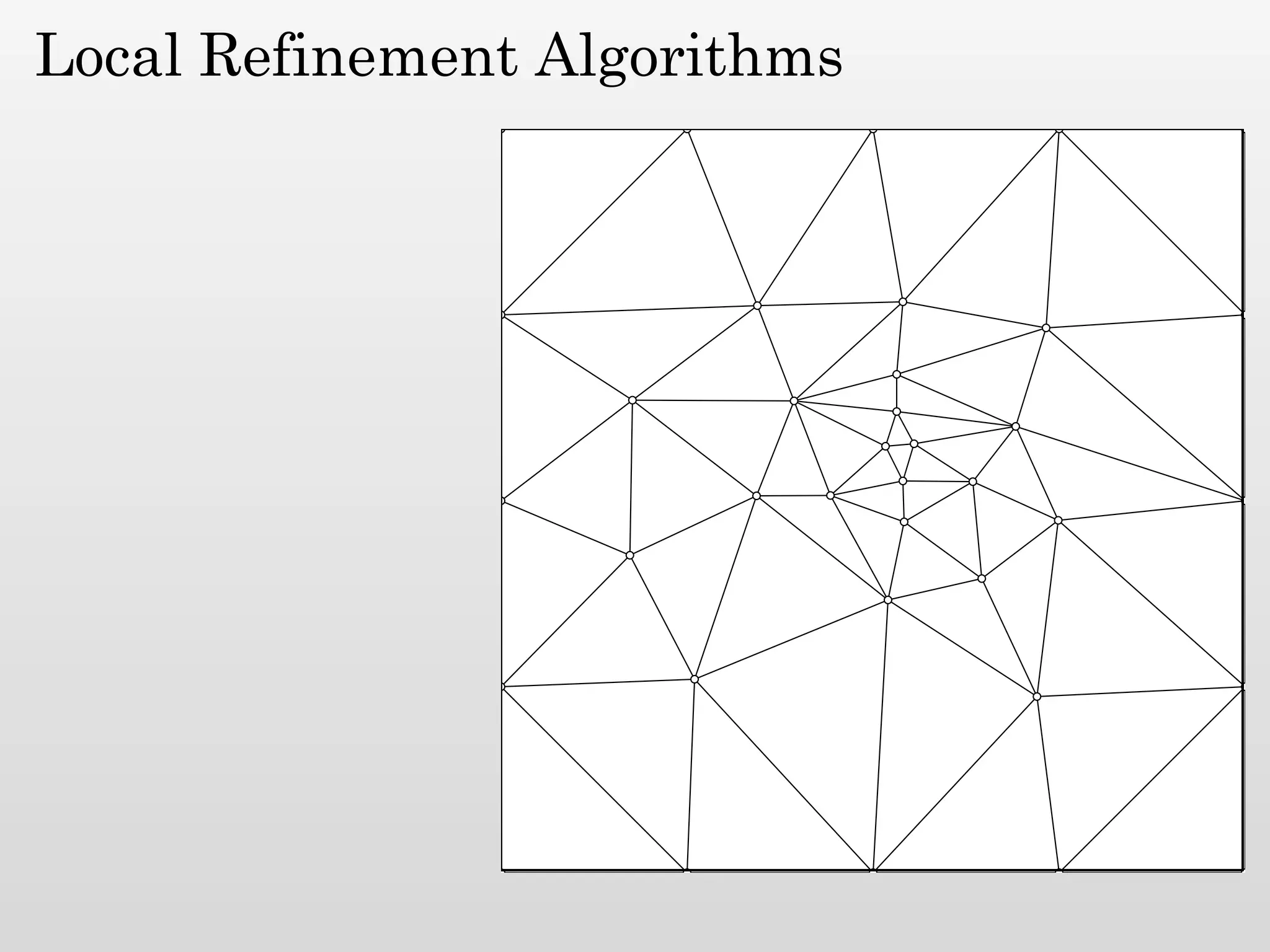
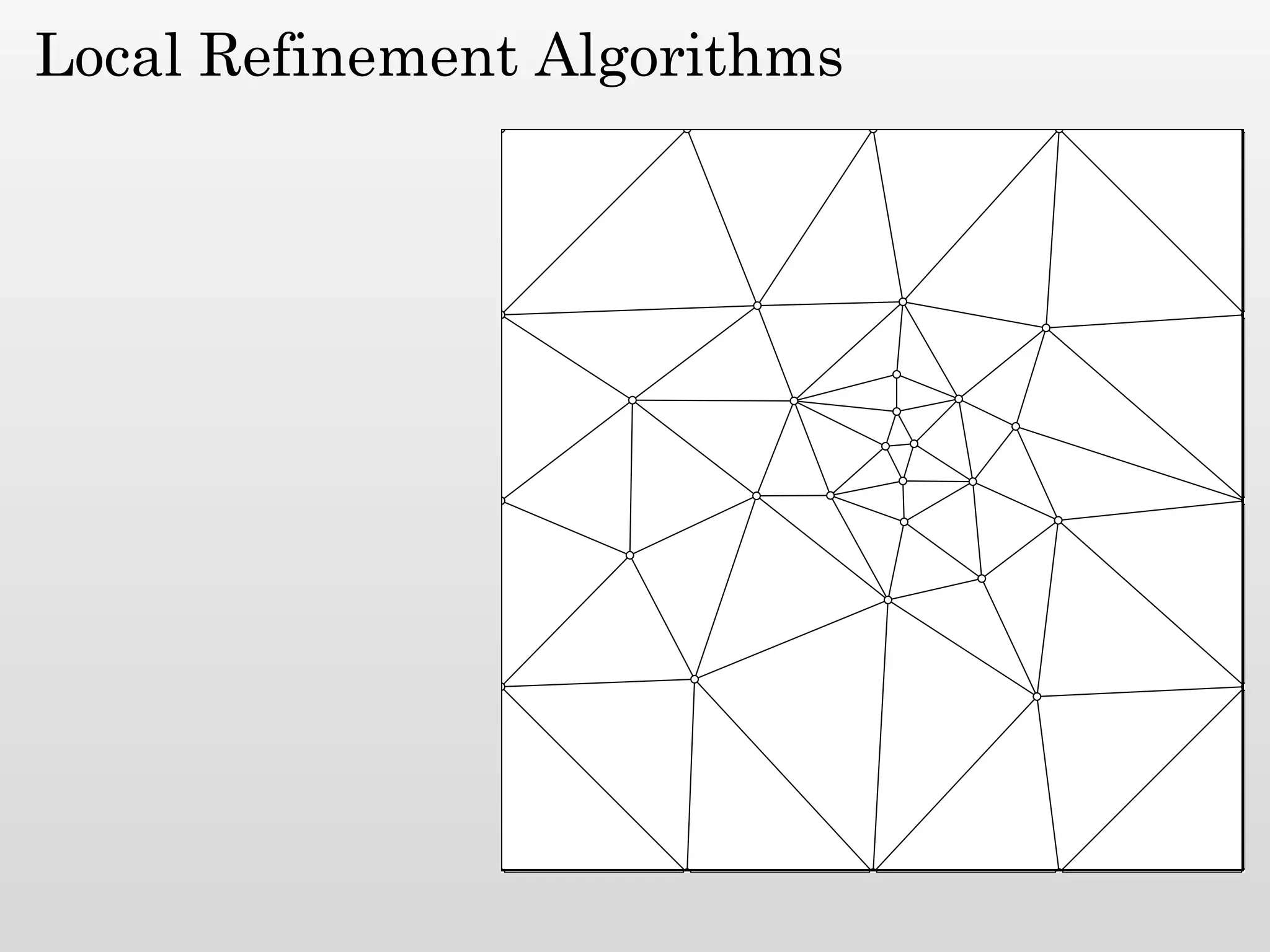
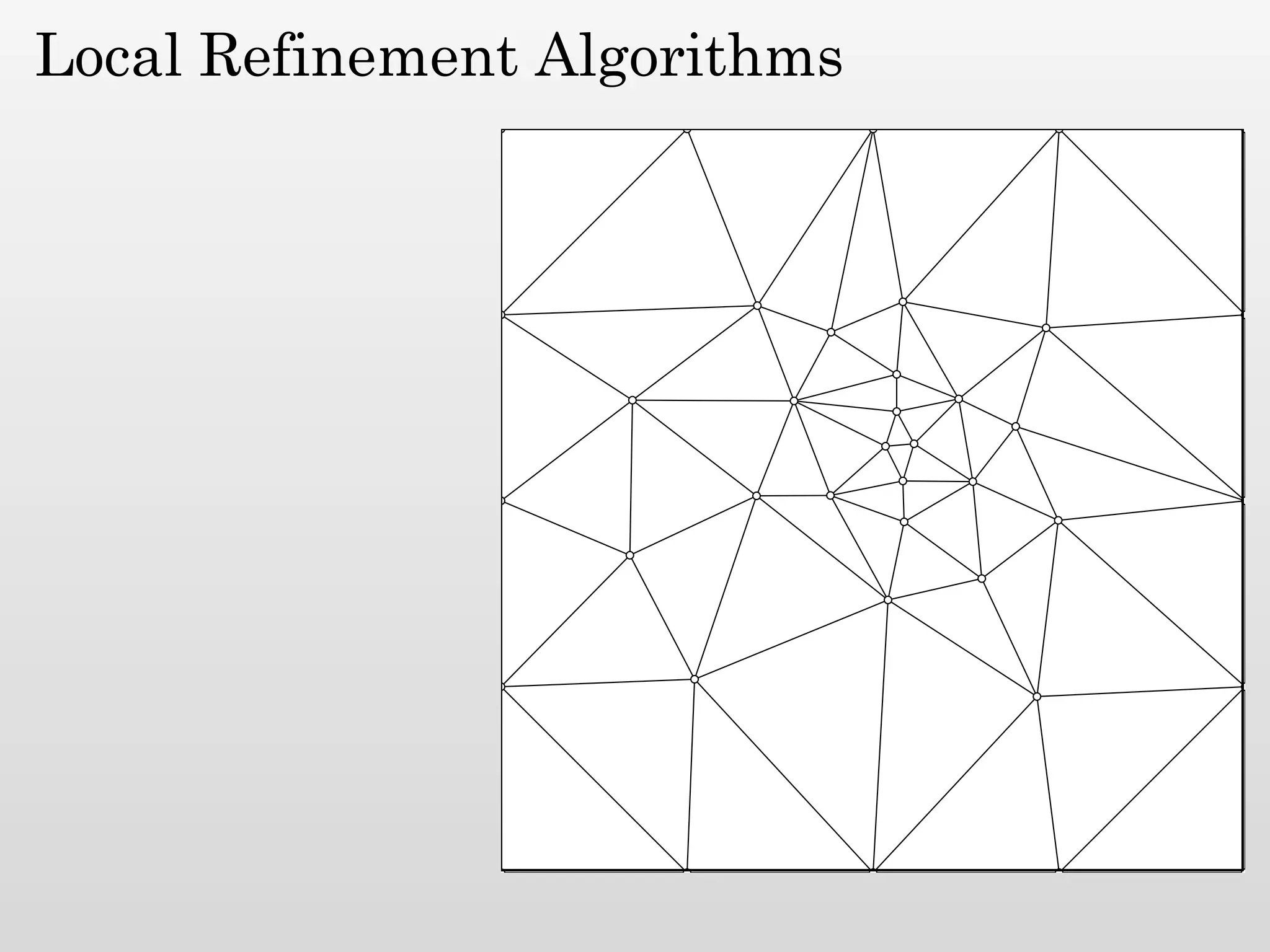
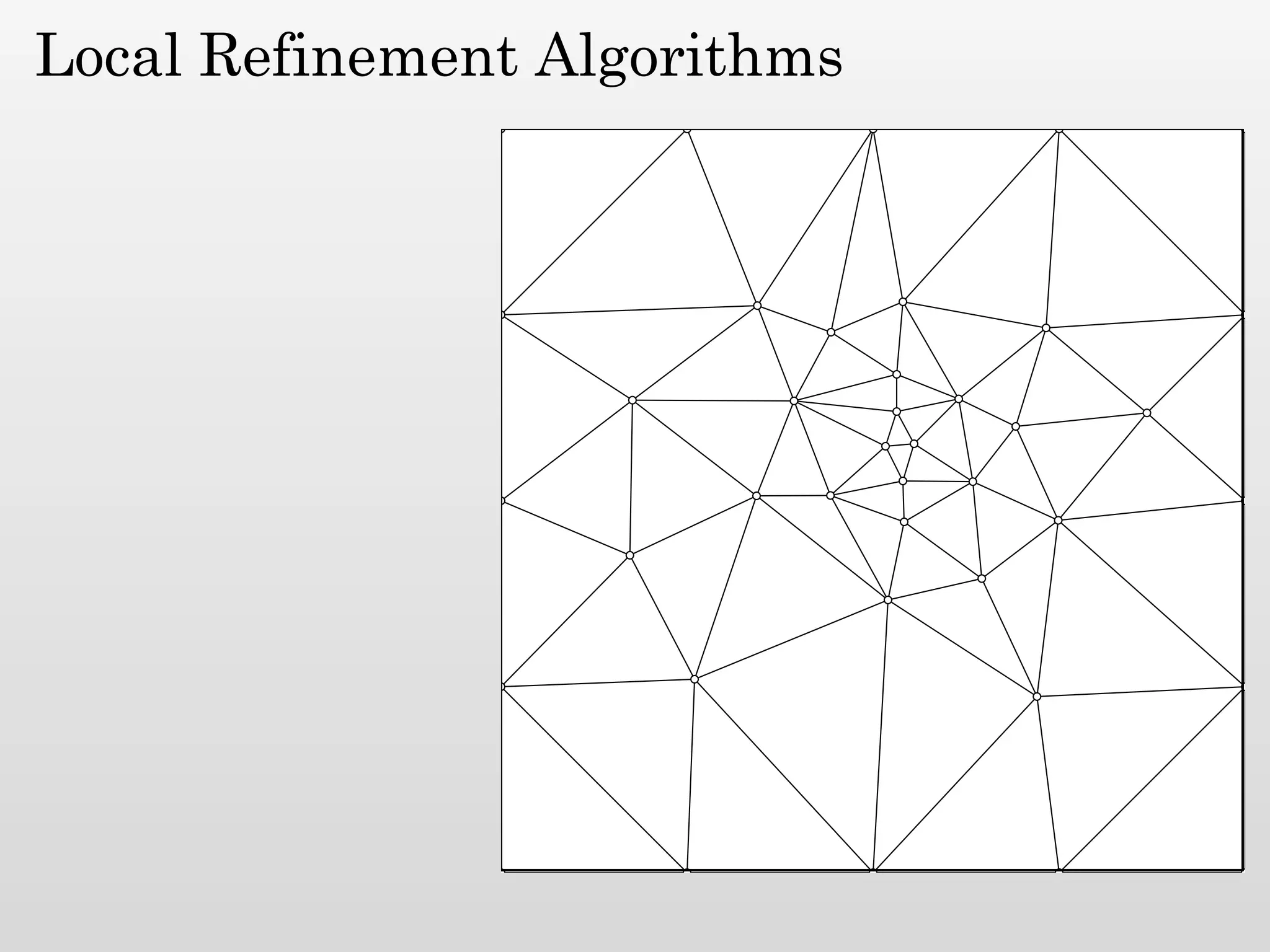
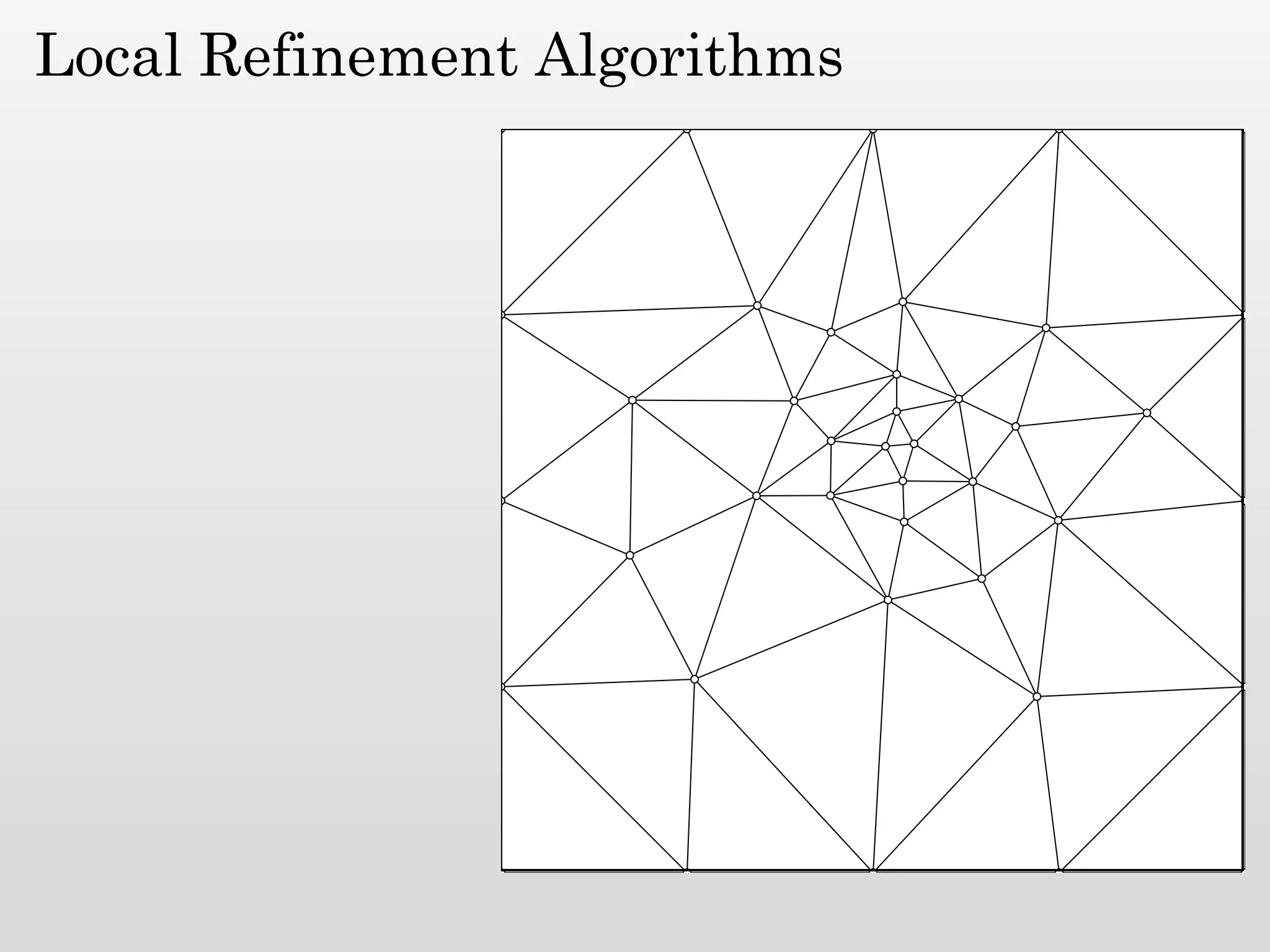
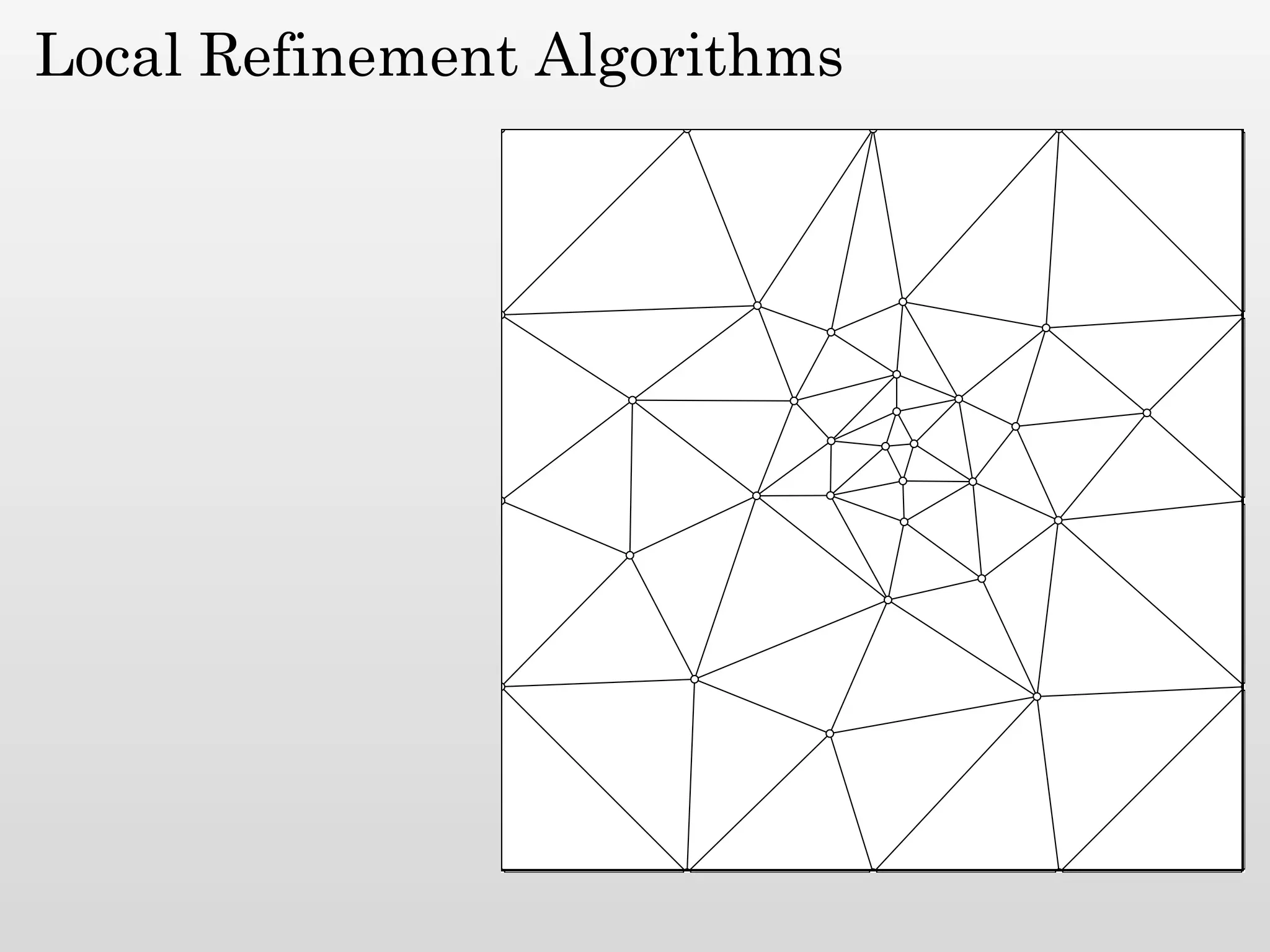
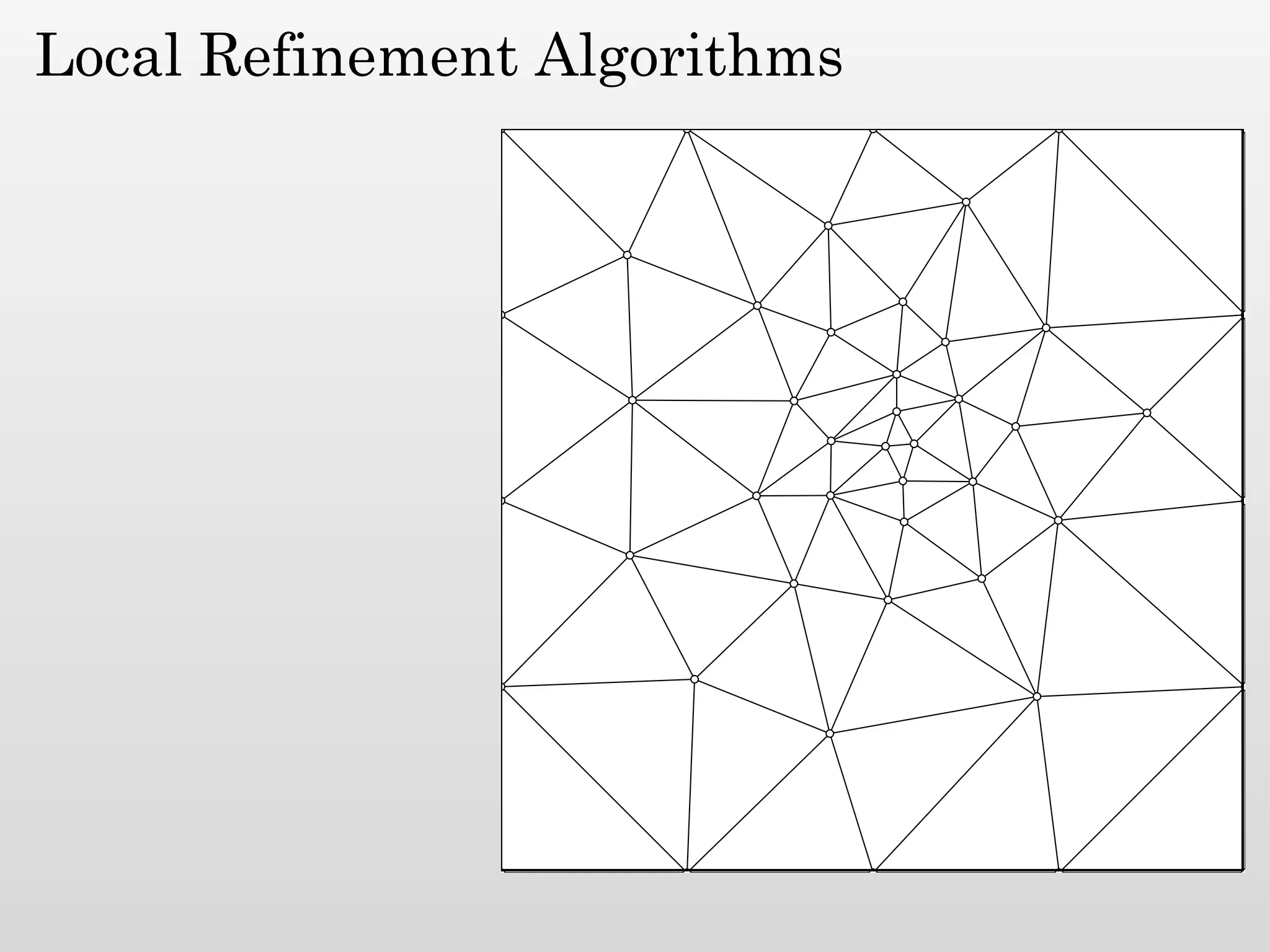
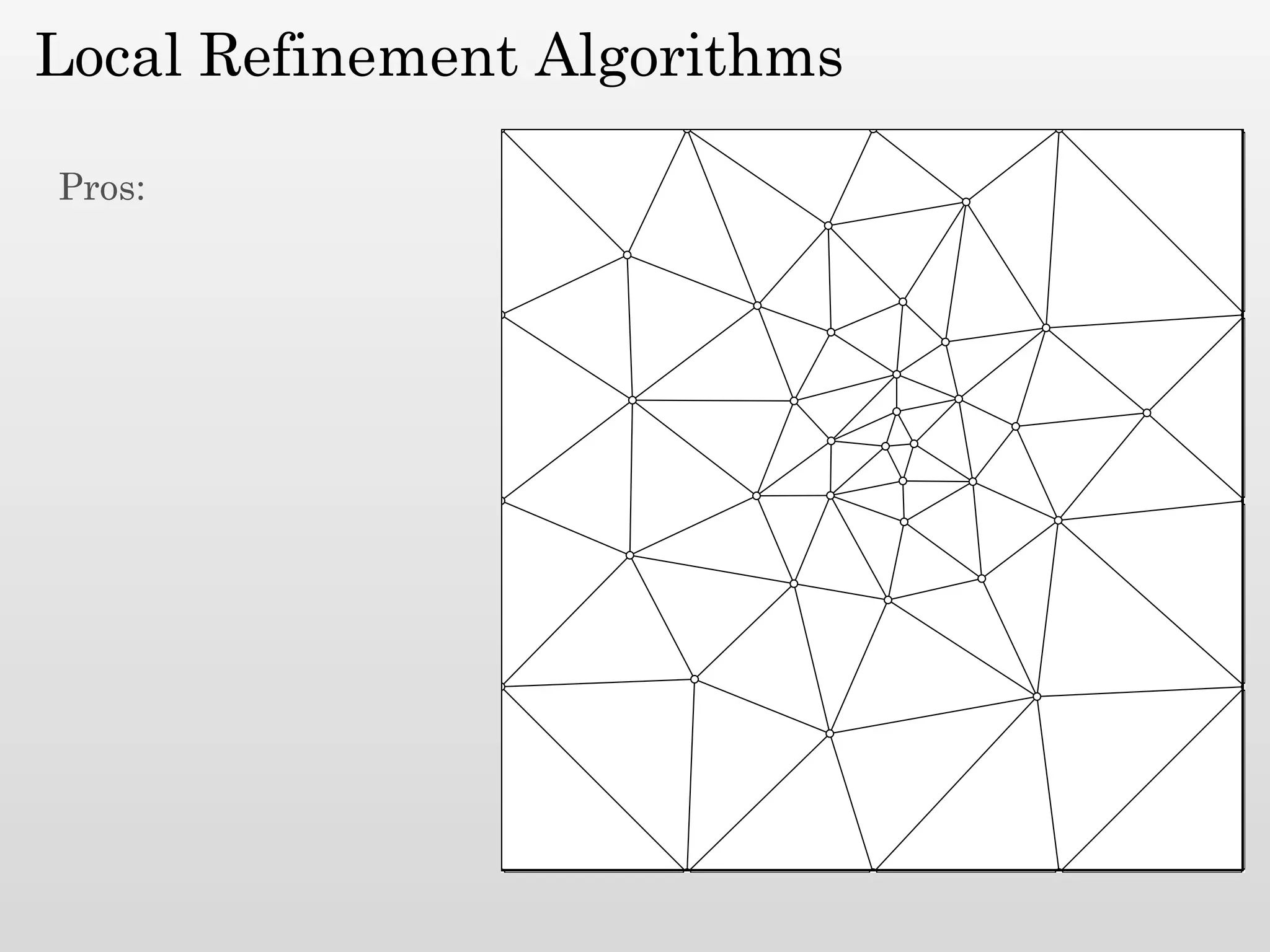
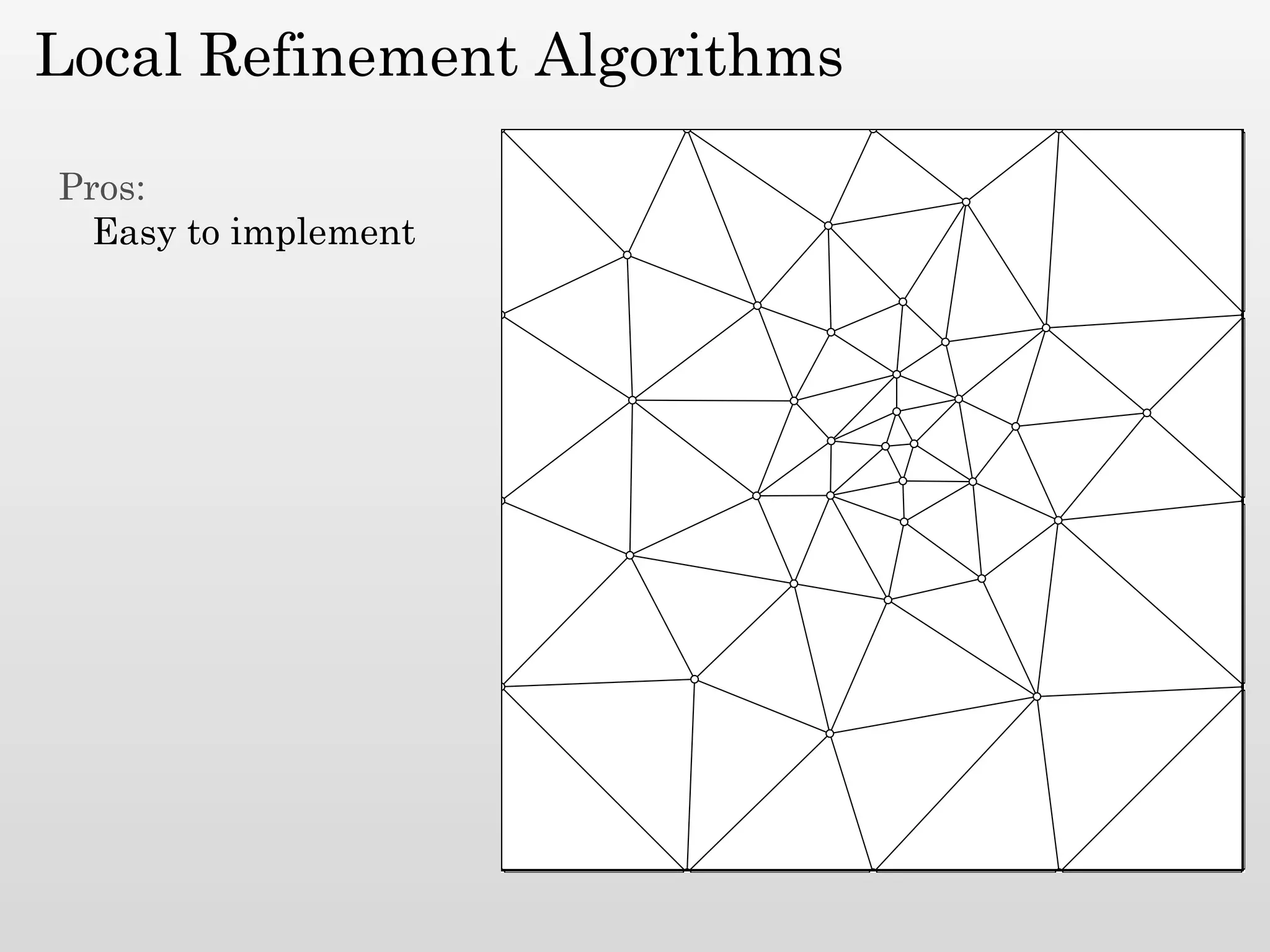
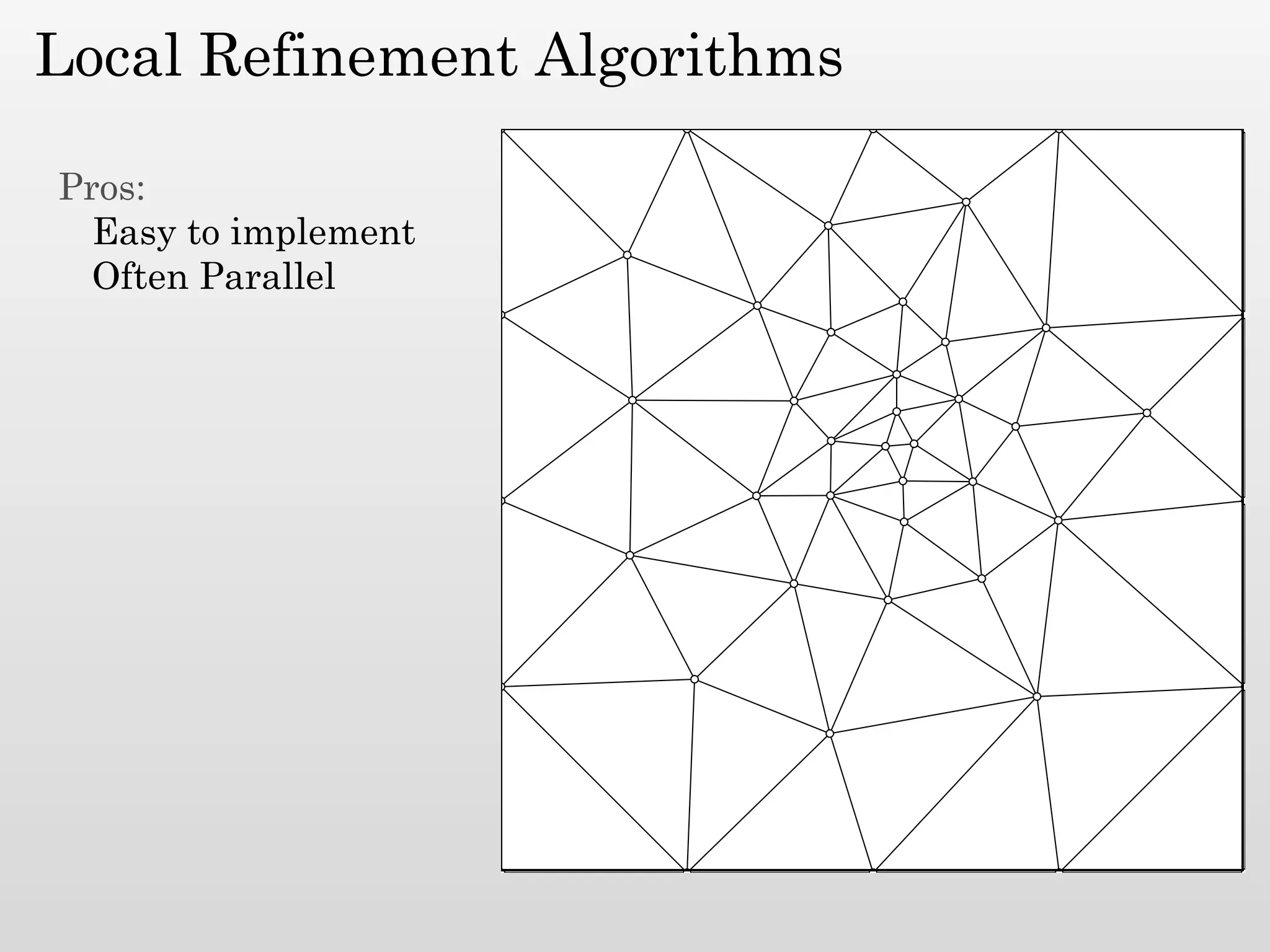
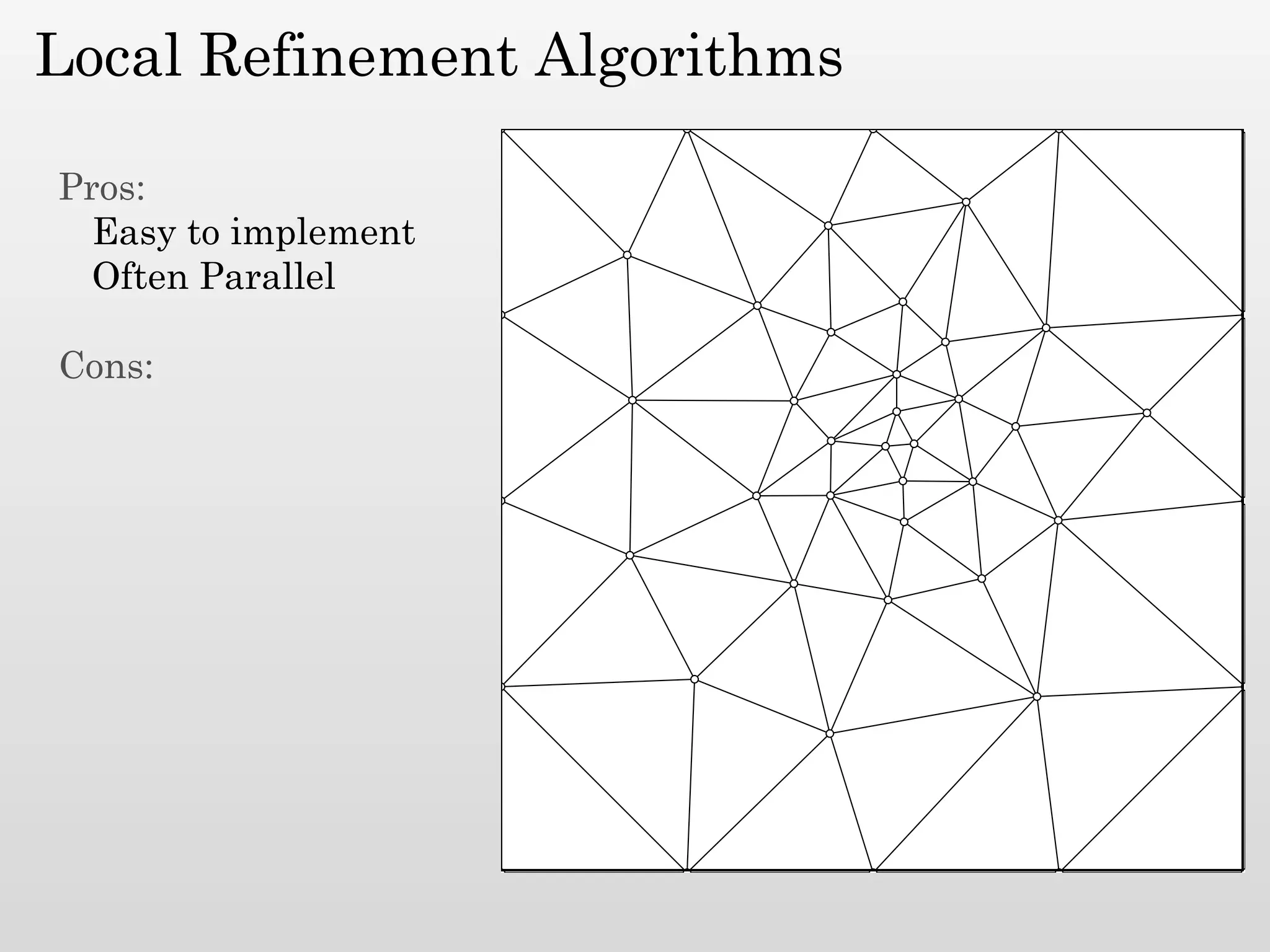
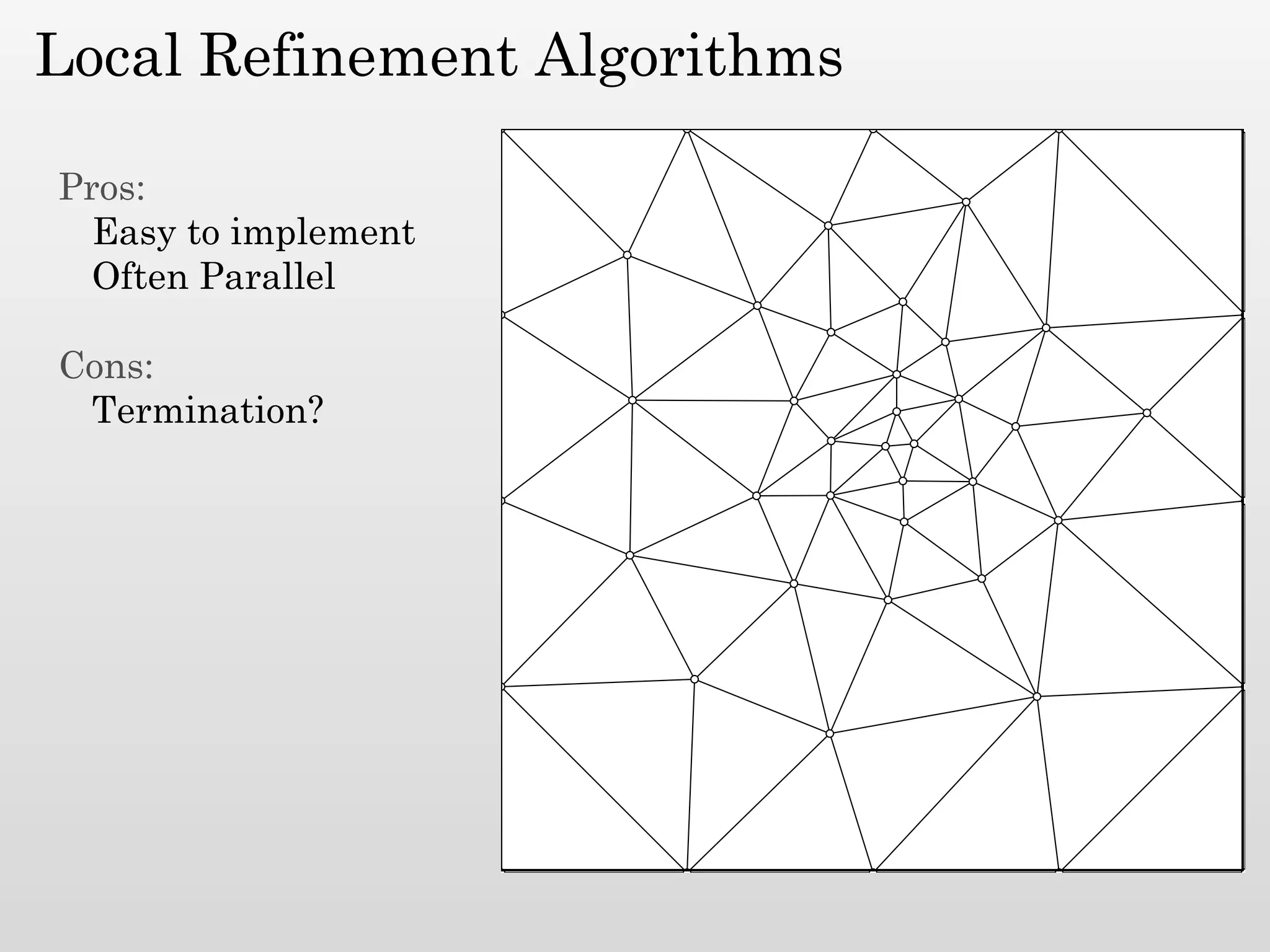
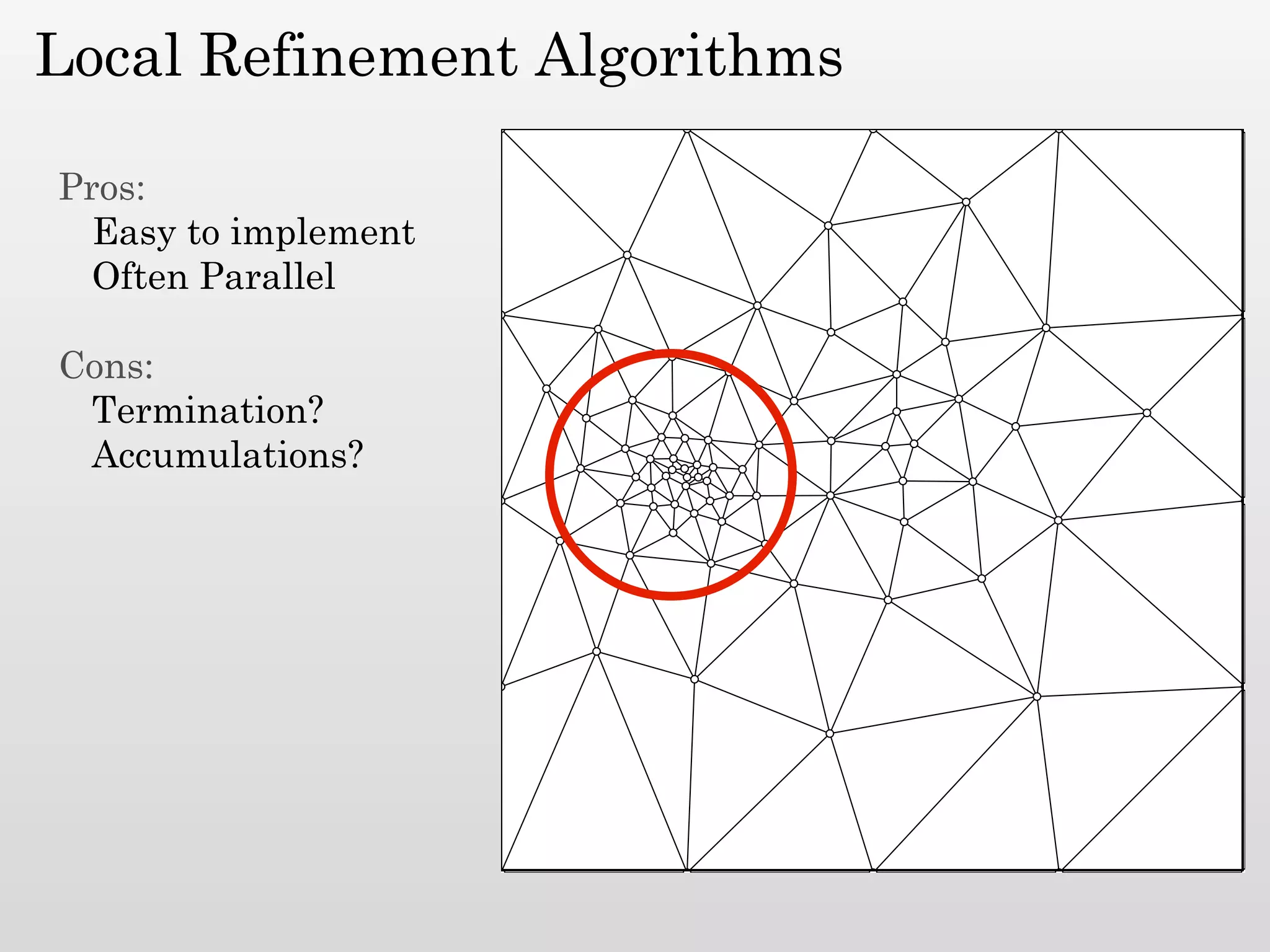
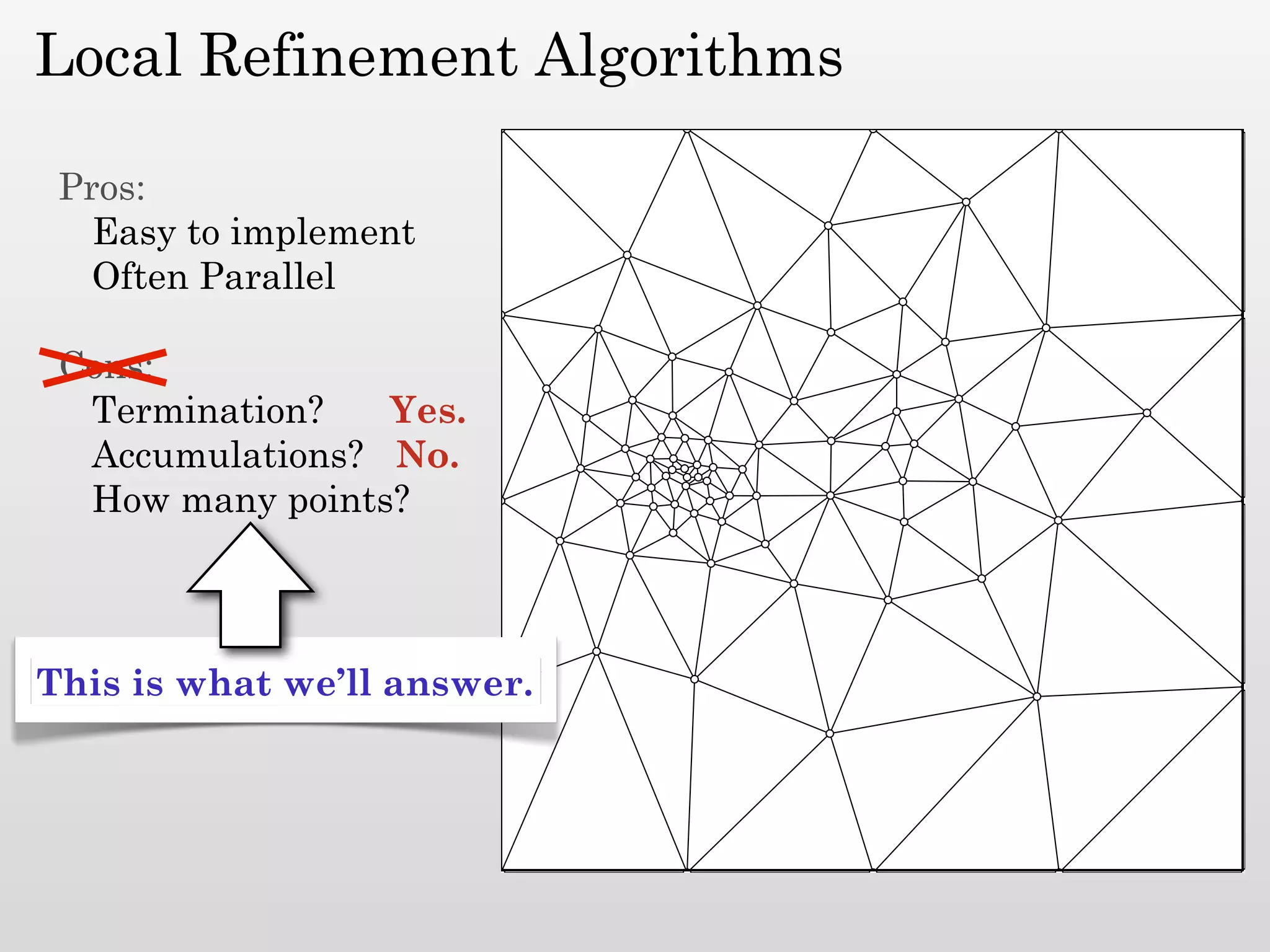
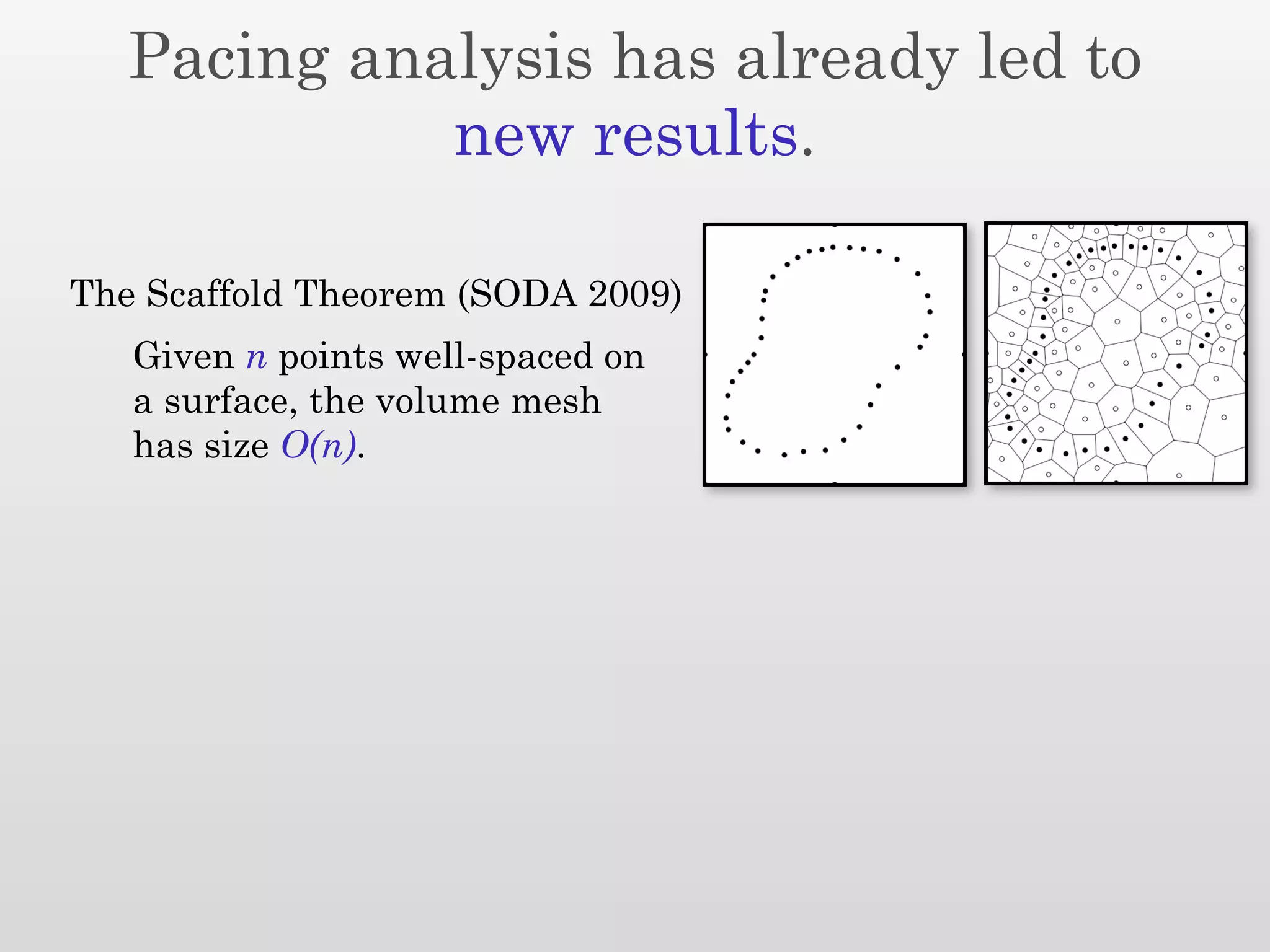
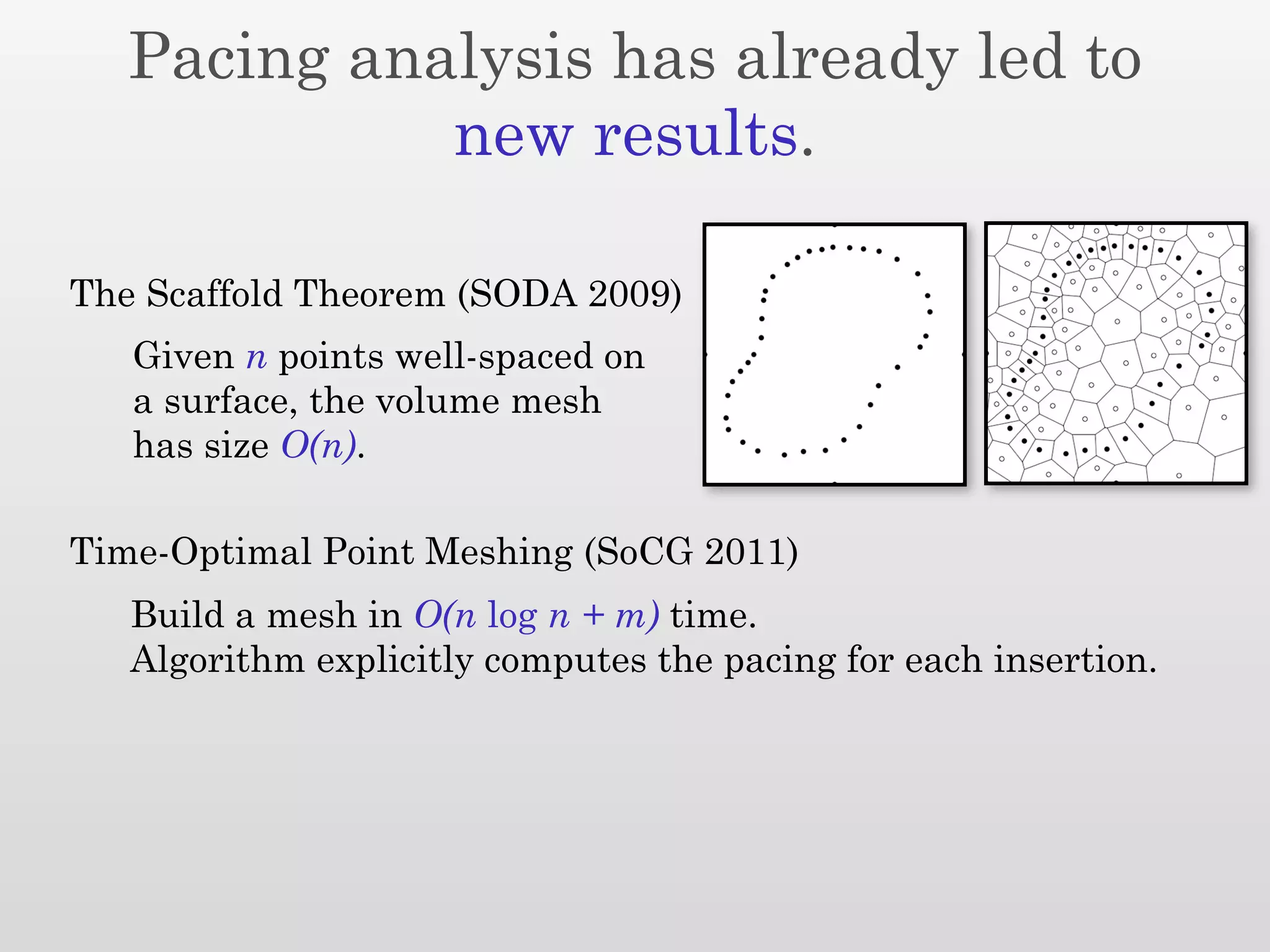
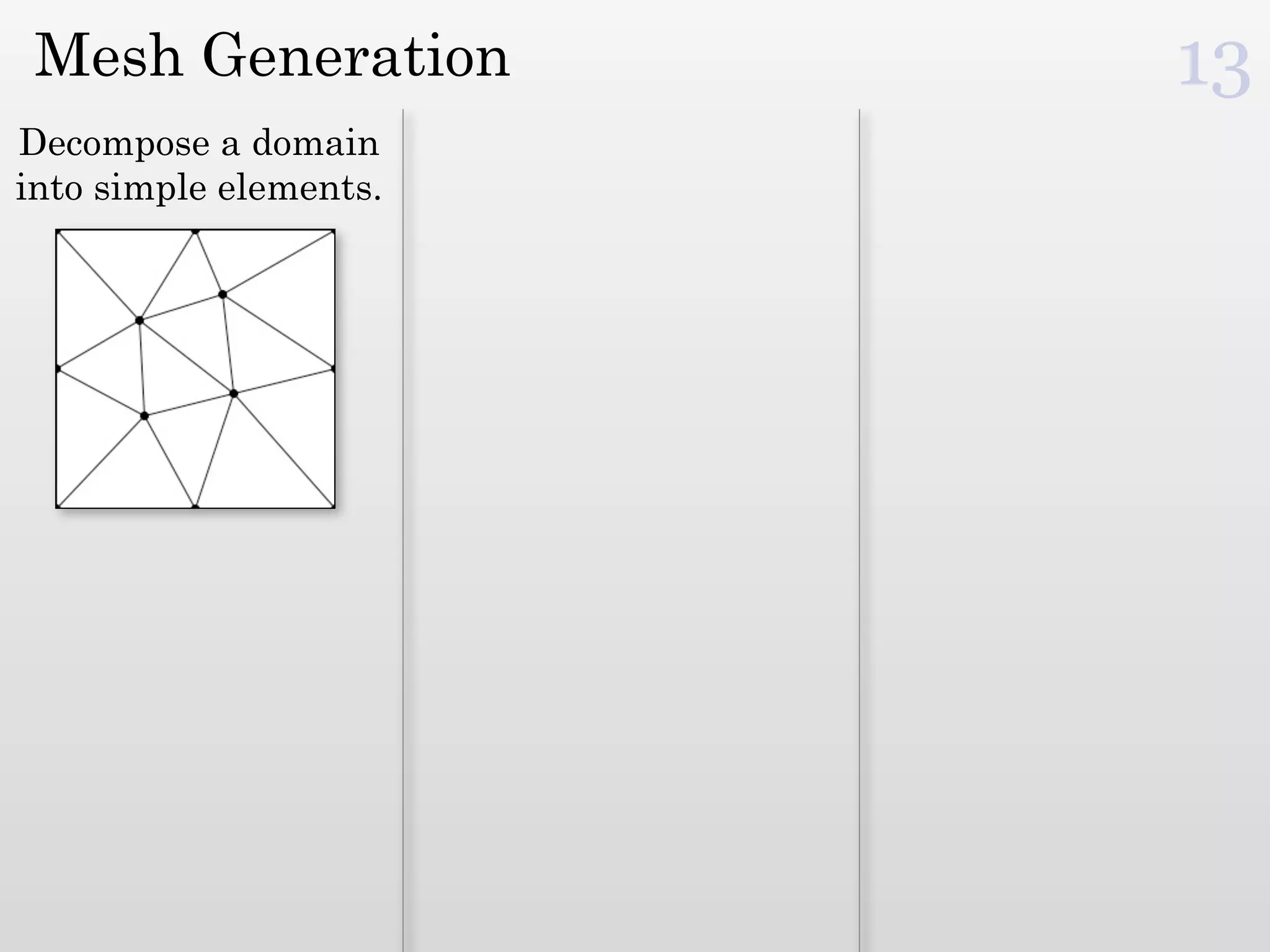
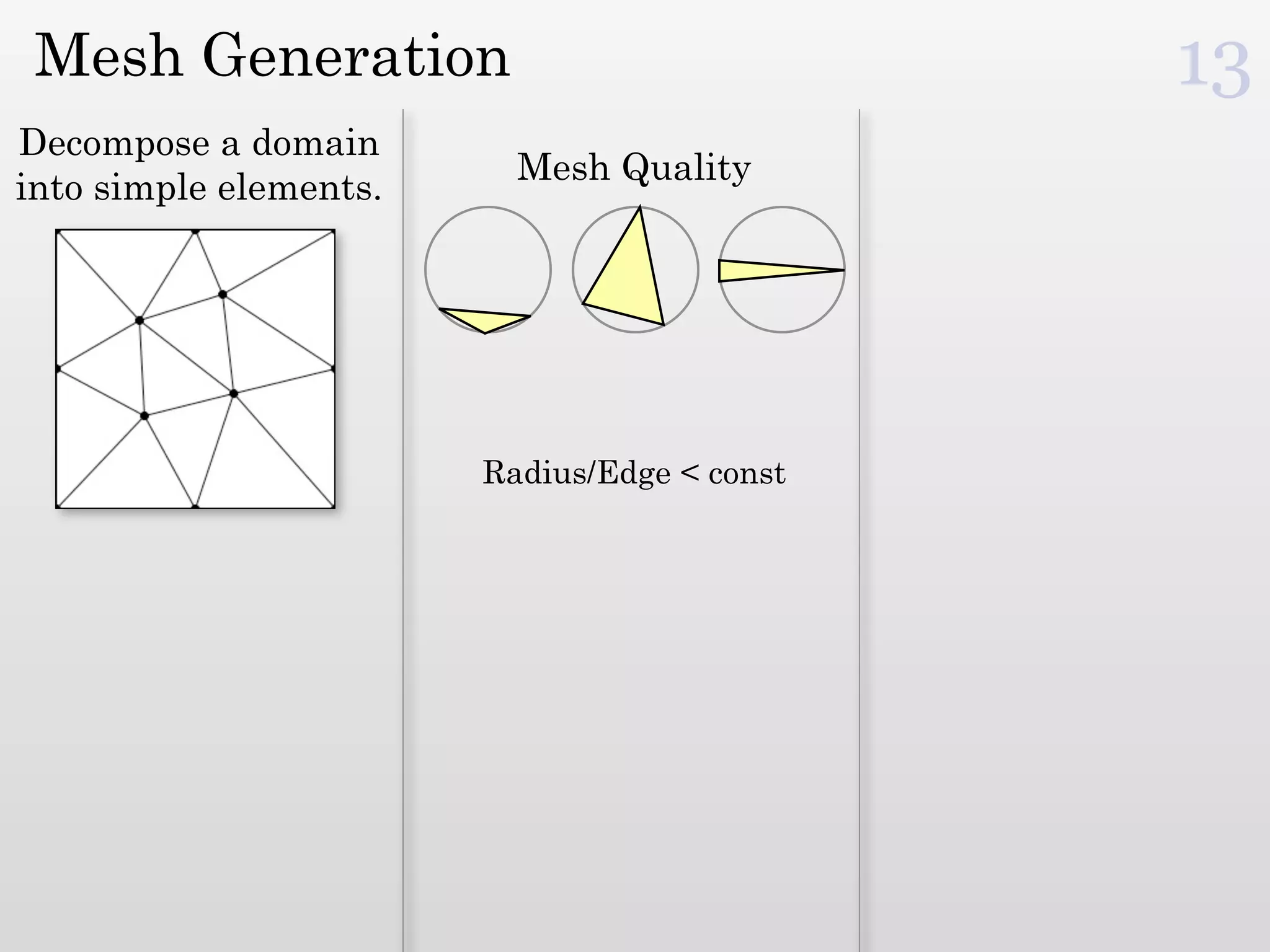
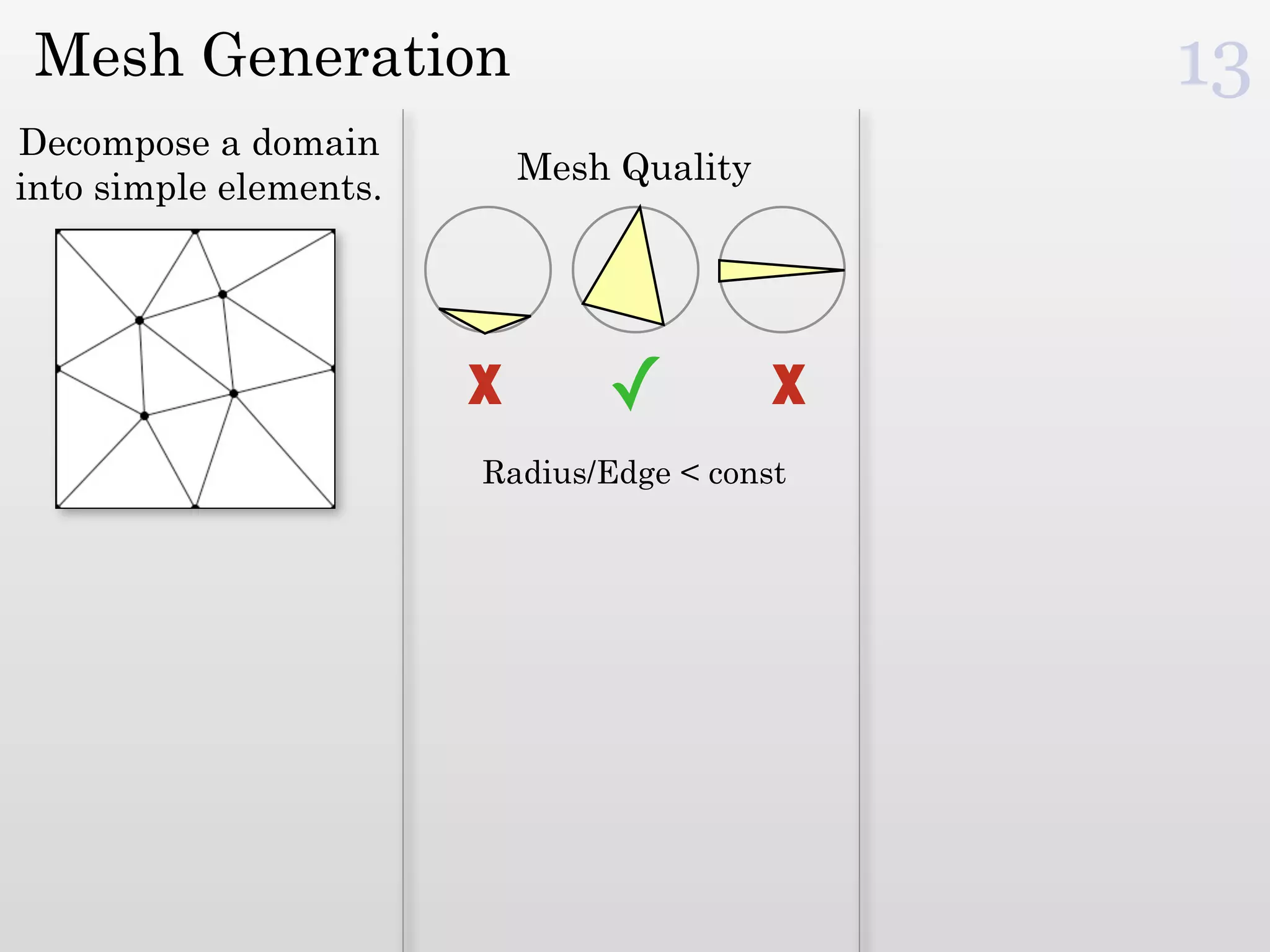
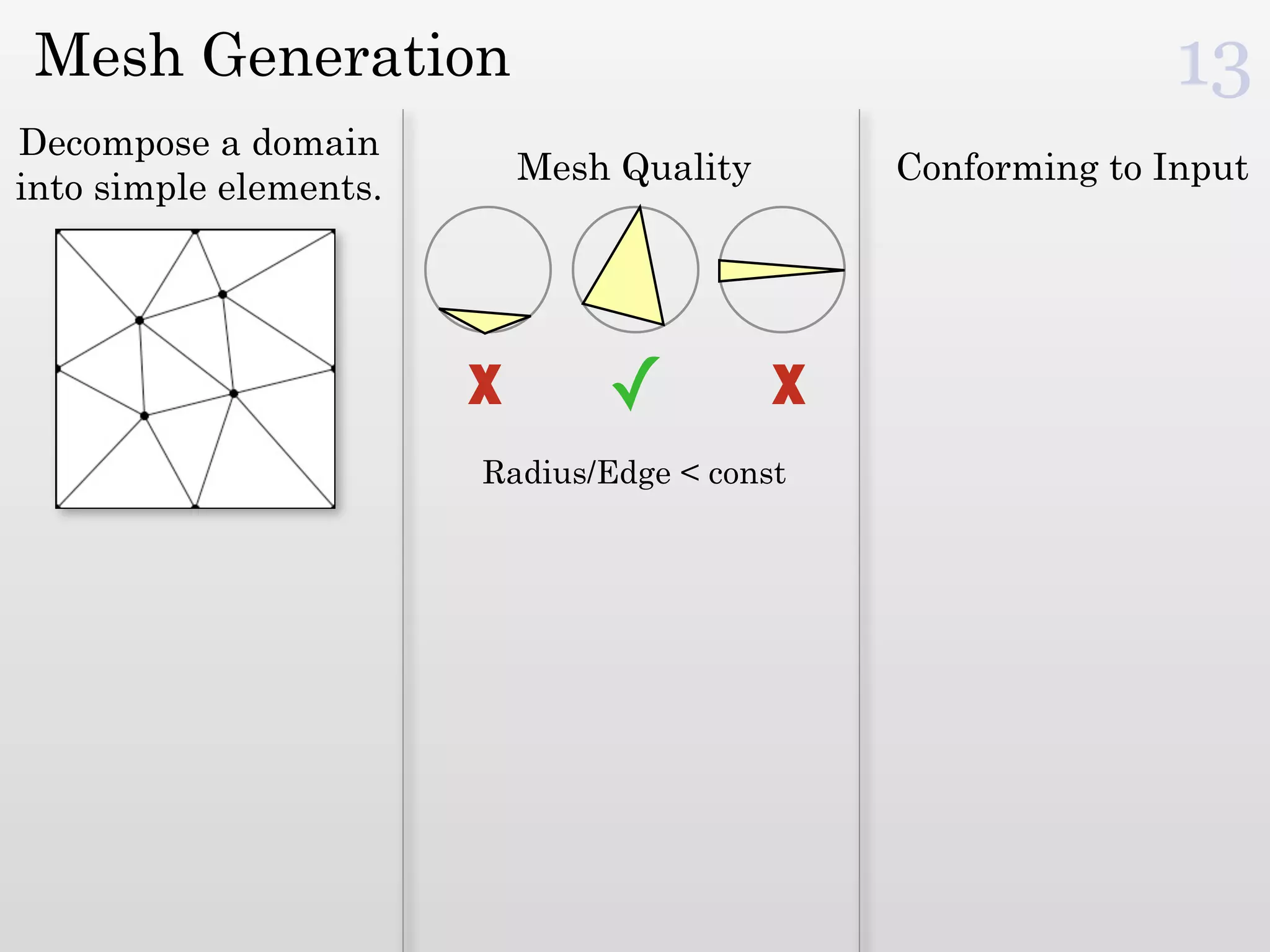
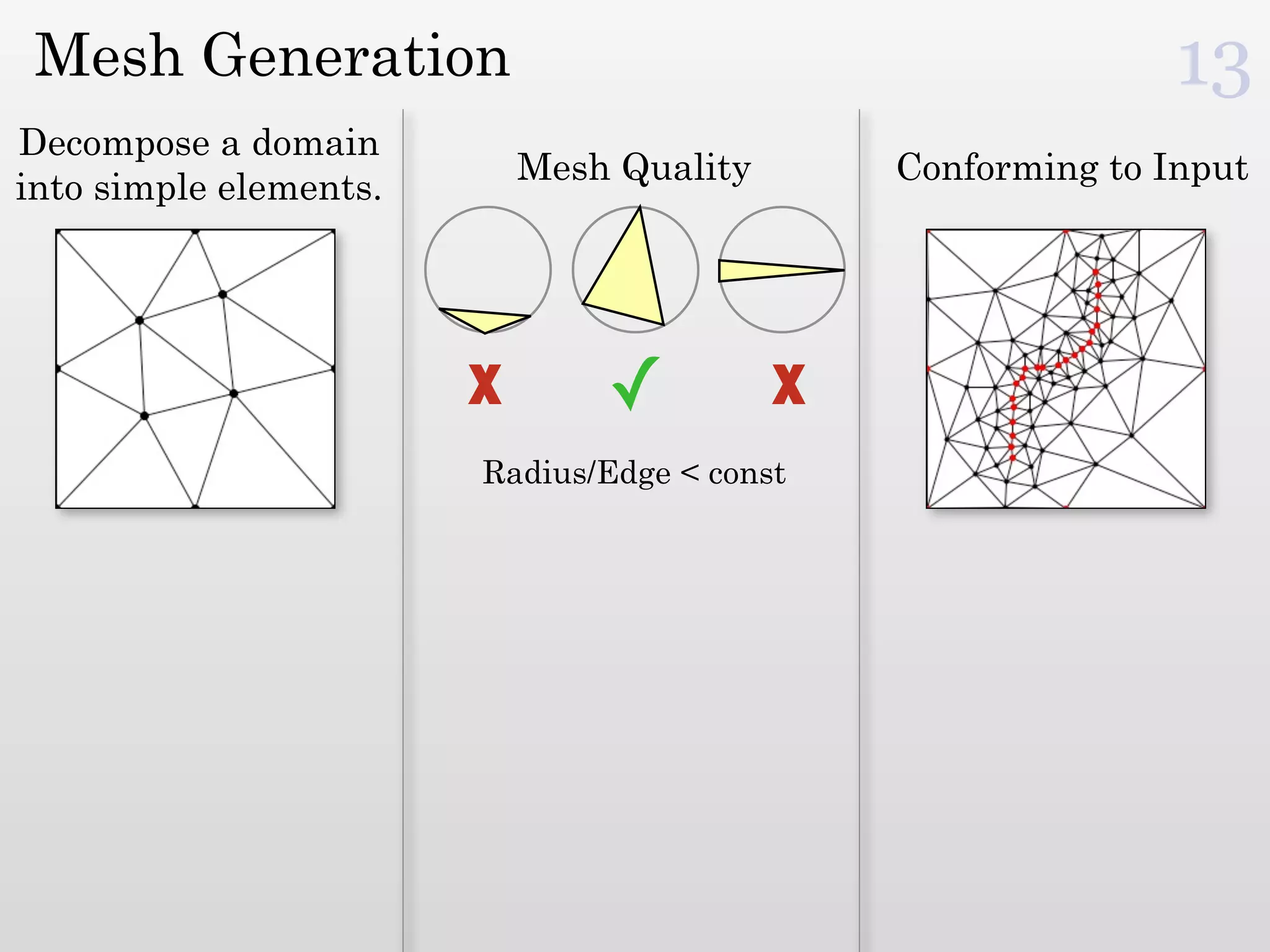
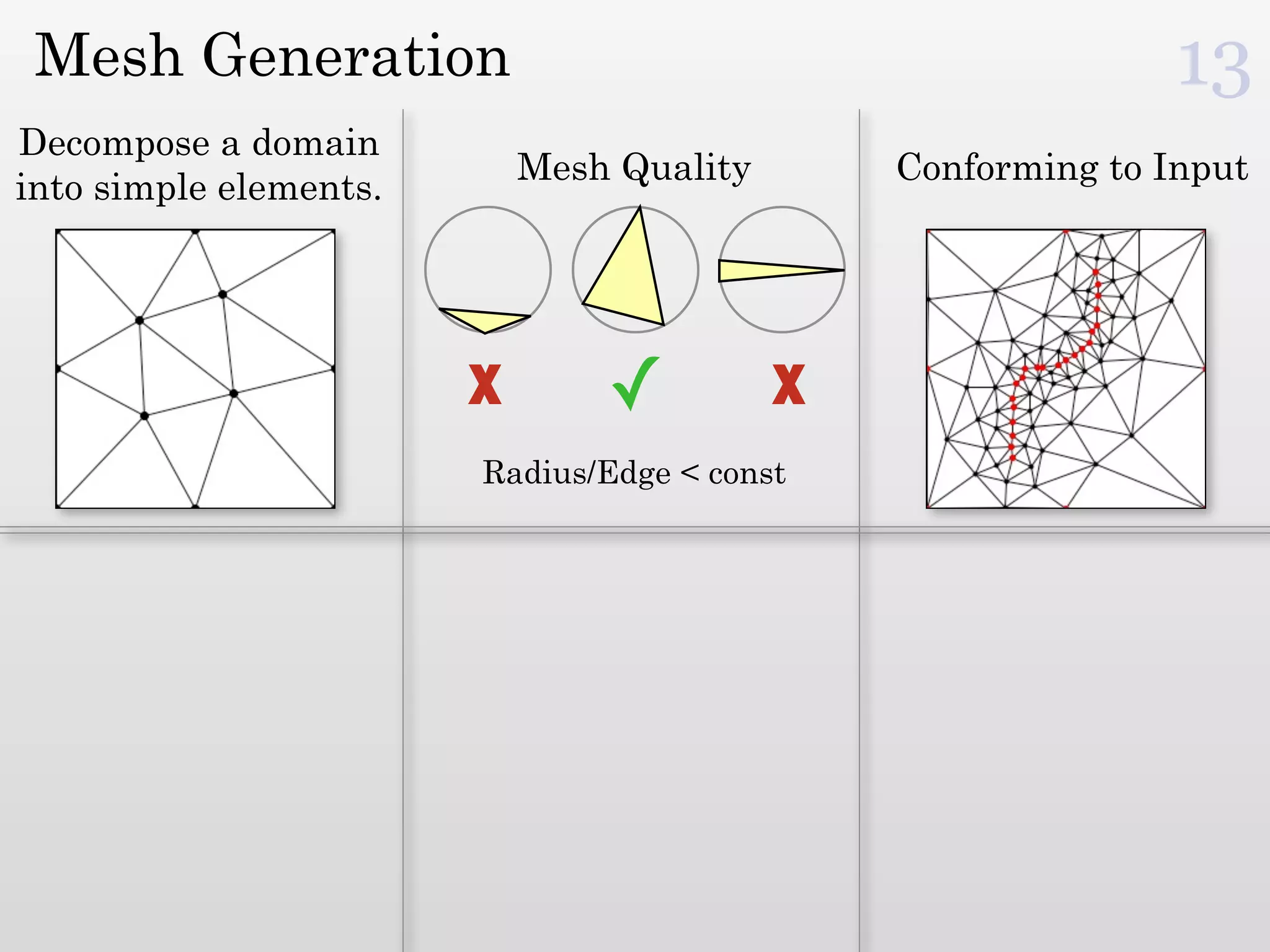
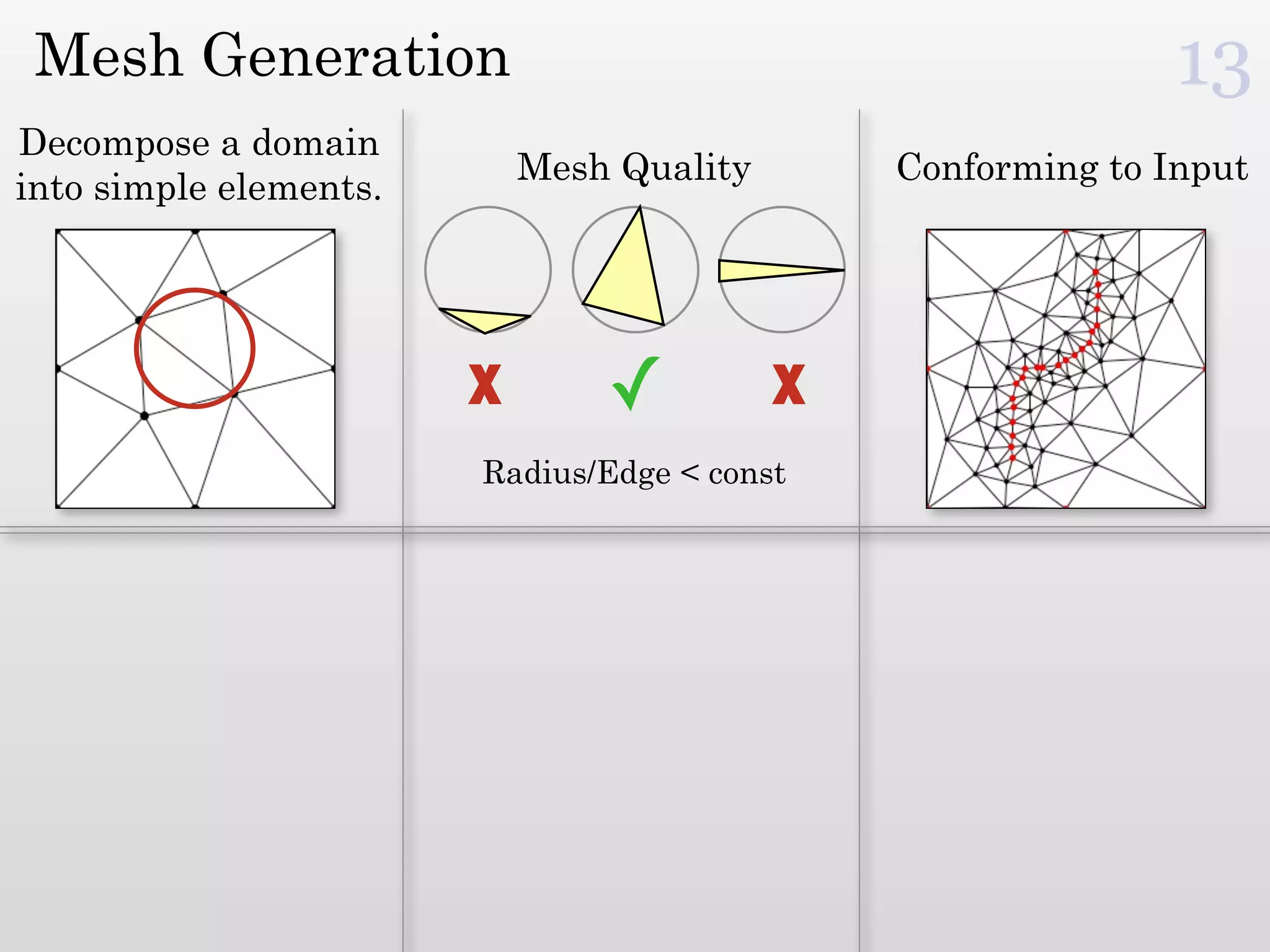
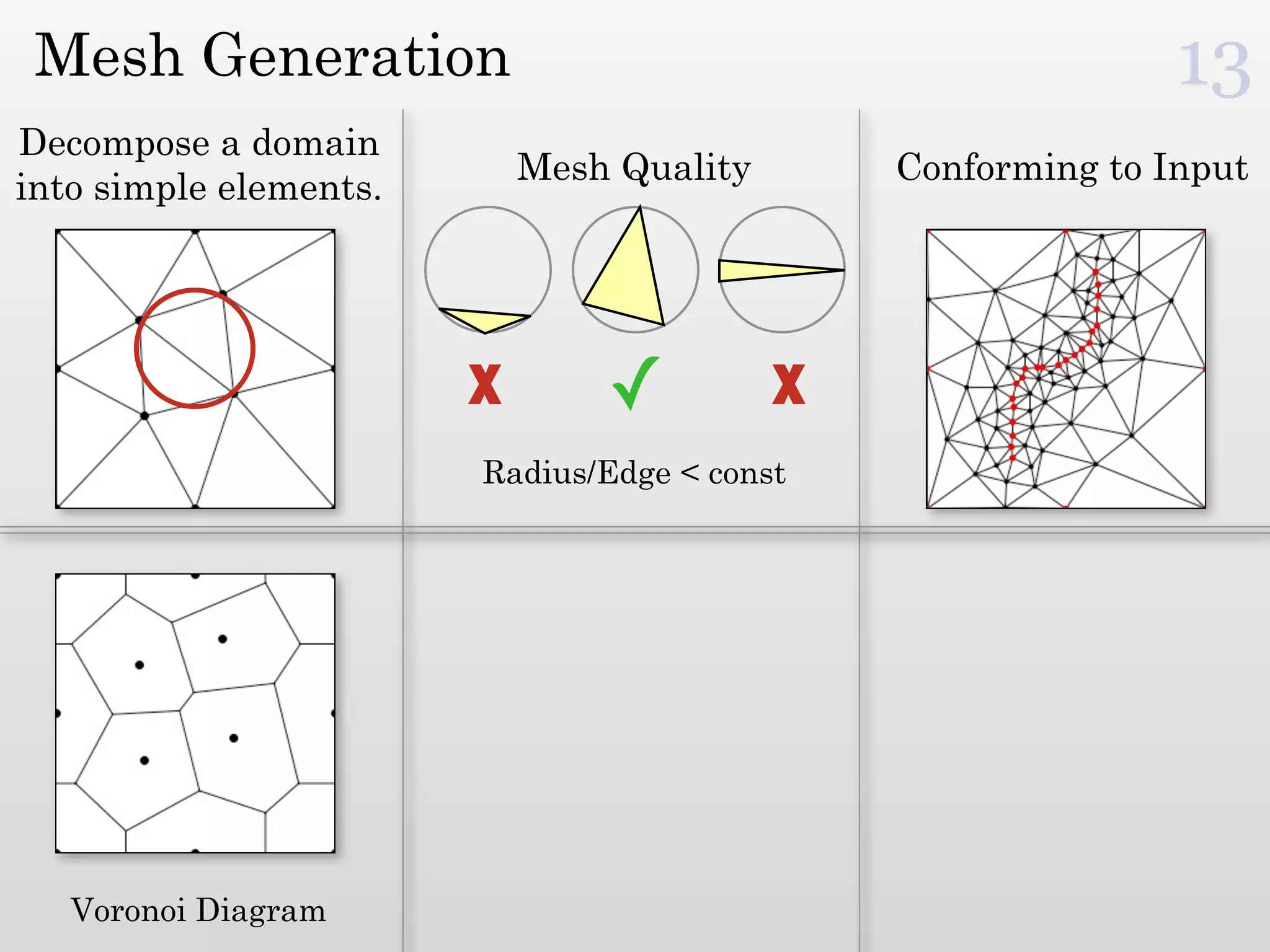
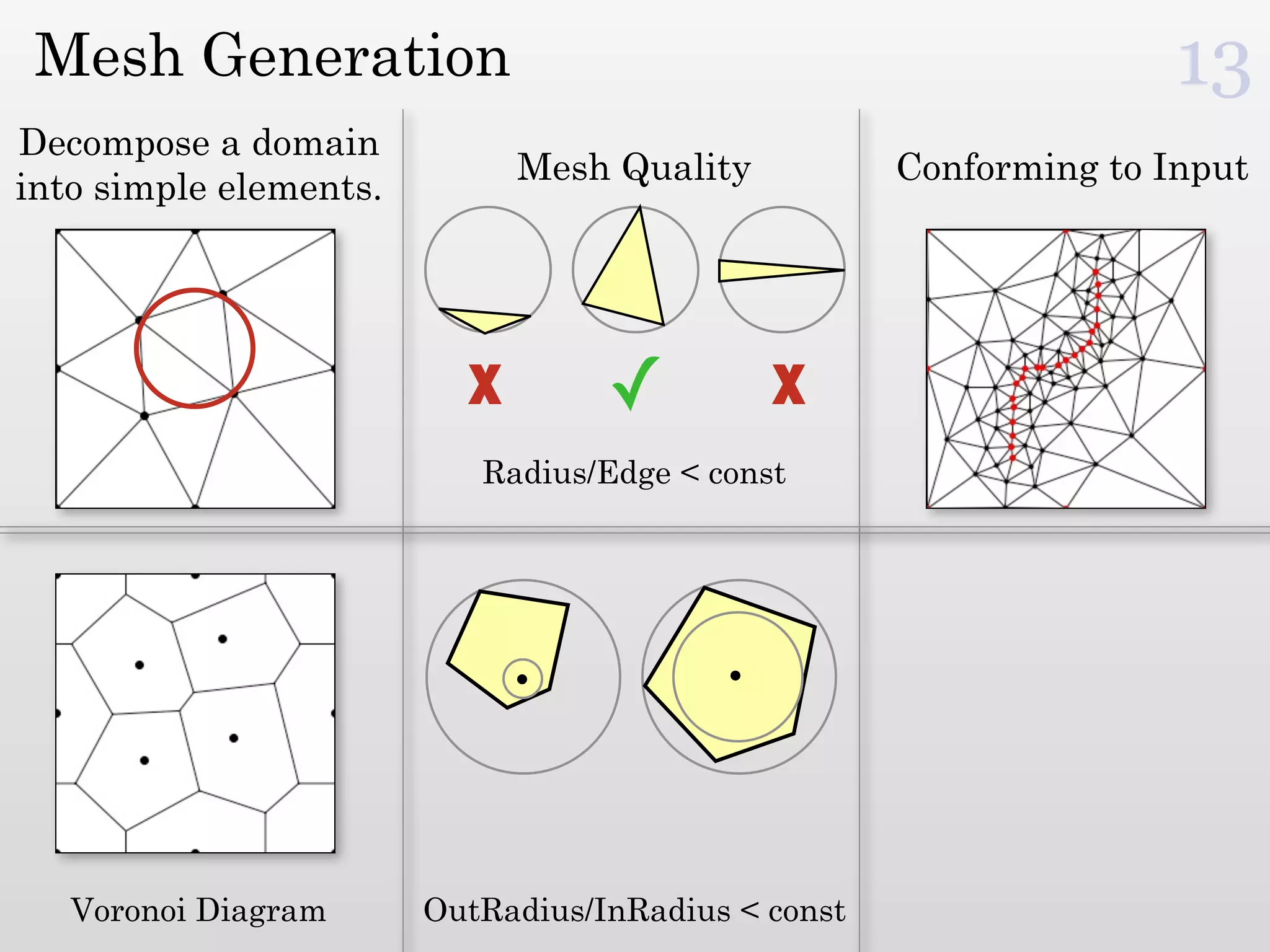
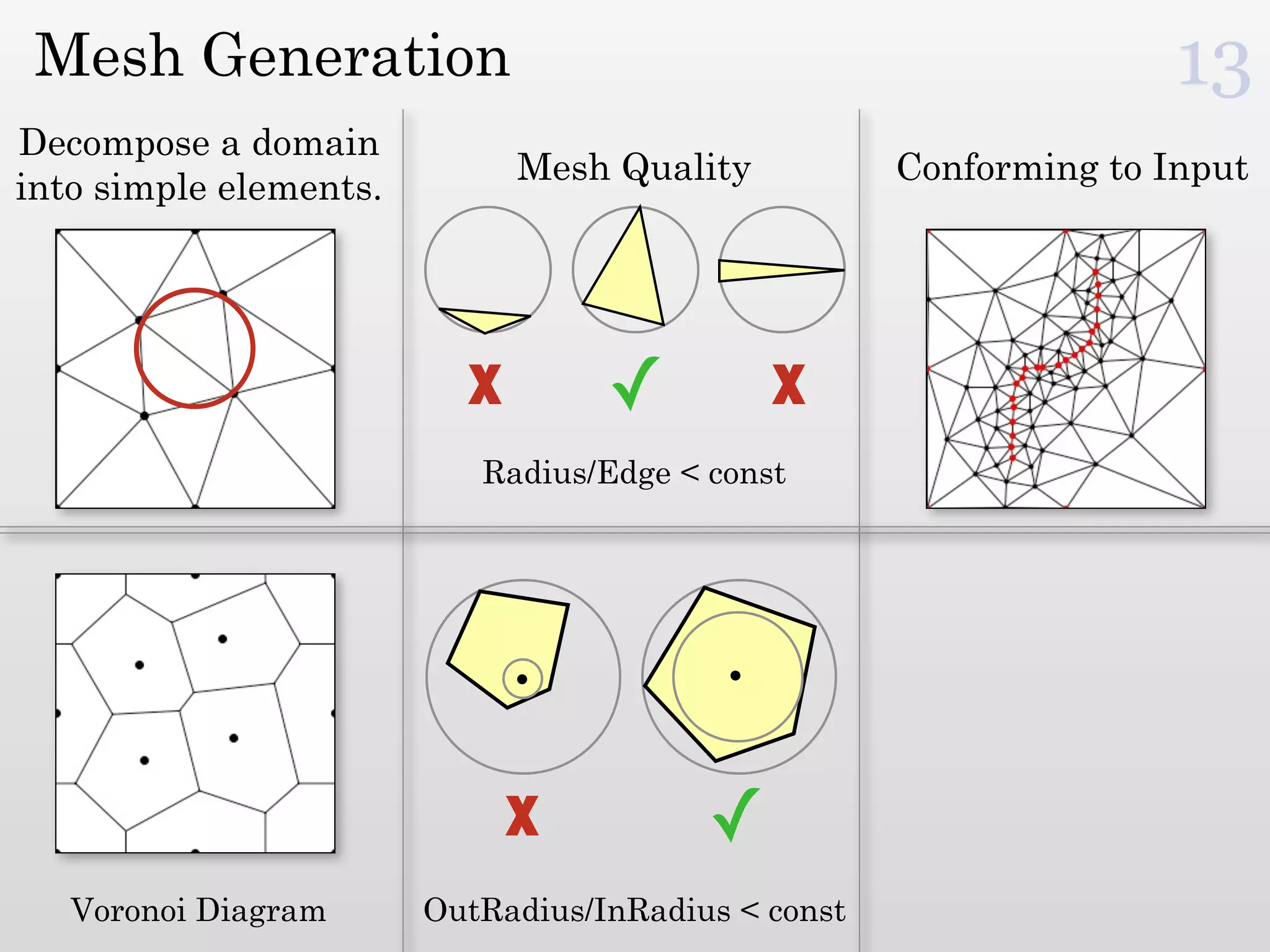
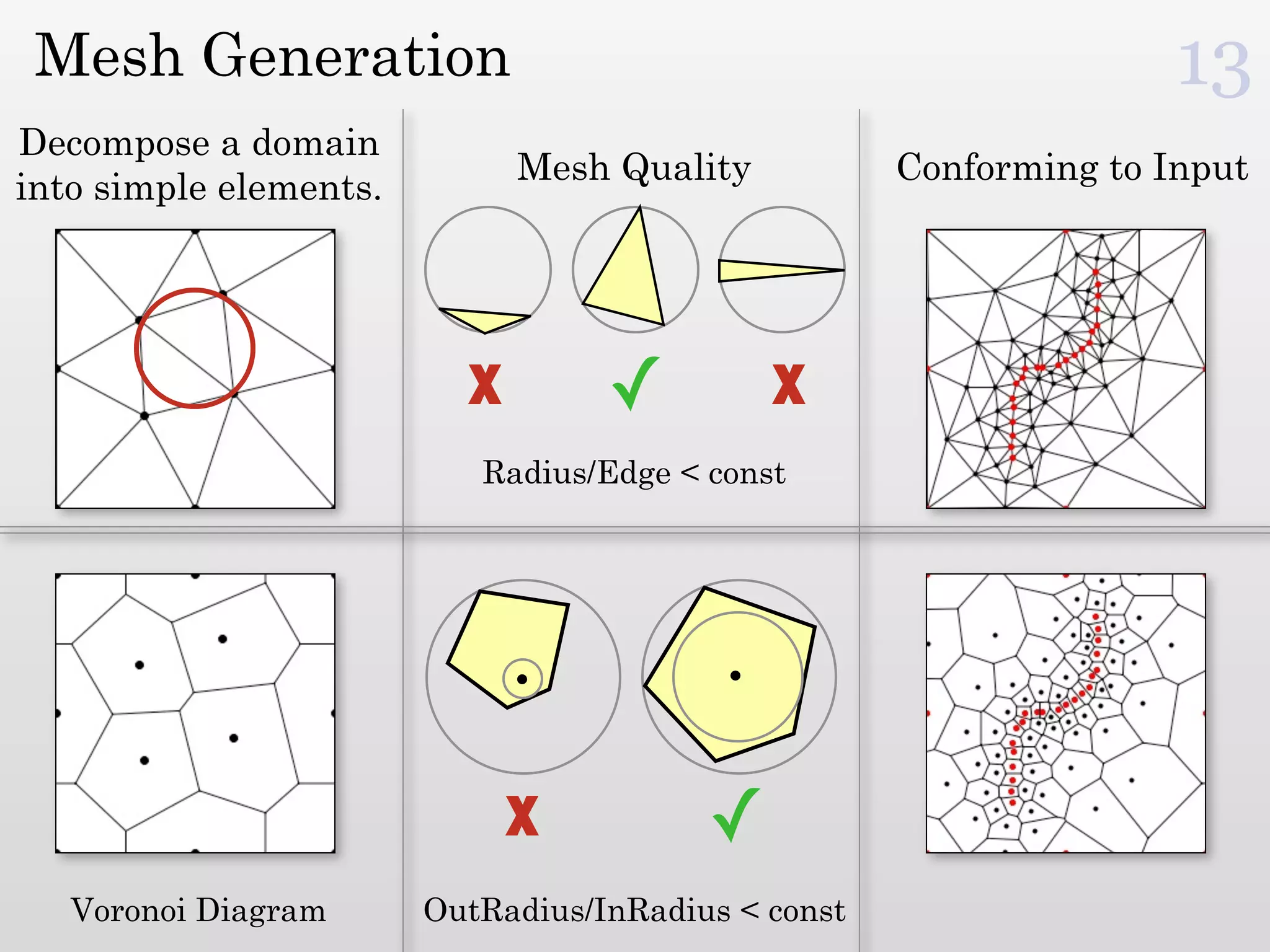
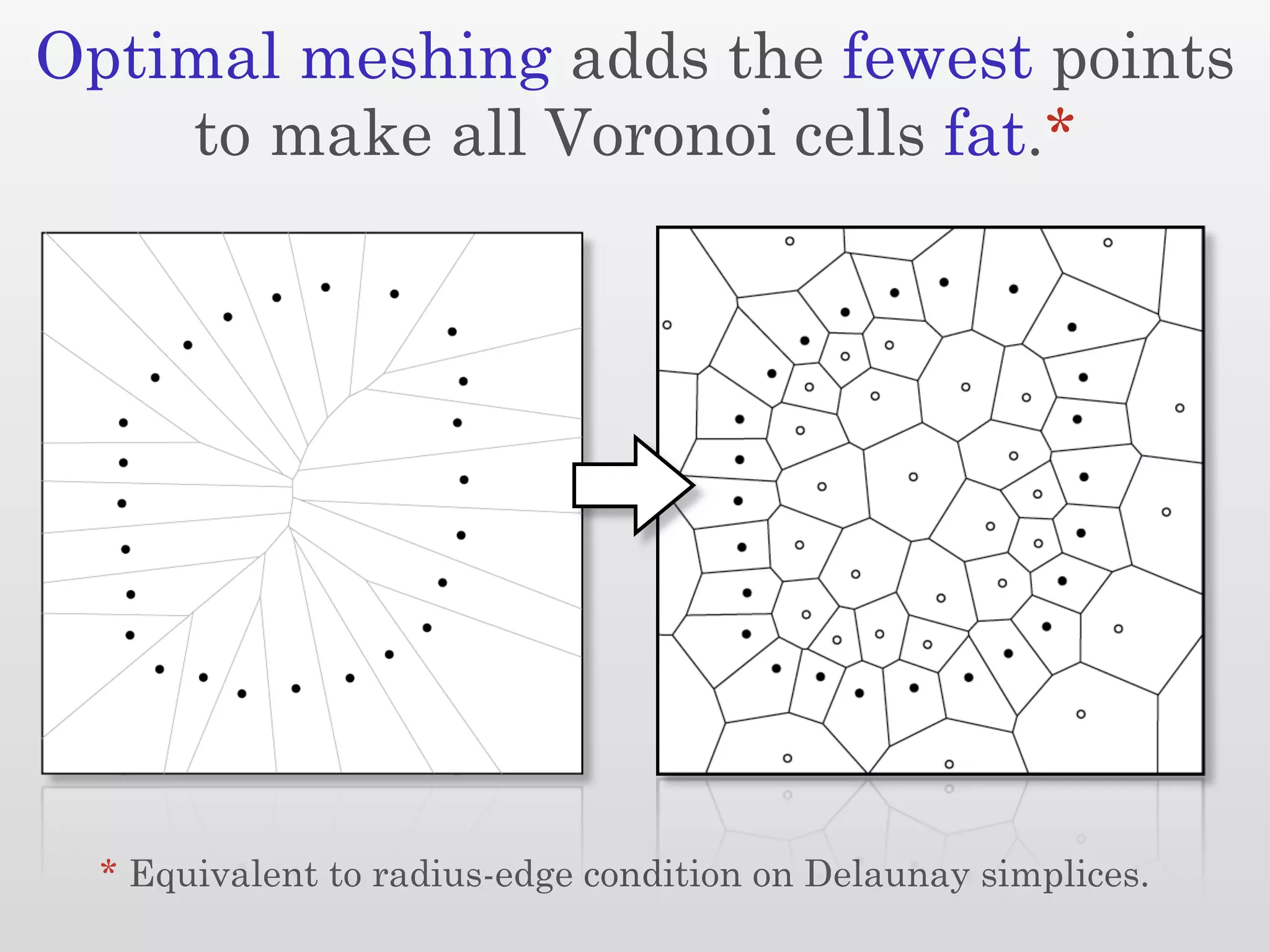
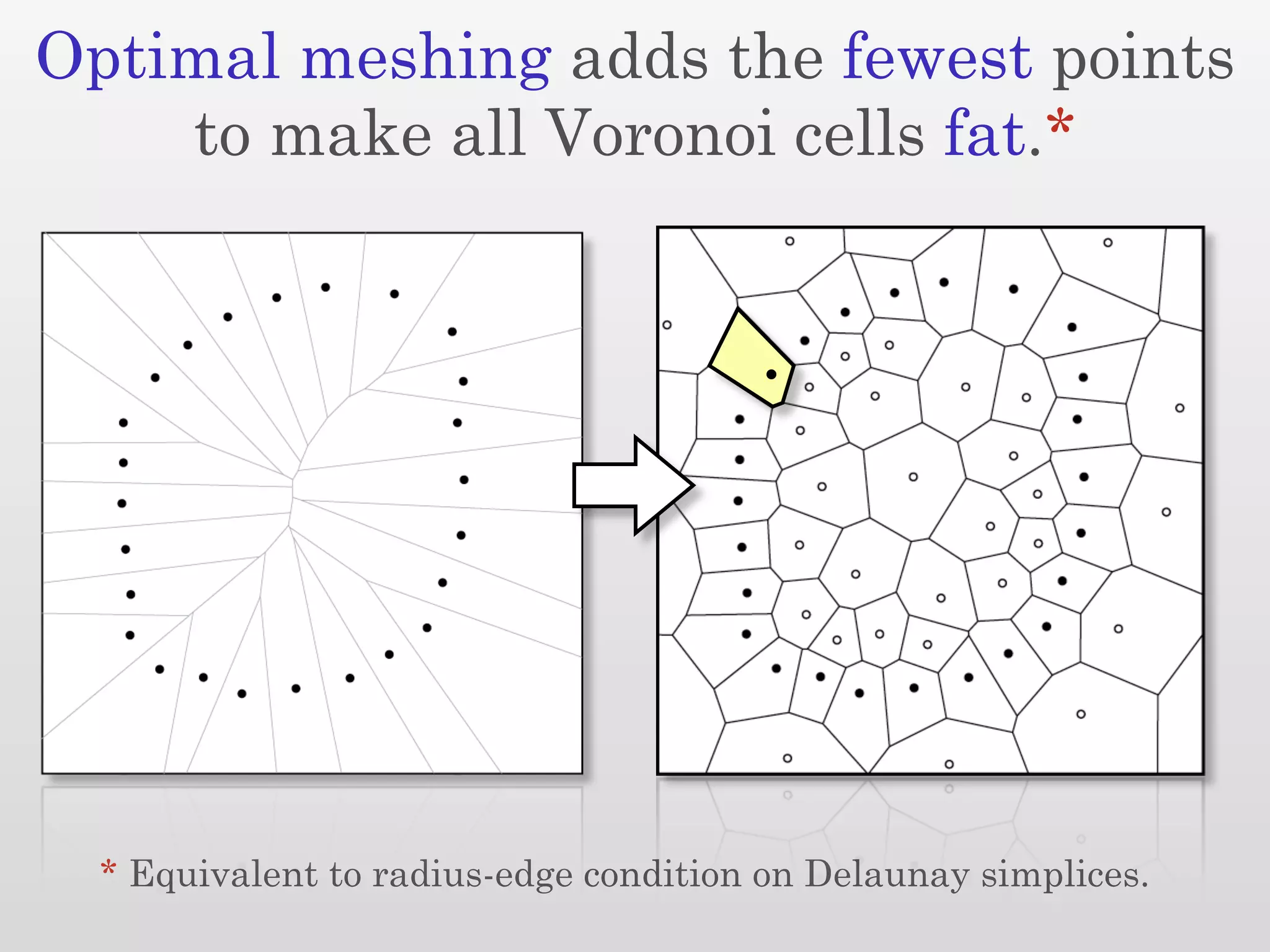
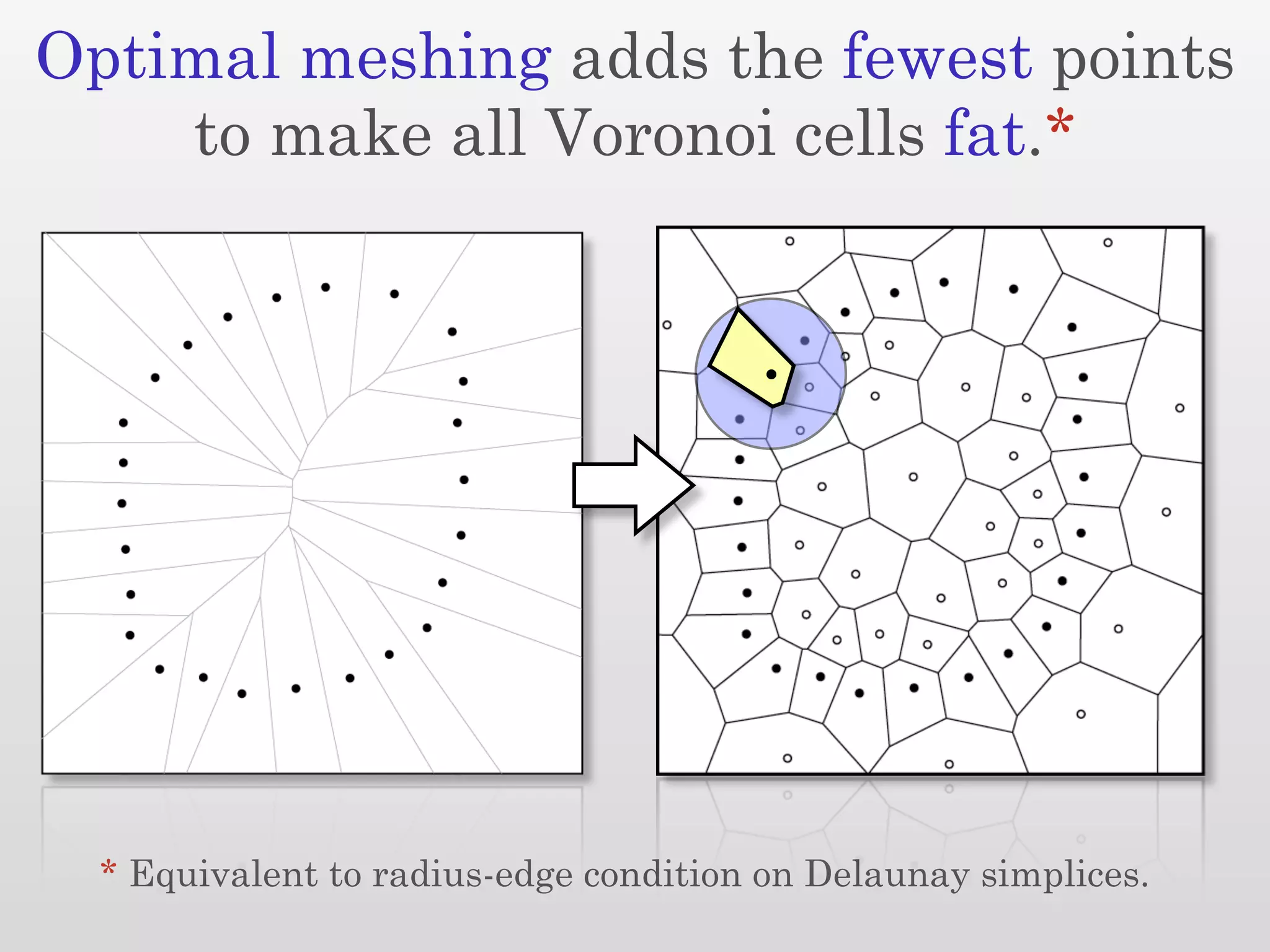
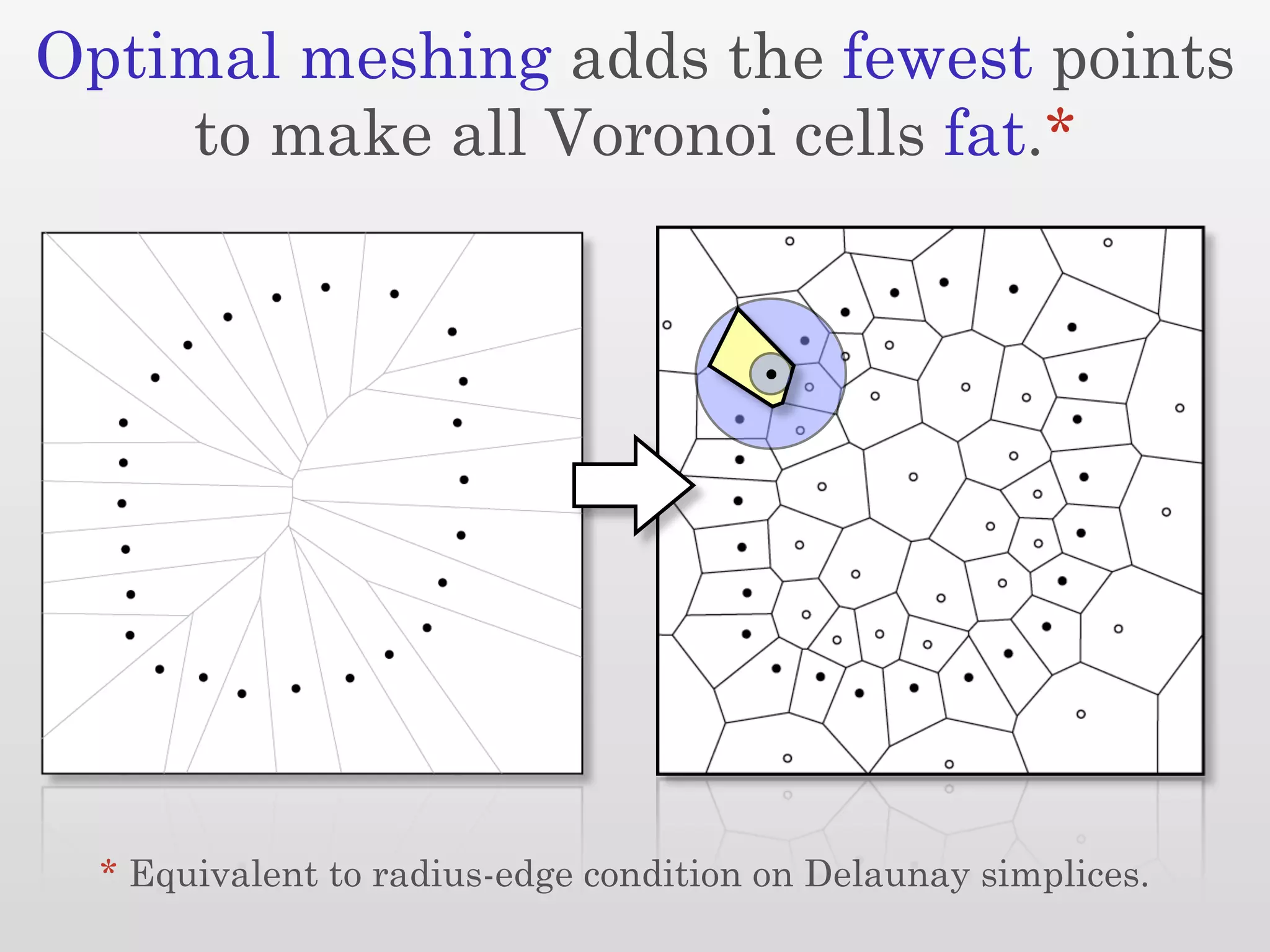
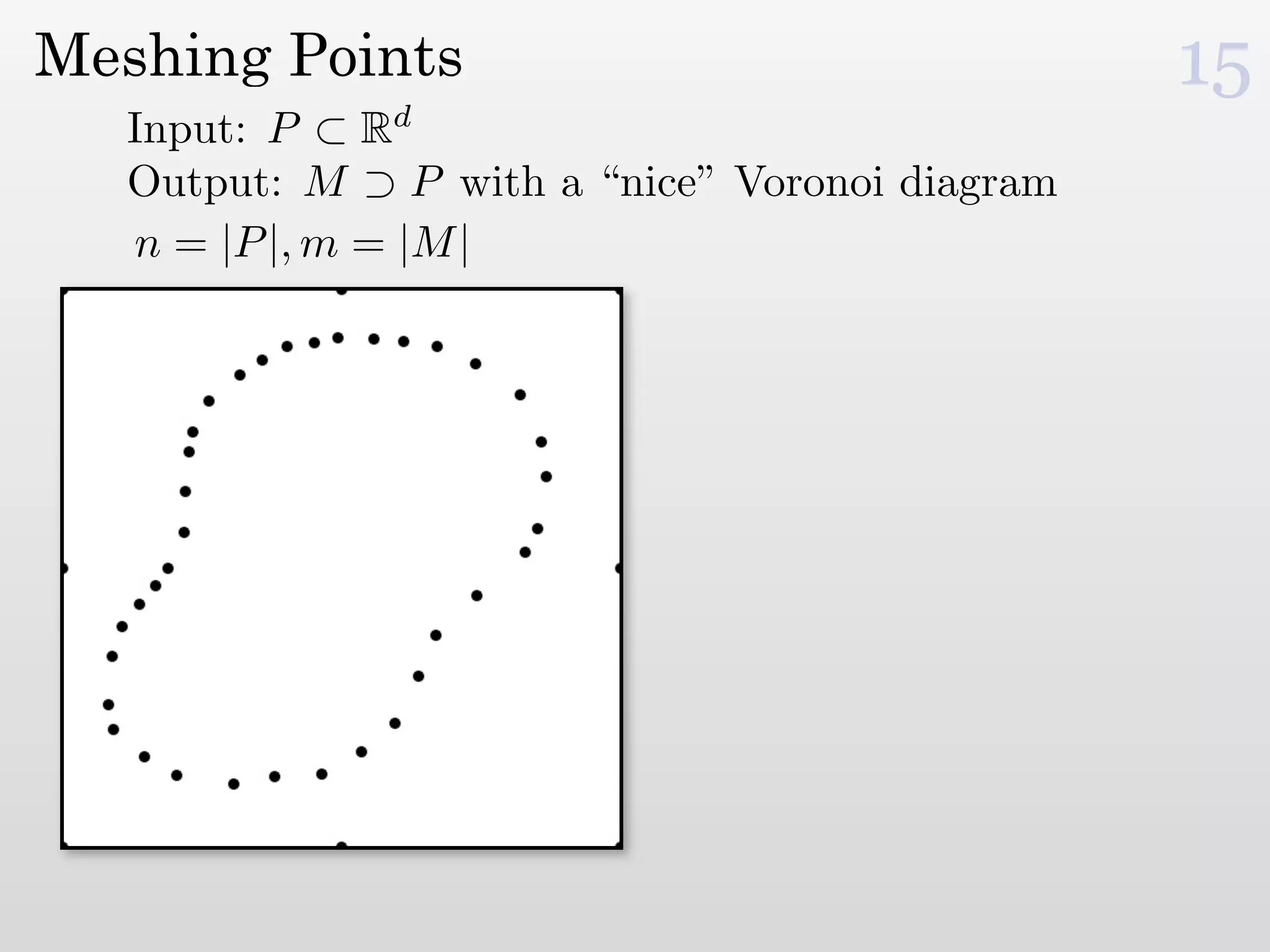
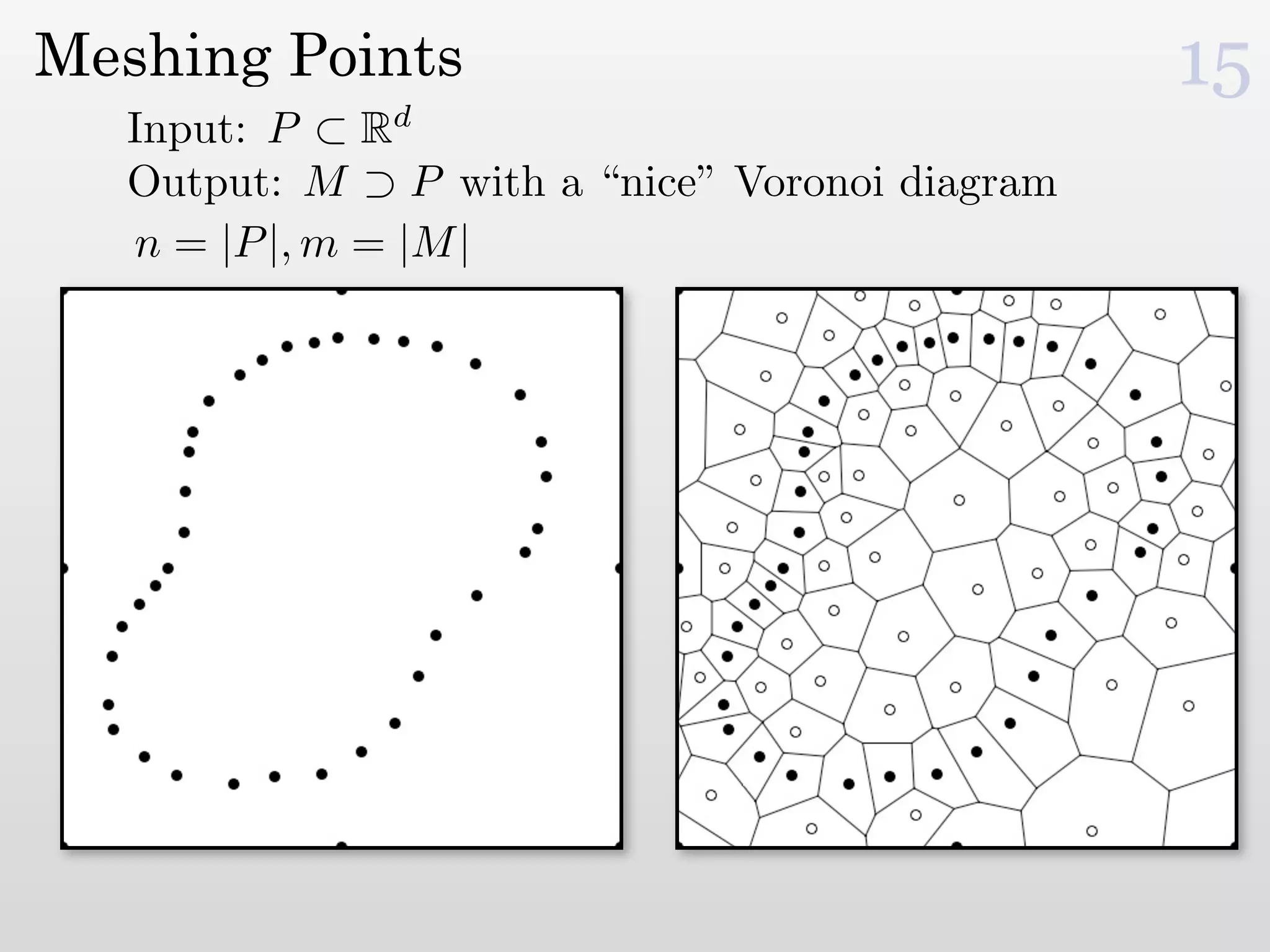
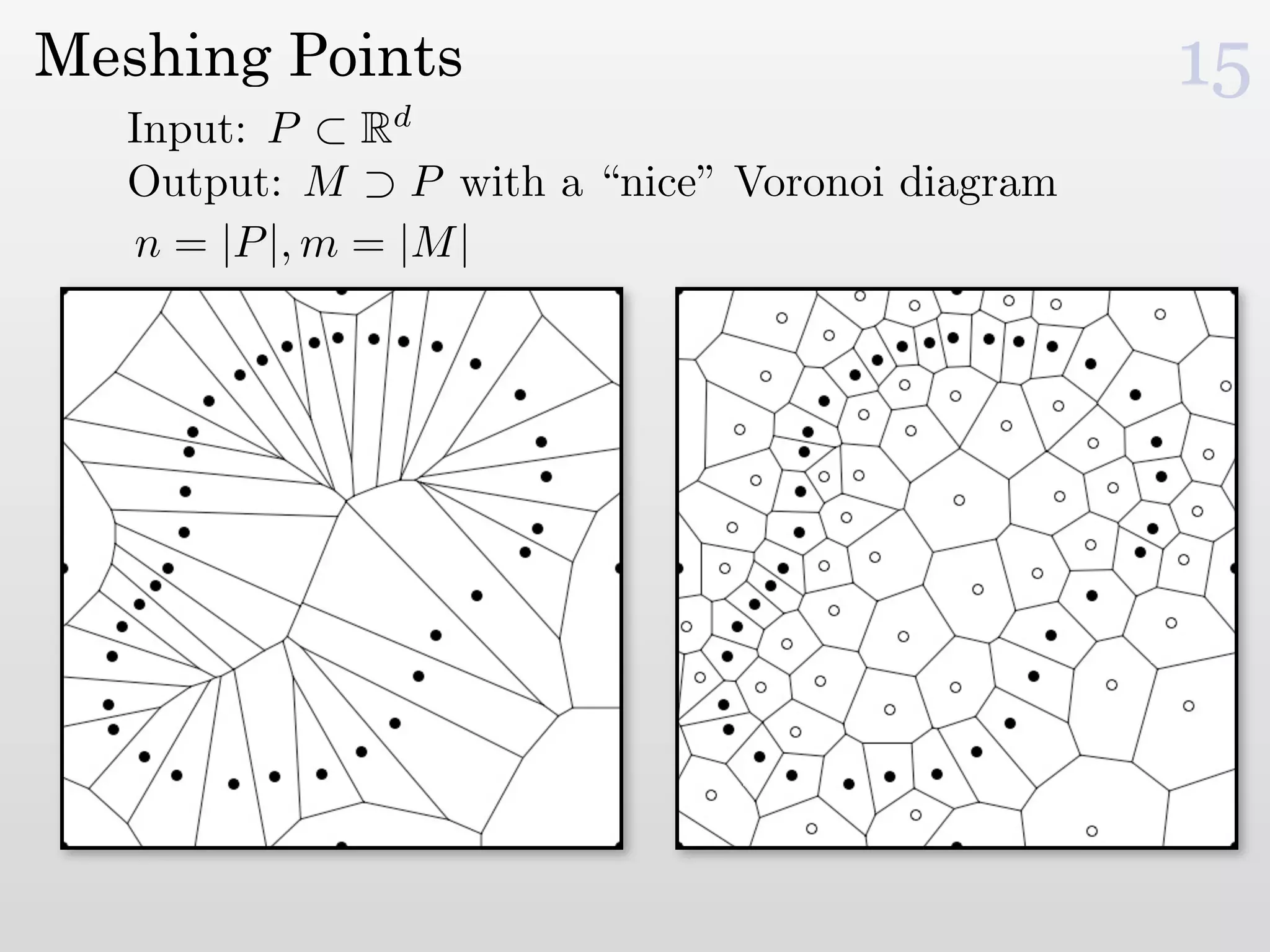
The document discusses mesh generation, which involves decomposing a domain into simple elements like triangles or tetrahedra. An optimal mesh has good element quality, conforms to the input domain, and uses the minimum number of points needed to make all Voronoi cells sufficiently "fat" or well-shaped according to metrics like radius-edge ratios. The talk presents analysis showing that the optimal mesh size is determined by the "feature size measure" of the input points, which involves the distance to each point's second nearest neighbor.

Embed presentation

Download to read offline
1 / 139
2 / 139
3 / 139
4 / 139
5 / 139
6 / 139
7 / 139
8 / 139
9 / 139
10 / 139
11 / 139
12 / 139
13 / 139
14 / 139
15 / 139
16 / 139
17 / 139
18 / 139
19 / 139
20 / 139
21 / 139
22 / 139
23 / 139
24 / 139
25 / 139
26 / 139
27 / 139
28 / 139
29 / 139
30 / 139
31 / 139
32 / 139
33 / 139
34 / 139
35 / 139
36 / 139
37 / 139
38 / 139
39 / 139
40 / 139
41 / 139
42 / 139
43 / 139
44 / 139
45 / 139
46 / 139
47 / 139
48 / 139
49 / 139
50 / 139
51 / 139
52 / 139
53 / 139
54 / 139
55 / 139
56 / 139
57 / 139
58 / 139
59 / 139
60 / 139
61 / 139
62 / 139
63 / 139
64 / 139
65 / 139
66 / 139
67 / 139
68 / 139
69 / 139
70 / 139
71 / 139
72 / 139
73 / 139
74 / 139
75 / 139
76 / 139
77 / 139
78 / 139
79 / 139
80 / 139
81 / 139
82 / 139
83 / 139
84 / 139
85 / 139
86 / 139
87 / 139
88 / 139
89 / 139
90 / 139
91 / 139
92 / 139
93 / 139
94 / 139
95 / 139
96 / 139
97 / 139
98 / 139
99 / 139
100 / 139
101 / 139
102 / 139
103 / 139
104 / 139
105 / 139
106 / 139
107 / 139
108 / 139
109 / 139
110 / 139
111 / 139
112 / 139
113 / 139
114 / 139
115 / 139
116 / 139
117 / 139
118 / 139
119 / 139
120 / 139
121 / 139
122 / 139
123 / 139
124 / 139
125 / 139
126 / 139
127 / 139
128 / 139
129 / 139
130 / 139
131 / 139
132 / 139
133 / 139
134 / 139
135 / 139
136 / 139
137 / 139
138 / 139
139 / 139
New Bounds on the Size of Optimal Meshes Don Sheehy Geometrica INRIA
Mesh Generation
Mesh Generation 1 Decompose a volume into simplices.
Mesh Generation 1 Decompose a volume into simplices. 2 Simplices should be quality.
Mesh Generation 1 Decompose a volume into simplices. 2 Simplices should be quality.
Mesh Generation 1 Decompose a volume into simplices. 2 Simplices should be quality. 3 Output should conform to input.
Mesh Generation 1 Decompose a volume into simplices. 2 Simplices should be quality. 3 Output should conform to input.
Mesh Generation
Mesh Generation Uses:
Mesh Generation Uses: PDEs via FEM
Mesh Generation Uses: PDEs via FEM Data Analysis
Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes:
Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle
Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL
Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL TetGen
Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL TetGen Theoretical Guarantees:
Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL TetGen Theoretical Guarantees: Sliver Removal
Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL TetGen Theoretical Guarantees: Sliver Removal Surface Reconstruction
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms
Local Refinement Algorithms Pros:
Local Refinement Algorithms Pros: Easy to implement
Local Refinement Algorithms Pros: Easy to implement Often Parallel
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons:
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination?
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations?
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations?
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations?
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations? How many points?
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations? How many points?
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Yes. Accumulations? How many points?
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Yes. Accumulations? No. How many points?
Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Yes. Accumulations? No. How many points? This is what we’ll answer.
The size of an optimal mesh is given by the feature size measure.
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P .
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P .
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P .
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . x
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . s( x) x lf
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . x
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . x lfs( x)
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . dx Optimal Mesh Size = Θ Ω lfs(x)d x lfs( x)
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . number of vertices dx Optimal Mesh Size = Θ Ω lfs(x)d x lfs( x)
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . number of vertices dx Optimal Mesh Size = Θ Ω lfs(x)d hides simple exponential in d x lfs( x)
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . number of vertices dx Optimal Mesh Size = Θ Ω lfs(x)d hides simple exponential in d dx The Feature Size Measure: µP (Ω) = lfsP (x)d Ω x lfs( x)
The size of an optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . number of vertices dx Optimal Mesh Size = Θ Ω lfs(x)d hides simple exponential in d dx The Feature Size Measure: µP (Ω) = lfsP (x)d Ω When is µP (Ω) = O(n)?
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
A canonical bad case for meshing is two points in a big empty space.
The feature size measure can be bounded in terms of the pacing.
The feature size measure can be bounded in terms of the pacing. Order the points.
The feature size measure can be bounded in terms of the pacing. Order the points.
The feature size measure can be bounded in terms of the pacing. Order the points.
The feature size measure can be bounded in terms of the pacing. Order the points.
The feature size measure can be bounded in terms of the pacing. Order the points.
The feature size measure can be bounded in terms of the pacing. Order the points.
The feature size measure can be bounded in terms of the pacing. pi Order the points.
The feature size measure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi )
The feature size measure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi ) b = pi − 2NN(pi )
The feature size measure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi ) b = pi − 2NN(pi ) b The pacing of the ith point is φi = a .
The feature size measure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi ) b = pi − 2NN(pi ) b The pacing of the ith point is φi = a . Let φ be the geometric mean, so log φi = n log φ.
The feature size measure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi ) b = pi − 2NN(pi ) b The pacing of the ith point is φi = a . Let φ be the geometric mean, so log φi = n log φ. φ is the pacing of the ordering.
The trick is to write the feature size measure as a telescoping sum.
The trick is to write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi }
The trick is to write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3
The trick is to write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point.
The trick is to write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point. µPi (Ω) − µPi−1 (Ω) = Θ(1 + log φi )
The trick is to write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point. µPi (Ω) − µPi−1 (Ω) = Θ(1 + log φi ) n log φi = n log φ i=3
The trick is to write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point. µPi (Ω) − µPi−1 (Ω) = Θ(1 + log φi ) n log φi = n log φ Θ(n + n log φ) i=3
The trick is to write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point. µPi (Ω) − µPi−1 (Ω) = Θ(1 + log φi ) n log φi = n log φ Θ(n + n log φ) i=3 d Previous bound: O(n + φ n).
Pacing analysis has already led to new results.
Pacing analysis has already led to new results. The Scaffold Theorem (SODA 2009) Given n points well-spaced on a surface, the volume mesh has size O(n).
Pacing analysis has already led to new results. The Scaffold Theorem (SODA 2009) Given n points well-spaced on a surface, the volume mesh has size O(n). Time-Optimal Point Meshing (SoCG 2011) Build a mesh in O(n log n + m) time. Algorithm explicitly computes the pacing for each insertion.
Some takeaway messages:
Some takeaway messages: 1 The amortized change in the number of vertices in a mesh as a result of adding one new point is determined by the pacing of that point.
Some takeaway messages: 1 The amortized change in the number of vertices in a mesh as a result of adding one new point is determined by the pacing of that point. 2 Point sets that admit linear size meshes are exactly those with constant pacing.
Some takeaway messages: 1 The amortized change in the number of vertices in a mesh as a result of adding one new point is determined by the pacing of that point. 2 Point sets that admit linear size meshes are exactly those with constant pacing. Thank you.
Mesh Generation 13
Mesh Generation 13 Decompose a domain into simple elements.
Mesh Generation 13 Decompose a domain into simple elements.
Mesh Generation 13 Decompose a domain Mesh Quality into simple elements. Radius/Edge < const
Mesh Generation 13 Decompose a domain Mesh Quality into simple elements. X ✓ X Radius/Edge < const
Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const
Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const
Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const
Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const
Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const Voronoi Diagram
Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const Voronoi Diagram OutRadius/InRadius < const
Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const X ✓ Voronoi Diagram OutRadius/InRadius < const
Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const X ✓ Voronoi Diagram OutRadius/InRadius < const
Optimal meshing adds the fewest points to make all Voronoi cells fat.* * Equivalent to radius-edge condition on Delaunay simplices.
Optimal meshing adds the fewest points to make all Voronoi cells fat.* * Equivalent to radius-edge condition on Delaunay simplices.
Optimal meshing adds the fewest points to make all Voronoi cells fat.* * Equivalent to radius-edge condition on Delaunay simplices.
Optimal meshing adds the fewest points to make all Voronoi cells fat.* * Equivalent to radius-edge condition on Delaunay simplices.
Meshing Points 15 Input: P ⊂ Rd Output: M ⊃ P with a “nice” Voronoi diagram n = |P |, m = |M |
Meshing Points 15 Input: P ⊂ Rd Output: M ⊃ P with a “nice” Voronoi diagram n = |P |, m = |M |
Meshing Points 15 Input: P ⊂ Rd Output: M ⊃ P with a “nice” Voronoi diagram n = |P |, m = |M |
Meshing Points 15 Input: P ⊂ Rd Output: M ⊃ P with a “nice” Voronoi diagram n = |P |, m = |M |
How to prove a meshing algorithm is optimal.16
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P x
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P x fP (x)
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P x
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P ( x) x fP
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d “No 2 points too close together” “Optimal Size Output”
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d “No 2 points too close together” “Optimal Size Output” v
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d “No 2 points too close together” “Optimal Size Output” v fM (v)
How to prove a meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d “No 2 points too close together” “Optimal Size Output” v ( v) fM (v) fP

More Related Content

PDF
Fourier Transforms
byArvind Devaraj
 
PDF
t-vMF Similarity
byKyushu University
 
PDF
Introduction to compressive sensing
byAhmed Nasser Agag
 
PDF
Optimal Meshing
byDon Sheehy
 
KEY
Team meeting 100325
byYi-Hsin Liu
 
PPTX
CPM2013-tabei201306
byYasuo Tabei
 
PPT
Thesis : &quot;IBBET : In Band Bandwidth Estimation for LAN&quot;
byVishalkumarec
 
PDF
Cb25464467
byIJERA Editor
 
Fourier Transforms
byArvind Devaraj
 
t-vMF Similarity
byKyushu University
 
Introduction to compressive sensing
byAhmed Nasser Agag
 
Optimal Meshing
byDon Sheehy
 
Team meeting 100325
byYi-Hsin Liu
 
CPM2013-tabei201306
byYasuo Tabei
 
Thesis : &quot;IBBET : In Band Bandwidth Estimation for LAN&quot;
byVishalkumarec
 
Cb25464467
byIJERA Editor
 

What's hot

PDF
Statistical Analysis of Neural Coding
byYifei Shea, Ph.D.
 
PDF
Maximizing Submodular Function over the Integer Lattice
byTasuku Soma
 
PDF
2013-1 Machine Learning Lecture 02 - Andrew Moore: Entropy
byDongseo University
 
PDF
Python faster for loop
by💾 Radek Fabisiak
 
PDF
FK_icassp_2014
byFangchen FENG
 
PPTX
DCC2014 - Fully Online Grammar Compression in Constant Space
byYasuo Tabei
 
PDF
Seven waystouseturtle pycon2009
byA Jorge Garcia
 
PPT
Single Sample Soft Shadows Using Depth Maps
bystefan_b
 
PDF
Effective Numerical Computation in NumPy and SciPy
byKimikazu Kato
 
PDF
機械学習によるデータ分析 実践編
byRyota Kamoshida
 
PPT
Chapter 5 Image Processing: Fourier Transformation
byVarun Ojha
 
PPTX
584 fundamental theorem of calculus
bygoldenratio618
 
PDF
Masters Report 3
byLloyd Blackbeard
 
PDF
Art%3 a10.1155%2fs1110865704401036
bySANDRA BALSECA
 
PDF
Ning_Mei.ASSIGN02
by宁 梅
 
DOC
Fuzzieee-98-final
bySumit Sen
 
PDF
Radio ad blocker
byTomasz Rękawek
 
ZIP
Mas college5 2011.key
byeosinophil_g
 
PDF
A Physical Approach to Moving Cast Shadow Detection (ICASSP 2009)
byJia-Bin Huang
 
PDF
Unexpected Default in an Information based model
byMatteo Bedini
 
Statistical Analysis of Neural Coding
byYifei Shea, Ph.D.
 
Maximizing Submodular Function over the Integer Lattice
byTasuku Soma
 
2013-1 Machine Learning Lecture 02 - Andrew Moore: Entropy
byDongseo University
 
Python faster for loop
by💾 Radek Fabisiak
 
FK_icassp_2014
byFangchen FENG
 
DCC2014 - Fully Online Grammar Compression in Constant Space
byYasuo Tabei
 
Seven waystouseturtle pycon2009
byA Jorge Garcia
 
Single Sample Soft Shadows Using Depth Maps
bystefan_b
 
Effective Numerical Computation in NumPy and SciPy
byKimikazu Kato
 
機械学習によるデータ分析 実践編
byRyota Kamoshida
 
Chapter 5 Image Processing: Fourier Transformation
byVarun Ojha
 
584 fundamental theorem of calculus
bygoldenratio618
 
Masters Report 3
byLloyd Blackbeard
 
Art%3 a10.1155%2fs1110865704401036
bySANDRA BALSECA
 
Ning_Mei.ASSIGN02
by宁 梅
 
Fuzzieee-98-final
bySumit Sen
 
Radio ad blocker
byTomasz Rękawek
 
Mas college5 2011.key
byeosinophil_g
 
A Physical Approach to Moving Cast Shadow Detection (ICASSP 2009)
byJia-Bin Huang
 
Unexpected Default in an Information based model
byMatteo Bedini
 

Viewers also liked

PDF
On Nets and Meshes
byDon Sheehy
 
PDF
Linear Size Meshes
byDon Sheehy
 
PDF
Mesh Generation and Topological Data Analysis
byDon Sheehy
 
PDF
Linear-Size Approximations to the Vietoris-Rips Filtration - Presented at Uni...
byDon Sheehy
 
PDF
Characterizing the Distortion of Some Simple Euclidean Embeddings
byDon Sheehy
 
PDF
ATMCS: Linear-Size Approximations to the Vietoris-Rips Filtration
byDon Sheehy
 
PDF
Output-Sensitive Voronoi Diagrams and Delaunay Triangulations
byDon Sheehy
 
PDF
Ball Packings and Fat Voronoi Diagrams
byDon Sheehy
 
PPT
Overlay Stitch Meshing
byDon Sheehy
 
PDF
Beating the Spread: Time-Optimal Point Meshing
byDon Sheehy
 
PDF
Geometry, Topology, and all of Your Wildest Dreams Will Come True
byDon Sheehy
 
PDF
Minimax Rates for Homology Inference
byDon Sheehy
 
PDF
SOCG: Linear-Size Approximations to the Vietoris-Rips Filtration
byDon Sheehy
 
PDF
Topological Inference via Meshing
byDon Sheehy
 
PDF
Centerpoints Theory Lunch Talk
byDon Sheehy
 
PDF
Planar Graphis in 2.5 Dimensions
byDon Sheehy
 
On Nets and Meshes
byDon Sheehy
 
Linear Size Meshes
byDon Sheehy
 
Mesh Generation and Topological Data Analysis
byDon Sheehy
 
Linear-Size Approximations to the Vietoris-Rips Filtration - Presented at Uni...
byDon Sheehy
 
Characterizing the Distortion of Some Simple Euclidean Embeddings
byDon Sheehy
 
ATMCS: Linear-Size Approximations to the Vietoris-Rips Filtration
byDon Sheehy
 
Output-Sensitive Voronoi Diagrams and Delaunay Triangulations
byDon Sheehy
 
Ball Packings and Fat Voronoi Diagrams
byDon Sheehy
 
Overlay Stitch Meshing
byDon Sheehy
 
Beating the Spread: Time-Optimal Point Meshing
byDon Sheehy
 
Geometry, Topology, and all of Your Wildest Dreams Will Come True
byDon Sheehy
 
Minimax Rates for Homology Inference
byDon Sheehy
 
SOCG: Linear-Size Approximations to the Vietoris-Rips Filtration
byDon Sheehy
 
Topological Inference via Meshing
byDon Sheehy
 
Centerpoints Theory Lunch Talk
byDon Sheehy
 
Planar Graphis in 2.5 Dimensions
byDon Sheehy
 

Similar to New Bounds on the Size of Optimal Meshes

PPTX
Pattern classification
byGarisha Chowdhary
 
PDF
Problem Solving by Computer Finite Element Method
byPeter Herbert
 
PDF
A New Approach to Output-Sensitive Voronoi Diagrams and Delaunay Triangulations
byDon Sheehy
 
PPTX
Image Representation & Descriptors
byPundrikPatel
 
PDF
"Mesh of Periodic Minimal Surfaces in CGAL."
byVissarion Fisikopoulos
 
PPT
DIP_14_54_boundary extraction in dip .ppt
byitzkingpuneet
 
PDF
Two Dimensional Shape and Texture Quantification - Medical Image Processing
byChamod Mune
 
PDF
Lec09 hough
byBaliThorat1
 
PDF
Mesh Quality
byjulien_dompierre
 
PPTX
Image representation
byRahul Dadwal
 
PPTX
Computer graphics
byNanhen Verma
 
PPTX
Features image processing and Extaction
byAli A Jalil
 
PDF
Topological Inference via Meshing
byDon Sheehy
 
PDF
Hoip10 articulo surface reconstruction_upc
byTECNALIA Research & Innovation
 
PPTX
representation.pptx
byvijayalakshmi257551
 
PDF
Ijetcas14 567
byIasir Journals
 
PPT
Shape drawing algs
byMusawarNice
 
PPT
Fingerprint High Level Classification
byReza Rahimi
 
PDF
Loop snakesiv05
bysaulloribeiro
 
PDF
Four Side Distance: A New Fourier Shape Signature
byIJASCSE
 
Pattern classification
byGarisha Chowdhary
 
Problem Solving by Computer Finite Element Method
byPeter Herbert
 
A New Approach to Output-Sensitive Voronoi Diagrams and Delaunay Triangulations
byDon Sheehy
 
Image Representation & Descriptors
byPundrikPatel
 
"Mesh of Periodic Minimal Surfaces in CGAL."
byVissarion Fisikopoulos
 
DIP_14_54_boundary extraction in dip .ppt
byitzkingpuneet
 
Two Dimensional Shape and Texture Quantification - Medical Image Processing
byChamod Mune
 
Lec09 hough
byBaliThorat1
 
Mesh Quality
byjulien_dompierre
 
Image representation
byRahul Dadwal
 
Computer graphics
byNanhen Verma
 
Features image processing and Extaction
byAli A Jalil
 
Topological Inference via Meshing
byDon Sheehy
 
Hoip10 articulo surface reconstruction_upc
byTECNALIA Research & Innovation
 
representation.pptx
byvijayalakshmi257551
 
Ijetcas14 567
byIasir Journals
 
Shape drawing algs
byMusawarNice
 
Fingerprint High Level Classification
byReza Rahimi
 
Loop snakesiv05
bysaulloribeiro
 
Four Side Distance: A New Fourier Shape Signature
byIJASCSE
 

More from Don Sheehy

PDF
The Persistent Homology of Distance Functions under Random Projection
byDon Sheehy
 
PDF
Persistent Homology and Nested Dissection
byDon Sheehy
 
PDF
Geometric Separators and the Parabolic Lift
byDon Sheehy
 
PDF
Geometric and Topological Data Analysis
byDon Sheehy
 
PDF
Some Thoughts on Sampling
byDon Sheehy
 
PDF
Achieving Spatial Adaptivity while Searching for Approximate Nearest Neighbors
byDon Sheehy
 
PDF
Sensors and Samples: A Homological Approach
byDon Sheehy
 
PDF
The Centervertex Theorem (FWCG)
byDon Sheehy
 
PDF
Learning with Nets and Meshes
byDon Sheehy
 
PDF
A Multicover Nerve for Geometric Inference
byDon Sheehy
 
PDF
The Centervertex Theorem (CCCG)
byDon Sheehy
 
PPT
Flips in Computational Geometry
byDon Sheehy
 
The Persistent Homology of Distance Functions under Random Projection
byDon Sheehy
 
Persistent Homology and Nested Dissection
byDon Sheehy
 
Geometric Separators and the Parabolic Lift
byDon Sheehy
 
Geometric and Topological Data Analysis
byDon Sheehy
 
Some Thoughts on Sampling
byDon Sheehy
 
Achieving Spatial Adaptivity while Searching for Approximate Nearest Neighbors
byDon Sheehy
 
Sensors and Samples: A Homological Approach
byDon Sheehy
 
The Centervertex Theorem (FWCG)
byDon Sheehy
 
Learning with Nets and Meshes
byDon Sheehy
 
A Multicover Nerve for Geometric Inference
byDon Sheehy
 
The Centervertex Theorem (CCCG)
byDon Sheehy
 
Flips in Computational Geometry
byDon Sheehy
 

New Bounds on the Size of Optimal Meshes

  • 1.
    New Bounds on the Size of Optimal Meshes Don Sheehy Geometrica INRIA
  • 2.
  • 3.
    Mesh Generation 1 Decompose a volume into simplices.
  • 4.
    Mesh Generation 1 Decompose a volume into simplices. 2 Simplices should be quality.
  • 5.
    Mesh Generation 1 Decompose a volume into simplices. 2 Simplices should be quality.
  • 6.
    Mesh Generation 1 Decompose a volume into simplices. 2 Simplices should be quality. 3 Output should conform to input.
  • 7.
    Mesh Generation 1 Decompose a volume into simplices. 2 Simplices should be quality. 3 Output should conform to input.
  • 8.
  • 9.
  • 10.
  • 11.
    Mesh Generation Uses: PDEs via FEM Data Analysis
  • 12.
    Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes:
  • 13.
    Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle
  • 14.
    Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL
  • 15.
    Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL TetGen
  • 16.
    Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL TetGen Theoretical Guarantees:
  • 17.
    Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL TetGen Theoretical Guarantees: Sliver Removal
  • 18.
    Mesh Generation Uses: PDEs via FEM Data Analysis Good Codes: Triangle CGAL TetGen Theoretical Guarantees: Sliver Removal Surface Reconstruction
  • 19.
  • 20.
  • 21.
  • 22.
  • 23.
  • 24.
  • 25.
  • 26.
  • 27.
  • 28.
  • 29.
  • 30.
  • 31.
  • 32.
  • 33.
  • 34.
  • 35.
  • 36.
  • 37.
  • 38.
  • 39.
  • 40.
  • 41.
  • 42.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel
  • 43.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons:
  • 44.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination?
  • 45.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations?
  • 46.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations?
  • 47.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations?
  • 48.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations? How many points?
  • 49.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Accumulations? How many points?
  • 50.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Yes. Accumulations? How many points?
  • 51.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Yes. Accumulations? No. How many points?
  • 52.
    Local Refinement Algorithms Pros: Easy to implement Often Parallel Cons: Termination? Yes. Accumulations? No. How many points? This is what we’ll answer.
  • 53.
    The size ofan optimal mesh is given by the feature size measure.
  • 54.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P .
  • 55.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P .
  • 56.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P .
  • 57.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . x
  • 58.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . s( x) x lf
  • 59.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . x
  • 60.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . x lfs( x)
  • 61.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . dx Optimal Mesh Size = Θ Ω lfs(x)d x lfs( x)
  • 62.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . number of vertices dx Optimal Mesh Size = Θ Ω lfs(x)d x lfs( x)
  • 63.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . number of vertices dx Optimal Mesh Size = Θ Ω lfs(x)d hides simple exponential in d x lfs( x)
  • 64.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . number of vertices dx Optimal Mesh Size = Θ Ω lfs(x)d hides simple exponential in d dx The Feature Size Measure: µP (Ω) = lfsP (x)d Ω x lfs( x)
  • 65.
    The size ofan optimal mesh is given by the feature size measure. lfsP (x) := Distance to second nearest neighbor in P . number of vertices dx Optimal Mesh Size = Θ Ω lfs(x)d hides simple exponential in d dx The Feature Size Measure: µP (Ω) = lfsP (x)d Ω When is µP (Ω) = O(n)?
  • 66.
    A canonical badcase for meshing is two points in a big empty space.
  • 67.
    A canonical badcase for meshing is two points in a big empty space.
  • 68.
    A canonical badcase for meshing is two points in a big empty space.
  • 69.
    A canonical badcase for meshing is two points in a big empty space.
  • 70.
    A canonical badcase for meshing is two points in a big empty space.
  • 71.
    A canonical badcase for meshing is two points in a big empty space.
  • 72.
    A canonical badcase for meshing is two points in a big empty space.
  • 73.
    A canonical badcase for meshing is two points in a big empty space.
  • 74.
    A canonical badcase for meshing is two points in a big empty space.
  • 75.
    A canonical badcase for meshing is two points in a big empty space.
  • 76.
    The feature sizemeasure can be bounded in terms of the pacing.
  • 77.
    The feature sizemeasure can be bounded in terms of the pacing. Order the points.
  • 78.
    The feature sizemeasure can be bounded in terms of the pacing. Order the points.
  • 79.
    The feature sizemeasure can be bounded in terms of the pacing. Order the points.
  • 80.
    The feature sizemeasure can be bounded in terms of the pacing. Order the points.
  • 81.
    The feature sizemeasure can be bounded in terms of the pacing. Order the points.
  • 82.
    The feature sizemeasure can be bounded in terms of the pacing. Order the points.
  • 83.
    The feature sizemeasure can be bounded in terms of the pacing. pi Order the points.
  • 84.
    The feature sizemeasure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi )
  • 85.
    The feature sizemeasure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi ) b = pi − 2NN(pi )
  • 86.
    The feature sizemeasure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi ) b = pi − 2NN(pi ) b The pacing of the ith point is φi = a .
  • 87.
    The feature sizemeasure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi ) b = pi − 2NN(pi ) b The pacing of the ith point is φi = a . Let φ be the geometric mean, so log φi = n log φ.
  • 88.
    The feature sizemeasure can be bounded in terms of the pacing. pi Order the points. a = pi − NN(pi ) b = pi − 2NN(pi ) b The pacing of the ith point is φi = a . Let φ be the geometric mean, so log φi = n log φ. φ is the pacing of the ordering.
  • 89.
    The trick isto write the feature size measure as a telescoping sum.
  • 90.
    The trick isto write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi }
  • 91.
    The trick isto write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3
  • 92.
    The trick isto write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point.
  • 93.
    The trick isto write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point. µPi (Ω) − µPi−1 (Ω) = Θ(1 + log φi )
  • 94.
    The trick isto write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point. µPi (Ω) − µPi−1 (Ω) = Θ(1 + log φi ) n log φi = n log φ i=3
  • 95.
    The trick isto write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point. µPi (Ω) − µPi−1 (Ω) = Θ(1 + log φi ) n log φi = n log φ Θ(n + n log φ) i=3
  • 96.
    The trick isto write the feature size measure as a telescoping sum. Pi = {p1 , . . . , pi } n µ P = µ P2 + µPi − µPi−1 i=3 effect of adding the ith point. µPi (Ω) − µPi−1 (Ω) = Θ(1 + log φi ) n log φi = n log φ Θ(n + n log φ) i=3 d Previous bound: O(n + φ n).
  • 97.
    Pacing analysis hasalready led to new results.
  • 98.
    Pacing analysis hasalready led to new results. The Scaffold Theorem (SODA 2009) Given n points well-spaced on a surface, the volume mesh has size O(n).
  • 99.
    Pacing analysis hasalready led to new results. The Scaffold Theorem (SODA 2009) Given n points well-spaced on a surface, the volume mesh has size O(n). Time-Optimal Point Meshing (SoCG 2011) Build a mesh in O(n log n + m) time. Algorithm explicitly computes the pacing for each insertion.
  • 100.
  • 101.
    Some takeaway messages: 1 The amortized change in the number of vertices in a mesh as a result of adding one new point is determined by the pacing of that point.
  • 102.
    Some takeaway messages: 1 The amortized change in the number of vertices in a mesh as a result of adding one new point is determined by the pacing of that point. 2 Point sets that admit linear size meshes are exactly those with constant pacing.
  • 103.
    Some takeaway messages: 1 The amortized change in the number of vertices in a mesh as a result of adding one new point is determined by the pacing of that point. 2 Point sets that admit linear size meshes are exactly those with constant pacing. Thank you.
  • 106.
  • 107.
    Mesh Generation 13 Decompose a domain into simple elements.
  • 108.
    Mesh Generation 13 Decompose a domain into simple elements.
  • 109.
    Mesh Generation 13 Decompose a domain Mesh Quality into simple elements. Radius/Edge < const
  • 110.
    Mesh Generation 13 Decompose a domain Mesh Quality into simple elements. X ✓ X Radius/Edge < const
  • 111.
    Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const
  • 112.
    Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const
  • 113.
    Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const
  • 114.
    Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const
  • 115.
    Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const Voronoi Diagram
  • 116.
    Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const Voronoi Diagram OutRadius/InRadius < const
  • 117.
    Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const X ✓ Voronoi Diagram OutRadius/InRadius < const
  • 118.
    Mesh Generation 13 Decompose a domain Mesh Quality Conforming to Input into simple elements. X ✓ X Radius/Edge < const X ✓ Voronoi Diagram OutRadius/InRadius < const
  • 119.
    Optimal meshing addsthe fewest points to make all Voronoi cells fat.* * Equivalent to radius-edge condition on Delaunay simplices.
  • 120.
    Optimal meshing addsthe fewest points to make all Voronoi cells fat.* * Equivalent to radius-edge condition on Delaunay simplices.
  • 121.
    Optimal meshing addsthe fewest points to make all Voronoi cells fat.* * Equivalent to radius-edge condition on Delaunay simplices.
  • 122.
    Optimal meshing addsthe fewest points to make all Voronoi cells fat.* * Equivalent to radius-edge condition on Delaunay simplices.
  • 123.
    Meshing Points 15 Input: P ⊂ Rd Output: M ⊃ P with a “nice” Voronoi diagram n = |P |, m = |M |
  • 124.
    Meshing Points 15 Input: P ⊂ Rd Output: M ⊃ P with a “nice” Voronoi diagram n = |P |, m = |M |
  • 125.
    Meshing Points 15 Input: P ⊂ Rd Output: M ⊃ P with a “nice” Voronoi diagram n = |P |, m = |M |
  • 126.
    Meshing Points 15 Input: P ⊂ Rd Output: M ⊃ P with a “nice” Voronoi diagram n = |P |, m = |M |
  • 127.
    How to provea meshing algorithm is optimal.16
  • 128.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P
  • 129.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P
  • 130.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P x
  • 131.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P x fP (x)
  • 132.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P x
  • 133.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P ( x) x fP
  • 134.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P
  • 135.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d
  • 136.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d “No 2 points too close together” “Optimal Size Output”
  • 137.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d “No 2 points too close together” “Optimal Size Output” v
  • 138.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d “No 2 points too close together” “Optimal Size Output” v fM (v)
  • 139.
    How to provea meshing algorithm is optimal.16 The Ruppert Feature Size: fP (x) := distance to 2nd NN of x in P dx For all v ∈ M, fM (v) ≥ KfP (v) m=Θ Ω fP (x)d “No 2 points too close together” “Optimal Size Output” v ( v) fM (v) fP