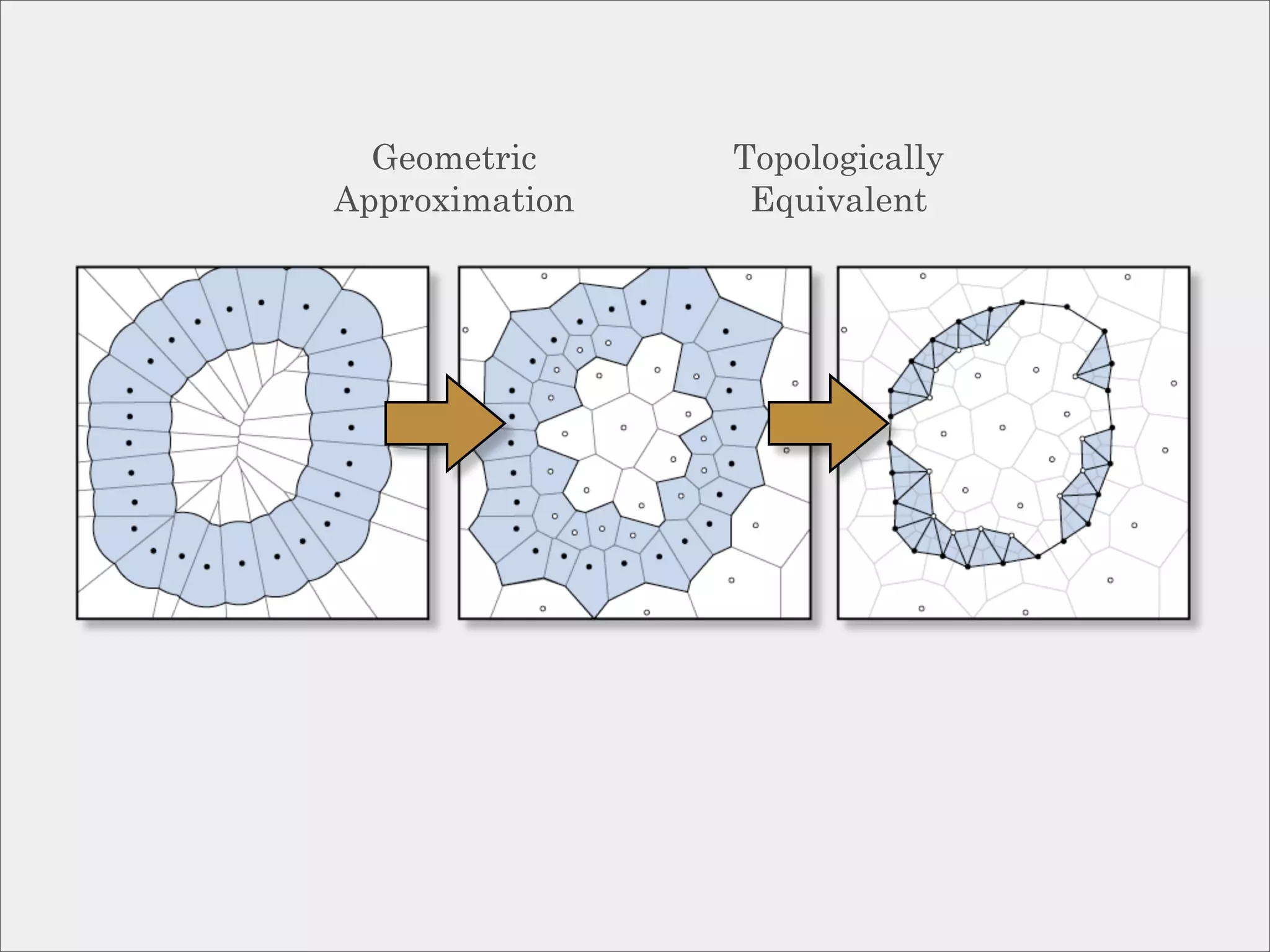
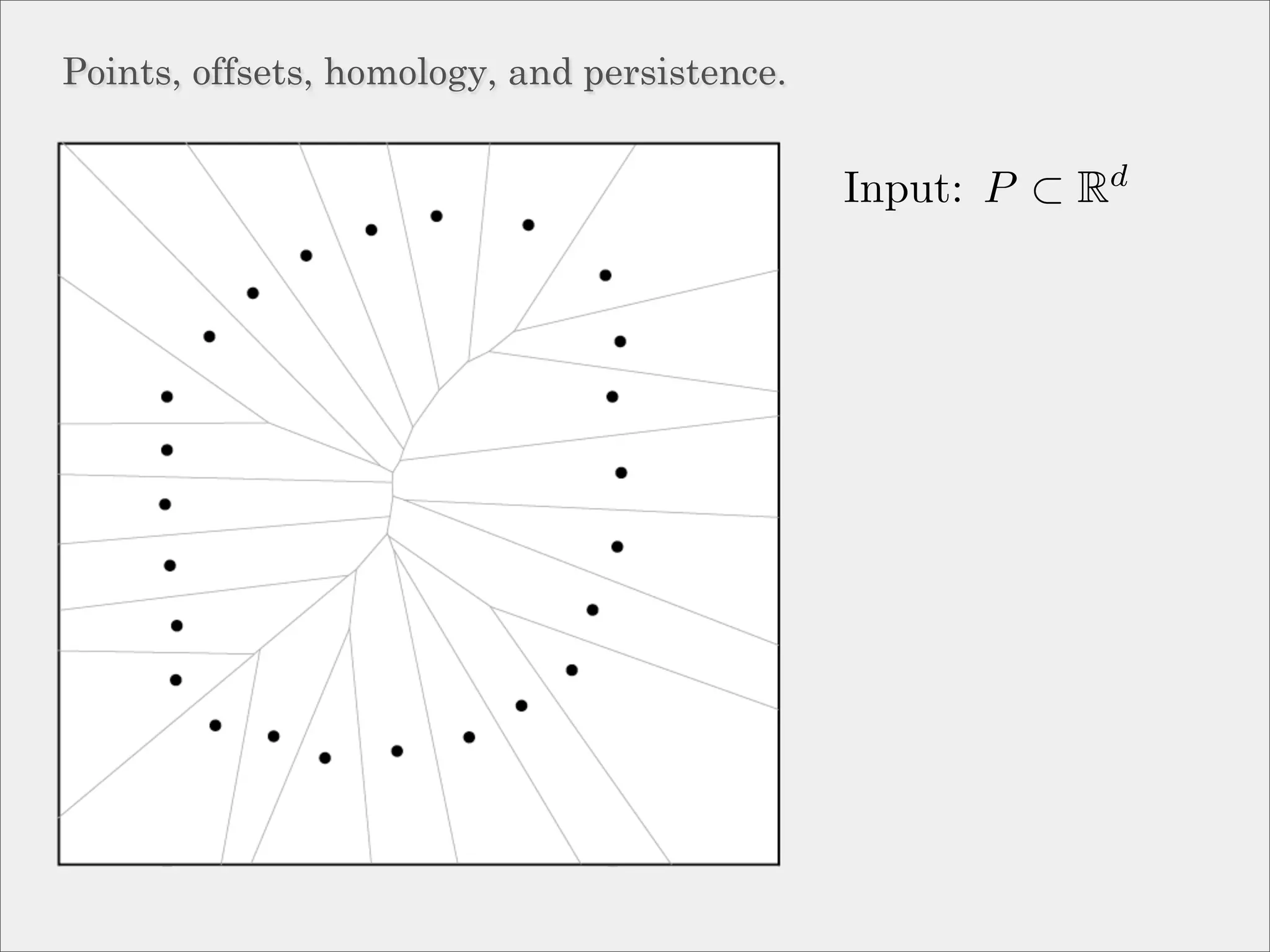
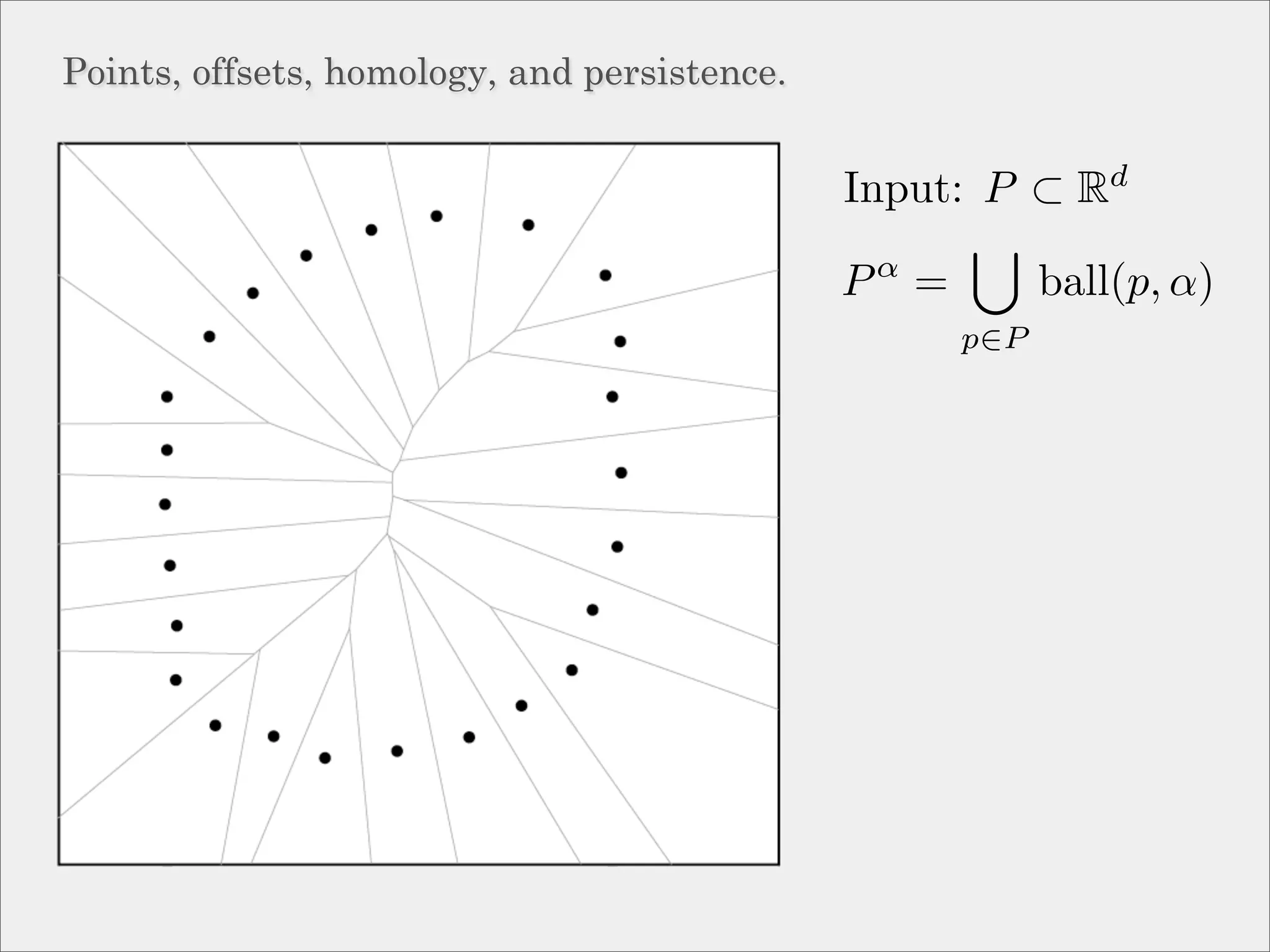
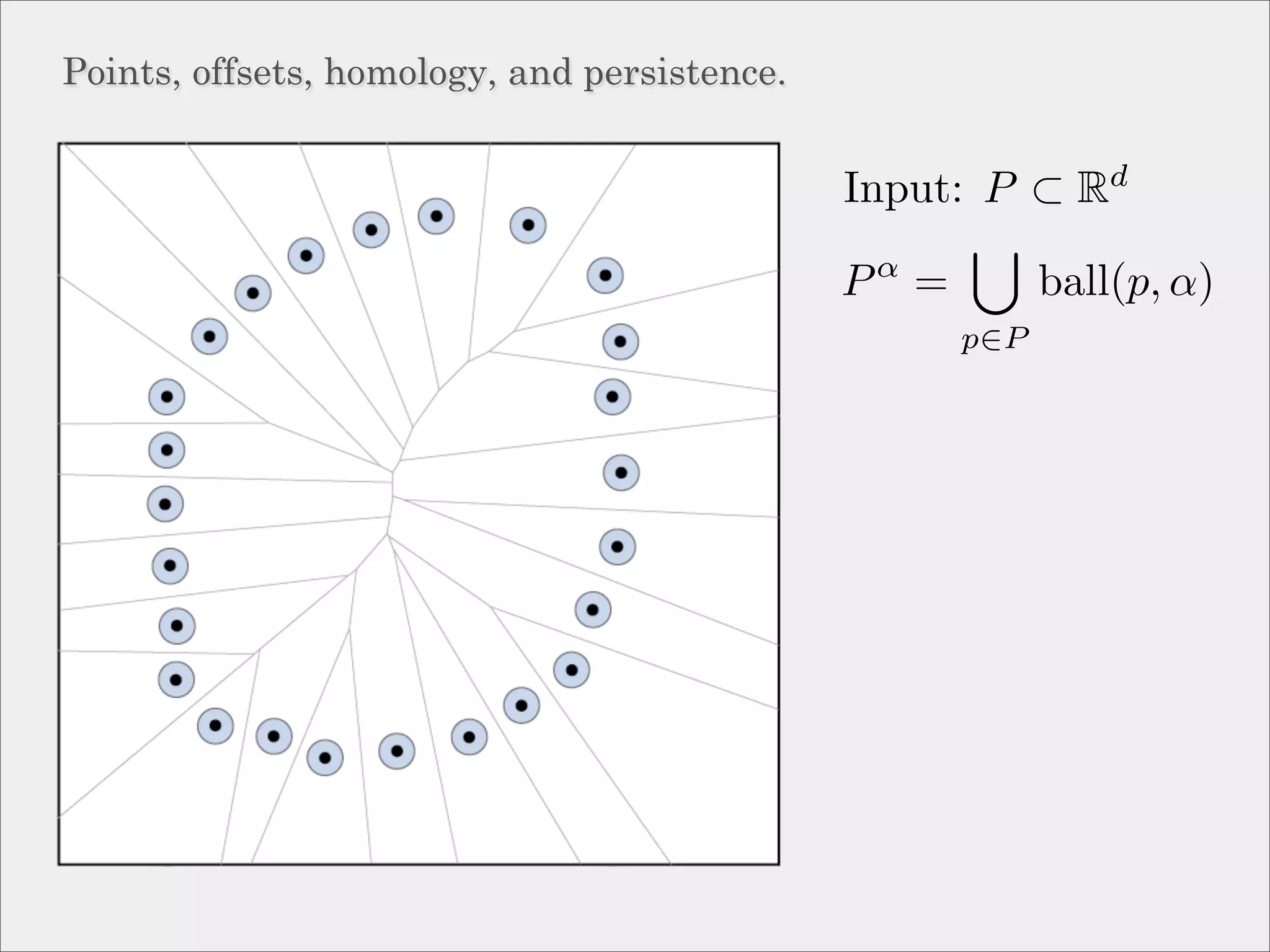
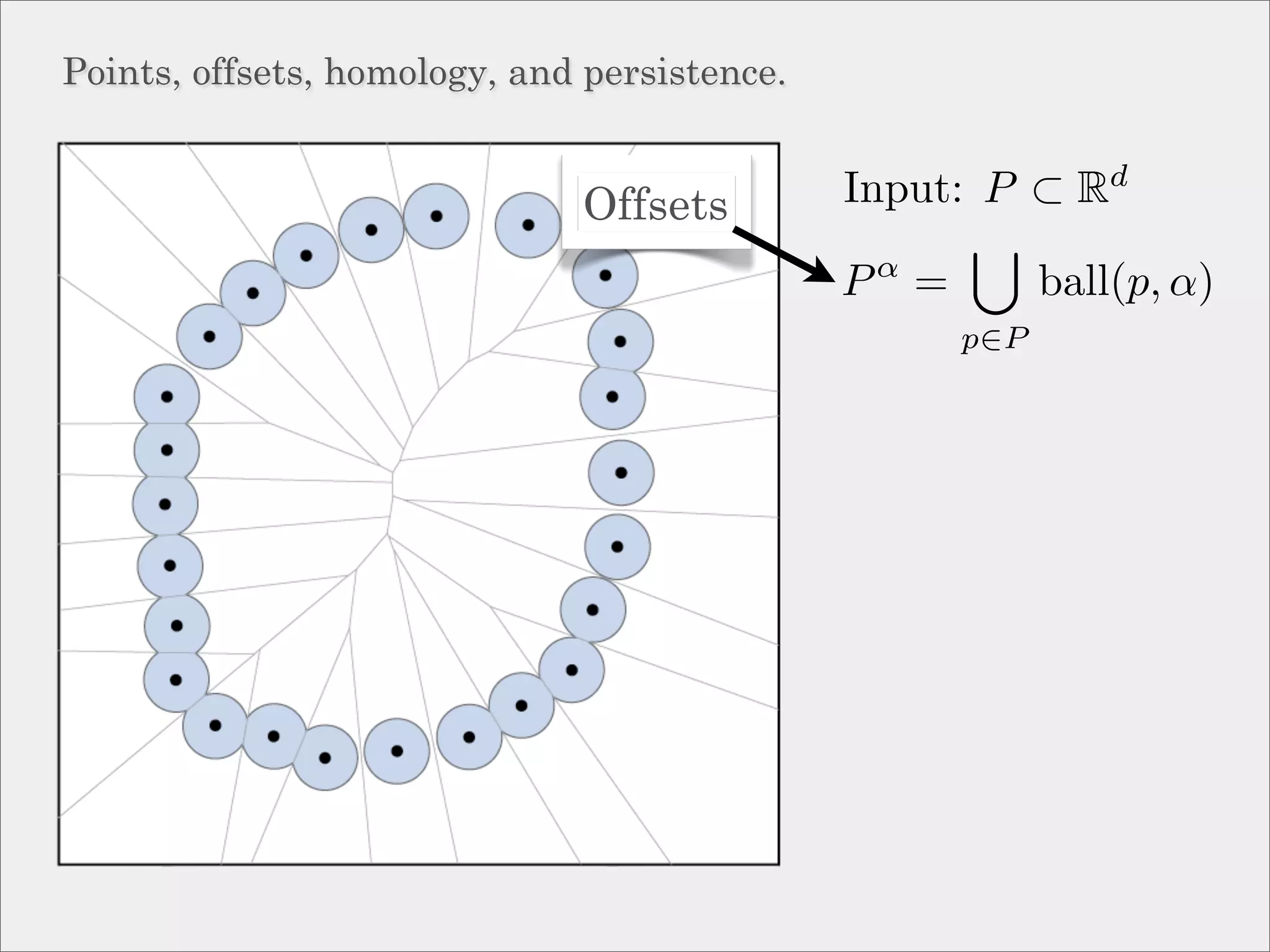
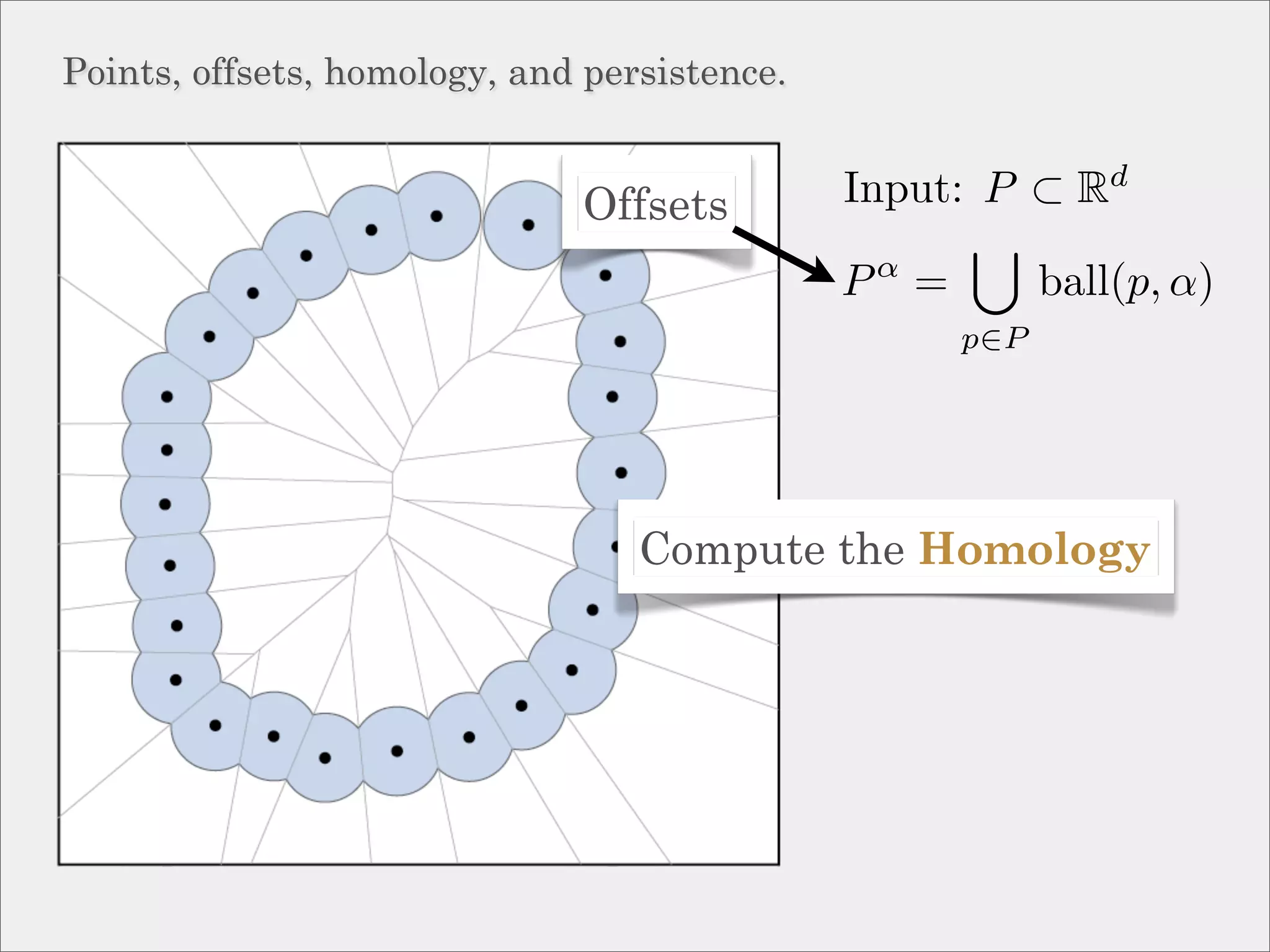
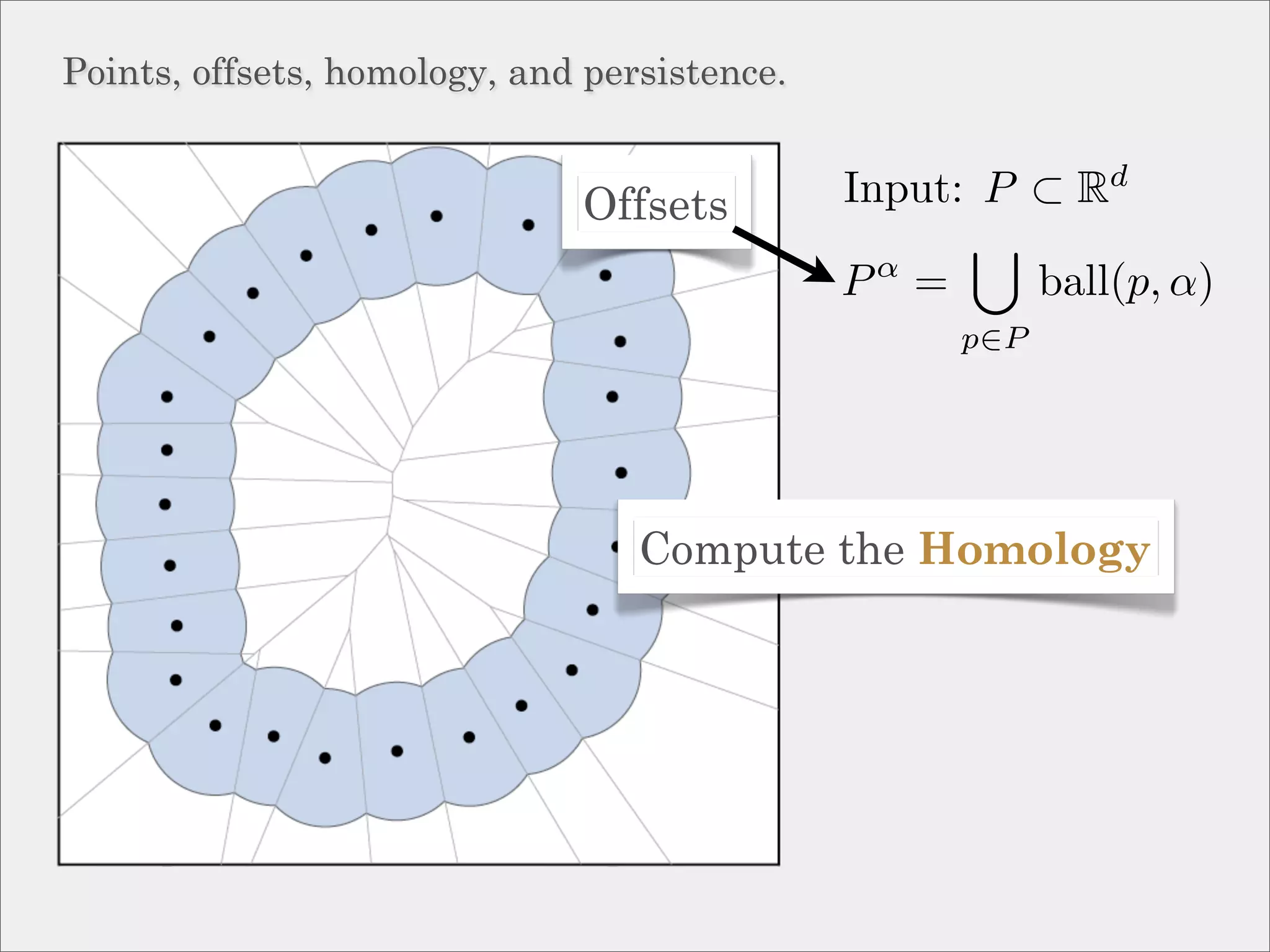
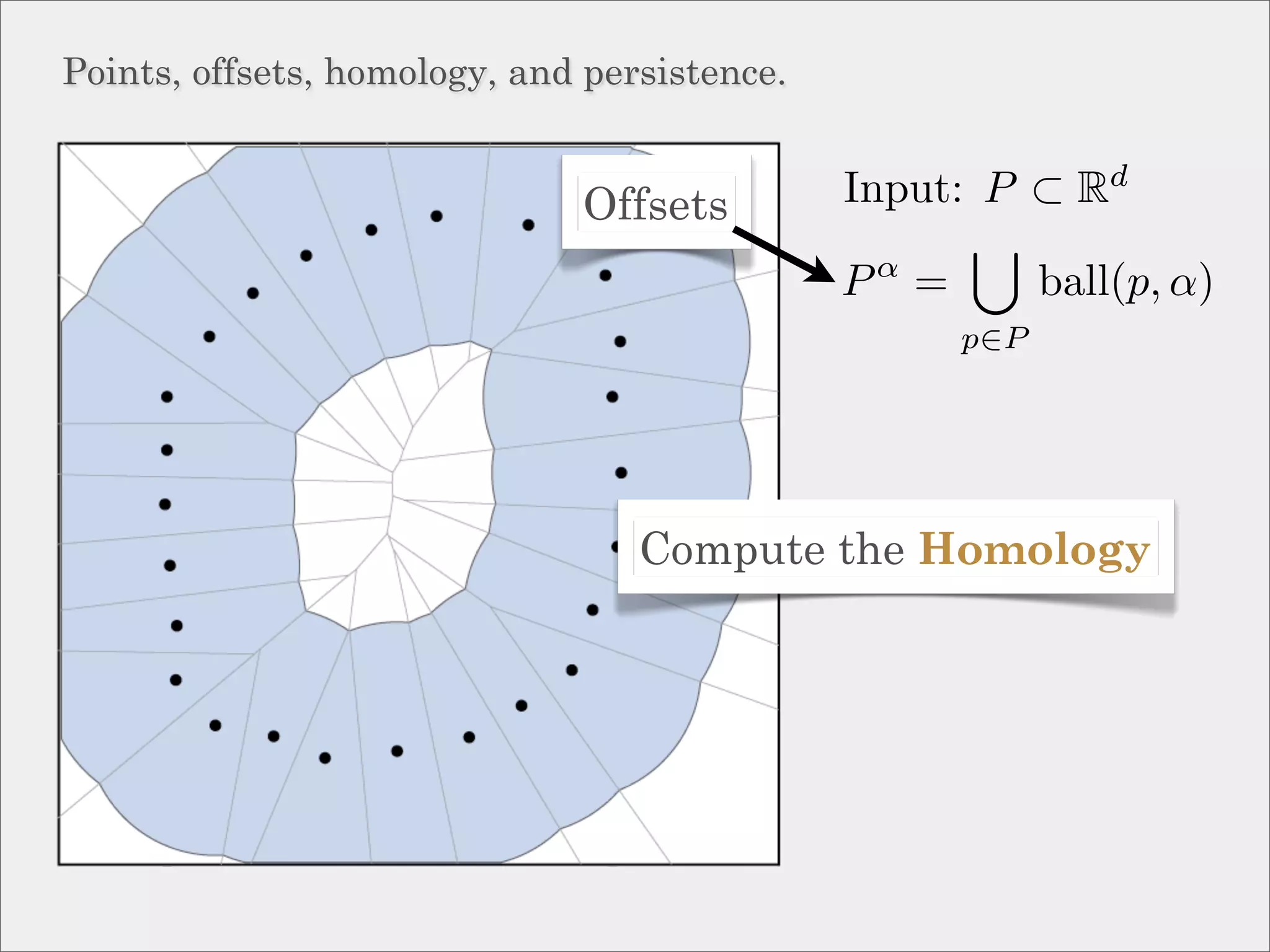
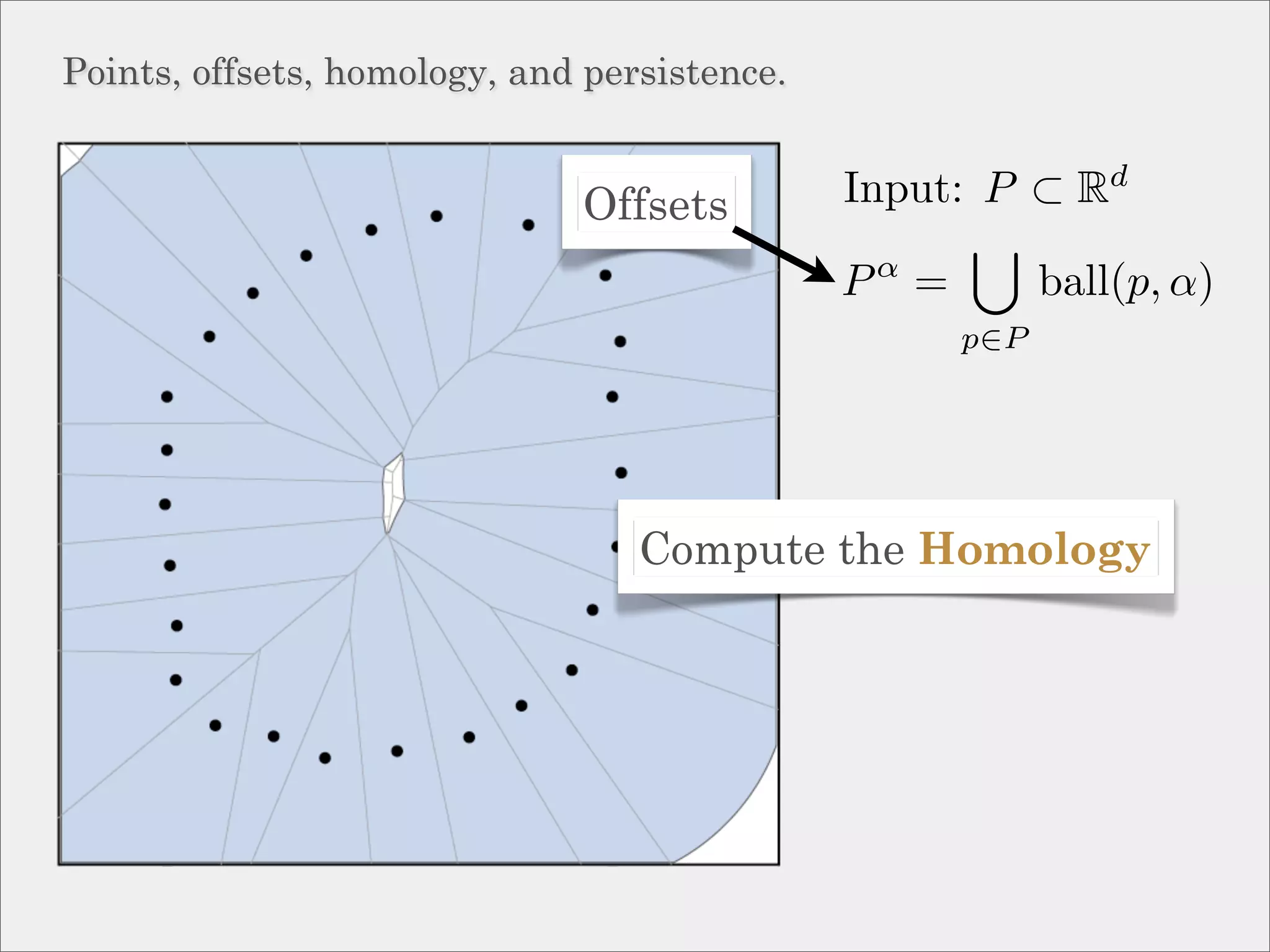
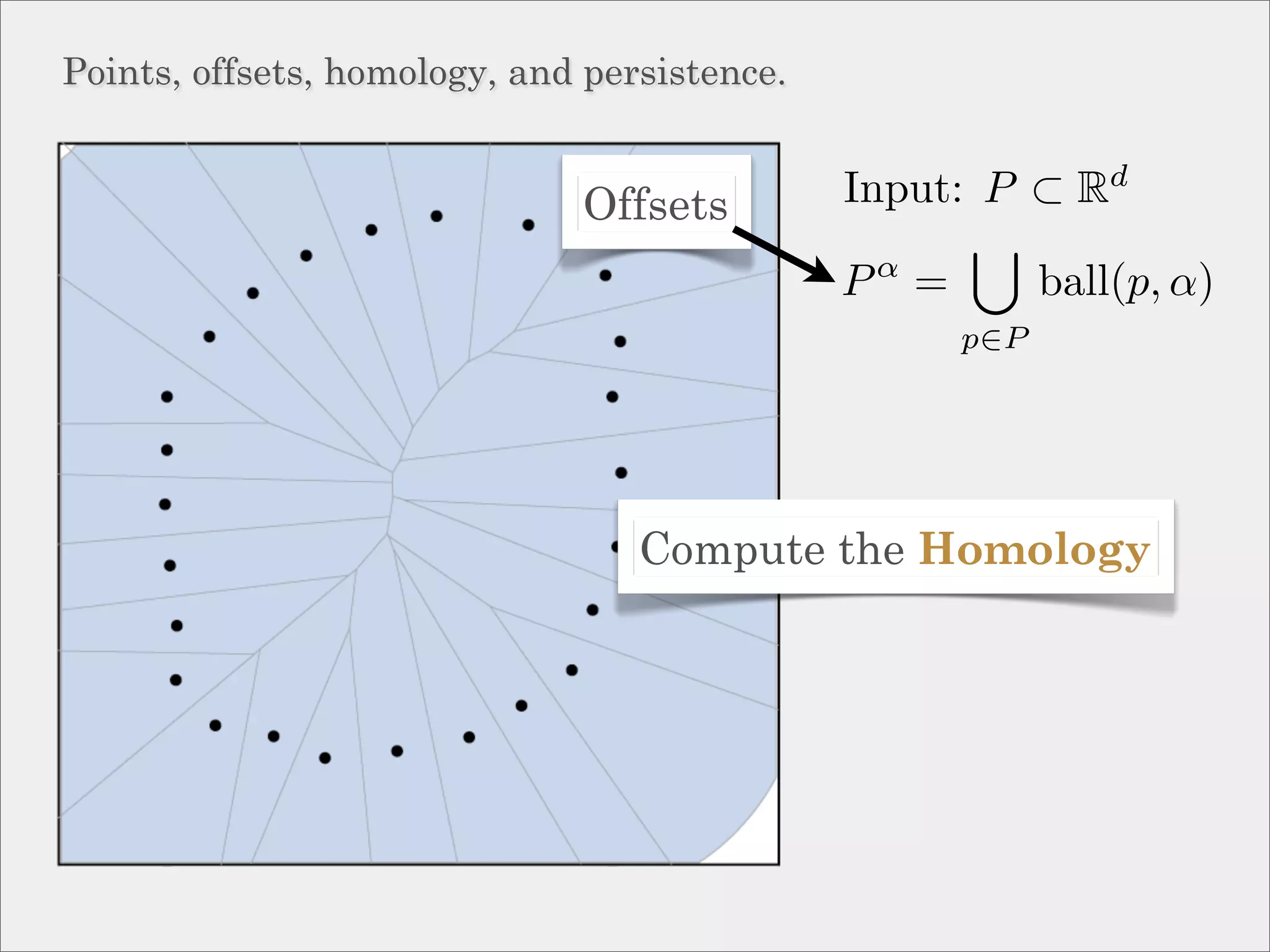
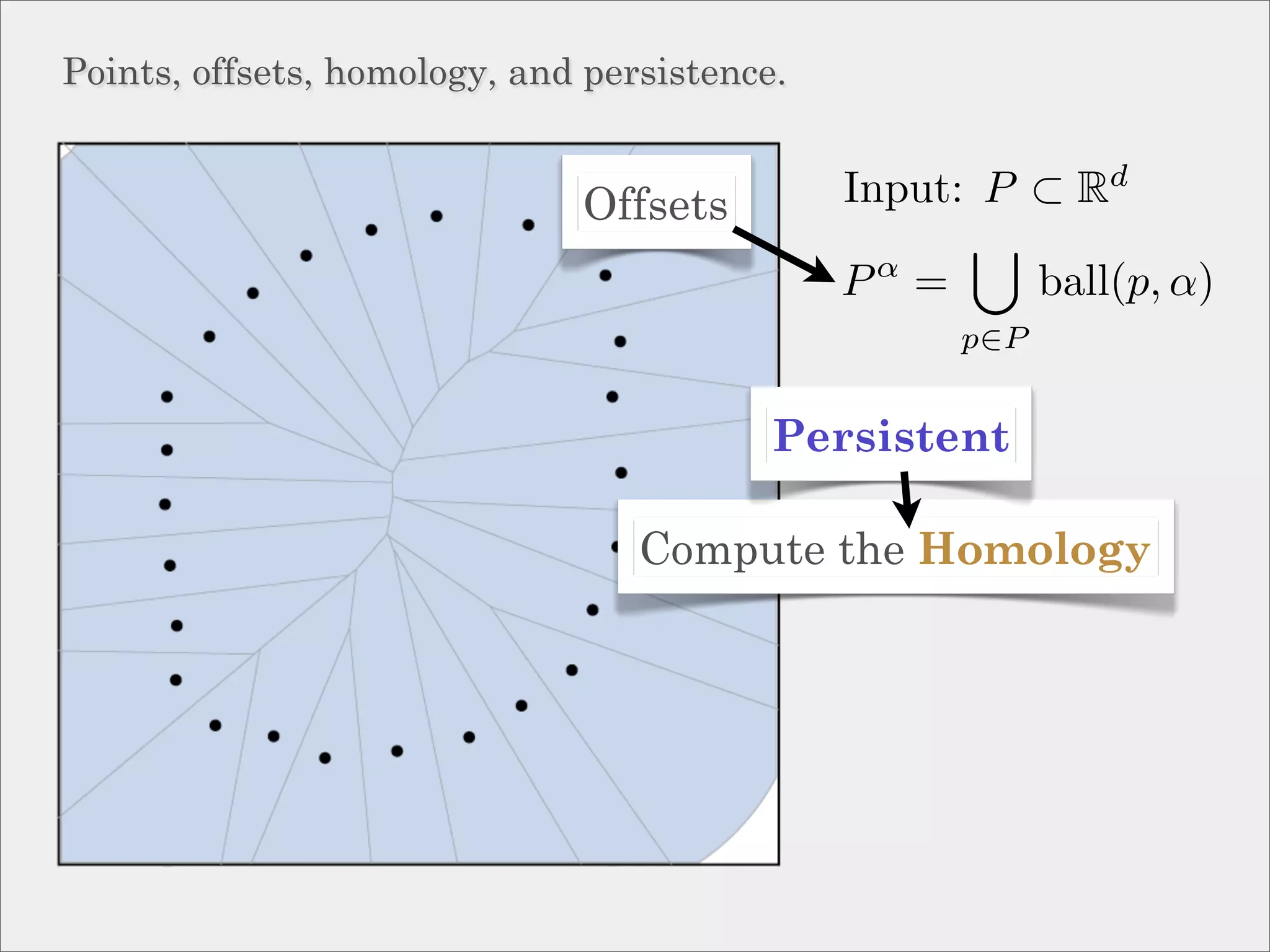
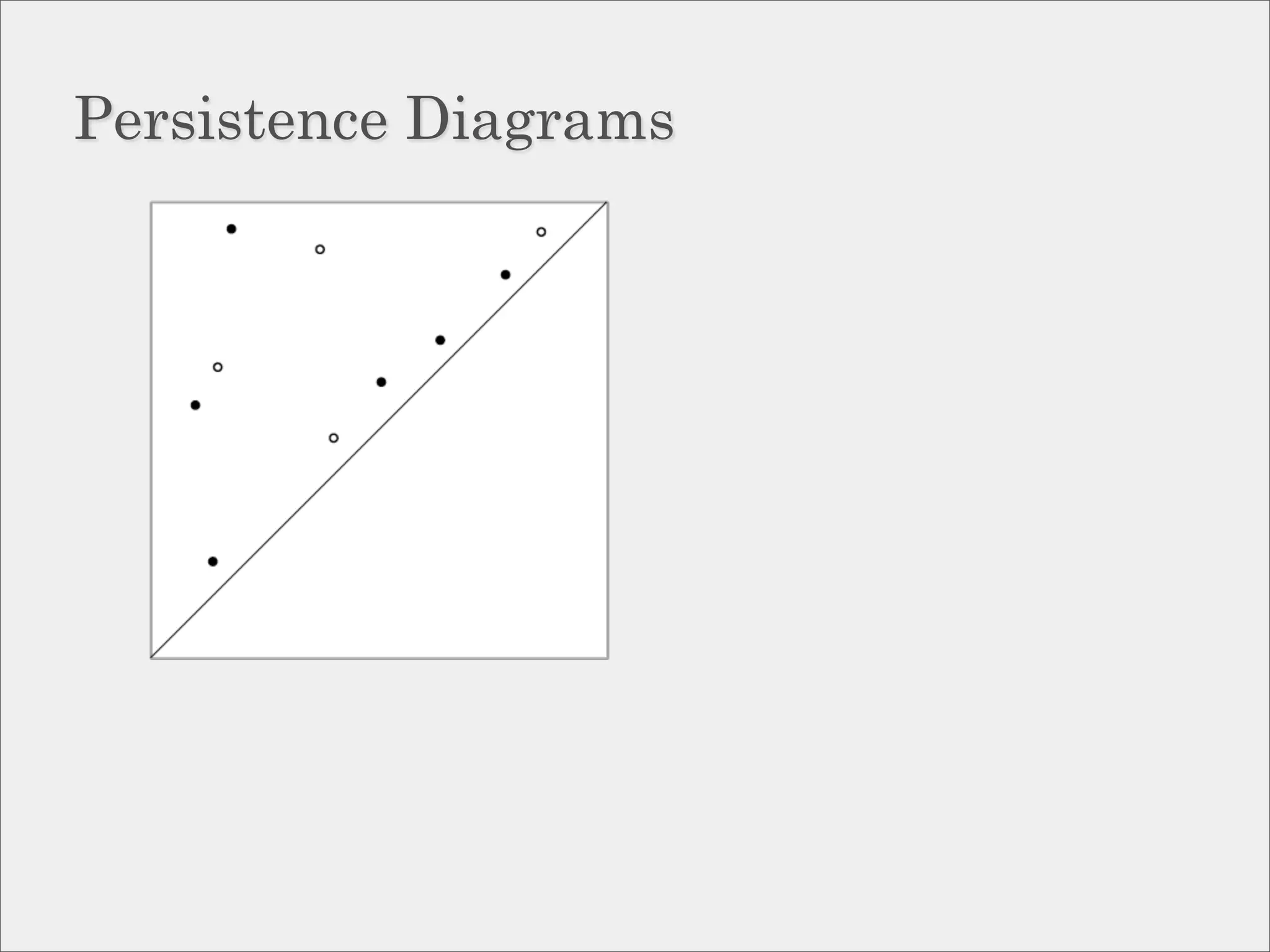
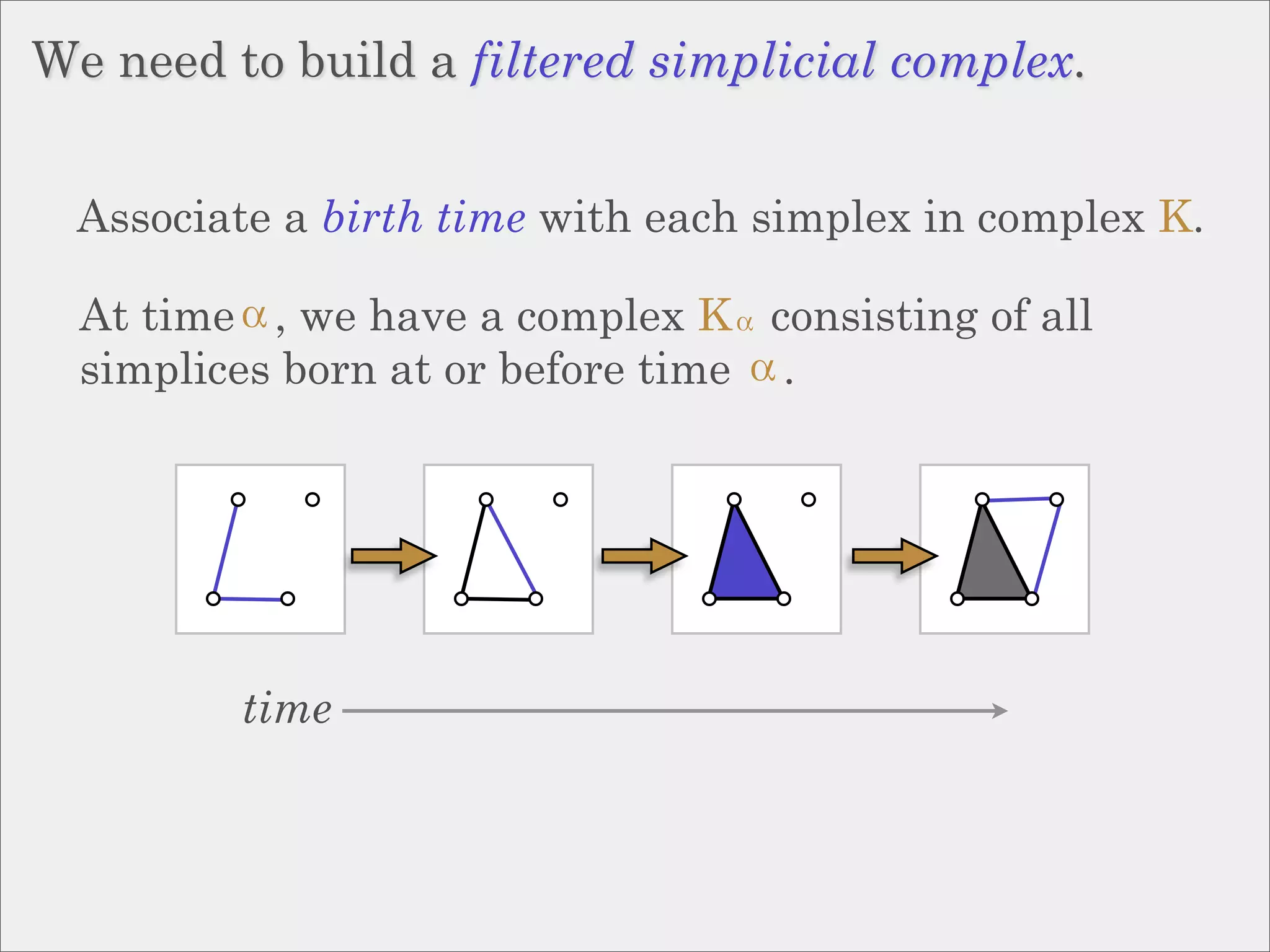
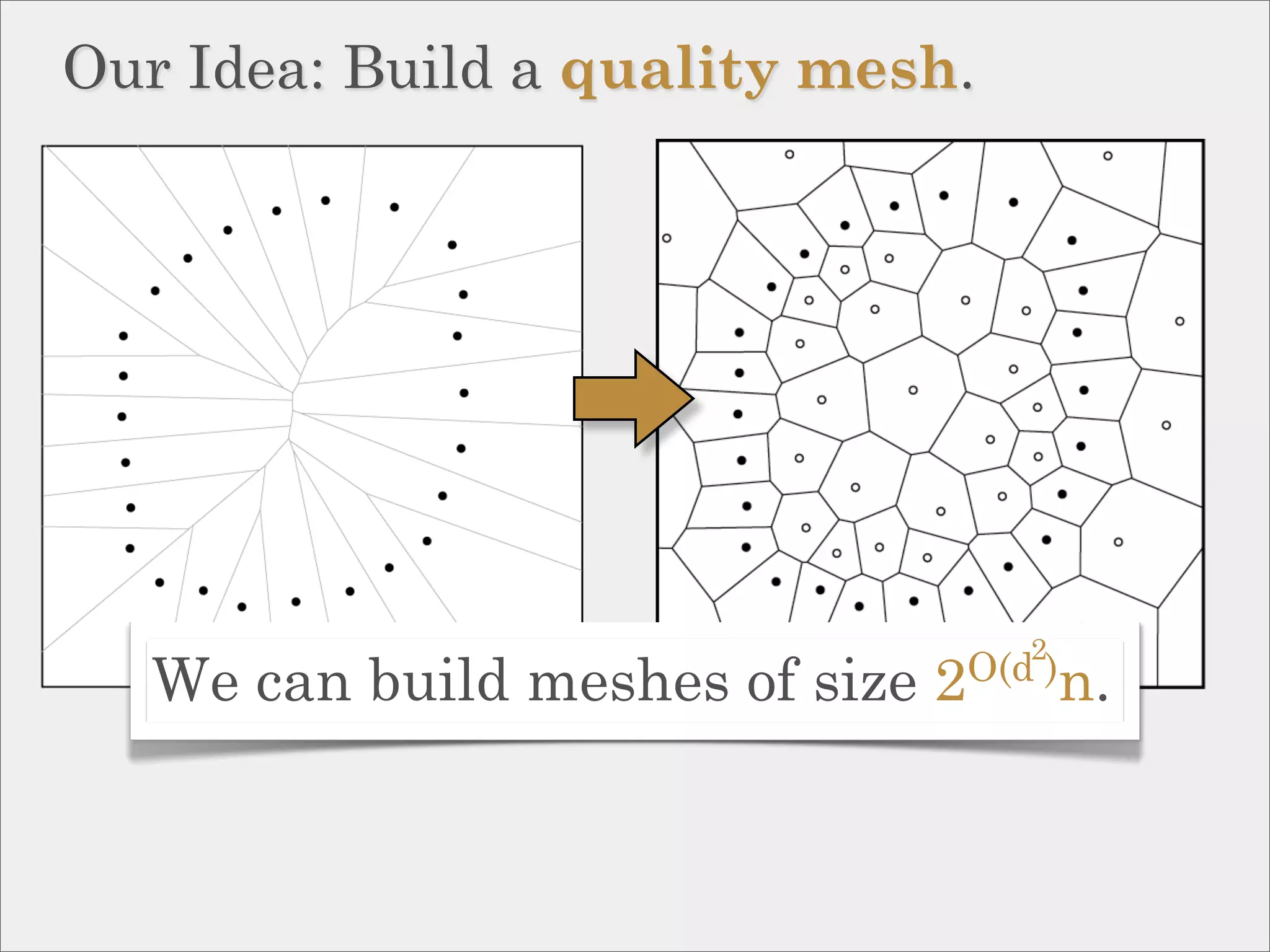
The document discusses topological inference through meshing, focusing on generating persistent homology from point data in Euclidean space. It reviews techniques for constructing meshes that can efficiently capture the object's topology, detailing geometric and topological phases, various filtration methods, and notable theorems regarding mesh quality and computational efficiency. Additionally, it addresses approximation strategies via interleaving to ensure close relationships between different filtrations.

1. Topological Inference via Meshing
Benoit Hudson, Gary Miller, Steve Oudot and Don Sheehy
SoCG 2010

2. Mesh Generation
and
Persistent Homology

3. The Problem
Input: Points in Euclidean space sampled from some
unknown object.
Output: Information about the topology of the
unknown object.

4. Points, offsets, homology, and persistence.

5. Points, offsets, homology, and persistence.
Input: P ⊂ Rd

6. Points, offsets, homology, and persistence.
Input: P ⊂ Rd
α
P = ball(p, α)
p∈P

7. Points, offsets, homology, and persistence.
Input: P ⊂ Rd
α
P = ball(p, α)
p∈P

8. Points, offsets, homology, and persistence.
Input: P ⊂ Rd
α
P = ball(p, α)
p∈P

9. Points, offsets, homology, and persistence.
Offsets Input: P ⊂ Rd
α
P = ball(p, α)
p∈P

10. Points, offsets, homology, and persistence.
Offsets Input: P ⊂ Rd
α
P = ball(p, α)
p∈P
Compute the Homology

11. Points, offsets, homology, and persistence.
Offsets Input: P ⊂ Rd
α
P = ball(p, α)
p∈P
Compute the Homology

12. Points, offsets, homology, and persistence.
Offsets Input: P ⊂ Rd
α
P = ball(p, α)
p∈P
Compute the Homology

13. Points, offsets, homology, and persistence.
Offsets Input: P ⊂ Rd
α
P = ball(p, α)
p∈P
Compute the Homology

14. Points, offsets, homology, and persistence.
Offsets Input: P ⊂ Rd
α
P = ball(p, α)
p∈P
Compute the Homology

15. Points, offsets, homology, and persistence.
Offsets Input: P ⊂ Rd
α
P = ball(p, α)
p∈P
Compute the Homology

16. Points, offsets, homology, and persistence.
Offsets Input: P ⊂ Rd
α
P = ball(p, α)
p∈P
Persistent
Compute the Homology

17. Persistence Diagrams

18. Persistence Diagrams

19. Persistence Diagrams
Bottleneck Distance
d∞ = max |pi − qi |∞
B
i

20. Approximate
Persistence Diagrams
Bottleneck Distance
d∞ = max |pi − qi |∞
B
i

21. Approximate Birth and Death times
Persistence Diagrams differ by a constant factor.
Bottleneck Distance
d∞ = max |pi − qi |∞
B
i

22. Approximate Birth and Death times
Persistence Diagrams differ by a constant factor.
Bottleneck Distance
d∞ = max |pi − qi |∞
B
i
This is just the bottleneck distance of the log-scale diagrams.

23. Approximate Birth and Death times
Persistence Diagrams differ by a constant factor.
Bottleneck Distance
d∞ = max |pi − qi |∞
B
i
This is just the bottleneck distance of the log-scale diagrams.
log a − log b < ε
a
log b < ε
a
b <1+ε

24. We need to build a filtered simplicial complex.
Associate a birth time with each simplex in complex K.
At time , we have a complex K consisting of all
simplices born at or before time .
time

25. There are two phases, one is geometric the
other is topological.
Geometry Topology
(linear algebra)
Build a filtration, i.e. Compute the
a filtered simplicial persistence diagram
complex. (Run the Persistence Algorithm).

26. There are two phases, one is geometric the
other is topological.
Geometry Topology
(linear algebra)
Build a filtration, i.e. Compute the
a filtered simplicial persistence diagram
complex. (Run the Persistence Algorithm).
We’ll focus on this side.

27. There are two phases, one is geometric the
other is topological.
Geometry Topology
(linear algebra)
Build a filtration, i.e. Compute the
a filtered simplicial persistence diagram
complex. (Run the Persistence Algorithm).
We’ll focus on this side. Running time: O(N3).
N is the size of the complex.

28. Idea 1: Use the Delaunay Triangulation

29. Idea 1: Use the Delaunay Triangulation
Good: It works, (alpha-complex filtration).

30. Idea 1: Use the Delaunay Triangulation
Good: It works, (alpha-complex filtration).
Bad: It can have size nO(d).

31. Idea 2: Connect up everything close.

32. Idea 2: Connect up everything close.
Čech Filtration: Add a k-simplex for every k+1
points that have a smallest enclosing ball of
radius at most .

33. Idea 2: Connect up everything close.
Čech Filtration: Add a k-simplex for every k+1
points that have a smallest enclosing ball of
radius at most .
Rips Filtration: Add a k-simplex for every k+1
points that have all pairwise distances at
most .

34. Idea 2: Connect up everything close.
Čech Filtration: Add a k-simplex for every k+1
points that have a smallest enclosing ball of
radius at most .
Rips Filtration: Add a k-simplex for every k+1
points that have all pairwise distances at
most .
Still nd, but we can quit early.

35. Our Idea: Build a quality mesh.

36. Our Idea: Build a quality mesh.

37. Our Idea: Build a quality mesh.
2
We can build meshes of size 2 O(d )n.

38. Meshing Counter-intuition
Delaunay Refinement
can take less time and space than
Delaunay Triangulation.

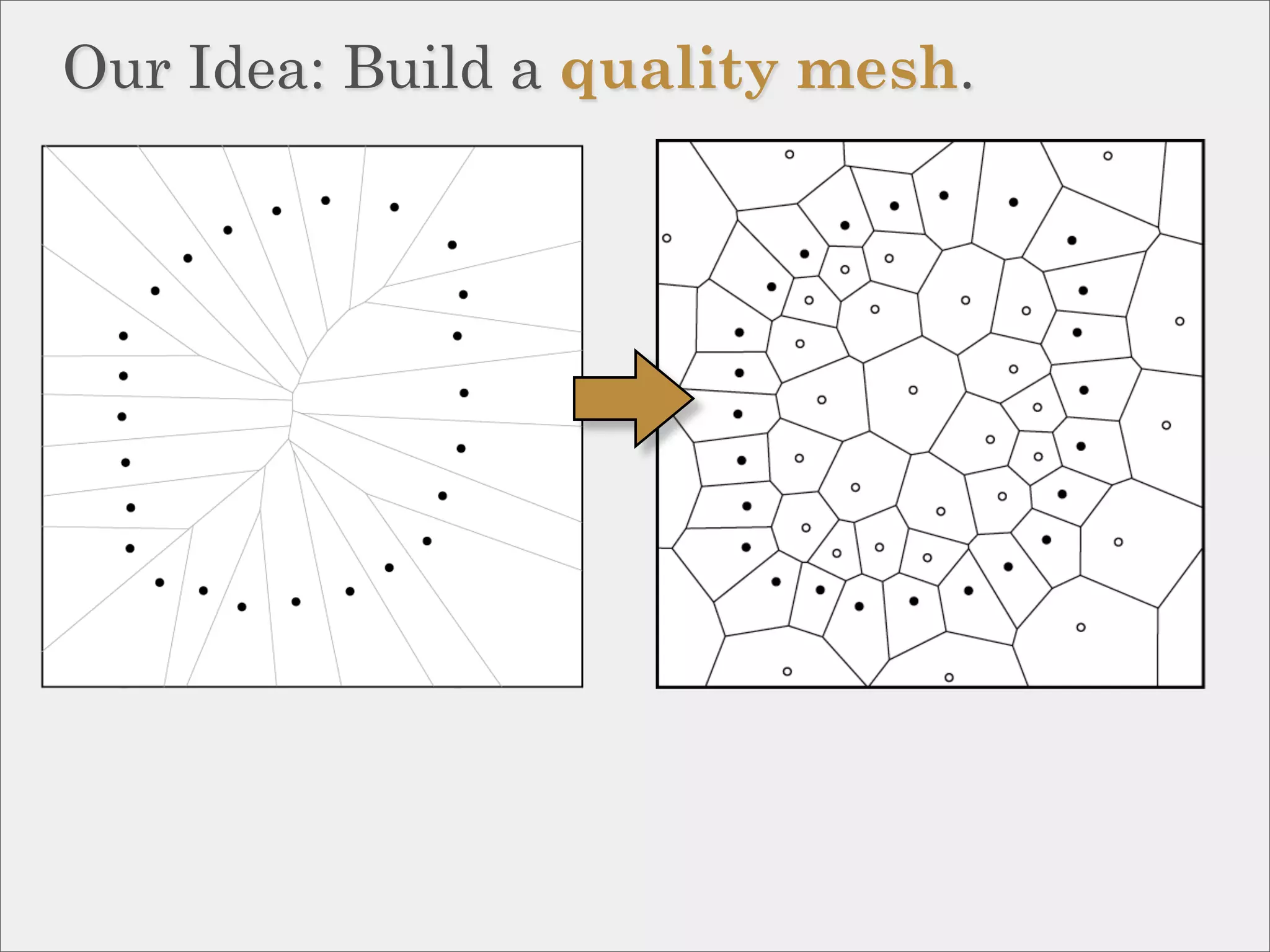
39. Meshing Counter-intuition
Delaunay Refinement
can take less time and space than
Delaunay Triangulation.
Theorem [Hudson, Miller, Phillips, ’06]:
A quality mesh of a point set can
be constructed in O(n log ∆) time,
where ∆ is the spread.

40. Meshing Counter-intuition
Delaunay Refinement
can take less time and space than
Delaunay Triangulation.
Theorem [Hudson, Miller, Phillips, ’06]:
A quality mesh of a point set can
be constructed in O(n log ∆) time,
where ∆ is the spread.
Theorem [Miller, Phillips, Sheehy, ’08]:
A quality mesh of a well-paced
point set has size O(n).

41. The α-mesh filtration
1. Build a mesh M.
2. Assign birth times to
vertices based on distance to P
(special case points very close to P).
3. For each simplex s of Del(M),
let birth(s) be the min birth
time of its vertices.
4. Feed this filtered complex to
the persistence algorithm.

42. The α-mesh filtration
1. Build a mesh M.
2. Assign birth times to
vertices based on distance to P
(special case points very close to P).
3. For each simplex s of Del(M),
let birth(s) be the min birth
time of its vertices.
4. Feed this filtered complex to
the persistence algorithm.

43. The α-mesh filtration
1. Build a mesh M.
2. Assign birth times to
vertices based on distance to P
(special case points very close to P).
3. For each simplex s of Del(M),
let birth(s) be the min birth
time of its vertices.
4. Feed this filtered complex to
the persistence algorithm.

44. The α-mesh filtration
1. Build a mesh M.
2. Assign birth times to
vertices based on distance to P
(special case points very close to P).
3. For each simplex s of Del(M),
let birth(s) be the min birth
time of its vertices.
4. Feed this filtered complex to
the persistence algorithm.

45. The α-mesh filtration
1. Build a mesh M.
2. Assign birth times to
vertices based on distance to P
(special case points very close to P).
3. For each simplex s of Del(M),
let birth(s) be the min birth
time of its vertices.
4. Feed this filtered complex to
the persistence algorithm.

46. The α-mesh filtration
1. Build a mesh M.
2. Assign birth times to
vertices based on distance to P
(special case points very close to P).
3. For each simplex s of Del(M),
let birth(s) be the min birth
time of its vertices.
4. Feed this filtered complex to
the persistence algorithm.

47. The α-mesh filtration
1. Build a mesh M.
2. Assign birth times to
vertices based on distance to P
(special case points very close to P).
3. For each simplex s of Del(M),
let birth(s) be the min birth
time of its vertices.
4. Feed this filtered complex to
the persistence algorithm.

48. Approximation via interleaving.

49. Approximation via interleaving.
Definition:
Two filtrations, {Pα } and {Qα } are
ε-interleaved if Pα−ε ⊆ Qα ⊆ Pα+ε
for all α.

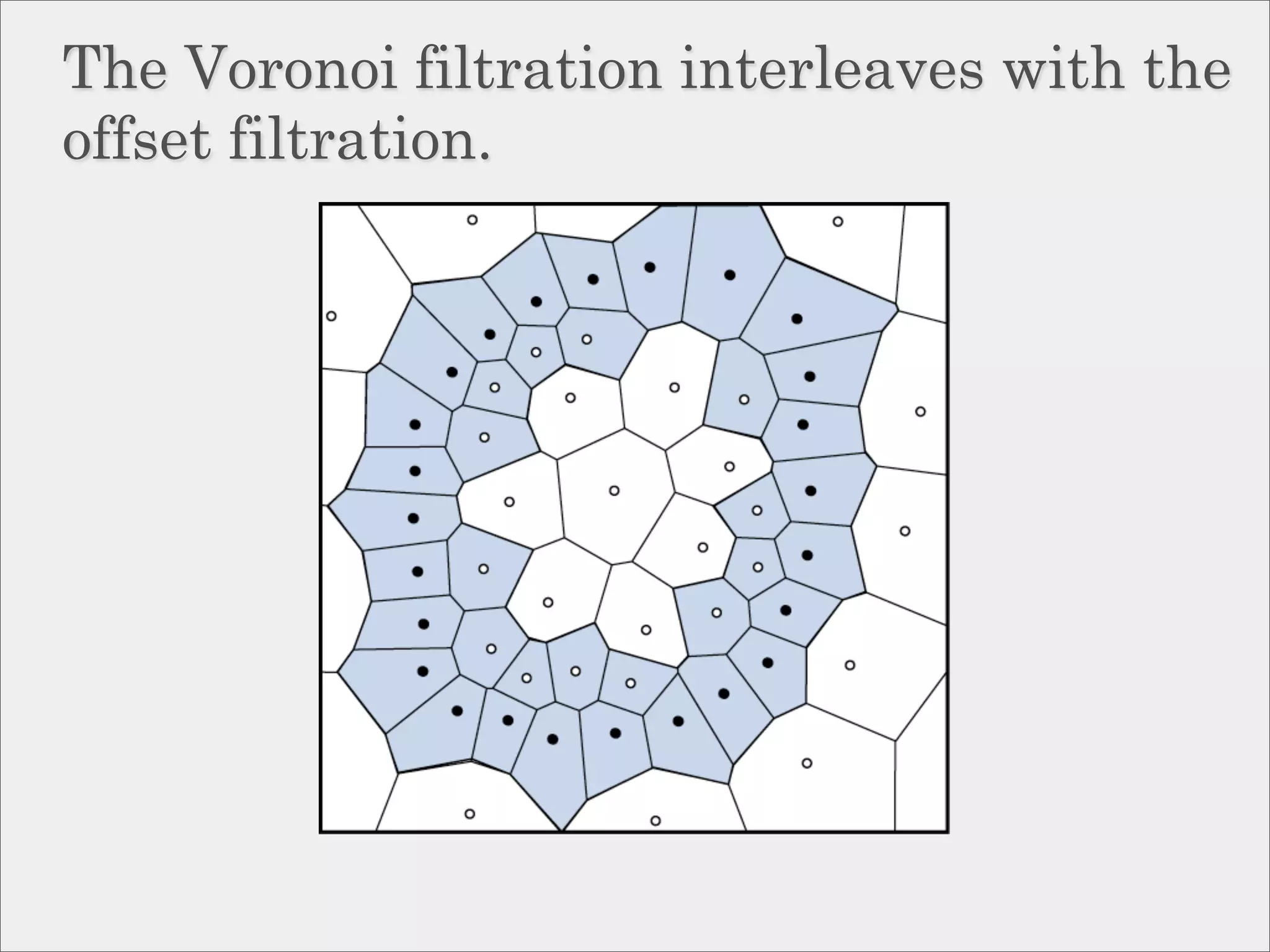
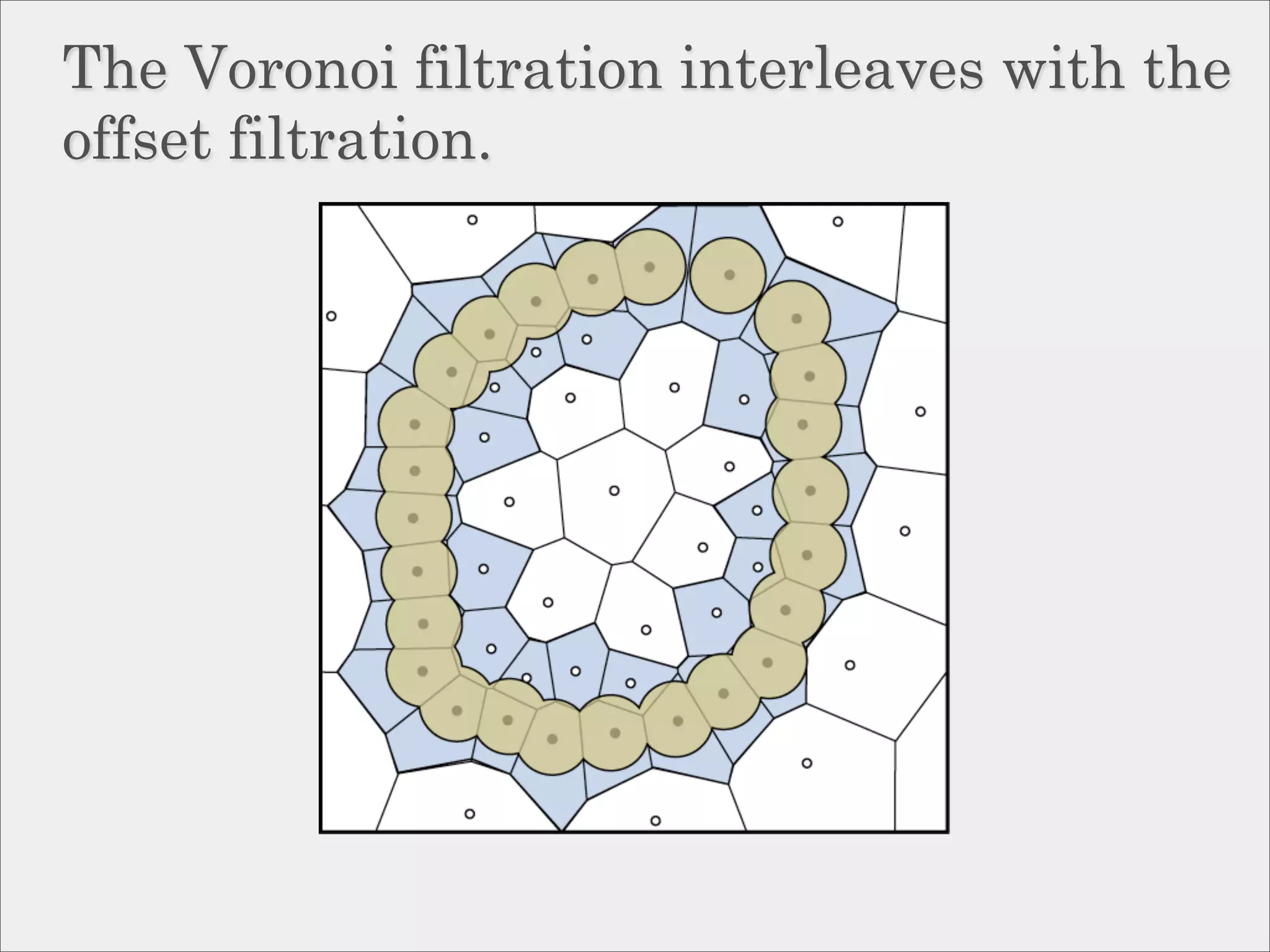
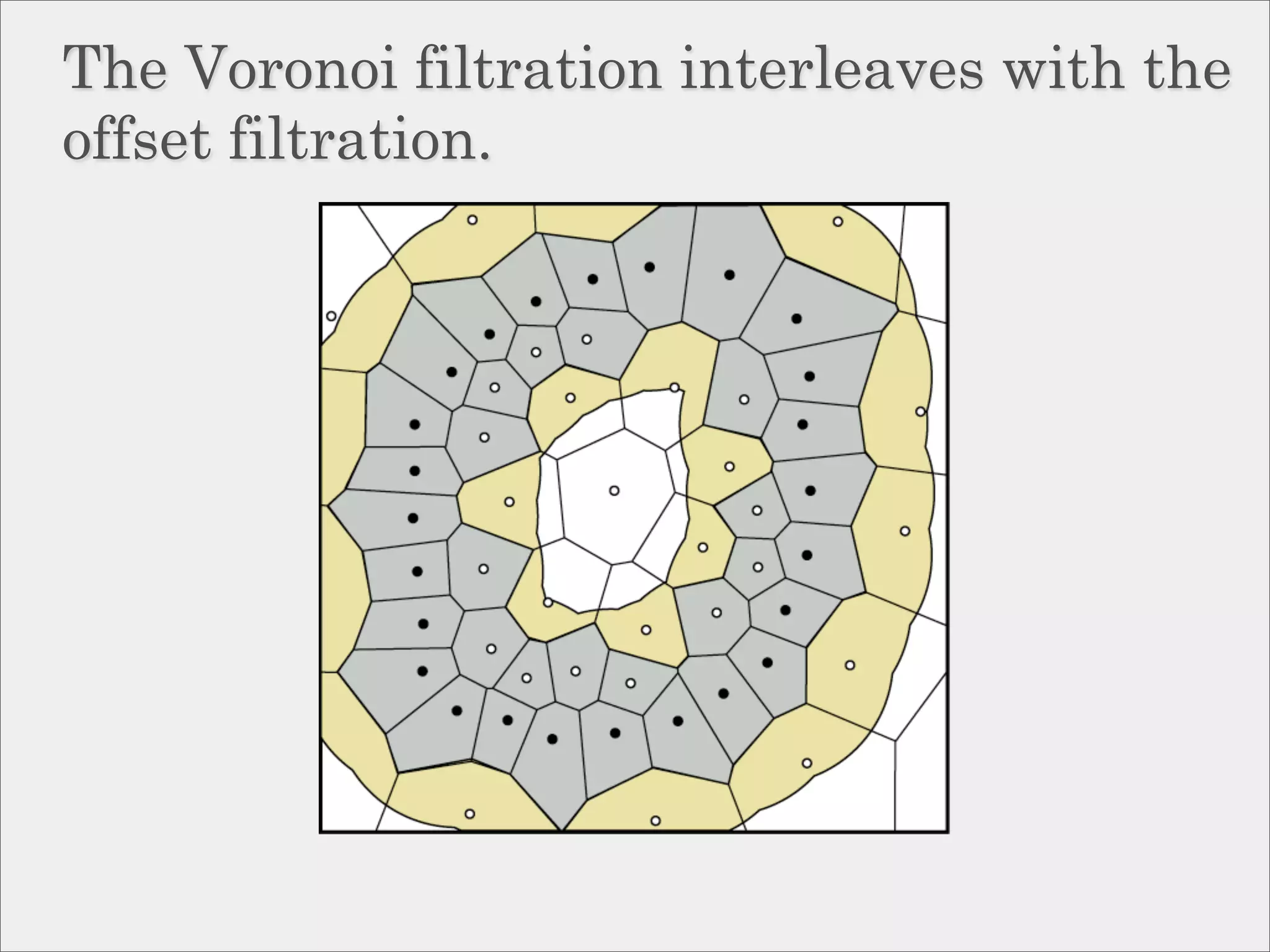
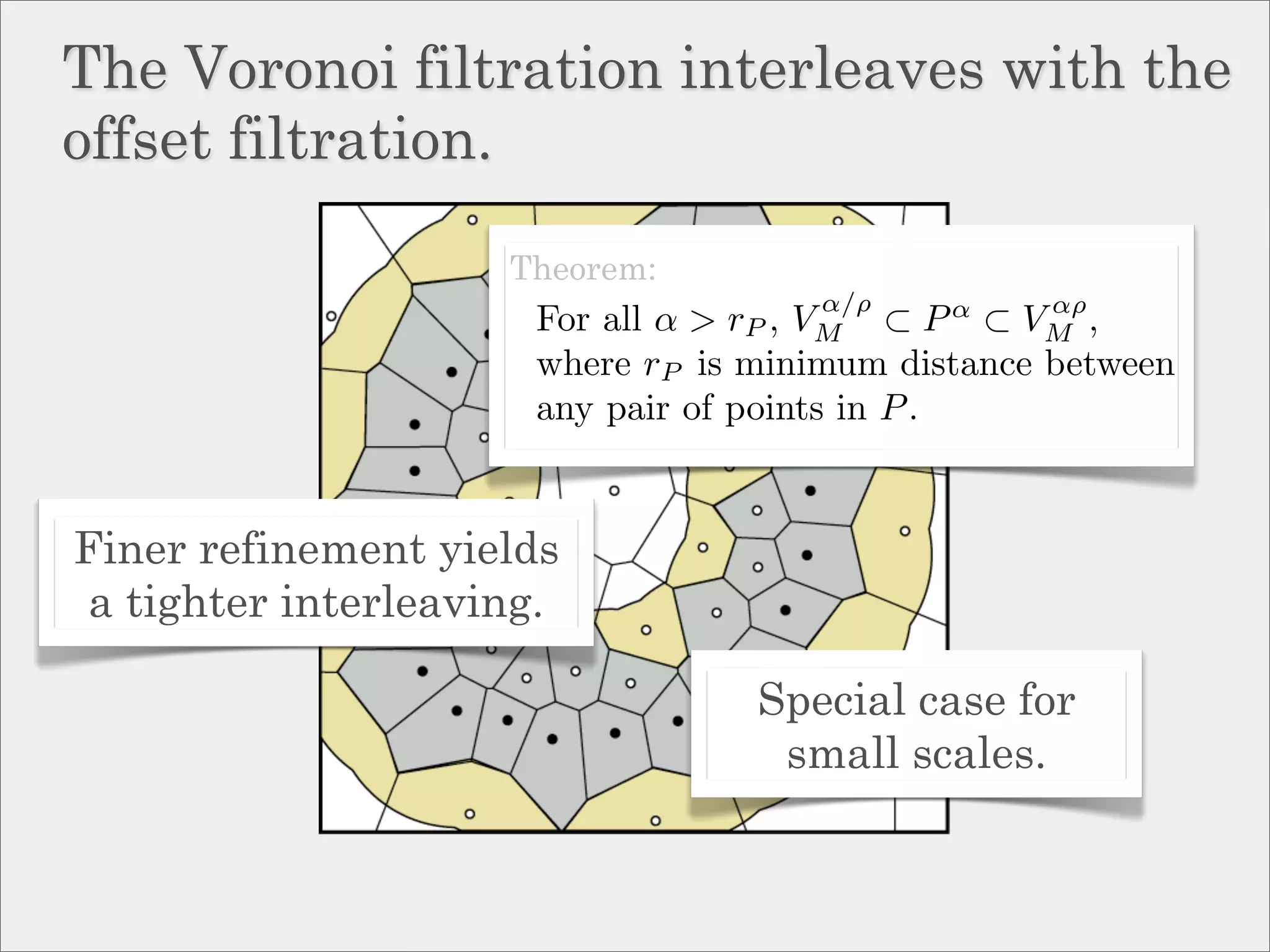
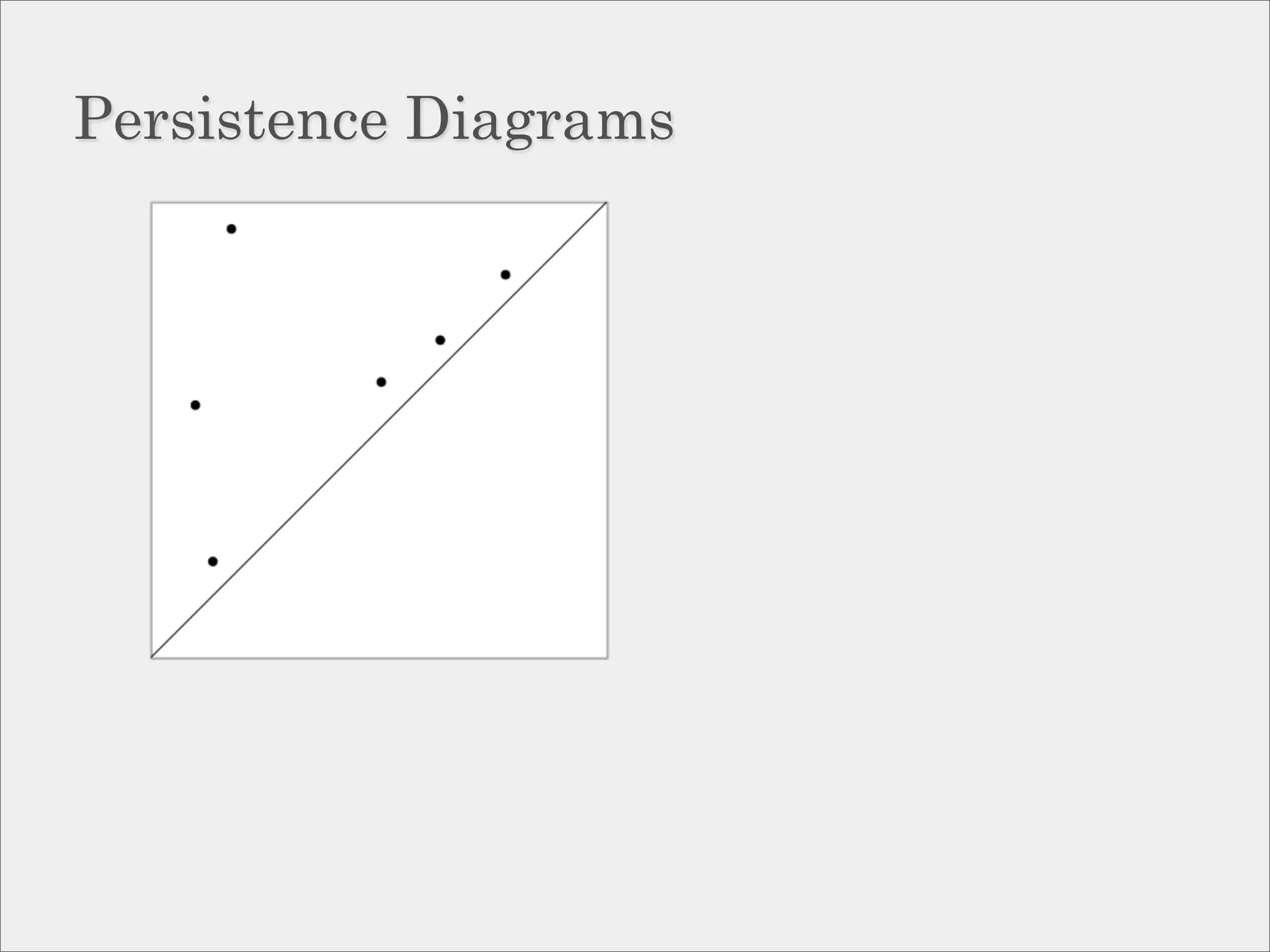
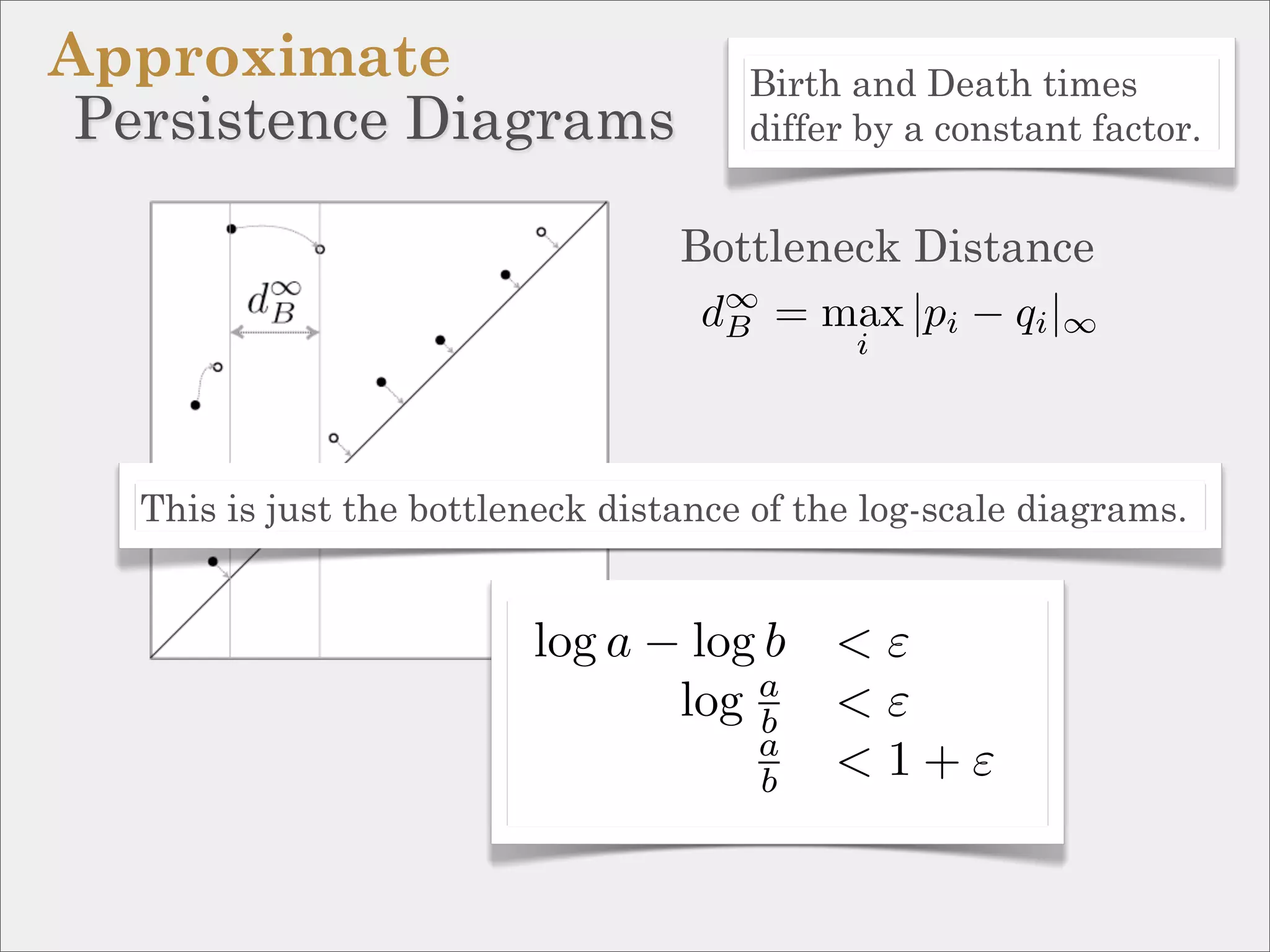
50. Approximation via interleaving.
Definition:
Two filtrations, {Pα } and {Qα } are
ε-interleaved if Pα−ε ⊆ Qα ⊆ Pα+ε
for all α.
Theorem [Chazal et al, ’09]:
If {Pα } and {Qα } are ε-interleaved then
their persistence diagrams are ε-close in
the bottleneck distance.

51. The Voronoi filtration interleaves with the
offset filtration.

52. The Voronoi filtration interleaves with the
offset filtration.

53. The Voronoi filtration interleaves with the
offset filtration.

54. The Voronoi filtration interleaves with the
offset filtration.

55. The Voronoi filtration interleaves with the
offset filtration.
Theorem:
α/ρ αρ
For all α > rP ,
VM ⊂ P α ⊂ VM ,
where rP is minimum distance between
any pair of points in P .

56. The Voronoi filtration interleaves with the
offset filtration.
Theorem:
α/ρ αρ
For all α > rP ,
VM ⊂ P α ⊂ VM ,
where rP is minimum distance between
any pair of points in P .
Finer refinement yields
a tighter interleaving.

57. The Voronoi filtration interleaves with the
offset filtration.
Theorem:
α/ρ αρ
For all α > rP ,
VM ⊂ P α ⊂ VM ,
where rP is minimum distance between
any pair of points in P .
Finer refinement yields
a tighter interleaving.
Special case for
small scales.

58. Geometric Topologically
Approximation Equivalent

59. Geometric Topologically
Approximation Equivalent

60. The Results Approximation ratio Complex Size
1. Build a mesh M. Previous
Work
1 nO(d)
2. Assign birth times to Simple
vertices based on distance to P mesh
filtration
(special case points very close
to P).**
Over-refine
3. For each simplex s of Del(M), the mesh
let birth(s) be the min birth
time of its vertices.
Linear-Size
4. Feed this filtered complex to Meshing
the persistence algorithm.

61. The Results Approximation ratio Complex Size
1. Build a mesh M. Previous
Work
1 nO(d)
2. Assign birth times to Simple
vertices based on distance to P mesh ρ 2 O(d2 )
n log ∆
filtration
(special case points very close
to P).**
Over-refine
3. For each simplex s of Del(M), the mesh
let birth(s) be the min birth
time of its vertices.
Linear-Size
4. Feed this filtered complex to Meshing
the persistence algorithm.

62. The Results Approximation ratio Complex Size
1. Build a mesh M. Previous
Work
1 nO(d)
2. Assign birth times to Simple
vertices based on distance to P mesh ρ =~3 2 O(d2 )
n log ∆
filtration
(special case points very close
to P).**
Over-refine
3. For each simplex s of Del(M), the mesh
let birth(s) be the min birth
time of its vertices.
Linear-Size
4. Feed this filtered complex to Meshing
the persistence algorithm.

63. The Results Approximation ratio Complex Size
1. Build a mesh M. Previous
Over-refine it. Work
1 nO(d)
2. Assign birth times to Simple
vertices based on distance to P mesh ρ =~3 2 O(d2 )
n log ∆
filtration
(special case points very close
to P).**
Over-refine −O(d2 )
1+ε n log ∆
3. For each simplex s of Del(M),
ε
the mesh
let birth(s) be the min birth
time of its vertices.
Linear-Size
4. Feed this filtered complex to Meshing
the persistence algorithm.

64. The Results Approximation ratio Complex Size
1. Build a mesh M. Previous
Over-refine it. Work
1 nO(d)
Use linear-size meshing.
2. Assign birth times to Simple
vertices based on distance to P mesh ρ =~3 2 O(d2 )
n log ∆
filtration
(special case points very close
to P).**
Over-refine −O(d2 )
1+ε n log ∆
3. For each simplex s of Del(M),
ε
the mesh
let birth(s) be the min birth
time of its vertices.
Linear-Size −O(d2 )
1 + ε + 3θ (εθ) n
4. Feed this filtered complex to Meshing
the persistence algorithm.

65. Thank you.