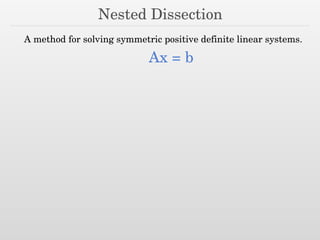
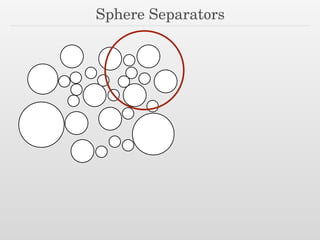
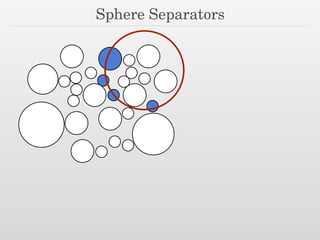
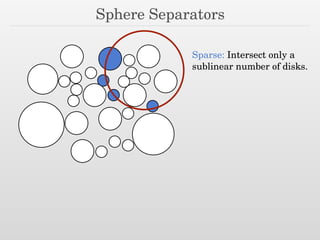
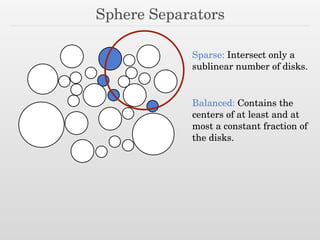
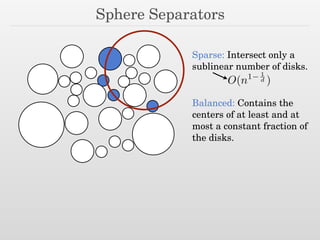
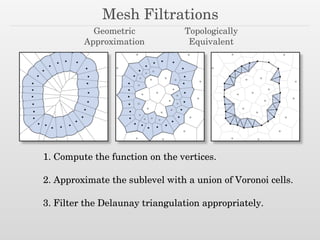
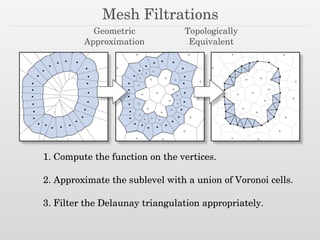
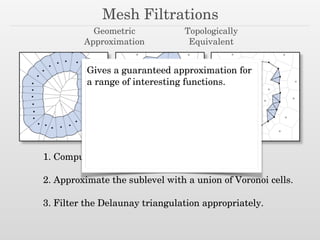
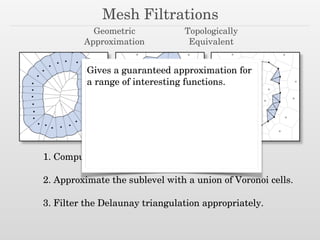
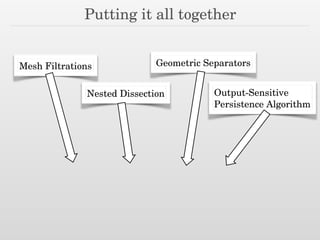
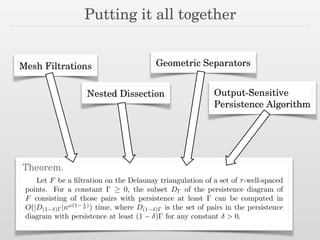
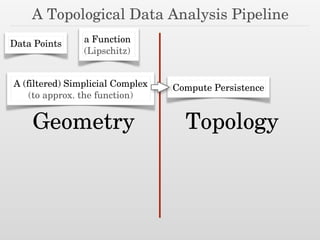
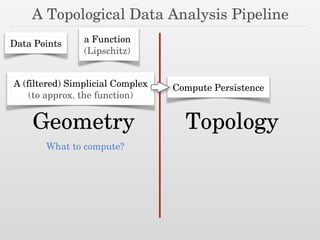
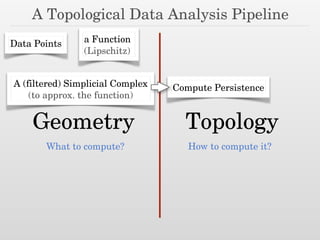
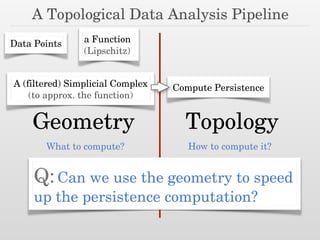
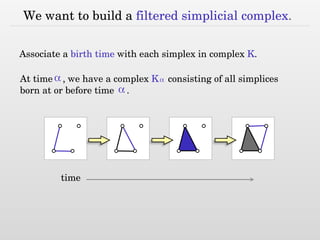
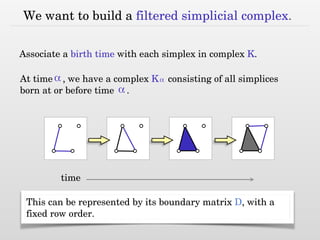
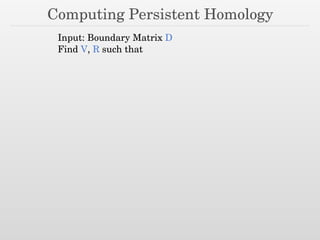
The document discusses using nested dissection and geometric separators to speed up computations of persistent homology. It proposes combining mesh filtrations, geometric separators, nested dissection, and output-sensitive persistence algorithms. This would allow beating the matrix multiplication time bound for computing persistent homology of functions defined on well-spaced point clouds. The technique exploits properties of meshes and separators to allow choosing a pivot order that improves the computation time.

1. Persistent Homology
and
Nested Dissection
Don Sheehy
University of Connecticut
!
joint work with Michael Kerber and Primoz Skraba

2. A Topological Data Analysis Pipeline

3. A Topological Data Analysis Pipeline
Data Points

4. A Topological Data Analysis Pipeline
Data Points a Function
(Lipschitz)

5. A Topological Data Analysis Pipeline
Data Points a Function
(Lipschitz)
A (filtered) Simplicial Complex
(to approx. the function)

6. A Topological Data Analysis Pipeline
Data Points a Function
(Lipschitz)
A (filtered) Simplicial Complex
(to approx. the function)
Compute Persistence

7. A Topological Data Analysis Pipeline
Data Points a Function
(Lipschitz)
A (filtered) Simplicial Complex
(to approx. the function)
Compute Persistence
Geometry

8. A Topological Data Analysis Pipeline
Data Points a Function
(Lipschitz)
A (filtered) Simplicial Complex
(to approx. the function)
Compute Persistence
Geometry Topology

9. A Topological Data Analysis Pipeline
Data Points a Function
(Lipschitz)
A (filtered) Simplicial Complex
(to approx. the function)
Compute Persistence
Geometry Topology
What to compute?

10. A Topological Data Analysis Pipeline
Data Points a Function
(Lipschitz)
A (filtered) Simplicial Complex
(to approx. the function)
Compute Persistence
Geometry Topology
What to compute? How to compute it?

11. A Topological Data Analysis Pipeline
Data Points a Function
(Lipschitz)
A (filtered) Simplicial Complex
(to approx. the function)
Compute Persistence
Geometry Topology
What to compute? How to compute it?
Q:Can we use the geometry to speed
up the persistence computation?

12. We want to build a filtered simplicial complex.
Associate a birth time with each simplex in complex K.
At timeα, we have a complex Kα consisting of all simplices
born at or before time α.
time

13. We want to build a filtered simplicial complex.
Associate a birth time with each simplex in complex K.
At timeα, we have a complex Kα consisting of all simplices
born at or before time α.
time
This can be represented by its boundary matrix D, with a
fixed row order.

14. Computing Persistent Homology

15. Computing Persistent Homology
Input: Boundary Matrix D
Find V, R such that

16. Computing Persistent Homology
Input: Boundary Matrix D
Find V, R such that
D = RV

17. Computing Persistent Homology
Input: Boundary Matrix D
Find V, R such that
D = RV
V is upper-triangular
R is “reduced” (i.e. no two columns
have lowest nonzeros in the same row)

18. Computing Persistent Homology
Input: Boundary Matrix D
Find V, R such that
D = RV
V is upper-triangular
R is “reduced” (i.e. no two columns
have lowest nonzeros in the same row)
Output is a collection of pairs corresponding
to the lowest nonzeros in R.

19. Computing Persistent Homology
Input: Boundary Matrix D
Find V, R such that
D = RV
V is upper-triangular
R is “reduced” (i.e. no two columns
have lowest nonzeros in the same row)
It’s just Gaussian elimination!
Output is a collection of pairs corresponding
to the lowest nonzeros in R.

20. The State of the Art
Asymptotics

21. The State of the Art
Asymptotics
“The Persistence Algorithm” [ELZ05] O(n3
)

22. The State of the Art
Asymptotics
“The Persistence Algorithm” [ELZ05]
via Matrix Multiplication [MMS11]
O(n3
)
O(n!
)

23. The State of the Art
Asymptotics
“The Persistence Algorithm” [ELZ05]
via Matrix Multiplication [MMS11]
Output-Sensitive [CK12] O(|D(1 ) |n2
)
O(n3
)
O(n!
)

24. The State of the Art
Asymptotics
Heuristics
“The Persistence Algorithm” [ELZ05]
via Matrix Multiplication [MMS11]
Output-Sensitive [CK12] O(|D(1 ) |n2
)
O(n3
)
O(n!
)

25. The State of the Art
Asymptotics
Heuristics
“The Persistence Algorithm” [ELZ05]
via Matrix Multiplication [MMS11]
Output-Sensitive [CK12]
Persistent Cohomology [MdSV-J11]
O(|D(1 ) |n2
)
O(n3
)
O(n!
)

26. The State of the Art
Asymptotics
Heuristics
“The Persistence Algorithm” [ELZ05]
via Matrix Multiplication [MMS11]
Output-Sensitive [CK12]
Persistent Cohomology [MdSV-J11]
Discrete Morse Reduction [MN13]
O(|D(1 ) |n2
)
O(n3
)
O(n!
)

27. The State of the Art
Asymptotics
Heuristics
“The Persistence Algorithm” [ELZ05]
via Matrix Multiplication [MMS11]
Output-Sensitive [CK12]
Persistent Cohomology [MdSV-J11]
Discrete Morse Reduction [MN13]
Clear and Compress [BKR13]
O(|D(1 ) |n2
)
O(n3
)
O(n!
)

28. Nested Dissection

29. Nested Dissection
A method for solving symmetric positive definite linear systems.

30. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b

31. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b
If A is n x n, consider the n vertex graph with an edge (i,j) for each
nonzero entry A(i, j) of A.

32. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b
If A is n x n, consider the n vertex graph with an edge (i,j) for each
nonzero entry A(i, j) of A.

33. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b
If A is n x n, consider the n vertex graph with an edge (i,j) for each
nonzero entry A(i, j) of A.
Find a vertex separator S such that

34. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b
If A is n x n, consider the n vertex graph with an edge (i,j) for each
nonzero entry A(i, j) of A.
Find a vertex separator S such that
- |S| = O(nβ
)

35. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b
If A is n x n, consider the n vertex graph with an edge (i,j) for each
nonzero entry A(i, j) of A.
Find a vertex separator S such that
- |S| = O(nβ
)
- each connected piece has O(n) vertices.

36. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b
If A is n x n, consider the n vertex graph with an edge (i,j) for each
nonzero entry A(i, j) of A.
Find a vertex separator S such that
- |S| = O(nβ
)
- each connected piece has O(n) vertices.
The Punchline:

37. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b
If A is n x n, consider the n vertex graph with an edge (i,j) for each
nonzero entry A(i, j) of A.
Find a vertex separator S such that
- |S| = O(nβ
)
- each connected piece has O(n) vertices.
The Punchline:
Inverting A can be done in O(nβω
) time.

38. Nested Dissection
A method for solving symmetric positive definite linear systems.
Ax = b
If A is n x n, consider the n vertex graph with an edge (i,j) for each
nonzero entry A(i, j) of A.
Find a vertex separator S such that
- |S| = O(nβ
)
- each connected piece has O(n) vertices.
The Punchline:
Inverting A can be done in O(nβω
) time.
Also works for computing ranks of singular,
nonsymmetric matrices over finite fields.

39. Sphere Separators

40. Sphere Separators

41. Sphere Separators

42. Sphere Separators
Sparse: Intersect only a
sublinear number of disks.

43. Sphere Separators
Sparse: Intersect only a
sublinear number of disks.
Balanced: Contains the
centers of at least and at
most a constant fraction of
the disks.

44. Sphere Separators
Sparse: Intersect only a
sublinear number of disks.
Balanced: Contains the
centers of at least and at
most a constant fraction of
the disks.
O(n1 1
d )

45. Sphere Separators
Sparse: Intersect only a
sublinear number of disks.
Balanced: Contains the
centers of at least and at
most a constant fraction of
the disks.
O(n1 1
d )
n
d + 2

46. Persistent Homology and Nested Dissection

47. Persistent Homology and Nested Dissection
A Conundrum:

48. Persistent Homology and Nested Dissection
A Conundrum:
Nested dissection gives an improvement by
choosing a good pivot order.

49. Persistent Homology and Nested Dissection
A Conundrum:
Nested dissection gives an improvement by
choosing a good pivot order.
Persistent homology restricts the pivot order.

50. Persistent Homology and Nested Dissection
A Conundrum:
Nested dissection gives an improvement by
choosing a good pivot order.
Persistent homology restricts the pivot order.

51. Persistent Homology and Nested Dissection
A Conundrum:
Nested dissection gives an improvement by
choosing a good pivot order.
Persistent homology restricts the pivot order.
The first trick:

52. Persistent Homology and Nested Dissection
A Conundrum:
Nested dissection gives an improvement by
choosing a good pivot order.
Persistent homology restricts the pivot order.
The first trick:
In the output-sensitive persistence algorithm of
Chen and Kerber, only ranks need to be computed.

53. Persistent Homology and Nested Dissection
A Conundrum:
Nested dissection gives an improvement by
choosing a good pivot order.
Persistent homology restricts the pivot order.
The first trick:
In the output-sensitive persistence algorithm of
Chen and Kerber, only ranks need to be computed.

54. Mesh Filtrations
Geometric
Approximation
Topologically
Equivalent
1. Compute the function on the vertices.
!
2. Approximate the sublevel with a union of Voronoi cells.
!
3. Filter the Delaunay triangulation appropriately.

55. Mesh Filtrations
Geometric
Approximation
Topologically
Equivalent
1. Compute the function on the vertices.
!
2. Approximate the sublevel with a union of Voronoi cells.
!
3. Filter the Delaunay triangulation appropriately.

56. Mesh Filtrations
Geometric
Approximation
Topologically
Equivalent
1. Compute the function on the vertices.
!
2. Approximate the sublevel with a union of Voronoi cells.
!
3. Filter the Delaunay triangulation appropriately.
Gives a guaranteed approximation for
a range of interesting functions.

57. Mesh Filtrations
Geometric
Approximation
Topologically
Equivalent
1. Compute the function on the vertices.
!
2. Approximate the sublevel with a union of Voronoi cells.
!
3. Filter the Delaunay triangulation appropriately.
Gives a guaranteed approximation for
a range of interesting functions.

58. Mesh Filtrations
Geometric
Approximation
Topologically
Equivalent
1. Compute the function on the vertices.
!
2. Approximate the sublevel with a union of Voronoi cells.
!
3. Filter the Delaunay triangulation appropriately.
Gives a guaranteed approximation for
a range of interesting functions.
Bonus: The theory of geometric
separators was invented for graphs
coming from meshes like this.

59. Putting it all together

60. Putting it all together
Mesh Filtrations Geometric Separators
Nested Dissection Output-Sensitive
Persistence Algorithm

61. Putting it all together
Mesh Filtrations Geometric Separators
Nested Dissection Output-Sensitive
Persistence Algorithm

62. Theorem.
Let F be a filtration on the Delaunay triangulation of a set of ⌧-well-spaced
points. For a constant 0, the subset D of the persistence diagram of
F consisting of those pairs with persistence at least can be computed in
O(|D(1 ) |n!(1 1
d )
) time, where D(1 ) is the set of pairs in the persistence
diagram with persistence at least (1 ) for any constant > 0.
Putting it all together
Mesh Filtrations Geometric Separators
Nested Dissection Output-Sensitive
Persistence Algorithm

63. Summary

64. Summary
We can beat the matrix multiplication bound
for computing the persistent homology of a wide
class of functions defined on quality meshes.

65. Summary
We can beat the matrix multiplication bound
for computing the persistent homology of a wide
class of functions defined on quality meshes.

66. Summary
We can beat the matrix multiplication bound
for computing the persistent homology of a wide
class of functions defined on quality meshes.
The main technique is a combination of recent
advances in nested dissection, persistence
computation, and geometric separators.

67. Summary
We can beat the matrix multiplication bound
for computing the persistent homology of a wide
class of functions defined on quality meshes.
The main technique is a combination of recent
advances in nested dissection, persistence
computation, and geometric separators.
Thanks.