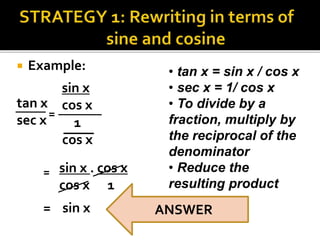
1. Simplifying trigonometric expressions may require trial and error but can be helped by using identities, writing functions in terms of sines and cosines, getting a common denominator, factoring, and breaking fractions. 2. An example problem is simplified by factoring out a common cos x term, using the identity cos^2 x = 1 - sin^2 x, and applying exponent properties to get the final expression of cos^3 x. 3. Strategies presented include using trigonometric identities to write functions in standard form, getting a common denominator, using trigonometric angle addition identities, and breaking fractions.

1. Code: STEM_PC11T-IIf-2

2.  Simplifying trigonometric expressions often takes
some trial and error, but the following strategies may
be helpful:
 Use algebra and fundamental identities to simplify the
expression.
 Sometimes, writing all functions in terms of sines and
cosines may help.
 Sometimes, combining fractions by getting a common
denominator may help.
 Sometimes, breaking one fraction into two fractions may
help: a+b/c = a/c + b/c
 Sometimes, factoring may help

3.  Example:
tan x
sec x=
= sin x . cos x
cos x 1
= sin x
sin x
cos x
1
cos x
• tan x = sin x / cos x
• sec x = 1/ cos x
• To divide by a
fraction, multiply by
the reciprocal of the
denominator
• Reduce the
resulting product
ANSWER

4.  Factor out a common factor of cos x
 Use the identity: cos2 x = 1-sin2 x
 Use a property of exponents to
multiply cos x and cos2 x
= cos x (1-sin2 x)
= cos x . cos2 x
= cos3 x
cos x – cos x sin2x
ANSWER

5. = sin x +cos x .
=
=
sin2 x + cos2 x
sin x sin x
cos x
sin x
• cot x = cos x / sin x
• Get a common
denominator of sin x
and add the two
fractions
• sin2 x + cos2 x =1
• csc x = 1/ sin x
sin2 x + cos2 x
sin x
1
sin x
csc x
=
=
sin x + cos x cot x
ANSWER

6. sec x – cos x
sec x
sec x
sec x
- cos x
sec x
=
= 1- cos2 x
= sin2 x
• a+b/c = a/c + b/c
• sec x divided by
itself is 1
• cos x/ sec x =
cos2 x
• 1- cos2 x = sin2 x
ANSWER

7.  SIMPLIFYING THE FOLLOWING:
1. CSC X –SIN X
CSC X
2. SIN X + COS X
COS X 1+ SIN X

8.  Give at least 3 examples of word problems
involving trigonometric expressions and
solutions. Write it in a whole sheet of paper
which will be submitted next meeting.
 Good bye class!

9. Code: STEM_PC11T-IIf-2