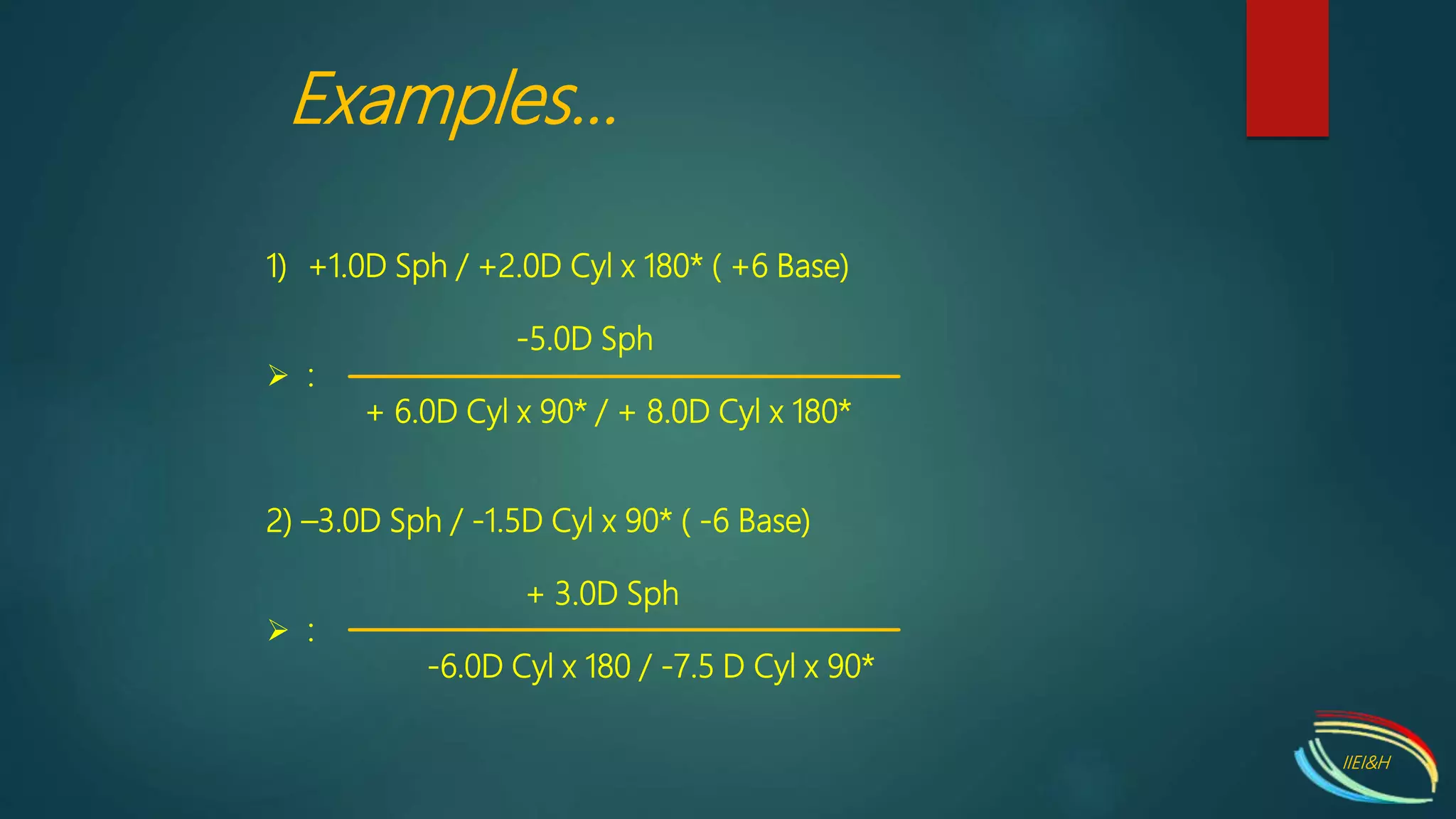The document discusses simple and toric transposition methods in optometry, outlining the process of changing lens power from positive to negative forms and vice versa. It includes rules and examples for calculating spherical and cylindrical powers through transposition. Additionally, it addresses finding spherical equivalents for correcting astigmatism using only spherical lenses.

1. Simple & Toric Transposition
Md: Azizul Islam, Junior Optometrist
Oculoplasty Department
Ispahani Islamia Eye Institute & Hospital
IIEI&H

2.  Transposition an application of changing the lens power
from one to another.
 Usually it is changed from ‘+’ form to ‘–‘ form.
Definition
Transposition two types :
1.Simple &
2.Toric Transposition
IIEI&H

3.  Algebric sum of sphere and cylinder ,To gate a new sphere.
 Cylindrical power will be same, but
 Sign and axis of cylinder will be in opposite ( 90 Degree apart angle).
 Examples:
 +2.5 D Sph / +3.0 D cyl x 150*
 a) + 5.5 D Sph
 b) 3.0 D cyl
 c) – cyl & 60*
 Final Rx : + 5.5D Sph / -3.0D Cyl x 60*
Rules –Simple transposition
IIEI&H

4. 1) -1.5 D Sph / -4.0 D Cyl x 105*
Answer : -5.5 D Sph / + 4.0D Cyl x 15*.
2) + 2.0 D Cyl x 90*
Answer : + 2.0 D Sph / -2.0D cyl x 180*
3) -1.5 D Sph / + 4.0 D Cyl x 105*
Answer : + 2.5 D Sph / -4.0 D Cyl x 15*
Few Examples
IIEI&H

5. Sphere into two cylinders.
+3.0D Sph = +3.0D cyl 90* / +3.0D cyl 180*
Cylinder into sphero-cylinder.
+3.0D cyl 90* = +3.0D Sph / -3.0D cyl 180*
Sphere-cylinder into
 Alternate Sphero-cylinder.
 Two cylinders.
Different Methods Of
Simple Transposition
IIEI&H

6.  Objective: To select the proper tools in cylinder lens surfacing.
 Rules:
 1.Choose the Base curve first for proper curvature.
 2.Do simple transposition if sign of base curve &cylinder not same.
 3.To find out the spherical surface power,
 Subtract the base curve from sphere.
 4.To find out the cylindrical surface power,
 Fix the Base curve at the right angle to the axis of cylinder.
 Add the base curve with cylinder
 5.Both spherical & cylindrical surface determines the lens power.
IIEI&H

7.  Example:
 + 1.0 D Sph / + 2.0 D Cyl x 165* (-6.0 Base curve)
 + 3.0 D Sph / -2.0D Cyl x 75*
 + 3.0 – ( -6.0) = + 9.0 D Sph.
 -6.0D Cyl x 165*
 -2.0 + ( -6.0) = -8.0D Cyl x 75*
+ 9.0D Sph
 :
-6.0D Cyl x 165*/ -8.0D Cyl x 75*
Toric Transposition
IIEI&H

8. 1) +1.0D Sph / +2.0D Cyl x 180* ( +6 Base)
-5.0D Sph
 :
+ 6.0D Cyl x 90* / + 8.0D Cyl x 180*
2) –3.0D Sph / -1.5D Cyl x 90* ( -6 Base)
+ 3.0D Sph
 :
-6.0D Cyl x 180 / -7.5 D Cyl x 90*
Examples...
IIEI&H

9.  Prescription -3.00/+5.00*90
Base curve -6.00
 First Step:
Transpose the prescription so that base
curve sign will be
similar to the base curve sign
 +2.00/-5.00*180
Example Review:
IIEI&H

10. Second Step:
Minus should be done between spherical and base curve power.
 -6.00 – (+2.00)
 -6.00 - 2.00
 -8.00
It will be used in a tool
Third Step:
Base curve axis will be completely perpendicular with the
prescription (which is transposed) So, axis will be
 -6.00*90
IIEI&H

11. Fourth Step:
Add Base curve and cylinder power
 -6.00 + (-5.00)*180
 -11.00*180
So, Final :
-8.00 Sph

-6.00 Cyl*90 / -11.00 Cyl*180
IIEI&H

12. A sphero-cylinder lens will correct for astigmatism and myopia or hyperopia. If it was
necessary to correct a nearsighted or farsighted person who also has astigmatism, but
there were no cylinder lenses available, what would be the best correction using only a
sphere lens.
How to Find the Spherical equivalent :
1. Take half the value of the cylinder and
2. Add it to the sphere power.
In other words, as a formula the spherical equivalent
Spherical Equivalent = Sphere + (Cylinder)/2
Example: +3.00 − 1.00 × 180º
spherical equivalent = +3.00 + (-1.00) /2 = +2.50D
Spherical Equivalent
IIEI&H

13. IIEI&H
IIEI&H