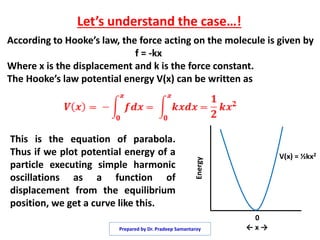
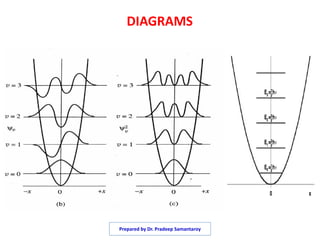
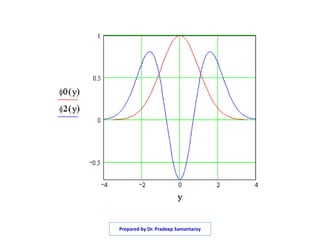
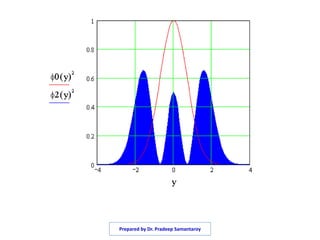
The document discusses the quantum mechanical treatment of the simple harmonic oscillator. It shows that the Schrodinger equation for a simple harmonic oscillator can be solved to obtain the Hermite equation. The solutions to the Hermite equation are the Hermite polynomials, which give the normalized wave functions and allowed energy levels of the simple harmonic oscillator. The energy levels are found to be quantized with energies equal to integer multiples of one half the angular frequency of oscillation.

1. Dr. Pradeep Samantaroy
Department of Chemistry
Rayagada Autonomous College, Rayagada
pksroy82@gmail.com; pksroy82@yahoo.in
9444078968

2. Oscillation
Periodic Variation
Any oscillation that can be expressed with a sinusoidal function is a harmonic
oscillation.
x(t) = x0 cos ( ωt + φ)
Where x0 is the amplitude
t is the time
ω is the angular frequency
φ is the phase angle
(ωt + φ) is the phase
The vibrational frequency of the oscillator of mass m is given by
For a diatomic molecule
Where µ is the reduced mass of diatomic molecule.
Prepared by Dr. Pradeep Samantaroy

3. Let’s understand the case…!
According to Hooke’s law, the force acting on the molecule is given by
f = -kx
Where x is the displacement and k is the force constant.
The Hooke’s law potential energy V(x) can be written as
This is the equation of parabola.
Thus if we plot potential energy of a
particle executing simple harmonic
oscillations as a function of
displacement from the equilibrium
position, we get a curve like this.
0
← x →
Energy
V(x) = ½kx2
Prepared by Dr. Pradeep Samantaroy

4. Let’s solve the case…!
Using the potential energy now the Schrodinger’s equation for the
one dimensional simple harmonic oscillator can be represented as
)()(
2
1
)(
2
2
2
22
xExkxx
dx
d
m
 





Mathematically this equation can be rearranged as
0
2
12 2
22
2






 

kxE
m
dx
d

Prepared by Dr. Pradeep Samantaroy

5. Let’s solve the case…!
The force constant in SHO is given by k = mω2
Substituting the value of k, the equation becomes
Defining a new variable ξ and a new parameter λ
0
2
12 22
22
2






 

xmE
m
dx
d

  xm
2/1
/   /2E
  02
2
2
 


d
d
Prepared by Dr. Pradeep Samantaroy

6. When ξ is very large λ-ξ2 ≈ -ξ2
So the equation becomes
02
2
2
 


d
d
 2/exp)( 2
 x
The solutions to the above equation are
Out of the two asymptotic solutions exp ξ2/2 is not acceptable
since it diverges when |ξ| →∞
Thus the exact solution can be written as
  )(.2/exp)( 2
 Hx 
Prepared by Dr. Pradeep Samantaroy

7. Substituting the solution the following equation,
The equation becomes
02
2
2
 


d
d
0)()1(
)(
2
)(
2
2
 





H
d
dH
d
Hd
This is the Hermite Equation and the solution will give Hermite
polynomials.
Prepared by Dr. Pradeep Samantaroy

8. n
n
naH  



0
)(
Substituting the above equation in previous equation
  0)12()2)(1(
0
2 



k
k
kk akakk 
kk a
kk
k
a
)2)(1(
12
2




When the coefficient of ξ is equated to zero we obtain the recurrence relation:
Prepared by Dr. Pradeep Samantaroy

9. The unnormalized wave function of one dimensional SHO is written as
Soving this the value of normalization constant will be
 .2/exp)()( 2
  nnn HN
2/12/1
)!(2
1















n
m
N nn



Prepared by Dr. Pradeep Samantaroy

10. ENERGY
The series can be terminated choosing λ in such a way that
(2k+1-λ) vanishes for k = n.
0)/(212  En  /2E







2
1
nEn
hnEn 






2
1
 2
Since
Since
n = 0,1,2,3,4…
Prepared by Dr. Pradeep Samantaroy

11. DIAGRAMS
Prepared by Dr. Pradeep Samantaroy

12. Prepared by Dr. Pradeep Samantaroy

13. Prepared by Dr. Pradeep Samantaroy