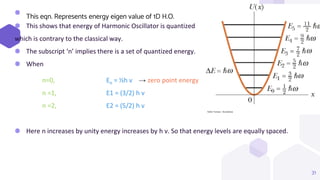
The document discusses the classical and quantum mechanical treatment of the simple harmonic oscillator. Classically, the simple harmonic oscillator exhibits sinusoidal motion with a single resonant frequency, where the restoring force is proportional to displacement from equilibrium. Quantum mechanically, the energy levels of the 1D harmonic oscillator are quantized and equally spaced. The wave functions are solutions of the Schrodinger equation and can be written as products of Hermite polynomials and Gaussian functions. The energy eigenstates of the 1D harmonic oscillator are (n+1/2)ħω, where n is the vibrational quantum number.

1. SIMPLE
HARMONIC
OSCILLATOR IN
CLASSICAL AND
QUANTUM
1D,2D,3D

2. Simple Harmonic Oscillator
1 Classical treatment

3. ⬢ Simple Harmonic Oscillator is a type of periodic motion where the restoring force on
the moving object is directly proportional to the magnitude of the object's displacement
and acts towards the object's equilibrium position.
⬢ It results in an oscillation which, if uninhibited by friction or any
other dissipation of energy, continues indefinitely.
⬢ The motion is sinusoidal in time and demonstrates a single resonant frequency.
⬢ Other phenomena can be modeled by simple harmonic motion, including the motion of
a simple pendulum.
3

4. ⬢ The uppermost mass m feels a force acting to the right
equal to k x, where k is Hooke's spring constant (a positive
number). The mass in the middle is in equilibrium, and the
mass at the bottom feels a force to the left equal to −k x.
The force executed by the springs always acts so as to
restore the mass back toward its equilibrium position. If
the mass is pulled out of equilibrium to x = A and then let
go, the mass will (in an ideal setup) oscillate forever
between ±A.
4

5. 5
The motion of the mass (the blue ball in figure 1) as a function of
time t may be obtained from Newton's second law (F = ma).
Bringing the force F and the acceleration a (times mass m) to the
same side of Newton's equation, the harmonic oscillator equation
becomes the following equation on the left:

6. 6
We see that the second derivative of x is proportional to −x. So the
equation for wave function becomes;.

7. ⬢ Substitution into the harmonic oscillator equation gives
⬢ when the phase angle φ is zero:

8. ⬢ The speed of the mass is the first derivative of position with respect to
time,
Which for the specific values of time becomes
8

9. ⬢ From classical mechanics it is known that the potential energy is minus the force
integrated over distance:
⬢ where the zero of the potential is at the arbitrary point x0 (the lower limit of the
integral). Upon choosing x0 = 0, we find V(x0) = 0, so that V(x) = (k/2)x2.
⬢ Introducing a minor generalization, we shift the origin on the x-axis from 0 to the
arbitrary point x0, i.e. we make the substitution x → x−x0. Then the harmonic potential
becomes the following quadratic function in the displacement x − x0,
9

10. ⬢ It is of interest to show the connection with the Taylor expansion of an arbitrary
potential around x0
⬢ The expansion is truncated after these three terms. Take V(x0) as zero of potential
and assume that x0 is a stationary point of the potential, i.e., that the potential at x0
has a minimum, a maximum, or a point of inflection (saddle point). This means that
we assume that
⬢ Then the truncated Taylor series shrinks to
⬢ If Hooke's (spring) constant is identified thus:
10

11. ⬢ we have found the harmonic potential from the truncated Taylor series.
⬢ The derivation went from the force to the potential by integrating over distance.
Conversely, given a potential V,corresponding force F is minus the derivative V’,
⬢ So, one could say that Hooke's law (force linear in displacement) is proved by use of a
truncated Taylor expansion.
11

12. ⬢ ENERGY
⬢ The oscillating mass has kinetic plus potential energy:
⬢ Above it was shown that
12

13. ⬢ So that,
⬢ where it was used that ω2 = k/m and cos2 + sin2 = 1. Hence, the total energy of the
harmonic oscillator is constant (independent of time). It is quadratic in the
amplitude A and proportional to the spring constant k. The stiffer the string the more
energy.
13

14. Quantum Harmonic Oscillator
2 1D

15. Quantum Mechanical Treatment
-One Dimensional Simple Harmonic Oscillator
We can write Schrodinger wave equation as;
ĤΨ= EΨ
Where Ĥ is the total energy operator
That is we can write,
Ĥ = (KE+PE)
In the case of SHO the P.E V is,
V = 1/2 ( k x ²)
The frequency of oscillation
ν = 1/(2 π) (k/m)½
15

16. Therefore,
k = 4π²ν²m (k= force constant)
Substitute k in V;
V= 2π²ν²mx²
This value is the P.E operator
K.E operator is given by,
ˆE =-(h²/8π²m)(d²/dx²)
Therefore, the Hamiltonian operator for a Harmonic Oscillator is given by;
Ĥ = -((h²/8π²m)(d²/dx²)) + 2π²ν²mx²
(m = mass x = displacement ν = frequency of oscillation)
16

17. ⬢ Thus the Schrodinger equation ĤΨ= EΨ for such a motion can be written as;
-((h²/8π²m)(d²Ψ/dx²)) + 2π²ν²mx²Ψ=EΨ
d²Ψ/dx² + [(8π²m(E -2π²ν²mx²))/h²]Ψ=0 ....(1)
d²Ψ/dx² + [8π²mE/h²-(16 π⁴m²ν²/h²)x²]Ψ=0 ....(2)
⬢ Let α = 8π²mE/h² ; β = 4π²mν/h
Therefore ; eqn.(2) gives,
d²Ψ/dx²+ [α- β²x²]Ψ = 0 ....(3)
17

18. ⬢ This eqn. can be solved subject to the following boundary conditions;
As x → ± ∞ ; Ψ → 0
⬢ In order to apply the boundary conditions we make the following change of
variables
Let y = (√ β)x
x =y/√ β dx = dy/√ β
d²Ψ/dx² = β d²Ψ/dy²
Substituting this values in eqn.(3) we get
β d²Ψ/dy² + [ α- (β²y²)/ β] Ψ = 0
That is;
d²Ψ/dy² + [α/β - y²] Ψ = 0 ....(4)
18

19. ⬢ This eqn. is purely algebraic form.
⬢ Now we can find the solution for this eqn
SOLUTION:
⬢ An asymptotic solution can be obtained for a very large values of y.
⬢ [Asymptotic solution means if the independent value tends to infinity the
dependent value or its derivative tends to a constant value.
For eg:
y = 2+ 1/x → tends to asymptotic value of 2 as x tends to infinity
⬢ Similarly here we can obtain an asymptotic solution for a very large solution of y,
⬢ So when y >> α/β ; Eqn.(4) reduces to
d²Ψ/dy² - y² Ψ = 0 ....(5)
19

20. ⬢ The solution of this eqn. is ;
Ψ = e ± y²/2
Proof;
[d²Ψ/dy² = d²e± y²/2/dy²
= y²e± y²/2 ± e± y²/2
= (y²± 1)e± y²/2
⬢ For every large values of y;
y²+1 = y (approximately)
d²Ψ/dy² = y² e± y²/2 = y² Ψ .... Hence proved ]
We have 2 solutions, either Ψ = e+y²/2 and Ψ = e-y²/2
20

21. ⬢ Since e+y²/2 is not acceptable, Because in that case Ψ → ∞ as y → ± ∞
⬢ Therefore the solution e-y²/2 which satisfies the boundary condition is the one valid
for large values of y.
⬢ Ψ = e-y²/2 is an asymptotic solution of eqn. (4).
Therefore the general solution of eqn.(4) contains the factor e-y²/2 and we assume
that the complete solution of eqn.(4) is of the form;
Ψ = F(y) e-y²/2 ....(6)
⬢ F(y) can be determined by finding its differential eqn.
dΨ/dy = F(y)( -2ye-y²/2/2 ) + e-y²/2dF/dy
d²Ψ/dy²=e-y²/2[d²F/dy²-2ydF/dy+(y²-1)F(y)] ....(7)
21

22. ⬢ Substituting in eqn.(4)
e-y²/2[d²F/dy²-2ydF/dy +(y²-1)F(y)]+ [α/β - y²] F(y) e-y²/2 = 0
Taking e-y²/2 as common,
e-y²/2[d²F/dy²-2ydF/dy+((α/β)–1)F(y)] = 0
Here the exponential part cannot be zero. It should always +ve,
Therefore,
[d²F/dy² - 2ydF/dy + ((α/β) – 1)F(y)]= 0. ...(8)
This is the differential eqn. for F(y) and is known as Hermite's differential eqn.
This eqn. can be solved by polynomial method, function F can be expanded as a power
series in y.
22

23. F = a0 + a1y + a2y² + a3y³ + a4y⁴ + ......(a)
dF/dy = a1 + 2a2y + 3a3y² + 4a4y³ + .....(b)
d²F/dy² = (1.2)a2 + (2.3)a3y + (3.4)a4y²+ ....(c)
Substituting (a),(b),(c) in eqn.(8) we get,
[((1.2)a2 + (2.3)a3y + (3.4)a4y² +....) – (2 a1y + 4a2y² + 6a3y³ +.....) + ((α/β) – 1)a0 + (α/β) – 1)a1y
+ (α/β) – 1)a2y² + ......)] = 0
⬢ This eqn. can be satisfied only if the coefficient of each power of y is 0.
That is,
For y⁰;
(1.2)a2+ (α/β) – 1)a0 = 0 23

24. ⬢ For y²;
(3.4)a4 + [(α/β)– 1) –(2.2)]a2 = 0
.... ... .... ..... .... ... .... ..... .....
..... .... ... ..... .... ... .. ... .......
For yk;
(k+1)(k+2)ak+2+[(α/β)-1-2k]ak=0
⬢ Therefore,
ak+2 = -[((α/β) – 1-2k)ak]/[(k+1)(k+2)] ...(9)
Where k is an integer
⬢ This eqn. is known as Recursion formula.
⬢ It permits the calculation of the coefficient ak+2 of the term yk+2 in terms of the
coefficient ak of yk.
24

25. Quantum Harmonic Oscillator
3 Wave function
1D

26. Harmonic Oscillator Wave function is given by;
Ψ = F(y) e-y²/2
⬢ The power series consists of infinite terms and the function
F(y)→ ∞ as y → ∞
⬢ That is the behaviour of power series for large values of y is unacceptable. So to
avoid the difficulty we have to restrict the number of terms in the series.
⬢ That is terminate the series after a certain number of terms. So that we’ve a
polynomial solution instead of power series. This is possible for a certain values of
k say n, the numerator in eqn.(9) vanishes
26

27. ⬢ That is,
(α/β) – 1- 2k = (α/β) – 1- 2n =0
or
α/β = 2n+1 (α = β(2n+1) n= 0,1,2,3,...)
⬢ The resulting series with finite number of terms is a polynomial called Hermite
Polynomial Hn(y).
⬢ The Hermite Polynomial are defined by the “generating function".
Hn(y) = (-1)ney²dn(e-y²)/dyn → obtained from recursion formula
⬢ The Harmonic Oscillator Wave function now becomes:
Ψn(y) = Hn(y) e-y²/2
This eqn. is the eigen function of 1 D Harmonic Oscillator
27

28. 28

29. Quantum Harmonic Oscillator
4 Energy eigen value
1D

30. Energy Eigen Values of Harmonic Oscillator
From the recursion formula we got
α = β(2n+1) ....(1)
We know that
α = 8π²mE/h² ; β = 4π²mν/h
Substituting α and β in (1) we get,
8π²mE/h² = 4π²mν(2n+1)/h
Therefore,
E = (2n+1)hν/2
En = (n + ½) hν (n =0,1,2,3...)
h= plank’s constant ν= frequency of oscillation En = Vibrational energy
n= Vibrational quantum number 30

31. ⬢
⬢ This shows that energy of Harmonic Oscillator is quantized
which is contrary to the classical way.
⬢ The subscript ‘n’ implies there is a set of quantized energy.
⬢ When
n=0, Eo = ½h ν → zero point energy
n =1, E1 = (3/2) h ν
n =2, E2 = (5/2) h ν
⬢ Here n increases by unity energy increases by h ν. So that energy levels are equally spaced.
31
This eqn. Represents energy eigen value of 1D H.O.

32. ⬢ Finding Normalization Constant
32
Expressing in terms of Ψ

33. 33
Normalisation constant
Ψn(y) = Nn Hn(y) e-y²/2
Ψn(y) = (√β/2nn! √π)1/2Hn(y) e-y²/2
This is the eigen function of 1D SHO

34. Quantum Harmonic Oscillator
5 2D

35. Wave function
The potential in 2D harmonic oscillator
𝑽 𝒙, 𝒚 =
𝟏
𝟐
𝒎𝝎𝒙
𝟐
𝒙𝟐
+
𝟏
𝟐
𝒎𝝎𝒚
𝟐
𝒚𝟐
In terms of Schrödinger’s equation:
ℏ𝟐
𝟐𝒎
𝝏𝟐
𝝏𝒙𝟐 +
𝝏𝟐
𝝏𝒚𝟐 𝜳 𝒙, 𝒚 + 𝑽 𝒙, 𝒚 𝜳 𝒙, 𝒚 = 𝑬𝜳(𝒙, 𝒚)
Substituting the two-dimension potential, V(x, y,), gives you this equation:
−
ℏ𝟐
𝟐𝒎
𝝏𝟐
𝝏𝒙𝟐 +
𝝏𝟐
𝝏𝒚𝟐 𝜳 𝒙, 𝒚 + (
𝟏
𝟐
𝒎𝝎𝒙
𝟐
𝒙𝟐
+
𝟏
𝟐
𝒎𝝎𝒚
𝟐
𝒚𝟐
)𝜳 𝒙, 𝒚 = 𝑬𝜳(𝒙, 𝒚)

36. ⬢ Using separable theorem, we can write the above equation in terms
of x and y coordinate
𝜳 𝒙, 𝒚 = 𝑿 𝒙 𝒀(𝒚)
⬢ Therefore, the Schrödinger equation in x and y terms will be:
−
ℏ𝟐
𝟐𝒎
𝝏𝟐
𝝏𝒙𝟐 𝑿 𝒙 + (
𝟏
𝟐
𝒎𝝎𝒙
𝟐
𝒙𝟐
)𝑿 𝒙 = 𝑬𝒙𝑿(𝒙)
−
ℏ𝟐
𝟐𝒎
𝝏𝟐
𝝏𝒚𝟐 𝒀 𝒚 + (
𝟏
𝟐
𝒎𝝎𝒚
𝟐
𝒚𝟐
)𝒀 𝒚 = 𝑬𝒚𝒀(𝒚)
Solving the equations we get this as the solution
𝜳 𝒙, 𝒚 =
𝒂𝒙
𝟐𝒏𝒙𝒏𝒙! 𝝅
𝟏
𝟐
𝑯𝒏𝒙 𝟐𝒏𝒙 𝒆
−𝜶𝒙𝟐
𝟐
𝒂𝒚
𝟐𝒏𝒚𝒏𝒚! 𝝅
𝟏
𝟐
𝑯𝒏𝒚 𝟐𝒏𝒚 𝒆
−𝜶𝒚𝟐
𝟐

37. Energy
The Hamiltonian for 2D harmonic oscillator is
𝐻 =
𝑝𝑥
2+ 𝑝𝑦
2
2𝑚
+
1
2
𝑚𝜔2 𝑥2 + 𝑦2 ……….for isotropic harmonic oscillator
𝐻 =
𝑝𝑥
2+ 𝑝𝑦
2
2𝑚
+
1
2
𝑚 𝜔𝑥
2
𝑥2
+ 𝜔𝑦
2
𝑦2
……….for anistropic harmonic oscillator
By solving 𝐻Ψ = 𝐸Ψ , we can get the energy eigenvalues in terms of x and y
𝑬𝒏𝒙+ 𝒏𝒚
= 𝒏𝒙 +
𝟏
𝟐
ℏ𝝎𝒙 + 𝒏𝒚 +
𝟏
𝟐
ℏ𝝎𝒚

38. For isotropic harmonic oscillator 𝜔 is same in all directions
(𝜔𝑥= 𝜔𝑦 = 𝜔)
𝑬𝒏𝒙+ 𝒏𝒚
= 𝒏𝒙 + 𝒏𝒚 + 𝟏 ℏ𝝎
For anisotropic harmonic oscillator 𝜔 is different in all directions
𝜔𝑥 ≠ 𝜔𝑦 or 𝜔𝑥 > 𝜔𝑦
𝑬𝒏𝒙+𝒏𝒚
= 𝒏𝒙 +
𝟏
𝟐
ℏ𝝎𝒙 + 𝒏𝒚 +
𝟏
𝟐
ℏ𝝎𝒚
38

39. Degeneracy
For isotropic harmonic oscillator, the energy term is
𝑬𝒏𝒙+ 𝒏𝒚
= 𝒏𝒙 + 𝒏𝒚 + 𝟏 ℏ𝝎 [𝑛 = 𝑛𝑥 + 𝑛𝑦]
The energy eigenvalue becomes, 𝑬𝒏 = 𝒏 + 𝟏 ℏ𝝎
⬢ 𝑛 = 0 ⟶ 𝑛𝑥= 0; 𝑛𝑦 = 0 ……no degeneracy
⬢ 𝑛 = 1 ⟶ (𝑛𝑥 = 1; 𝑛𝑦= 0) (𝑛𝑥 = 0; 𝑛𝑦 = 1) …….2 degenerate states
Similarly for n=2 we get three degenerate states
⬢ For 𝑛𝑡ℎ
excited state there will be (n+1) degenerate states.

40. Quantum
number(n)
Energy
[𝐸𝑛 = 𝑛 + 1 ℏ𝜔]
Combinations
(𝑛𝑥 , 𝑛𝑦)
Number of
degenerate
states
n = 0 ℏ𝜔 (0,0) 1
n = 1 2ℏ𝜔 (1,0) (0,1) 2
n = 2 3ℏ𝜔 (2,0) (0,2) (1,1) 3
.
.
.
.
n (n+1) ℏ𝜔 (n,0) (n-1, 0)
(n-2, 0)……(0,n)
(n+1)
For 2D isotropic harmonic oscillator

41. For anisotropic harmonic oscillator, the energy term is
𝑬𝒏𝒙+𝒏𝒚
= 𝒏𝒙 +
𝟏
𝟐
ℏ𝝎𝒙 + 𝒏𝒚 +
𝟏
𝟐
ℏ𝝎𝒚
Quantum
number(n)
Combination
s
(𝑛𝑥 , 𝑛𝑦)
Energy
(𝐸𝑛)
n = 0 (0,0) ℏ 𝜔1 + 𝜔2
2
n = 1 (0,1) ℏ𝜔1
2
+
3ℏ𝜔2
2
(1,0) 3ℏ𝜔1
2
+
ℏ𝜔2
2
The energies are not
same
There is no degeneracy in 2D anisotropic harmonic oscillator.

42. SIMULATION LINK FOR 2-D HARMONIC
OSCILLATOR
https://www.st-
andrews.ac.uk/physics/quvis/simulations_html5/sims/QuantumOscillator/oscillator2.h
~:text=A%20classical%20particle%20has%20a,beyond%20the%20classical%20turn
0points
42

43. Quantum Harmonic Oscillator
6 3D

44. Wave function
⬢ Now take a look at the harmonic oscillator in three
dimensions. In three dimensions, the potential looks
like this:
Schrödinger’s equation:
44
−
ℏ𝟐
𝟐𝒎
𝝏𝟐
𝝏𝒙𝟐
+
𝝏𝟐
𝝏𝒚𝟐
+
𝝏𝟐
𝝏𝒛𝟐
𝜳 𝒙, 𝒚, 𝒛 + 𝑽(𝒙, 𝒚, 𝒛)𝜳 𝒙, 𝒚, 𝒛 = 𝑬𝜳(𝒙, 𝒚, 𝒛)

45. ⬢ Substituting in for the three-dimension potential, V(x, y, z), gives you this
equation
−
ℏ𝟐
𝟐𝒎
𝝏𝟐
𝝏𝒙𝟐
+
𝝏𝟐
𝝏𝒚𝟐
+
𝝏𝟐
𝝏𝒛𝟐
𝜳 𝒙, 𝒚, 𝒛 + (
𝟏
𝟐
𝒎𝝎𝒙
𝟐𝒙𝟐 +
𝟏
𝟐
𝒎𝝎𝒚
𝟐𝒚𝟐
+
𝟏
𝟐
𝒎𝝎𝒛
𝟐𝒛𝟐)𝜳 𝒙, 𝒚, 𝒛 = 𝑬𝜳(𝒙, 𝒚, 𝒛)
⬢ Using separable theorem, we can write the above equation in terms of x
y and z coordinate
𝜳 𝒙, 𝒚, 𝒛 = 𝑿 𝒙 𝒀 𝒚 𝒁(𝒛)

46. ⬢ Therefore, the Schrödinger equation looks like this for x:
⬢ Solving that equation, you get this next solution:
where
and nx = 0, 1, 2, and so on. The Hnx term indicates a Hermite polynomial.
Therefore the wave function is
𝜳 𝒙, 𝒚, 𝒛 =
𝟏
𝝅
𝟑
𝟒
𝟏
𝟐𝒏𝒙+𝒏𝒚+𝒏𝒛𝒏𝒙! 𝒏𝒚! 𝒏𝒛!
𝟏
𝟐
𝑯𝒏𝒙
𝒙
𝒙𝟎
𝑯𝒏𝒚
𝒚
𝒚𝟎
𝑯𝒏𝒛
𝒛
𝒛𝟎
𝒆
−
𝒙𝟐
𝟐𝒙𝟎
𝟐 −
𝒚𝟐
𝟐𝒚𝟎
𝟐 −
𝒛𝟐
𝟐𝒛𝟎
𝟐

47. Energy
⬢ The energy eigenvalues in terms of x, y and z
𝑬𝒏𝒙+ 𝒏𝒚+𝒏𝒛
= 𝒏𝒙 +
𝟏
𝟐
ℏ𝝎𝒙 + 𝒏𝒚 +
𝟏
𝟐
ℏ𝝎𝒚+ 𝒏𝒛 +
𝟏
𝟐
ℏ𝝎𝒛
For isotropic harmonic oscillator 𝜔 is same in all directions (𝜔𝑥=
𝜔𝑦 = 𝜔𝑧 = 𝜔)
𝑬𝒏𝒙+ 𝒏𝒚+𝒏𝒛
= 𝒏𝒙 + 𝒏𝒚 + 𝒏𝒛 +
𝟑
𝟐
ℏ𝝎
For anisotropic harmonic oscillator 𝜔 is different in all directions
𝜔𝑥 ≠ 𝜔𝑦 ≠ 𝜔𝑧
𝑬𝒏𝒙+𝒏𝒚+𝒏𝒛
= 𝒏𝒙 +
𝟏
𝟐
ℏ𝝎𝒙 + 𝒏𝒚 +
𝟏
𝟐
ℏ𝝎𝒚 + 𝒏𝒛 +
𝟏
𝟐
ℏ𝝎𝒛

48. Degeneracy
For isotropic harmonic oscillator, the energy term is
𝑬𝒏𝒙+ 𝒏𝒚+𝒏𝒛
= 𝒏𝒙 + 𝒏𝒚 + 𝒏𝒛 +
𝟑
𝟐
ℏ𝝎 [𝑛 = 𝑛𝑥 + 𝑛𝑦 + 𝑛𝑧]
The energy eigenvalue becomes, 𝑬𝒏 = 𝒏 +
𝟑
𝟐
ℏ𝝎
⬢ 𝑛 = 0 ⟶ 𝑛𝑥= 0; 𝑛𝑦 = 0; 𝑛𝑧 = 0 ……no degeneracy
⬢ 𝑛 = 1 ⟶ (𝑛𝑥 = 1; 𝑛𝑦= 0; 𝑛𝑧 = 0 ) (𝑛𝑥 = 0; 𝑛𝑦 = 1; 𝑛𝑧 = 0 ) (𝑛𝑥 = 0; 𝑛𝑦 = 0; 𝑛𝑧 = 1
) …….3 degenerate states
Similarly for n=2 we get six degenerate states
⬢ For 𝑛𝑡ℎ
excited state there will be
𝑛+1 𝑛+2
2
degenerate states.

49. Quantum
number(n)
Energy Combinations
(𝑛𝑥 , 𝑛𝑦, 𝑛𝑧)
Number of
degenerate
states
n = 0 3
2
ℏ𝜔
(0,0,0) 1
n = 1 5
2
ℏ𝜔
(1,0,0) (0,1,0)
(0,0,1)
3
n = 2 7
2
ℏ𝜔
(2,0,0) (0,2,0)
(0,0,2)
(0,1,1) (1,0,1)
(1,1,0)
6
For 3D isotropic harmonic oscillator
 Similar to 2D anisotropic harmonic oscillator, there is no
degeneracy in 3D anisotropic harmonic oscillator.

50. Tunnelling

51. Differences
51
Quantum harmonic
oscillator
Classical harmonic
oscillator
Ground state energy is non
zero.
Ground state energy is zero.
Particle can be found outside
the potential barrier also.
The probability of finding the
particle outside the potential
barrier is zero.
In the ground level energy
state, probability density
distribution is largest in the
middle
In the ground level energy
state, the probability density
distribution is lowest in the
middle.
The particle spends most of
the time in the middle.
The particle spends most of
the time near the turning point.
https://www.st-
andrews.ac.uk/physics/quvis/simulations_html5/sims/QuantumOscillator/oscillator2.html#:~:text=A%20classical%
%20has%20a,beyond%20the%20classical%20turning%20points

52. Applications
⬢ Zero point motion is used to find the characteristics of a material.
⬢ Quantum harmonic oscillator serves as a basis for describing
many real world phenomena. Ex: molecular vibrations
⬢ The motion of atoms in a molecule.
⬢ Vibration of atoms in a solid leads to the production of phonons.
⬢ Many practical potentials can be treated as harmonic potentials.
The internuclear potential well of a molecule of diatomic gas,
such as oxygen and nitrogen can be taken as harmonic
potential. The vibrational energy levels are given by
𝐸𝑛 = 𝑛 +
1
2
ℏ𝜔
52

53. Summary
 Energy is not zero when the quantum number is zero. (Oscillator never at
rest)
 It models the behavior of many physical systems such as molecular
vibrations.
 Wavefunction does not vanish at the potential boundaries (endless boundary).
 The allowed energies of a quantum oscillator are discrete and evenly spaced.
 Squares of wave functions are non negligible in regions outside of potential
boundaries.
 Molecular vibrational energies are quantized in the harmonic limit.
 For high quantum numbers, the motion of a quantum oscillator becomes
similar to the motion of a classical oscillator.
53