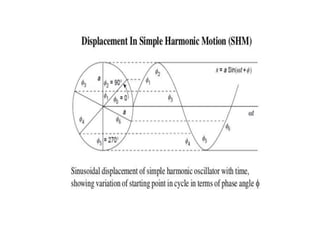
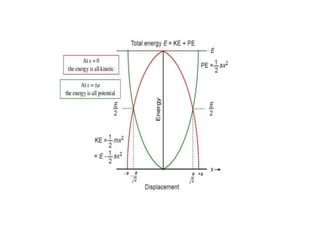
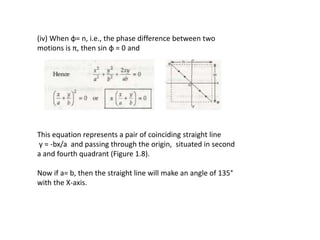
When a particle undergoes two simple harmonic motions perpendicular to each other with the same frequency, the path traced out is called a Lissajous figure. The shape of the figure depends on the amplitudes, frequencies, and phase difference of the motions. Specifically: - With a phase difference of 0, the path is a pair of coinciding straight lines through the origin. - A phase difference of π/2 results in an elliptical path, becoming circular if the amplitudes are equal. - A phase difference of π produces another pair of coinciding straight lines through the origin, at a 135° angle if the amplitudes are equal.

1. B.Sc. I
Paper 01, Unit 02
Simple Harmonic Oscillator
AP Harsha Singh Bais
Assistant Professor
Shri Shankaracharya Mahavidyalaya,Bhilai

15. Lissajou Figure
When a particle is acted upon simultaneously by two SHMs at right angles
or perpendicular to each other, the resultant path traced out by the
particle is closed curve known as Lissajous Figures. named after J.A.
Lissajous, who made an extensive study of these motions.
The nature of the resultant path or the curve traced out depends upon; (i)
the amplitude,
(ii) the period( or frequencies), and
(iii) the phase difference between the component vibrations.
Superposition of Two Mutually Perpendicular Harmonic Motions of the
Same frequencies: Lissajous Figures
Let the displacement of particle executing simple harmonic motion on X-
and Y-axes are x and y respectively, where
x = a sin (wt+θ) ……..1
y= b sin wt …..…2

16. Here a and b are respectively the amplitudes of the
moving particle along X- and Y-axes.
The frequency of both the displacements is same(= w/2π)
and their phase difference is φ.

17. Squaring both the sides we get
………….3
Equation (3) is a general equation of ellipse.
Let us consider a few special cases:
(i) When Q> = 0°, i.e., if the phase difference between the two motions is zero, then sin
φ=0,cos φ=1
……..4
Equation (4) represents a pair of coinciding straight line y = b/a x passing through the origin
in he first and a is zero third quadrant
Now, if a= b i.e., if the amplitudes of the two motions are same, then equation of resultant
curve will be x – y = 0 i.e., the straight time will be at 45° angle from the two axes.

18. (ii) When φ =π/ 4 i.e., the phase difference between the two motions is
n/ 4, then
This is an equation of oblique ellipse Now, if a= b then x
2
+ y
2
– √2 xy = a
2
/2.

19. iii) When φ =π/2, i.e.; the phase difference between the two
motions is π/2′ then
sin φ = 1 and cos φ = 0
Hence …(6)
This is the equation of an ellipse, whose major axis is along X-axis
and minor axis is along Y-axis (Figure 1.7).
Now if a = b,then the equation of resultant curve will be x2 + y2= a2
i.e., the Lissajous figure will now be a circle,
Hence two mutually perpendicular simple harmonic. motions of
same frequency (or same time period) with a phase difference
π/2 are equivalent to a uniform circular motion of radius equal to
the the SHM.

20. (iv) When φ= n, i.e., the phase difference between two
motions is π, then sin φ = 0 and
This equation represents a pair of coinciding straight line
y = -bx/a and passing through the origin, situated in second
a and fourth quadrant (Figure 1.8).
Now if a= b, then the straight line will make an angle of 135°
with the X-axis.