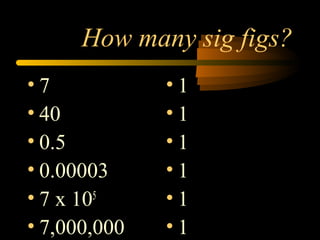This document discusses significant figures and how they are used in science. It defines significant figures as the digits in a measurement that are known with certainty. Measurements are approximate numbers, while amounts of money are exact numbers. When recording measurements, only digits that are dependable based on the precision of the measuring tool are written down. The number of significant figures is determined by counting all digits starting from the first non-zero digit, with some exceptions for trailing zeros. Calculations with measurements require rules for rounding based on the least precise term to determine the number of significant figures in the final answer.

1. Significant Figures
Help with Science and Sig Figs

2. What is a significant figure?
• There are 2 kinds of
numbers:
–Exact: the amount of
money in your account.
Known with certainty.

3. What is a significant figure?
–Approximate: weight,
height—anything
MEASURED. No
measurement is perfect.

4. When to use Significant figures
• When a measurement is
recorded only those
digits that are
dependable are written
down.

5. When to use Significant figures
–If you measured the
width of a paper with
your ruler you might
record 21.7cm.
To a mathematician 21.70,
or 21.700 is the same.

6. But, to a scientist 21.7cm and
21.70cm is NOT the same
• 21.700cm to a scientist
means the measurement
is accurate to within one
thousandth of a cm.

7. But, to a scientist 21.7cm and
21.70cm is NOT the same
• If you used an ordinary
ruler, the smallest
marking is the mm, so
your measurement has
to be recorded as
21.7cm.

8. How do I know how many Sig Figs?
• Rule: All digits are
significant starting with
the first non-zero digit
on the left.

9. How do I know how many Sig Figs?
• Exception to rule: In
whole numbers that end
in zero, the zeros at the
end are not significant.

10. How many sig figs?
• 7
• 40
• 0.5
• 0.00003
• 7 x 105
• 7,000,000
• 1
• 1
• 1
• 1
• 1
• 1

11. How do I know how many Sig Figs?
• 2nd Exception to rule: If
zeros are sandwiched
between non-zero digits,
the zeros become
significant.

12. How do I know how many Sig Figs?
• 3rd Exception to rule: If
zeros are at the end of a
number that has a
decimal, the zeros are
significant.

13. How do I know how many Sig Figs?
• 3rd Exception to rule:
These zeros are showing
how accurate the
measurement or
calculation are.

14. How many sig figs here?
• 1.2
• 2
• 2100
• 2
• 56.76
• 4
• 4.00
• 3
• 0.0792
• 3
• 7,083,000,000
• 4

15. How many sig figs here?
• 3401
• 4
• 2100
• 2
• 2100.0
• 5
• 5.00
• 3
• 0.00412
• 3
• 8,000,050,000
• 6

16. What about calculations with
sig figs?
• Rule: When adding or
subtracting measured
numbers, the answer can have
no more places after the
decimal than the LEAST of
the measured numbers.

17. Add/Subtract examples
• 2.45cm + 1.2cm = 3.65cm,
• Round off to = 3.7cm
• 7.432cm + 2cm = 9.432
round to  9cm

18. Multiplication and Division
• Rule: When multiplying
or dividing, the result
can have no more
significant figures than
the least reliable
measurement.

19. A couple of examples
• 56.78 cm x 2.45cm = 139.111 cm2
• Round to  139cm2
•75.8cm x 9.6cm = ?

20. The End
Have Fun Measuring and
Happy Calculating!