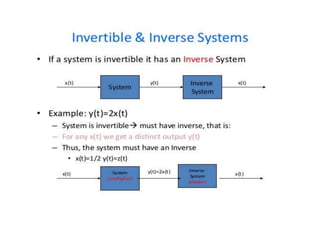
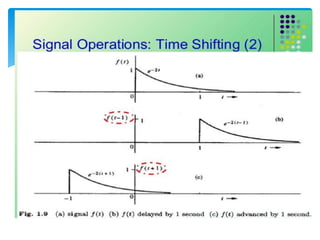
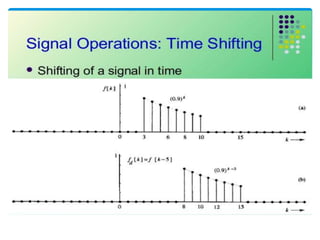
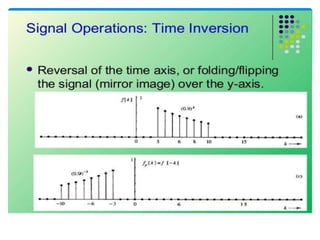
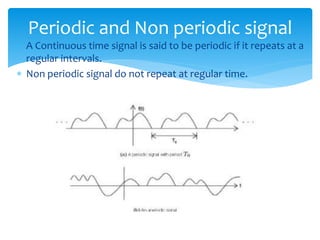
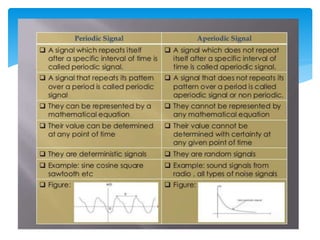
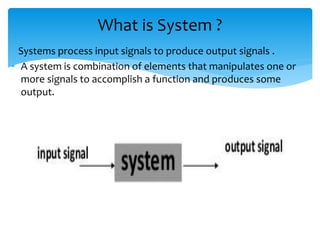
This document discusses digital signal processing and defines key concepts related to signals and systems. It defines a signal as a function of one or more variables that conveys information, and can be one-dimensional or multi-dimensional. Signals are classified as deterministic or random, natural or artificial, continuous or discrete, periodic or non-periodic, causal or non-causal, even or odd, energy-based or power-based. Systems are combinations of elements that process input signals to produce output signals. Systems are classified as static or dynamic, time-invariant or time-variant, linear or non-linear, causal or non-causal, stable or unstable. The document also discusses common operations that can be performed on signals like addition

1. Digital signal processing
Prepared By Md Ibrahim Khalil

2. • Signals are variables that carry information.
• It is described as a function of one or more
independent variables.
• Basically it is a physical quantity . It varies with some
independent or dependent variables.
• Signals can be One-dimensional or multi- dimensional.
Introduction to Signals.
Introduction to signals

3. A function of one or more variables that convey
information on the nature of a physical
phenomenon. Examples: v(t),i(t),x(t),heartbeat,
blood pressure, temperature, vibration.
1.A set of information or data.
2.Function of one or more independent variables.
3. Contains information about the behavior or
nature of some phenomenon
What is signal ?

4.  One-dimensional signals: function depends on a
single variable, e.g., speech signal.
 Multi-dimensional signals: function depends on two
or more variables, e.g., image
 Complex signal : A complex signal that has different
frequency and different amplitude .EX.
 𝑌=5𝑠𝑖𝑛1000𝜔𝑡+ 1/2 𝑐𝑜𝑠5000𝜔𝑡

5. Deterministic and random signals
Natural signal and Artificial Signal
Continuous-time and discrete-time
signals
Periodic and non-periodic signals
Casual and Non-casual signals
Even and odd signals
Energy and power signals
Classification of signals

6.  Behavior of these signals is predictable w.r.t time
 There is no uncertainty with respect to its value at any time.
These signals can be expressed mathematically.
 For example x(t) = sin(3t) is deterministic signal.
Deterministic signals

7.  Behavior of these signals is random i.e. not predictable w.r.t
time.
 There is an uncertainty with respect to its value at any time.
 These signals can’t be expressed mathematically.
 For example : Thermal Noise generated is non deterministic
signal. Random Signals:
Random signals

8. Natural signal are produced by naturally .
Example : Heart beat ,earthquake signal .
Artificial signal does not produce by naturally.
Natural and Artificial signals

9. Continuous Signals: Signals that are defined for all time instants.
Discrete signals: Signals that are defined only for certain time
instants: T, 2T, 3T, ….etc. (T) is the sampling time of the original
continuous signal.
Continuous V/S Discrete Signals

10. Even signals xe(t) and odd signals xo(t) are defined as
xe (t) = xe (−t) and xo (t) = −xo (−t).
Any signal is a sum of unique odd and even signals. Using
x(t) = xe(t)+xo(t) and x(−t) = xe(t) − xo(t), yields
xe(t) =0.5(x(t)+x(−t)) and xo(t) =0.5(x(t) − x(−t)).
Even & Odd Signals

11.  Even:
x(−t) = x(t)
x[−n] = x[n]
 Odd:
x(−t) = −x(t)
x[−n] = −x[n]
 Any signal x(t) can be expressed as
x(t) = xe(t) + xo(t)
x(−t) = xe(t) − xo(t)
where xe(t) = 1/2(x(t) + x(−t))
xo(t) = 1/2(x(t) − x(−t))
Even &Odd Signals

12.  A Continuous time signal is said to be periodic if it repeats at a
regular intervals.
 Non periodic signal do not repeat at regular time.
Periodic and Non periodic signal

14.  A signal is said to be an energy signal if its normalized
energy is nonzero and finite.
 For an energy signal: 0<E<infinite.
 A signal is said to be a power signal if it normalized power is
nonzero and finite.
 For a power signal: 0<p<-infinite.
Energy and Power signal

16. Systems process input signals to produce output signals .
• A system is combination of elements that manipulates one or
more signals to accomplish a function and produces some
output.
What is System ?

17. The Continuous Time & Discrete Time
systems are classified as follows:
 1.Static & Dynamic system
 2.Time invariant & Time variant system
 3.Linear & Non-linear system
 4.Causal & Non-causal system
 5.Stable & Unstable system
 6.Invertible & inverse system
Classification & properties of System

18.  Definition: The continuous time system is said to be
static if its output depends upon the present input
only.
 A static system is memory less system •
 It has no storage devices
 its output signal depends on present values of the
input signal.
Static system

19. Definition :The continuous time system is said to be
static if its output does not depend upon the present
input only.
 A dynamic system possesses memory
 It has the storage devices
 A system is said to possess memory if its output
signal depends on past values and future values of
the input signal.
 Dynamic system consist of integration ,
diffrentiation, delay elements or accumulation term
in their equation.
Dynamic System

22. *A system is said to be time invariant if a time delay
or time advance of the input signal leads to a
identical time shift in the output signal.
*Otherwise the system is called time variant system.
Time Invariant and Time Variant
Systems

23.  A system is said to be linear if it satisfies the principle of
superposition
 For checking the linearity of the given system, firstly we
check the response due to linear combination of inputs
 Then we combine the two outputs linearly in the same
manner as the inputs are combined and again total response
is checked
 If response in step 2 and 3 are the same,the system is linear
othewise it is non linear.
 Important point: Linear system produces zero output if
the input is zero under relaxed condition.
Linear & Non Linear Systems

24.  Definition: The system is said to be causal if its output at
any time depends upon present & past inputs only.
Example: y[n]=x[n]+1/2x[n-1]
 Non-causal system : A system is said to be non-causal if
the present value of the output signal depends only on the
future values of the input signal.
Example: y[n]=x[n+1]+1/2x[n-1]
 Important point: Normally all causal system are physically
realizable. There is no system which can generate the
output for inputs which will be available in future. Such
systems are non-causal, and they are not physically
realizable.
Causal & Non-causal system

25.  A system is said to be bounded-input bounded-
output stable (BIBO stable) if every bounded input
results in a bounded output.
 Otherwise it is called unstable system.
Stable & Unstable Systems

27.  It includes the transformation of independent
variables.
 It is performed in both continuous and discrete
time signals.
 Operations that are performed are
OPERATIONS ON SIGNALS

28.  Let two signals x(t) and y(t) are given,
 Their addition will be, z(t) = x(t) + y(t)
 Their substraction will be, z(t) = x(t) – y(t)
1.ADDITION &SUBSTRACTION

29. If a constant ‘A’ is given with a signal x(t)
z(t) = A.x(t)
 If A>1,it is an amplified signal.
 If A<1,it is an attenuated signal.
2.MULTIPLICATION OF SIGNAL BY A
CONSTANT

30. If two signals x(t) and y(t) are given , than their
multiplication will be
z(t) = x(t).y(t)
3.MULTIPLICATION OF TWO SIGNALS

31.  Let a signal x(t),than the signal x(t-T) represented a
delayed version of x(t),which is delayed by T sec.
4.SHIFTING IN TIME

32. Shifting of a signal in time
 adding or subtracting the amount of the shift to the time
variable in the function.
 x(t) → x(t–t )
 t > 0 (𝑡0 is positive value), signal is shifted to the right
(delay).
 𝑡0 < 0 (𝑡0 is negative value), signal is shifted to the left
(advance).
 x(t–2)? x(t) is delayed by 2 seconds.
 x(t+2)? x(t) is advanced by 2 seconds.
Signal Operations: Time Shifting