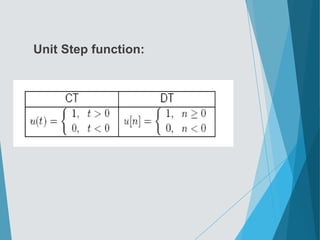
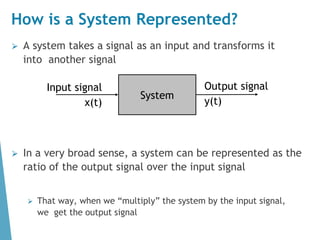
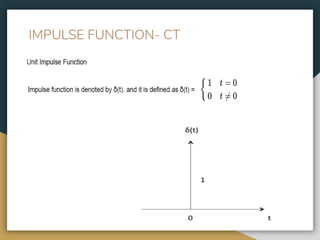
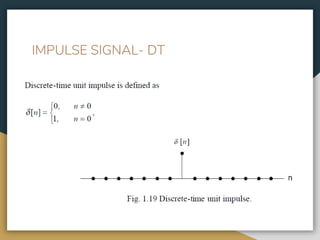
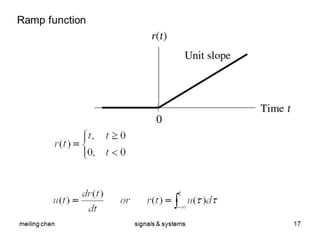
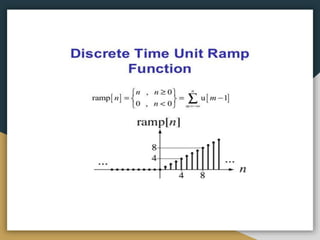
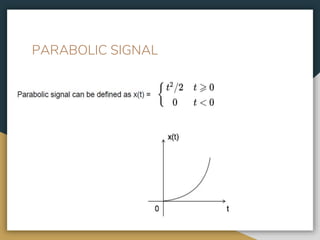
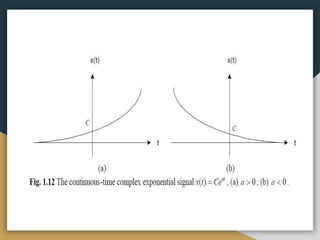
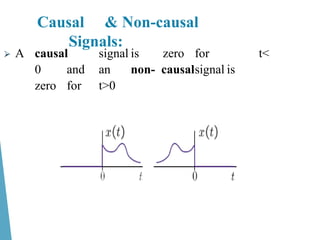
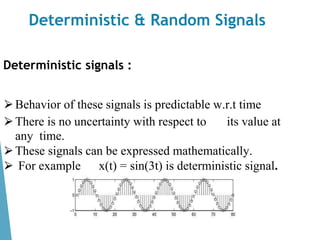
This document contains the course syllabus for the Signals and Systems course at Karpagam Institute of Technology. It covers five units: (1) classification of signals and systems, (2) analysis of continuous time signals, (3) linear time invariant continuous time systems, (4) analysis of discrete time signals, and (5) linear time invariant discrete time systems. The first unit defines common signals like step, ramp, impulse, and sinusoidal signals and classifies signals and systems. It also introduces concepts of continuous and discrete time signals, periodic and aperiodic signals, and deterministic and random signals.

1. EC8352-SIGNALS AND SYSTEMS

2. KARPAGAM INSTITUTE OF TECHNOLOGY,
COIMBATORE - 105
Course Code with Name :OEC753/Signals and Systems
Staff Name / Designation : Mr.S.Pragadeswaran/ AP
Department : ECE
Year / Semester : IV/07
Department of Electronics and Communication Engineering

3. COURSE SYLLABUS
UNIT I CLASSIFICATION OF SIGNALS AND SYSTEMS
Standard signals- Step, Ramp, Pulse, Impulse, Real and complex exponentials and Sinusoids_ Classification of signals –
Continuous time (CT) and Discrete Time (DT) signals, Periodic & Aperiodic signals, Deterministic & Random signals, Energy &
Power signals – Classification of systems- CT systems and DT systems- – Linear & Nonlinear, Time-variant & Time-invariant,
Causal & Non-causal, Stable & Unstable.
UNIT II ANALYSIS OF CONTINUOUS TIME SIGNALS
Fourier series for periodic signals – Fourier Transform – properties- Laplace Transforms and properties
UNIT III LINEAR TIME INVARIANT CONTINUOUS TIME SYSTEMS
Impulse response – convolution integrals- Differential Equation- Fourier and Laplace transforms in Analysis of CT systems –
Systems connected in series / parallel.
UNIT IV ANALYSIS OF DISCRETE TIME SIGNALS
Baseband signal Sampling – Fourier Transform of discrete time signals (DTFT) – Properties of DTFT – Z Transform & Properties
UNIT V LINEAR TIME INVARIANT-DISCRETE TIME SYSTEMS
Impulse response – Difference equations-Convolution sum- Discrete Fourier Transform and Z Transform Analysis of Recursive &
Non-Recursive systems-DT systems connected in series and parallel.

4. UNIT I CLASSIFICATION OF SIGNALS AND
SYSTEMS
Standard signals- Step, Ramp, Pulse, Impulse, Real and complex
exponentials and Sinusoids_ Classification of signals – Continuous time
(CT) and Discrete Time (DT) signals, Periodic & Aperiodic signals,
Deterministic & Random signals, Energy & Power signals -
Classification of systems- CT systems and DT systems- – Linear &
Nonlinear, Time-variant & Time-invariant, Causal & Non-causal,
Stable & Unstable.

5. ⮚ Signals are variables that carry information.
⮚ It is described as a function ofone or more
independent variables.
⮚ Basically it is a physical quantity. Itvaries with
some independent or dependent variables.
⮚ Signals can be One-dimensional or multi-
dimensional
Introduction to Signals

6. ⮚ Signal: A function of one or more variables that
convey information on the nature of a physical
phenomenon.
Examples: v(t),i(t),x(t),heartbeat, blood pressure,
temperature, vibration.
• One-dimensional signals: function depends on a single
variable, e.g., speech signal
• Multi-dimensional signals: function depends on two or
more variables, e.g., image

8. An image is a two dimensional, thats why we also define an
image as a 2 dimensional signal. An image has only height and
width. An image does not have depth. Just have a look at this
image below.

9. ELEMENTARY SIGNALS
❏ Impulse Signal
❏ Step Signal
❏ Ramp Signal
❏ Parabolic Signal
❏ Sinusoidal Signal
❏ Exponential Signal

11. IMPULSE FUNCTION- CT

12. IMPULSE SIGNAL- DT

13. STEP SIGNAL - CT

14. STEP SIGNAL - DT

17. PARABOLIC SIGNAL

18. EXPONENTIAL SIGNAL - CT

20. EXPONENTIAL SIGNAL - DT

21. SINUSOIDAL SIGNAL - CT

22. Classification of signals
⮚ Continuous-time and discrete-time signals
⮚ Periodic and non-periodic signals
⮚ Casual and Non-casual signals
⮚ Deterministic and random signals
⮚ Even and odd signals

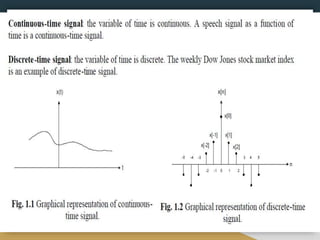
23. Continuous Time (CT) &
Discrete Time (DT) Signals
⮚ CT signals take on real or complex values as a function of an indepe
ndent variable that ranges over the real numbers and are denoted as
x( t ) .
⮚ DT signals take on real or complex values as a function of an
independent variable that ranges over the integers and are denoted as
x[ n] .

24. Periodic & Non-periodic Signals
⮚ Periodic signalshave the property that x( t+T)=
x( t ) for all t .
⮚ The smallest value of T that satisfies
the definition is called the period.
⮚ Shown below are non- periodic s ignal ( left) and a
periodic s ignal ( r ight).

25. ⮚ A causal signal is zero for t<
0 and an non- causalsignal is
zero for t>0
Causal & Non-causal
Signals:

26. Deterministic & Random Signals
Deterministic signals :
⮚Behavior of these signals is predictable w.r.t time
⮚There is no uncertainty with respect to its value at
any time.
⮚These signals can be expressed mathematically.
⮚ For example x(t) = sin(3t) is deterministic signal.

27. ⮚ Behavior of these signals is random i.e.
not predictable
w.r.t time.
⮚ There is an uncertainty with respect to
its value at any time.
⮚ These signals can’t be expressed mathematically.
⮚ For example:Thermal Noise generated is non deterministic
signal.
Random Signals:

28. Even &Odd
Signals
● Even signals xe( t ) and odd signals xo( t ) are
defined as
x e ( t ) = x e ( − t ) a nd x o ( t ) = − x
o ( − t ) .
● Any signal is a sum of unique odd and
even signals.
Us i ng
x( t ) = x e ( t ) + x o ( t )
x ( − t ) = x e ( t ) − x o ( t )

29. Even:
x(−t) = x(t)
x[−n] = x[n]
Odd:
x(−t) = −x(t)
x[−n] = −x[n]
⚫ Any signal x(t) can be expressed as
x(t) = xe(t) +
xo(t) )
x(−t) = xe(t) − xo(t)
where
xe(t) = 1/2(x(t) + x(−t))
xo(t) = 1/2(x(t) − x(−t))
Even &Odd
Signals:

30. Elementary signals
⮚ Step function
⮚ Impulse function
⮚ Ramp function

31. Unit Step function:

32. Unit ramp function:
Unit impulse function:

33. What is a System?
⮚ Systems process input signals to produce output signals.
► Examples:
⮚ A circuit involving a capacitor can be viewed as a system
that transforms the source voltage (signal) to the voltage
(signal) across the capacitor
⮚ A CD player takes the signal on the CD and transforms it into
a signal sent to the loud speaker
⮚ A communication system is generally composed of three
sub- systems, the transmitter, the channel and the receiver.
The channel typically attenuates and adds noise to the
transmitted signal which must be processed by the receiver

34. How is a System Represented?
⮚ A system takes a signal as an input and transforms it
into another signal
⮚ In a very broad sense, a system can be represented as the
ratio of the output signal over the input signal
⮚ That way, when we “multiply” the system by the input signal,
we get the output signal
System
Input signal
x(t)
Output signal
y(t)

35. Types of
Systems
► Causal & Non-causal
► Linear & Non Linear
► Time Variant &Time-invariant
► Stable & Unstable
► Static & Dynamic