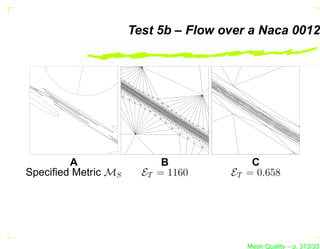
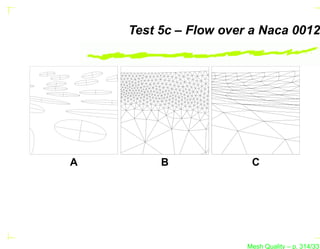
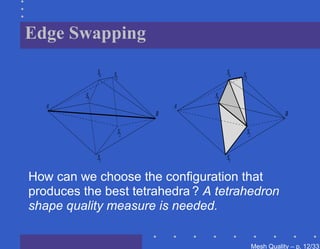
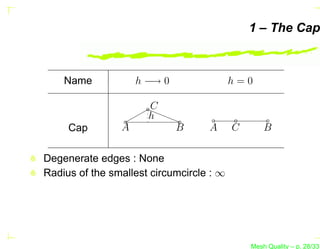
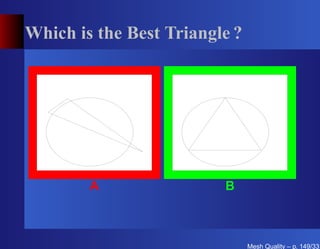
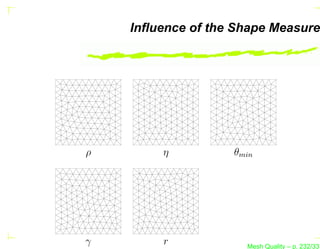
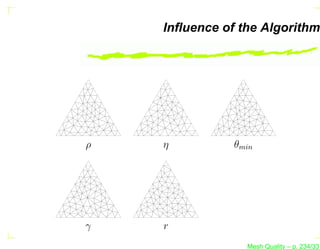
The document discusses mesh quality, emphasizing the importance of measuring the shape quality of simplices in two and three dimensions for mesh generation, adaptation, and optimization. It covers various terms, definitions, and concepts related to simplices, including degeneracies and criteria for identifying degenerate simplices. Additionally, the authors propose benchmarks for optimizing three-dimensional tetrahedral meshes.


























































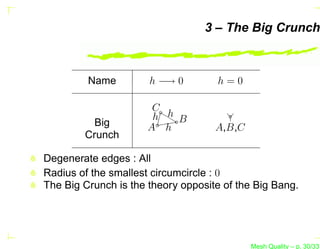

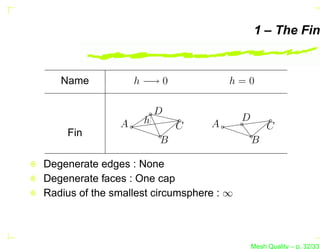
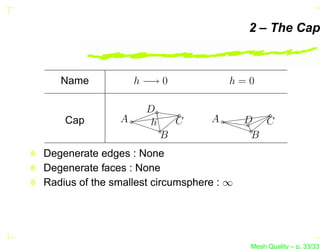

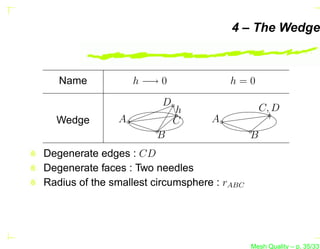















![Simplicial Shape Measure
Definition A : A simplicial shape measure is a
continuous function that evaluates the shape of a simplex.
It must be invariant under translation, rotation, reflection
and uniform scaling of the simplex. A shape measure is
called valid if it is maximal only for the regular simplex and
if it is minimal for all degenerate simplices. Simplicial
shape measures are scaled to the interval [0, 1], and are 1
for the regular simplex and 0 for a degenerate simplex.
Mesh Quality – p. 46/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-84-320.jpg?cb=1317257863)



![The Mean Ratio
Let R(r1 , r2 , r3 [, r4 ]) be an equilateral simplex having the
same [area|volume] than the simplex K(P1 , P2 , P3 [, P4 ]). Let
N be the matrix of transformation from R to K, i.e.
Pi = N ri + b, 1 ≤ i ≤ [3|4], where b is a translation vector.
s y K
K = NR + b
R
r
b
x
Mesh Quality – p. 49/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-89-320.jpg?cb=1317257863)
![The Mean Ratio
Then, the mean ratio η of the simplex K is the ratio of the
geometric mean over the algebraic means of the
eigenvalues λ1 , λ2 [,λ3 ] of the matrix N T N .
√ √
2 λ1 λ2
2
4 3 SK
d
λ +λ = in 2D,
d
λi 1 2
2
1≤i<j≤3 Lij
i=1
η= =
d
1
λi 3 √λ 1 λ 2 λ 3
3
12 3 9VK2
d
i=1 λ +λ +λ = L 2
in 3D.
1 2 3 1≤i<j≤4 ij
Mesh Quality – p. 50/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-90-320.jpg?cb=1317257863)












![There Exists an Infinity of Shape
Measures
If µ and ν are two valid shape measures, if c, d ∈ R+ , then
µc ,
c(µ−1)/µ with c > 1,
αµc + (1 − α)ν d with α ∈ [0, 1],
µc ν d
are also valid simplicial shape measures.
Mesh Quality – p. 64/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-104-320.jpg?cb=1317257863)



















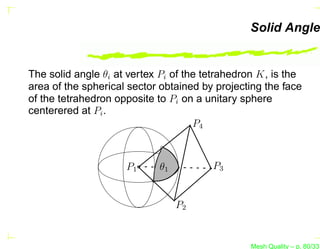












































































![Length in a Variable Metric
In the general sense, the metric tensor M is not
constant but varies continuously for every point
of space. The length of a parameterized curve
γ(t) = {(x(t), y(t), z(t)) , t ∈ [0, 1]} is evaluated in
the metric
1
LM (γ) = (γ ′ (t))T M (γ(t)) γ ′ (t) dt,
0
where γ(t) is a point of the curve and γ ′ (t) is the
tangent vector of the curve at that point. LM (γ) is
always bigger or equal to the geodesic between
the end points of the curve.
Mesh Quality – p. 144/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-203-320.jpg?cb=1317257863)






















































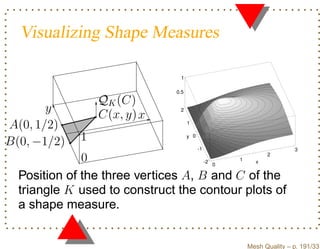
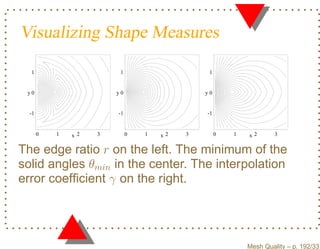
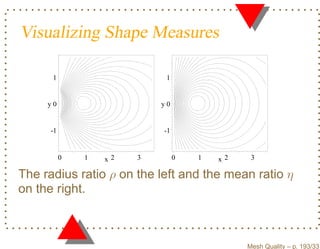

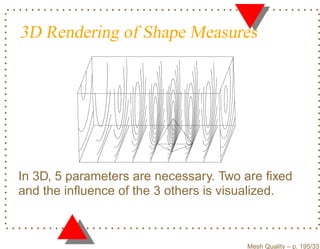
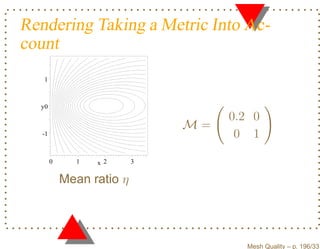
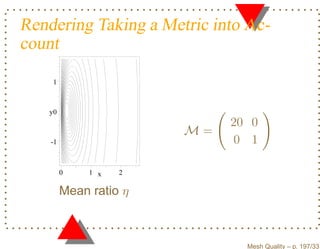
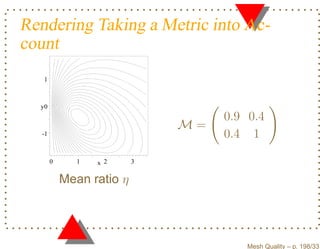
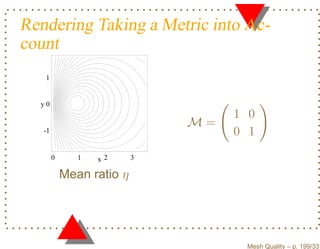







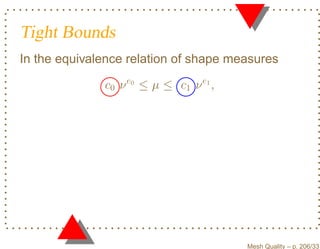
![Equivalence of Shape Measures
Definition B (from L IU and J OE, 1994) : Let µ
and ν be two different simplicial shape measures
having values in the interval [0, 1]. µ is said to be
equivalent to ν if there exists positive
constants c0 , c1 , e0 and e1 such that
c0 ν e0 ≤ µ ≤ c1 ν e1 .
Mesh Quality – p. 204/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-277-320.jpg?cb=1317257863)




















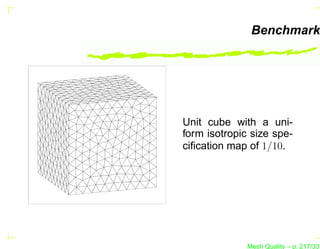
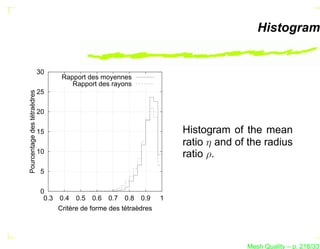
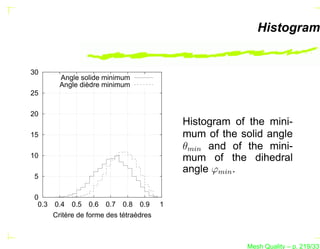

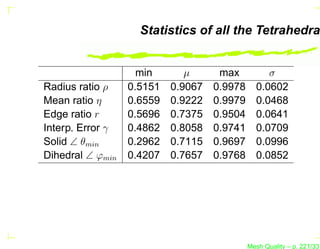











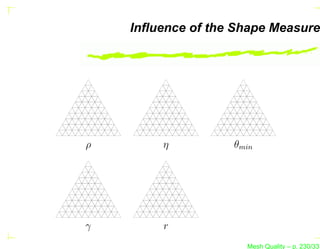





























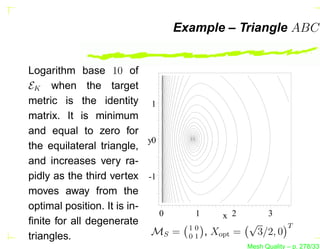
![The Metric MK of a Simplex K
How to compute the metric MK of the transformation that
transforms a simplex K into a unit equilateral element ?
Let P1 , P2 , P3 [, P4 ], the d + 1 vertices of the simplex K
in I d .
R
Let Pi Pj , 1 ≤ i < j ≤ d, the d(d + 1)/2 edges of the simplex.
Mesh Quality – p. 251/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-347-320.jpg?cb=1317257863)




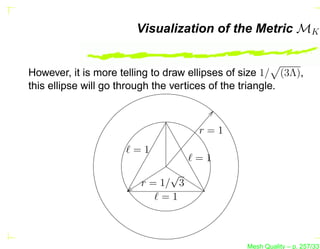
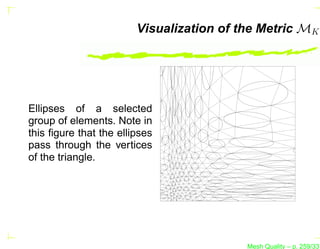
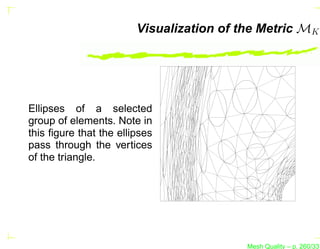
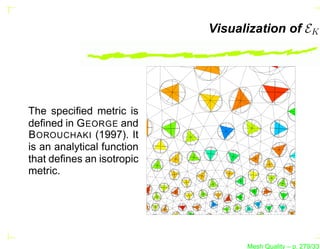
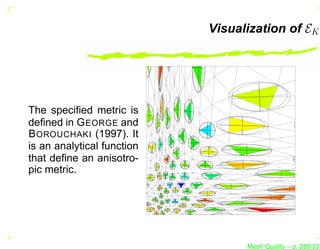
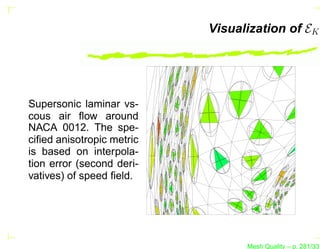
![Visualization of the Metric MK
It is usual to visualize the metric tensor as an ellipse.
Indeed, the metric tensor can be written as
MK = R−1 (θ) Λ R(θ), where the matrix Λ is the diagonal
matrix of the eigenvalues of MK , i.e., Λ = diag(λ1 , λ2 [, λ3 ]).
The eigenvalues λi are the length of the axes of the ellipse
and θ is the rotation matrix of the ellipse about the origin.
Mesh Quality – p. 256/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-352-320.jpg?cb=1317257863)





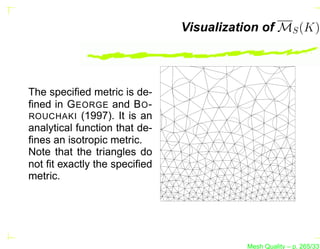

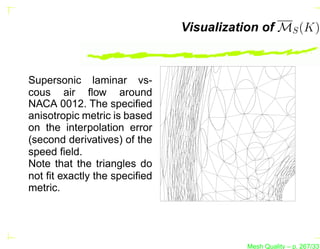












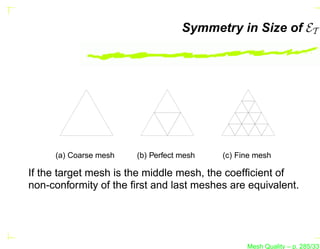











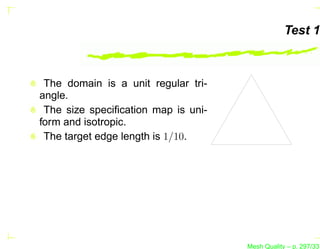
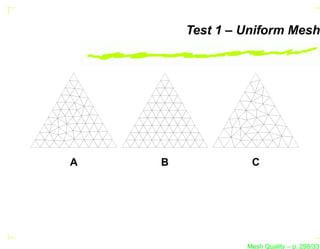
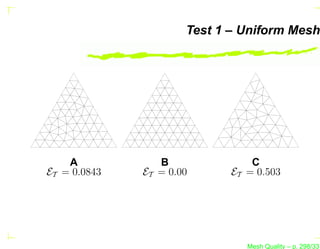
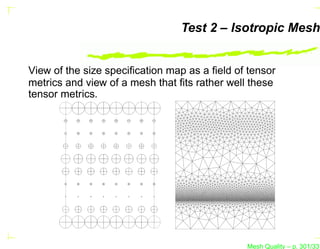
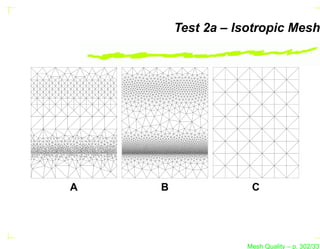
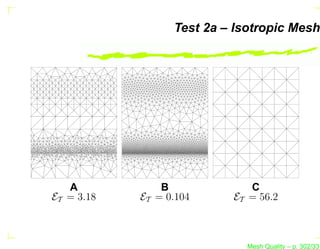
![Test 2 – Isotropic Mesh
This test case is defined in G EORGE and B OROUCHAKI
(1997).
The domain is a [0, 7] × [0, 9] rectangle.
This test case has an isotropic Riemannian metric defined
by :
h−2 (x, y)
1 0
MS = −2 ,...
0 h2 (x, y)
Mesh Quality – p. 299/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-396-320.jpg?cb=1317257863)
![Test 2 – Isotropic Mesh
. . . where h1 (x, y) = h2 (x, y) = h(x, y) is given by :
1 − 19y/40 if y ∈ [0, 2],
(2y−9)/5
20 if y ∈ ]2, 4.5],
h(x, y) =
5(9−2y)/5
if y ∈ ]4.5, 7],
1 4 y−7 4
+
5 5 2
if y ∈ ]7, 9].
Mesh Quality – p. 300/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-397-320.jpg?cb=1317257863)


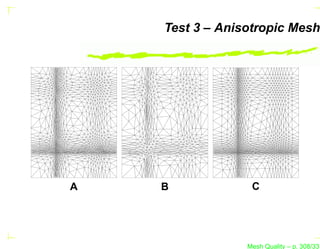
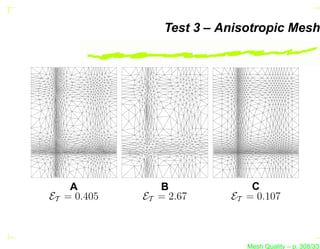
![Test 3 – Anisotropic Mesh
This test case is defined in G EORGE and B OROUCHAKI
(1997).
The domain is a [0, 7] × [0, 9] rectangle.
This test case has an anisotropic Riemannian metric
defined by :
h−2 (x, y)
1 0
MS = ,...
0 h−2 (x, y)
2
Mesh Quality – p. 304/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-403-320.jpg?cb=1317257863)
![Test 3 – Anisotropic Mesh
. . . where h1 (x, y) is given by :
1 − 19x/40
if x ∈ [0, 2],
(2x−7)/3
20 if x ∈ ]2, 3.5],
h1 (x, y) =
5(7−2x)/3
if x ∈ ]3.5, 5],
1 4 x−5 4
5
+5 2 if x ∈ ]5, 7], . . .
Mesh Quality – p. 305/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-404-320.jpg?cb=1317257863)
![Test 3 – Anisotropic Mesh
. . . and h2 (x, y) is given by :
1 − 19y/40
if y ∈ [0, 2],
(2y−9)/5
20 if y ∈ ]2, 4.5],
h2 (x, y) =
5(9−2y)/5
if y ∈ ]4.5, 7],
1 4 y−7 4
5
+5 2 if y ∈ ]7, 9].
Mesh Quality – p. 306/331](https://image.slidesharecdn.com/meshqualityenglish-13172734628063-phpapp02-110929002759-phpapp02/85/Mesh-Quality-405-320.jpg?cb=1317257863)