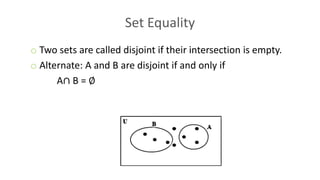
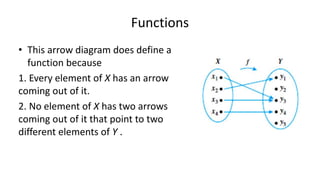
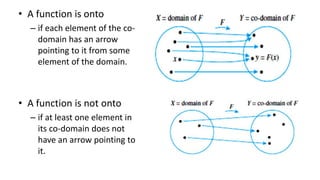
A set is an unordered collection of objects that can be defined by listing elements or describing properties that elements satisfy. Sets are used to build discrete structures like counting, combinations, relations, and graphs. A function from a set X to a set Y is a relation where each element of X is mapped to an element of Y, and no element of X is mapped to more than one element of Y. A function is one-to-one if different elements of the domain map to different elements of the codomain, and onto if every element of the codomain is mapped to by some element of the domain.

2. Sets
o A set is an unordered collection of objects.
o The objects in a set are called the elements or members of
the set S, and we say S contains its elements.
o Sets can be defined by listing their elements
e.g. S = {2, 3, 5, 7, 11, 13, 17, 19},
S = {CS1202, CS542, ERG2020, MAT141}

3. Sets
o Examples of discrete structures built with the help of sets:
o Counting
o Combinations
o Relations
o Graphs

4. Representing Sets by Properties
o It is inconvenient, and sometimes impossible, to define a
set by listing all its elements.
o Alternatively, we can define by a set by describing the
properties that its elements should satisfy.
{x| x has property P}./ {x∈A| P(x)}
set of elements, x, in A such that x satisfies property P.
{x|𝑥 𝑖𝑠 𝑎 𝑟𝑒𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 and -2<x<5}
E = {x| 50 <= x < 63, x is an even integer}

5. Alternative Way of Defining Sets
We can implicitly define a set using a predicate to characterize
its elements.
A= {x ∈ S | P(x)},
the set of all such that
which is read “the set of all x in S such that P of x.”
Define a set using predicate .For example, the set E of even
numbers is
the multiples of 3 between 20 and 30

6. Sets
o Natural numbers:
– ℕ = {0,1,2,3, …}
o Integers
– ℤ = {…, -2,-1,0,1,2, …}
o Positive integers
– Z+ = {1,2, 3.…}
o Rational numbers ℚ
– ℚ = {p/q | p ∈ Z, q ∈ Z, q ≠ 0}

7. Set
o Size of a Set
o The size of a set S, denoted by |S|, is defined as the number of
elements contained in S.
• If S = {2, 3, 5, 7, 11, 13, 17, 19}, then |S|=8.
o NULL SET:
o A set which contains no element is called a null set, or an
empty set or a void set. It is denoted by the Greek letter ∅ (phi)
or { }.
A = {x | x is a person taller than 10 feet} = ∅
( Because there does not exist any human being which is taller then 10 feet )
B = {x | x2 = 4, x is odd} = ∅
(Because we know that there does not exist any odd whose square is 4)

8. Set
o A Subset
– A set A is said to be a subset of B if and only if every element of
A is also an element of B. We use A⊆B to indicate A is a subset
of B.
• ∀x, if x ∈ A then x ∈ B
1. When A  B, then B is called a superset of A.
2. When A is not subset of B, then there exist at least one x  A
such that x B.
3. Every set is a subset of itself
 is regarded as a subset of every set.

9. Set
o Every Set has necessarily two subsets  and the Set itself, these
two subset are known as Improper Subsets and any other subset
is called Proper Subset.
o Given two sets A and B, we say A is a proper subset of B, denoted
by , if every element of A is an element of B, But there
is an element in B that is not contained in A.

10. Set Equality
o Given sets A and B, A equals B, written A = B, if, and only
if, every element of A is in B and every element of B is in
A.
Symbolically:
A = B ⇔ A ⊆ B and B ⊆ A.

11. Set Equality
o Two sets are called disjoint if their intersection is empty.
o Alternate: A and B are disjoint if and only if
A∩ B = ∅

12. Defining Sets
S=T
S ⊆ T
S is a proper subset of T.

13. Set
o UNIVERSAL SET:
The set of all elements under consideration is called the
Universal Set. The Universal Set is usually denoted by U.
o Finite Set
If it contains exactly m distinct elements where m
denotes some non negative integer.
In such case we write |S| = m or n(S) = m
o A set is said to be infinite if it is not finite.

14. Set Operations
Let A and B be subsets of a universal set U.
1. The union of A and B, denoted A ∪ B, is the set of all elements that are in at least
one of A or B.
2. The intersection of A and B, denoted A ∩ B, is the set of all elements that are
common to both A and B.
3. The difference of B minus A (or relative complement of A in B), denoted B − A, is
the set of all elements that are in B and not in A.
4. The complement of A, denoted Ac, is the set of all elements in U that are not in
A.
Symbolically:
A ∪ B = {x ∈ U | x ∈ A or x ∈ B},
A ∩ B = {x ∈ U | x ∈ A and x ∈ B},
B − A = {x ∈ U | x ∈ B and x∉A},
Ac = {x ∈ U | x ∉ A}.

15. Power Set
The power set of a set A is the set of all subsets of A, and is denoted
by 2A. That is,
2A = {S : S⊆A}.
For example, for A = {2, 4, 17, 23}, we have
2A ={∅, {2}, {4}, {17}, {23}, {2, 4}, {2, 17}, {2, 23}, {4, 17}, {4, 23}, {17, 23},{2, 4,
17}, {2, 4, 23}, {2, 17, 23}, {4, 17, 23}, {2, 4, 17, 23}}
The cardinality of this set is 16,

16. Set Identities

17. Functions
• A function f from a set X to a set Y,
– Denoted f : X → Y , is a relation from X, the domain, to Y , the co-
domain,
– that satisfies two properties:
– (1) every element in X is related to some element in Y , and
– (2) no element in X is related to more than one element in Y .

18. Functions
• This arrow diagram does define a
function because
1. Every element of X has an arrow
coming out of it.
2. No element of X has two arrows
coming out of it that point to two
different elements of Y .

19. One-to-One Functions
• Let F be a function from a set X to a set Y . F is one-to-one (or
injective) if, and only if, for all elements x1 and x2 in X,
• if F(x1) = F(x2), then x1 = x2,
• /equivalently, if x1 = x2, then F(x1) = F(x2).
• Symbolically,
– F: X → Y is one-to-one ⇔ ∀x1, x2 ∈ X, if F(x1) = F(x2) then x1 = x2.

20. On-to Functions
• Let F be a function from a set X to a set Y .
• F is onto (or subjective) if, and only if, given any element y in Y
, it is possible to find an element x in X with the property
– that y = F(x).
• Symbolically:
– F: X → Y is onto ⇔ ∀y ∈ Y, ∃x ∈ X such that F(x) = y.

21. • A function is onto
– if each element of the co-
domain has an arrow
pointing to it from some
element of the domain.
• A function is not onto
– if at least one element in
its co-domain does not
have an arrow pointing to
it.