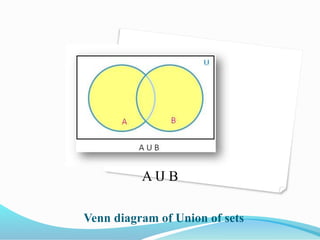
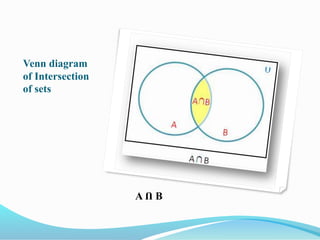
This document defines and provides examples of different types of sets. It discusses the empty set, finite and infinite sets, equal sets, subsets, power sets, and the universal set. Properties of set operations like union and intersection are also covered. Visual representations of sets using Venn diagrams are described.

1. ASHA MERIN SUNNY
Mathematics,
Mangalam College of Education

2.  A set is a well defined collection of
objects.
 Sets are usually denoted by capital
letters A, B, C, X, Y, Z.
 The elements of a set are represented by
small letters a, b, c, x , y , z etc.

3. Different Types Of Sets
 The Empty Set
 Finite and Infinite Sets
 Equal Sets
 Subsets
 Power Set
 Universal Set

4. The Empty Set
 A set which does not contain any element
 Which is also called null set or void set
 It is denoted by ɸ or { }
 Example : C = { x: 1 < x < 2 ,x is a natural number}.Then
C is the empty set ,because there is no natural number
between 1 and 2

5. Finite and Infinite Sets
A set which is empty or consists of a definite number of
elements is called finite set .
Otherwise , the set is called infinite set .
Example:
(ⅰ) Let W be the set of the days of the week.Then W
is finite.
(ⅱ) Let G be the set of points on a line. Then G is
infinite

6. Equal Sets
 Two sets A and B are said to be equal if they have
exactly the same elements otherwise, the set are said
to be unequal.
 A ={ 1, 2 , 3,4 } and B ={ 4, 2, 1, 3 } then, A= B

7. Subsets
 A set ' A' is said to be a subset of 'B' if every element of
A is also an element of B
 It is denoted by A Ϲ B

8. Power Set
 The collection of all subset of a set A is called the power
set of A.
 It is denoted by P(A)
 A ={1, 2} then, P(A) = {ɸ, {1}, {2}, {1,2} }

9. Venn Diagram
 Most of the relationship between sets can be represented
by means of diagrams which are known as Venn diagram.
 Venn diagram are named after the English logician, John
Venn (1834-1883).
 It consists of rectangles and closed curves usually circles.

10. Venn diagram of Union of sets
A Ս B

11. Venn diagram
of Intersection
of sets
A Ո B

12. Properties Of Set Operations
 Union
 A ՍB = BՍA
 (AՍB)ՍC= AՍ(BՍC)
 AՍɸ = A
 AՍA =A
 U ՍA = U
 Intersection
 AՈB=BՈA
 (A Ո B)ՈC =A Ո(BՈ C)
 ɸ Ո A= ɸ
 UՈA=A
 AՈA=A
 AՈ(BՍC)
=(AՈB)Ս(AՈC)