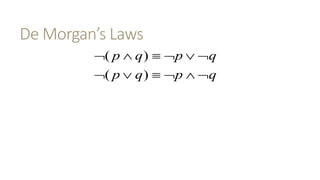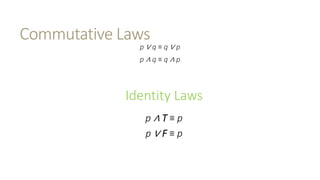
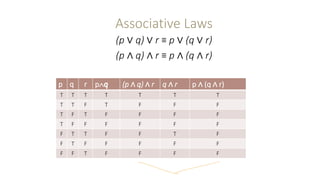
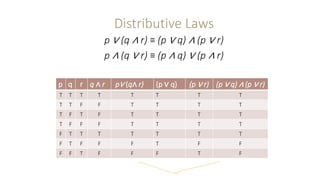
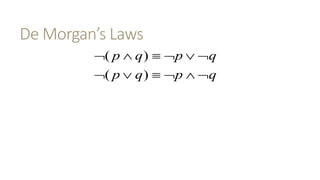
This document outlines several laws of propositional logic, including: - Domination laws which define the relationships between a proposition and true or false. - Idempotent laws which state a proposition is equal to itself repeated. - Commutative laws which allow rearranging order of propositions joined by ∧ or ∨. - Double negation law which states a double negation equals the original proposition. - Associative laws which allow grouping propositions joined by ∧ or ∨. - Distributive laws which define the relationship between ∧ and ∨ when applied to propositions. - De Morgan's laws which define relationships between negated conjunctions and disjunctions. - Negation

3. Domination Laws
p ∨ T ≡ T
p ∧ F ≡ F
Idempotent Laws
p ∨ p ≡ p
p ∧ p ≡ p

4. Commutative Laws
p ∨ q ≡ q ∨ p
p ∧ q ≡ q ∧ p
Identity Laws
p ∧ T ≡ p
p ∨ F ≡ p

5. Double negation Law
￢(￢p) ≡ p

6. Associative Laws
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
p q r pq (p ∧ q) ∧ r q ∧ r p ∧ (q ∧ r)
T T T T T T T
T T F T F F F
T F T F F F F
T F F F F F F
F T T F F T F
F T F F F F F
F F T F F F F

7. Distributive Laws
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
p q r q ∧ r p∨ (q∧ r) (p ∨ q) (p ∨ r) (p ∨ q) ∧ (p ∨ r)
T T T T T T T T
T T F F T T T T
T F T F T T T T
T F F F T T T T
F T T T T T T T
F T F F F T F F
F F T F F F T F

8. De Morgan’s Laws
qpqp
qpqp


)(
)(

9. Negation Law
p ∨￢p ≡ T
p ∧￢p ≡ F
Absorption Laws
p ∨ (p ∧ q) ≡ p
p ∧ (p ∨ q) ≡ p

10. Simplifying Statement Forms
o ∼(∼p ∧ q) ∧ (p ∨ q) ≡ p

11. Exercise