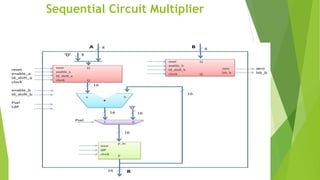
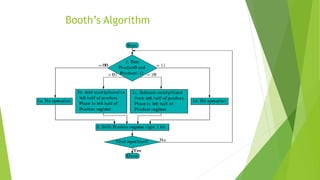
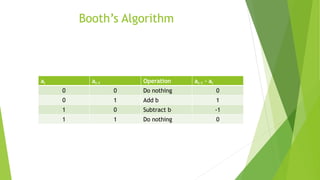
The document discusses different methods for multiplication of binary numbers, including combinational and sequential multipliers. A sequential multiplier uses one parallel adder, registers capable of shifting, and control logic. It multiplies digits through addition and shifting the registers. For signed multiplication, the multiplier and multiplicand may need to be complemented depending on their signs. Booth's algorithm can multiply signed numbers by adding or subtracting the multiplicand instead of just adding, reducing the number of operations.

1. Presentation On:

2. Multiplication
* Combinational Multiplier
* Sequential Multiplier
 Use one parallel adder, a set of registers (capable of shifting), and control logic
 Multiplier “recoding” can be used to reduce the number of adds and subtracts required
 Booth’s Algorithm, Booth Multiplier
 Modified Booth Multiplier
Advantage:
Can use existing registers and ALU
Disadvantage:
Slower than combinational version

3. Observations
 Multiplication of single digits in binary multiplication is just an “AND” operation
 Multiplication of two n-bit numbers can be accomplished with (n-1) additions
 Can use array of AND gates, HA’s, and FA’s

4. Sequential Multiplication Algorithm
• Initialization:
– Load multiplicand in “M” register, multiplier in “Q” register
– Initialize “C” and “A” registers to all zeroes
• Repeat the following steps “n” times, where “n” is the number of bits in the multiplier
– If (LSB of Q register == 1)
-A = A + M (carry-out goes to “C” register)
– Treat the C, A and Q registers as one contiguous register and shift that
register’s contents right by one bit position
• After the completion of “n” steps
– Register “A” contains high-order half of product
– Register “Q” contains low-order half of product

5. Signed Multiplication
• If the multiplier is +ve:
– The unsigned multiplication hardware works fine as long as it is
augmented to provide for sign extension of partial products
• If the multiplier is –ve:
– Form the 2’s-complement of both the multiplier and the multiplicand
and proceed as in the case of a +ve multiplier
– This is possible because complementation of both operands does not
change the value or the sign of the product
• A technique that works equally well for both negative and
positive multipliers – Booth algorithm

6. Sequential Circuit Multiplier

7. Multiplication with Signed Numbers
Case 1: multiplier X and multiplicand Y are positive
Case 2: X is positive and Y is negative
sign-extend the partial products during shifting
use the msb (most significant bit) of the partial product
Case 3: X is negative and Y is positive
add 1 final step of subtracting Y from the partial product
Case 4: both X and Y are negative
apply methods for both Case 2 and Case 3

9. Booth’s Algorithm

10. Booth’s Algorithm
ai ai-1 Operation ai-1 - ai
0 0 Do nothing 0
0 1 Add b 1
1 0 Subtract b -1
1 1 Do nothing 0

11. Booth’s Algorithm
 Booth’s analysis led him to conclude that an ALU that
could add or subtract
could get the same result in more than
one way.
Example: 3 + 4 =7
8 – 1 = 7
At this time shifting was faster than the addition. Hence
reducing the number of additions increased performance.

12. Booth : (7) x (3)
A Q Q-1 M
3 7
---------------------------------------------
0000 0011 0 0111
-------------- -------------------------------
1001 0011 0 0111 A <-(A - M) 1st cycle
1100 1001 1 0111 Shift
----------------------------------------------
1110 0100 1 0111 Shift
----------------------------------------------
0101 0100 1 0111 A <-(A + M) 2nd cycle
0010 1010 0 0111 Shift
----------------------------------------------
0001 0101 0 0111 Shift

13. Booth : (7) x (-3)
A Q Q-1 M
(-3) 7
--------------------------------------
0000 1101 0 0111
--------------------------------------
1001 1101 0 0111 A <- (A - M) 1st cycle
1100 1110 1 0111 Shift
--------------------------------------
0011 1110 1 0111 A <- (A + M) 2nd cycle
0001 1111 0 0111 Shift
--------------------------------------
1010 1111 0 0111 A <- (A - M) 3rd cycle
1101 0111 1 0111 Shift
--------------------------------------
1110 1011 1 0111 Shift

14. Thank You