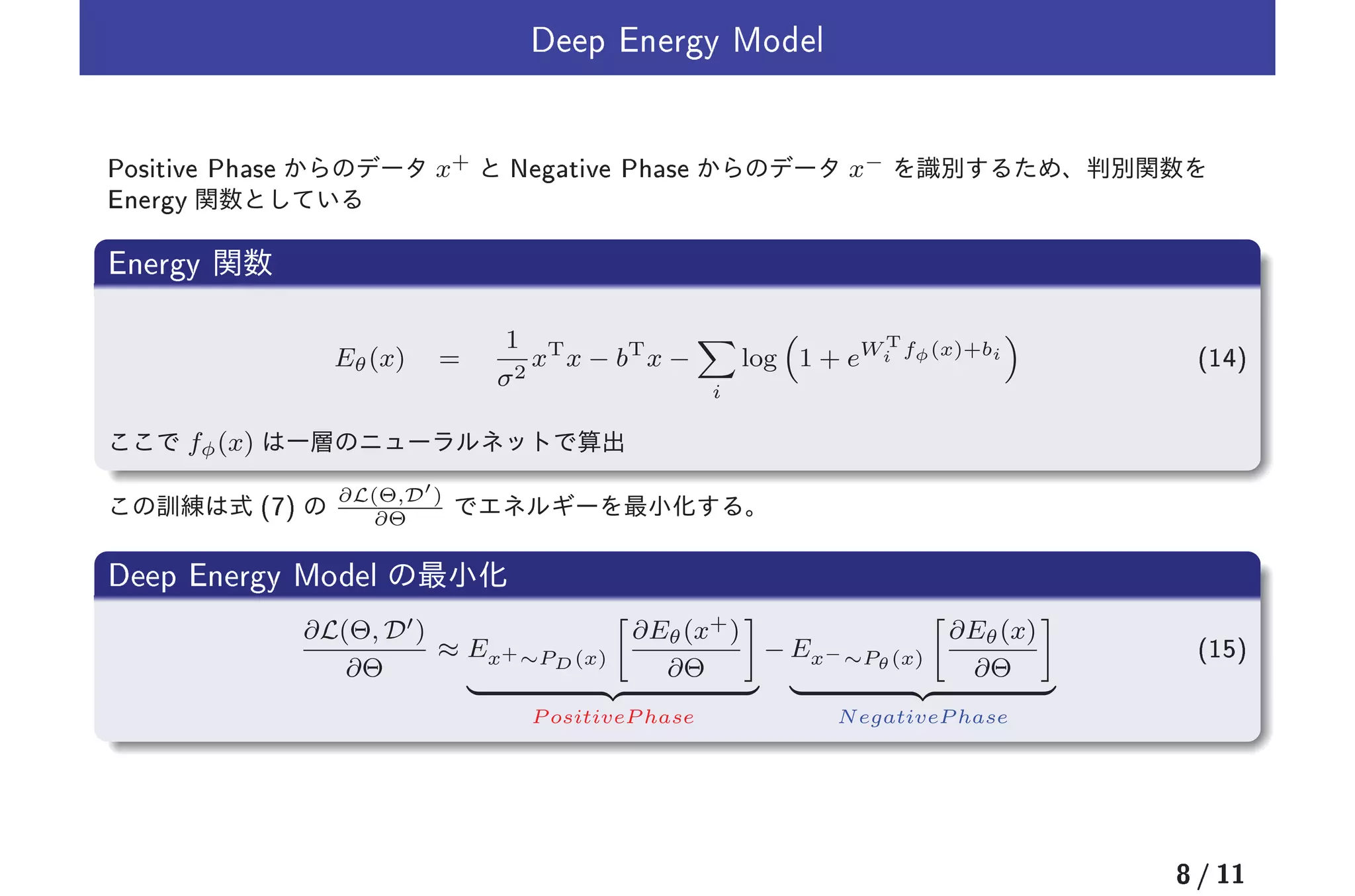
1) The document discusses deep directed generative models that use energy-based probability estimation. It describes using an energy function to define a probability distribution over data and training the model using positive and negative phases. 2) The training process involves using samples from the data distribution as positive examples and samples from the model's distribution as negative examples. The model is trained to minimize the difference in energy between positive and negative samples. 3) Applications discussed include deep energy models, variational autoencoders combined with generative adversarial networks, and adversarial neural machine translation using energy functions.

1. Deep Directed Generative Models with Energy-Based Probability
Estimation
By Yoshua Bengio
mabonki0725
()1
June 16, 2017

2. (1) Alpha
SL 64
RL Q-
(2) AI
(3)
(4)
VAE
GAN
Energy-Base ( )
IRL
Figure:

3. Eθ(x) -NFAHJ
x Eθ(x)
x
Pθ(x) =
1
Z(θ)
exp (−Eθ(x))
Figure: x=0 =1 x= =0 3 / 11

4. EΘ(x)
˜Pθi
(x) =
1
1 + exp −WT
i x + bi
PΘ(x) =
1
ZΘ i
˜Pθi
(x) =
1
ZΘ
eEΘ(x)
EΘ(x) =
i
log 1 + e−(W T
i x+bi)
!
Eθ(x) =
1
σ2
xT
x − bT
x −
i
log 1 + eW T
i x+bi
4 / 11

5. L(Θ, D′
) = −
1
N
N
i=1
log Pθ(x(i)
) (5)
PositivePhase( ) NegativePhase(
∂L(Θ, D′)
∂Θ
= −
1
N
N
i=1
∂ log Pθ(x(i))
∂Θ
= −
1
N
N
i=1
∂ log
exp(Eθ(x(i)
))
Zθ
∂Θ
(6)
= −
1
N
N
i=1
∂ log exp(Eθ(x(i)))
∂Θ
+
∂ log 1
ZΘ
∂Θ
(7)
=
1
N
N
i=1
∂Eθ(x(i))
∂Θ
− Ex∼Pθ(x)
∂Eθ(x)
∂Θ
(8)
≈ Ex+∼PD(x)
∂Eθ(x+)
∂Θ
P ositiveP hase
− Ex−∼Pθ(x)
∂Eθ(x)
∂Θ
NegativeP hase
(9)
5 / 11

6. L(Θ, D′)
x+ x−
Pφ(y = 1|x) = σ(−Eφ(x)) =
1
1 + exp(−Eφ(x))
(10)
P(y = 0) = p(y = 1) = 1
2
Positive Phase Negative Phase
E(x,y)∼P (x,y) −
∂ log Pφ(y|x)
∂φ
= E(x,y)∼P (x,y) −
∂ log Pφ(y = 1|x)yPφ(y = 0|x)(1−y)
∂φ
(11)
= −
1
2
Ex+∼PD(x)
∂ log Pφ(y = 1|x+)
∂φ
+ Ex−∼PΘ(x)
∂ log Pφ(y = 0|x−)
∂φ
(12)
=
1
2
Ex+∼PD(x) Pφ(y = 0|x+
)
∂Eφ(x+)
∂φ
− Ex−∼PΘ(x) Pφ(y = 1|x−
)
∂Eφ(|x−)
∂φ
≈
1
4
Ex+∼PD(x)
∂Eφ(x+)
∂φ
− Ex−∼PΘ(x)
∂Eφ(x−)
∂φ
(13)
6 / 11

7. Deep Generative Model with Enegrgy-Based
2 Positive Phase Negative Phase DeepLearning
Figure:
7 / 11

8. Deep Energy Model
Positive Phase x+ Negative Phase x−
Energy
Energy
Eθ(x) =
1
σ2
xT
x − bT
x −
i
log 1 + eW T
i fφ(x)+bi (14)
fφ(x)
(7) ∂L(Θ,D′
)
∂Θ
Deep Energy Model
∂L(Θ, D′)
∂Θ
≈ Ex+∼PD(x)
∂Eθ(x+)
∂Θ
P ositiveP hase
− Ex−∼Pθ(x)
∂Eθ(x)
∂Θ
NegativeP hase
(15)
8 / 11

9. Deep Generative Model
(Negative Phase )
DKL(Pφ(x)||Pθ(x)) = Ex−∼Pφ(x) − log Pθ(x−
) − H(Pφ(x)) (16)
Negativ Phase
∂
∂φ
Ex−∼Pφ(x) − log Pθ(x−
) =
∂
∂φ
Ez−∼P i(z) − log Pθ(Gφ(z)) (17)
= Ez∼P (z)
∂Eθ(Gφ(z))
∂φ
(18)
≈
1
N
N
i=1
∂Eθ(Gφ(zi))
∂φ
zi ∼ P(z) (19)
Gφ(zi) Deep Network
zi ∼ P(z) (1 ∼ −1)
Negativ Phase
H(Pφ(x)) ≈
αi
H(N(µαi , σi)) =
αi
1
2
log 2 exp(πσ2
αi
) (20)
9 / 11

10. Figure:
Figure:
10 / 11

11. VAE GAN
1 (VAE+GAN
VAE GAN /
Controlable Text Generation by Salakhutdinov
2
Generator
Discrimetor CNN
Adversarial Neural Machine Translation
Energy-Base
GAN
Energy
11 / 11