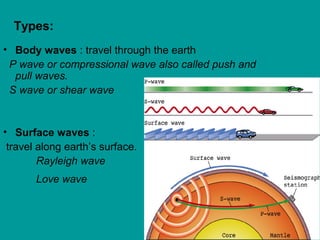
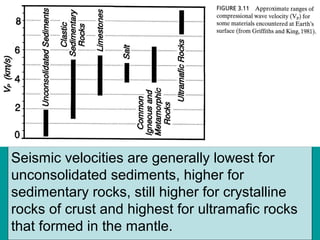
Seismic waves are energy propagated through the earth by earthquakes or artificial sources. There are two types of body waves (P and S waves) that travel through the earth and surface waves (Rayleigh and Love waves) that travel along the earth's surface. Seismic wave velocities depend on the elastic properties and density of the earth materials and are used to determine subsurface layering and structures. Analysis of travel times and slopes of seismic wave arrivals on record sections allows calculation of subsurface velocities and reflection/refraction of waves at interfaces between subsurface layers.

1. SEISMIC WAVES
Department of Geology
Panjab University, Chandigarh.
Submitted By: JAIDEEP KAUR TIWANA
M.Sc. (H.S)- II

2. Seismic waves
• Propagation of energy through the earth
caused by earthquakes or artificial
vibrations.
What is a seismic wave ?
What is the use of its study?
•Seismic refraction data is useful for mapping
depth to bedrock, crustal thickness, and uppermost
mantle velocity.
•Seismic reflection profiles show details of layering
within sedimentary basins and gross structure of
the deeper crust.

3. • Body waves : travel through the earth
P wave or compressional wave also called push and
pull waves.
S wave or shear wave
• Surface waves :
travel along earth’s surface.
Rayleigh wave
Love wave
Types:

4. P wave: Back and forth motion
Particle motions :
S wave: Perpendicular to direction
of wave propagation
Rayleigh wave: retrograde elliptical
motion; at top of ellipse, opposite to
direction of wave propagation.

5. Surface waves
Horizontal motion in direction
perpendicular to direction of wave
propagation.

6. How seismic waves are transmitted ?
The earth materials behave elastically to transmit
seismic waves i.e. the material returns to its original
volume and shape when the stress is removed.
Example : rapid movement of particles results from an
earthquake; at these very high strain rates the asthenosphere
behaves elastically and is thus able to transmit seismic waves.

7. Body wave propagation
• Two elastic constants bulk modulus and
shear modulus will determine how fast
body waves travel through the material.
•Two other constants, are readily measured and used
to calculate k and µ .These are Young’s modulus and
Poisson’s ratio.

8. Bulk modulus: ability of any material to resist being
compressed.
Shear modulus: ability of any material to resist shearing.
Young’s modulus: or stretch modulus – describes the
behavior of a rod that is pulled or compressed.
Poisson’s ratio: ratio of transverse strain to longitudinal strain
for a stretched rod.
Lame’s constant ( λ ) illustrates the relationship between the
four constants discussed above, according to :

9. SEISMIC VELOCITIES
Seismic velocities depend on the elastic constants. ( k , E , µ ,‫)ט‬ and density (ρ)
of material.
 For the same material , shear
waves will always travel slower than
P waves.
The more rigid the material , the
higher the P and S wave velocities.
 Fluids have no shear strength.
(µ) = 0 therefore shear waves
cannot travel through fluids.
 Seismic velocity increase with :
•increasing depth within the earth
•Increase in density
•Decreasing porosity
•Change from liquid to solid.

10. Seismic velocities are generally lowest for
unconsolidated sediments, higher for
sedimentary rocks, still higher for crystalline
rocks of crust and highest for ultramafic rocks
that formed in the mantle.

11. A Wave Front is a surface along which portions of a
propagating wave are in phase.
Particles first move as the wave approaches (wave front at 0° phase).
The maximum amplitude of particle motion occurs along the 90°phase wave
front.
The wave goes from positive to negative amplitude at (180°).
The minimum amplitude of particle motion occurs at (270°).

12. a: Wave fronts represent
the leading edges of
oncoming P,S and
Rayleigh waves (R).
In a homogeneous
medium, the body waves
(P and S) radiate outward
along spherical
wavefronts, while
Rayleigh waves (R) roll
along the surface.
b: Wave fronts for propagating P-wave. Changes in velocity cause
segments of wavefronts to speed up or slow down, distorting the
wave fronts from perfect spheres. Raypaths thus bend (refract) as
velocity changes.

13. a: Initial wave fronts for P,S
and R waves, propagating
across several receivers at
increasing distance from the
source.
b: Travel time graph.
The seismic traces are plotted
according to the distance (X)
from the source to each receiver.
The elapsed time after the
source is fired is the travel time
(T).
T=X/V
Seismic trace is the recording of ground motion by a
receiver plotted as a function of time.
The travel time is a linear,
expressed by the travel time
curve:

14. Slope of the line is elapsed time (∆T) divided by
the distance traveled during the time (∆X):
The travel time can be written:
Slope at distance (X) is the first derivative at that
point on the travel time curve:
so that :
Velocity of wave at
any point on travel
time curve is the
inverse of the slope:

15. When a compressional wave
traveling in one material strikes the
boundary of another material at an
oblique angle, the energy separates
into four phases :reflected P-wave,
reflected S-wave, refracted P-wave,
and refracted S-wave.
Raypaths for direct, reflected and
critically refracted waves, arriving at
receiver a distance (X) from the source.
The interface separating velocity (V1)
from velocity (V2) material is a distance
(h) below the surface.
Behavior of a
refracted ray
when velocity
decreases,
remains same
and increases
across interface.

16. Direct Arrival:
The P wave that goes directly from the source to a receiver is a
body wave traveling very close to the surface.
The velocity of the wave (V1) is the distance from the source to
the receiver (X) divided by the time it takes the wave to travel
directly to the receiver (Td):

17. Velocity of near-surface
material is calculated by
taking inverse of slope of the
direct arrival on the travel time
graph:
The equation for the straight line representing
the direct arrival on a travel-time graph is
therefore:
Td= X/V1

18. Critically Refracted Arrival:
When seismic energy
encounters material of
different velocity, some
of the energy may be
transmitted into second
material; to remain
perpendicular to
wavefronts, raypaths
bend across the
interface.

19. For a wave traveling from material of velocity V1 into
velocity V2 material, raypaths are refracted according to
Snell’s Law:
The Angle of refraction
increases as the angle of
incidence increases.

20. If V2>V1, the angle of refraction
(θ2) can reach 90°. Critical
refraction then occurs, with
energy following the top part of
the higher velocity layer.
 A critically refracted wave,
traveling at the top of the lower
layer with velocity V2, leaks
energy back into the upper layer
at the critical angle(θc).
Angle of incidence for critical
refraction is called Critical angle
(θc).

21. Three segments (T1,T2,T3) comprising the total time path for a critically refracted
ray that returns to the surface. The waves arrive at the surface only at and
beyond the critical distance (Xc). The intercept time (t1) is the projection of
the curve to the T-axis.
Xc= 2h tanθc
h = thickness of
upper layer.

22. This is a
Straight line
equation where
Tr= T1+ T2+ T3

23. At crossover distance
(Xcr) the direct and
critically refracted waves
arrives at the same time;
beyond that the critically
refracted wave arrives
before the direct wave.
CROSSOVER DISTANCE :

24. REFLECTED ARRIVAL:
Reflected waves follow V
shaped paths.
When seismic energy traveling in
one layer encounters a layer with
different acoustic impedance,
some of the energy is reflected
back in to the first layer.
So θ2= θ1
Angle of reflection (θ2) will be
same as angle of incidence (θ1) as
both rays travel at the same
velocity (V1).

25. Total length of reflected path (L) is the sum of raypath
segments for the incident(L1) and reflected segments
(L2):
L= L1+L2

26. Time t0 to go vertically down to the interface and
straight back to the shot location is a constant,
given by:
Travel time equation:
Where t0 is T- axis intercept time.
This is a equation of hyperbola

27. RELATION OF REFLECTED WAVE TO THE DIRECT AND
CRITICALLY REFRACTED ARRIVALS.
LONG DISTANCE FROM THE
SOURCE: As X becomes large,
the T- intercept time (t0) becomes
insignificant:
Tf = Td Reflected wave is
asymptotic to the direct
wave at large distances.

28. At the critical distance
(Xc), the reflected and
critically refracted waves
have the same arrival
time.
The straight line for
the refracted wave is
tangent to the
hyperbola of the
reflection.