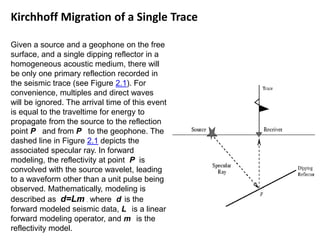
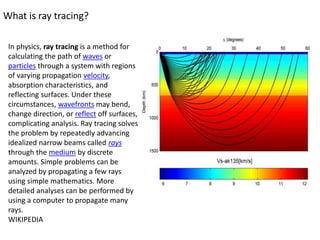
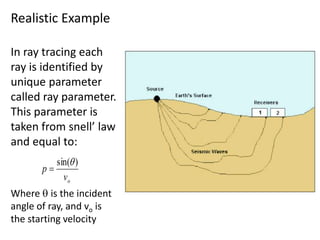
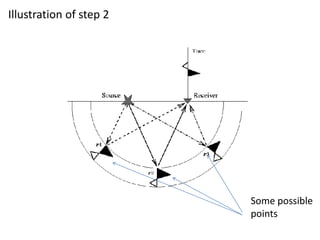
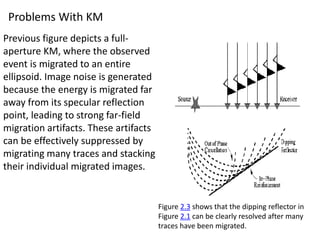
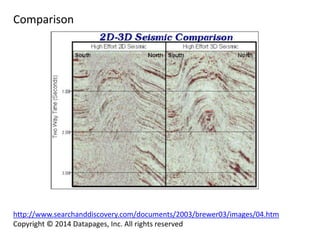
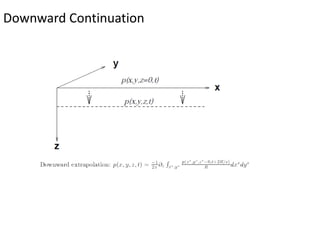
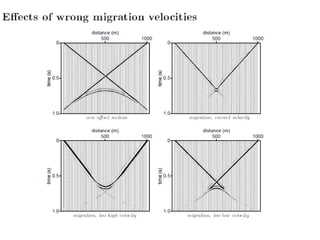
Kirchhoff migration is a widely used seismic data processing method. It works by back projecting observed seismic event energy from traces to possible subsurface reflection points based on traveltime. This smears the event energy to all possible subsurface locations, generating artifacts. Stacking multiple migrated traces helps resolve the true dipping reflector. Ray tracing is used to build the traveltime field. Kirchhoff migration is computationally expensive, taking days to process post-stack or months for pre-stack data. Representing the earth in 3D rather than 2D is preferable but requires knowing the 3D velocity model which is challenging.

1. Seismic Data Processing
Lecture 15
Kirchhoff Migration
Prepared by
Dr. Amin Khalil
School of Physics, USM
2014

2. What is Kirchhoff migration?
Kirchhoff-type migration methods are widely used in
the current oil and gas industry for both depth imaging
and iterative velocity analysis. For migrating a single
event on a single trace, a full-aperture KM smears the
event energy to all possible subsurface points in the
model space. After smearing all samples on all traces,
a KM image is obtained by stacking all individual
contributions. Both the obliquity factor and the
geometric spreading factor are compensated in the KM
algorithm.

3. Kirchhoff Migration of a Single Trace
Given a source and a geophone on the free
surface, and a single dipping reflector in a
homogeneous acoustic medium, there will
be only one primary reflection recorded in
the seismic trace (see Figure 2.1). For
convenience, multiples and direct waves
will be ignored. The arrival time of this event
is equal to the traveltime for energy to
propagate from the source to the reflection
point P and from P to the geophone. The
dashed line in Figure 2.1 depicts the
associated specular ray. In forward
modeling, the reflectivity at point P is
convolved with the source wavelet, leading
to a waveform other than a unit pulse being
observed. Mathematically, modeling is
described as d=Lm , where d is the
forward modeled seismic data, L is a linear
forward modeling operator, and m is the
reflectivity model.

4. The reverse process of seismic forward modeling is
seismic migration which back-projects the observed
energy to its subsurface reflector. Mathematically, the
migrated image is given by m = LT m . To implement
migration, we need to know the medium velocity. By
applying velocity analysis, we can obtain a reasonable
estimate of the velocity distribution. Migration methods
can not be performed without the basic knowledge of the
medium's velocity distribution.
Think how seismic velocity analysis is important to
seismic data processing!!!!
Description

5. KM steps:
1- Apply ray tracing or solve the eikonal equation to build
travel time field for both source and geophone. The travel
time obtained is coarse and can be fine tunned via
interpolation.
2- The next step in KM is to smear the observed energy to
its primary reflection point. This is, however, a blind
operation because we know nothing about where the true
reflection point is. As a result, we have to migrate the event
to all possible reflection points. Such image points are those
whose reflection traveltimes are equal to the observed
traveltime of the event.

6. What is ray tracing?
In physics, ray tracing is a method for
calculating the path of waves or
particles through a system with regions
of varying propagation velocity,
absorption characteristics, and
reflecting surfaces. Under these
circumstances, wavefronts may bend,
change direction, or reflect off surfaces,
complicating analysis. Ray tracing solves
the problem by repeatedly advancing
idealized narrow beams called rays
through the medium by discrete
amounts. Simple problems can be
analyzed by propagating a few rays
using simple mathematics. More
detailed analyses can be performed by
using a computer to propagate many
rays.
WIKIPEDIA

7. Realistic Example
In ray tracing each
ray is identified by
unique parameter
called ray parameter.
This parameter is
taken from snell’ law
and equal to:
ov
p
)sin(

Where  is the incident
angle of ray, and vo is
the starting velocity

8. Illustration of step 2
Some possible
points

9. Problems With KM
Previous figure depicts a full-
aperture KM, where the observed
event is migrated to an entire
ellipsoid. Image noise is generated
because the energy is migrated far
away from its specular reflection
point, leading to strong far-field
migration artifacts. These artifacts
can be effectively suppressed by
migrating many traces and stacking
their individual migrated images.
Figure 2.3 shows that the dipping reflector in
Figure 2.1 can be clearly resolved after many
traces have been migrated.

10. The problem is solved?!!!
Answer: To some extent, since some misleading
information may results in far-field artifacts!!!
This means that at far-field of the KM-ellipsoid we may
obtain false reflector, due to violation of the antiphase
criteria at certain range of the aperture.
Possible solution is to apply anti-alias filter.

11. More Problems
Generally, KM method is
computationally expensive,
meaning it requires large time of
computation at powerful
computers called supercomputers
or PowerStation. For post-stack
applications the method may take
days in computation. For prestack
we may need months.

12. 3D Vs 2D
So far we were dealing with 2D seismic profile.
Again this is an approximation to the medium, in
which we assume that the physical properties
change only with spatial coordinates; namely; the
horizontal X direction and vertical Z direction.
The y direction neglected or in other words the
physical parameters is assumed constant in that
direction. Is this assumption valid for all cases?

13. Why 3D?!!!
Because:
1- The earth change its properties in three
dimensions.
2- In 2D we may get reflections and diffraction
from points outside the plane. Thus all our
migration will fail or become misleading.

14. Comparison
http://www.searchanddiscovery.com/documents/2003/brewer03/images/04.htm
Copyright © 2014 Datapages, Inc. All rights reserved

15. 3D migration

16. Downward Continuation

17. Artifact
Velocity is needed for applying 3D migration.
In the present case we need to know the
velocity change in 3D meaning with x, y and z
direction which is not feasible. In addition
using velocity which change spatially will also
complicate the problem.