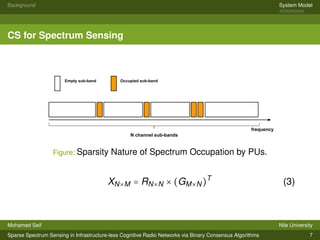
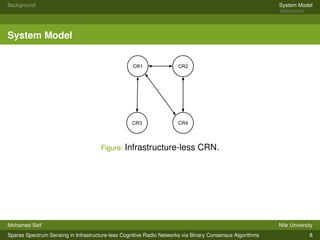
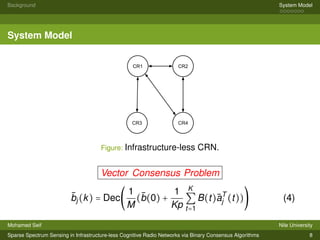
The document presents a system model for sparse spectrum sensing in infrastructure-less cognitive radio networks using binary consensus algorithms. It discusses compressive sensing theory which combines signal acquisition and compression. A vector consensus problem is formulated for an infrastructure-less cognitive radio network where nodes cooperatively sense spectrum occupancy through local interactions. Simulation results show that the infrastructure-less approach achieves detection performance comparable to a centralized architecture and that detection probability increases with the number of measurements and link quality while decreasing with sparsity level.

1. Background System Model
Sparse Spectrum Sensing in
Infrastructure-less Cognitive Radio
Networks via Binary Consensus
Algorithms
Mohamed Seif1
1Wireless Intelligent Networks Center (WINC), Nile University, Egypt
January, 2016
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 1

2. Background System Model
Sampling Theory
Shannon/Nyquist sampling theorem:
No information loss if we
sample at 2x signal bandwidth
DSP revolution: Sample first and ask
questions later (Compression,
Storage, ..., etc)
Increasing pressure on DSP
hardware, algorithms
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 2

3. Background System Model
Compressive Sensing
Compressive sensing (CS) theory combines the signal
acquisition and compression steps into a single step.
The main requirement is that the acquired data is sparse in
some transform domain.
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 3

4. Background System Model
Compressive Sensing
Compressive sensing (CS) theory combines the signal
acquisition and compression steps into a single step.
The main requirement is that the acquired data is sparse in
some transform domain.
x ≈ ∑
K<<N largest terms
αiψi (1)
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 3

5. Background System Model
Compressive Sensing Formulation
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 4

6. Background System Model
Compressive Sensing Formulation
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 5

7. Background System Model
Compressive Sensing Formulation
Signal recovery:
min
x∈RN
x 1 s.t. y − φx 2 ≤ (2)
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 6

8. Background System Model
CS for Spectrum Sensing
frequency
N channel sub-bands
Empty sub-band Occupied sub-band
Figure: Sparsity Nature of Spectrum Occupation by PUs.
XN×M = RN×N × (GM×N)T
(3)
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 7

9. Background System Model
System Model
CR1
CR3
CR2
CR4
Figure: Infrastructure-less CRN.
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 8

10. Background System Model
System Model
CR1
CR3
CR2
CR4
Figure: Infrastructure-less CRN.
Vector Consensus Problem
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 8

11. Background System Model
System Model
CR1
CR3
CR2
CR4
Figure: Infrastructure-less CRN.
Vector Consensus Problem
¯bj(k) = Dec(
1
M
(¯b(0) +
1
Kp
K
∑
t=1
B(t)¯aT
j (t))) (4)
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 8

12. Background System Model
Numerical Results
Simulation Results
Parameter Realization
N 200
T 30
M 12
P 4
dmin 10 m
A 1000 m ×1000 m
K 10
α 2
No. iterations 100
Table: Simulation Parameters.
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 9

13. Background System Model
Numerical Results
Simulation Results
0 5 10 15 20 25
0.4
0.5
0.6
0.7
0.8
0.9
1
SNR (dB)
P
d
Centralized − Majority Rule
Infrastructure−less, K = 10
Infrastructure−less, K = 11
Infrastructure−less, K = 12
Figure: Comperison between two architectures (Fusion based vs
Infrastructure-less).
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 10

14. Background System Model
Numerical Results
Simulation Results
0 5 10 15 20 25
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
SNR (dB)
P
d
p=0.3
p=0.5
p=0.8
Figure: Effect of link quality on probability of detection.
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 11

15. Background System Model
Numerical Results
Simulation Results
0 5 10 15 20 25
0.45
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
SNR (dB)
P
d
T = 30
T = 50
T = 90
Figure: Effect of number of measurements on probability of detection.
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 12

16. Background System Model
Numerical Results
Simulation Results
1 2 3 4 5 6 7 8 9 10
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
P
d
(k)
k
p = 0.2
p = 0.8
Figure: Effect of link quality - (not final)
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 13

17. Background System Model
Numerical Results
Simulation Results
1 2 3 4 5 6 7 8 9 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
k
P
d
(k)
t=150
t=90
Figure: Effect of number of measurements - (not final)
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 14

18. Background System Model
Numerical Results
Thank You!
Mohamed Seif Nile University
Sparse Spectrum Sensing in Infrastructure-less Cognitive Radio Networks via Binary Consensus Algorithms 15