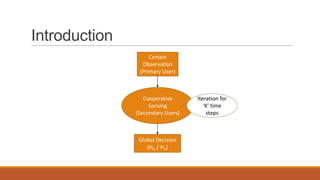
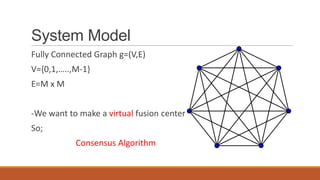
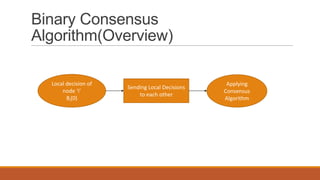
This document describes a binary consensus algorithm for cooperative spectrum sensing in cognitive radio networks. The algorithm uses a fully connected graph model where secondary users cooperatively sense for the presence or absence of a primary user and reach a global decision. Each secondary user makes an initial local binary decision and then iteratively updates its decision by taking the average of its own decision and the decisions received from neighboring nodes. The algorithm is analyzed using a Markov chain representation and the convergence time is related to the second largest eigenvalue of the transition matrix. Simulation results show that the algorithm can accurately detect the presence or absence of a primary user as the number of iterations increases.

1. Binary Consensus
Algorithm
MOHAMED SEIF
COMMUNICATIONS AND ELECTRONICS DEPARTMENT

2. Introduction
Certain
Observation
(Primary User)
Cooperative
Sensing
(Secondary Users)
Global Decision
(H0 / H1)
Iteration for
‘K’ time
steps

3. System Model
Fully Connected Graph g=(V,E)
V={0,1,…..,M-1}
E=M x M
-We want to make a virtual fusion center
So;
Consensus Algorithm

4. Binary Consensus
Algorithm(Overview)
Local decision of
node ‘i’
Bi(0)
Sending Local Decisions
to each other
Applying
Consensus
Algorithm

5. Analysis
First Phase (initial decision) for each agent
Second Phase (Sending Decisions to each other)
-nj,i(k) : a zero-mean Gaussian random variable with variance of σn2.

6. Analysis(Cont’d)
Each agent will update its vote based on the received in information as fellows : R
So, the Decision Rule :

7. Analysis(Cont’d )

8. Markov Chain Representation
-Pi,j will have a binomial distribution as follows :
-ki : represents the probability that any agent votes 1 in the next time step, S(k)=I,
(i.e current state =i)

9. Markov Chain
Representation(Cont’d)
Some Important Properties of P(Transition Matrix):
-By Applying Perron’s theorem, we will have :
1. λo =1, as a simple eigenvalue
2.|λi|< 1 for i ≠ 0
-We are interested in calculating the second largest eigenvalue λ1, which is
important for time convergence analysis

10. Steady State Behavior
A. Case of σn = 0
In this ideal case, the network will reach an accurate consensus in one time step
(all ones / all zeros)
B. Case of σn ≠ 0
The network will reach a steady state asymptotically and is independent of the
initial state

11. Second Largest Eigenvalue
Illustration of its importance :

12. Second Largest Eigenvalue(Cont’d)
Steady
State
Part
Transient
Part

13. Second Largest Eigenvalue(Cont’d)

14. Results

15. Results(Cont’d)

16. Conclusion
Censoring should beat this algorithm in two considerations :
1-The asymptotic behavior in case of σn ≠ 0
2-The time convergence should be smaller than the original case

17. Thank you