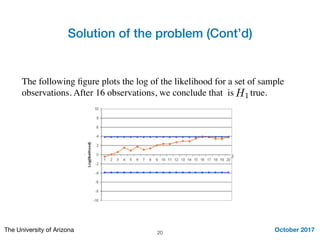
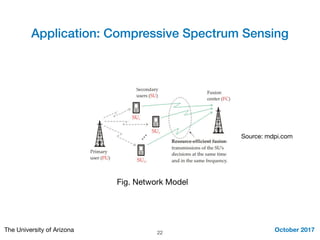
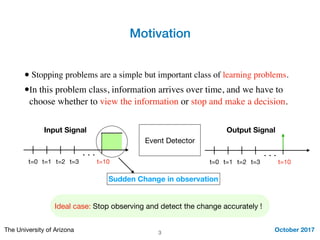
This document summarizes Mohamed Seif's work on stopping problems. It introduces stopping problems, which involve choosing when to stop collecting information and make a decision. It then provides preliminaries on hypothesis testing. The main focus is on the sequential probability ratio test, which sequentially updates probabilities based on likelihood ratios of observations. Thresholds are used to determine when to stop observing and make a decision. The sequential probability ratio test is applied to the problem of compressive spectrum sensing in wireless networks.

1. Stopping Problems
Mohamed Seif, PhD student
ECE Department
October 2017The University of Arizona

2. Outline
October 2017The University of Arizona
• Motivation
• Preliminaries on Hypothesis Testing
• Basic Classic of Stopping Problems
• Sequential Probability Ratio Test
• Proposed Solution
•Application
2

3. Motivation
October 2017The University of Arizona
• Stopping problems are a simple but important class of learning problems.
•In this problem class, information arrives over time, and we have to
choose whether to view the information or stop and make a decision.
3
Event Detector
t=0 t=1 t=2 t=3
. . .
t=10
Input Signal
Sudden Change in observation
t=0 t=1 t=2 t=3
. . .
t=10
Ideal case: Stop observing and detect the change accurately !
Output Signal

4. Preliminaries on Hypothesis Testing
October 2017The University of Arizona
• Consider the following example
depicted in the figure.
• We have two hypotheses:
Fig. Radar System
(
H0, if No air fighter
H1, if Air fighter exist
4

5. Preliminaries on Hypothesis Testing (Cont’d)
October 2017The University of Arizona
• Two sources of error in the
process of detecting air fighter:
1. False alarm
2. Mis detection
Fig. Radar System
=) Prob{ ˆH1|H0}
=) Prob{ ˆH0|H1}
Pe = P(H0)P( ˆH1|H0) + P(H1)P( ˆH0|H1)
• Average probability of error:
5

6. Basic Classes of Stopping Problems
October 2017The University of Arizona
1. Sequential probability ratio test (Talk focus)
2. Secretary problem
6
We have N candidates, interview K out of N
candidates. Then, choose the one who has highest
score.
Decide as quickly as possible when something is
changing.

7. Wn
=
(
¯µ0
+ ✏n
, H0
¯µ1
+ ✏n
, H1
Sequential Probability Ratio Test
October 2017The University of Arizona 7
• For example, we may think we are observing data being generated
by the sequence
• The observed signal at time slot n
• Prior probabilities
Prob(H0) = ⇢0 = ⇢0
0
Prob(H1) = ⇢1 = ⇢0
1

8. Sequential Probability Ratio Test
October 2017The University of Arizona 8
• After observing W1, update the prior using Baye’s rule as follows
⇢1
0 = P(H0|W1
)
=
P(W1
|H0)P(H0)
P(W1)
=
P(W1
|H0)P(H0)
⇢0P(W1|H0) + ⇢0
1P(W1|H1)
Similarly, we can update ⇢1
1 ⇢1
1 = P(H1|W1
)

9. Example
October 2017The University of Arizona
• Consider the observed signal is drawn from Gaussian distribution,
then
9
P(W1
= w|H0) =
1
p
2⇡
exp
✓
1
2
(w ¯µ0
)2
◆
• Let, P0(Wn
) = P(Wn
= wn
|H0)

10. Example
October 2017The University of Arizona 10
⇢n
0 =
⇢0
Qn
k=1 P0(Wk
)
⇢0
Qn
k=1 P0(Wk) + ⇢0
1
Qn
k=1 P1(Wk)
• After n observations,
=
⇢0
n
(W1
, . . . , Wn
⇢0 + ⇢0
1
n(W1, . . . , Wn)
n
(W1
, . . . , Wn
) =
nY
k=1
P0(Wk
)
P1(Wk)
• Where,
)

11. Solution of the problem
October 2017The University of Arizona 11
• Denote the set of all experiments as Sn
= (W1
, . . . , Wn
)
• In the solution / policy , we have two decisions (X⇡
, Y ⇡
)⇡
X⇡
(Sn
) =
(
1, stop and decide
0, continue observing
Y ⇡
(Sn
) =
(
1, Decide H1
0, Decide H0

12. Solution of the problem (Cont’d)
October 2017The University of Arizona 12
• Two sources of error can happen:
1. False alarm: stop and conclude H1
but the true is the null hypothesis H0
2. Mis detection: we did not pick up
any change, i.e., concludeH0 but
H1the alternative hypothesis is true
P⇡
F = E [Y ⇡
(Sn
|H0)]
P⇡
M = E [1 Y ⇡
(Sn
|H1)]
Pe = (1 ⇢0)P⇡
F + ⇢0P⇡
M
• Average probability of error:

13. Solution of the problem (Cont’d)
October 2017The University of Arizona 13
• Let,
N⇡
= min{n|X⇡
(Sn
) = 1}
a random variable that depends on our policy , decision function
and the observations
⇡ X⇡
(W1
, W2
, . . . , Wn
)
• The cost function is defined as follows:
U⇡
(c) = Pe + cE(N⇡
)
where is a scaling coefficient.c

14. Solution of the problem (Cont’d)
October 2017The University of Arizona 14
• The cost function is decomposed into two conditionals risks
r⇡
0 = P⇡
F + cE(N⇡
|H0)
r⇡
1 = P⇡
M + cE(N⇡
|H1)
r⇡
= ⇢0r⇡
0 + (1 ⇢0)r⇡
1
• The total cost is in terms of the conditional risks:
• Now our objective is
R0
(⇢0) = min
⇡
r⇡

15. Solution of the problem (Cont’d)
October 2017The University of Arizona 15
• Special cases:
Then the cost function is
⇢0 = 1 =) N⇡
= 0, P⇡
F = 0, P⇡
M = 0
Similarly, for
R0
(1) = 0
⇢0 = 0 =) R0
(0) = 0
1.
2. If N⇡
= 0, decide Y = 0(i.e., H0) =) R0
(⇢0|Y = 0) = ⇢0
Similarly when N⇡
= 0, decide Y = 1(i.e., H1) =) R0
(⇢0|Y = 1) = 1 ⇢0

16. Solution of the problem (Cont’d)
October 2017The University of Arizona 16
⇢0
0
Risk
0.5
1 ⇢0
0 ⇢0
0
Risk is a concave function
⇢L ⇢U
Stop and decide H1Stop and decide H0
Continue updating priors

17. Solution of the problem (Cont’d)
October 2017The University of Arizona 17
• Now we are interested to obtain ⇢L
, ⇢U
• The updated prior is
⇢n+1
0 =
Ln
(Sn
)
Ln(Sn) + ⇢0/(1 ⇢0)
Ln
(Sn
) =
nY
k=1
P1(Wk
)
P0(Wk)
• The likelihood ratio is defined as

18. Solution of the problem (Cont’d)
October 2017The University of Arizona 18
• Determining if
⇢n+1
0 =
Ln
(Sn
)
Ln(Sn) + ⇢0/(1 ⇢0)
⇢n+1
0 (Sn
)  ⇢L
or ⇢n+1
0 (Sn
) ⇢U
is the same as testing
Ln
(Sn
)  Aor Ln
(Sn
) B
• Why?
Quasi linear function
0
Increasing function for Ln
(Sn
) 0

19. Solution of the problem (Cont’d)
October 2017The University of Arizona 19
• The new bounds A and B are obtained as
A =
⇢n
0 ⇢L
(1 ⇢n
0 )(1 ⇢L)
B =
⇢n
0 ⇢U
(1 ⇢n
0 )(1 ⇢U )
• Now the decision rule is
Ln
(Sn
) =
8
><
>:
B stop and chooseY n
= 1
 A stop and choose Y n
= 0
otherwise continue observing

20. Solution of the problem (Cont’d)
October 2017The University of Arizona 20
The following figure plots the log of the likelihood for a set of sample
observations. After 16 observations, we conclude that is true.H1

21. Solution of the problem (Cont’d)
October 2017The University of Arizona 21
• Since getting A, B exactly is difficult
P⇡
F ⇡
1 A
B A
P⇡
M ⇡
A(B 1)
B A
Wald’s approximation
• Then for an acceptable P⇡
F , P⇡
M
A =
P⇡
M
1 P⇡
F
B =
1 P⇡
M
P⇡
F

22. Application: Compressive Spectrum Sensing
October 2017The University of Arizona 22
Source: mdpi.com
Fig. Network Model