Download to read offline
Uploaded byJuan Victor Chipana Bramon
Pdf integrales
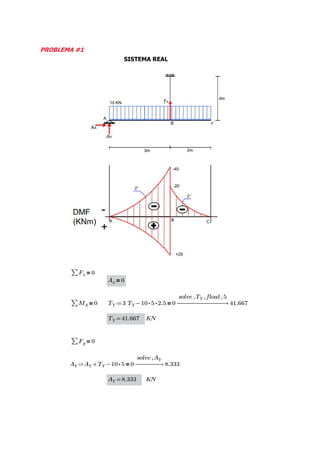
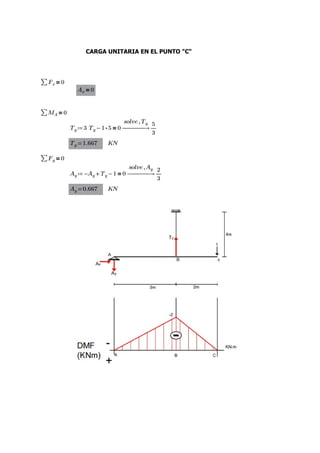
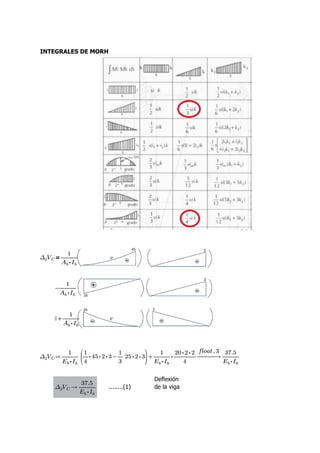
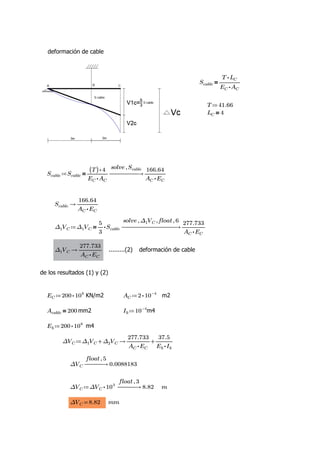
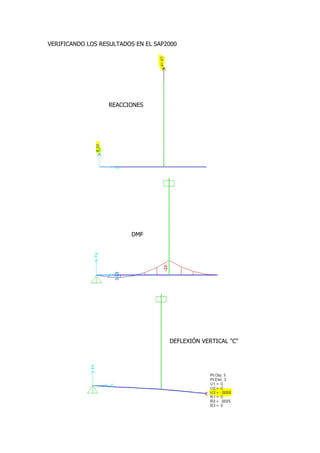
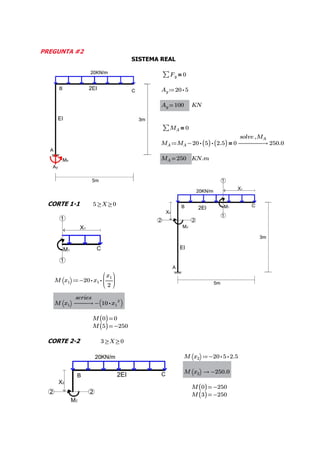
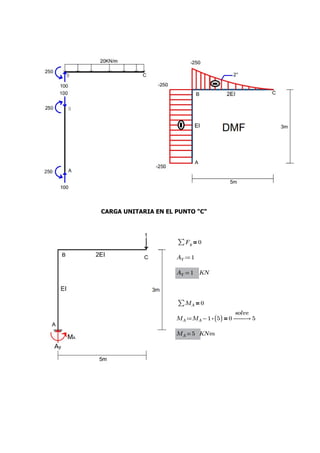
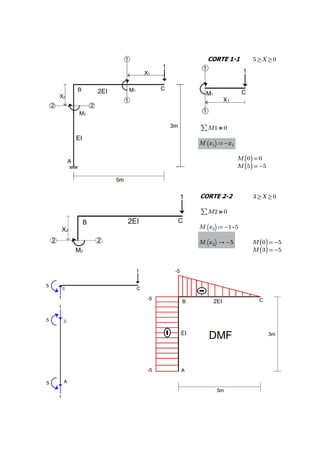
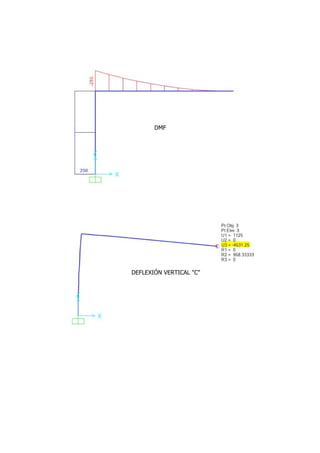
This document contains the solutions to two problems regarding structural analysis from a university course. The first problem involves calculating the deflection of a beam-cable system with given forces and material properties. The second problem calculates the bending moment and deflection of a simply supported beam with a central point load. Diagrams and equations are provided, and the results are verified using SAP2000 software.
More Related Content
Pdf integrales
- 1. UNIVERSIDAD NACIONAL FEDERICO VILLARREAL "SOLUCIÓNINTEGRALES DE MORH" PROFESOR: Ing. Juan Percy Zapata Igreda CURSO: Análisis Estructural 1 SECCIÓN: D ALUMNOS: Ccorpuna Ataucuri Roger Efraín Chipana Bramon Juan Víctor Hilario Bravo Lenin Barroso Pachapuma Jose Rodas Lucar Erika 2021
- 2. PROBLEMA #1 SISTEMA REAL ＝ ∑Fx0 ＝ Ax 0 ＝ ∑MA 0 ≔ TY ―――――― → ＝ - 3 TY ⋅ ⋅ 10 5 2.5 0 , , , solve TY float 5 41.667 = TY 41.667 KN ＝ ∑Fy 0 ≔ AY ――― → ＝ - + AY TY ⋅ 10 5 0 , solve AY 8.333 = AY 8.333 KN
- 3. CARGA UNITARIA ENEL PUNTO "C" ＝ ∑Fx 0 ＝ Ax 0 ＝ ∑MA 0 ≔ Ty ――― → ＝ - 3 Ty ⋅ 1 5 0 , solve Ty ― 5 3 = Ty 1.667 KN ＝ ∑Fy 0 ≔ Ay ――― → ＝ - + -Ay Ty 1 0 , solve Ay ― 2 3 = Ay 0.667 KN
- 4. INTEGRALES DE MORH ＝ Δ2VC―― 1 ⋅ Ab Ib -―― 1 ⋅ Ab Ib +―― 1 ⋅ Ab Ib ≔ Δ2VC ――― → + ―― 1 ⋅ Eb Ib ⎛ ⎜ ⎝ - ⋅ ⋅ ⋅ ― 1 4 45 2 3 ⋅ ⋅ ― 1 3 25 2 3 ⎞ ⎟ ⎠ ⋅ ―― 1 ⋅ Eb Ib ――― ⋅ ⋅ 20 2 2 4 , float 3 ―― 37.5 ⋅ Eb Ib Deflexión → Δ2VC ―― 37.5 ⋅ Eb Ib ........(1) de la viga
- 5. deformación de cable ＝ Scable――― ⋅ T LC ⋅ EC AC ≔ T 41.66 ＝ LC 4 ≔ Scable ―――― → ＝ Scable ――― ⋅ ( (T) ) 4 ⋅ EC AC , solve Scable ――― 166.64 ⋅ AC EC → Scable ――― 166.64 ⋅ AC EC ≔ Δ1VC ――――――― → ＝ Δ1VC ⋅ ― 5 3 Scable , , , solve Δ1VC float 6 ――― 277.733 ⋅ AC EC → Δ1VC ――― 277.733 ⋅ AC EC .........(2) deformación de cable de los resultados (1) y (2) ≔ EC ⋅ 200 106 KN/m2 ≔ AC ⋅ 2 10-4 m2 ＝ Acable 200 mm2 ≔ Ib 10-4 m4 ≔ Eb ⋅ 200 106 m4 ≔ ΔVC → + Δ1VC Δ2VC + ――― 277.733 ⋅ AC EC ―― 37.5 ⋅ Eb Ib ――― → ΔVC , float 5 0.0088183 ≔ ΔVC ――― → ⋅ ΔVC 103 , float 3 8.82 m = ΔVC 8.82 mm VERIFICANDO LOS RESULTADOS EN EL SAP2000
- 6. = ΔVC 8.82 VERIFICANDO LOSRESULTADOS EN EL SAP2000 REACCIONES DMF DEFLEXIÓN VERTICAL "C"
- 7. PREGUNTA #2 SISTEMA REAL ＝ ∑Fy0 ≔ Ay ⋅ 20 5 = Ay 100 KN ＝ ∑MA 0 ≔ MA ――― → ＝ - MA ⋅ ⋅ 20 ( (5) ) ( (2.5) ) 0 , solve MA 250.0 = MA 250 KN.m CORTE 1-1 ≥ ≥ 5 X 0 ≔ M⎛ ⎝x1 ⎞ ⎠ ⋅ ⋅ -20 x1 ⎛ ⎜ ⎝ ― x1 2 ⎞ ⎟ ⎠ ―― → M⎛ ⎝x1 ⎞ ⎠ series -⎛ ⎝ ⋅ 10 x1 2 ⎞ ⎠ = M( (0) ) 0 = M( (5) ) -250 CORTE 2-2 ≥ ≥ 3 X 0 ≔ M⎛ ⎝x2 ⎞ ⎠ ⋅ ⋅ -20 5 2.5 → M⎛ ⎝x2 ⎞ ⎠ -250.0 = M( (0) ) -250 = M( (3) ) -250
- 8. CARGA UNITARIA ENEL PUNTO "C" ＝ ∑Fy 0 ≔ AY 1 = AY 1 KN ＝ ∑MA 0 ≔ MA ―― → ＝ - MA ⋅ 1 ( (5) ) 0 solve 5 = MA 5 KNm
- 9. CORTE 1-1 ≥ ≥ 5X 0 ＝ ∑M1 0 ≔ M⎛ ⎝x1 ⎞ ⎠ -x1 = M( (0) ) 0 = M( (5) ) -5 CORTE 2-2 ≥ ≥ 3 X 0 ＝ ∑M2 0 ≔ M⎛ ⎝x2 ⎞ ⎠ ⋅ -1 5 → M⎛ ⎝x2 ⎞ ⎠ -5 = M( (0) ) -5 = M( (3) ) -5
- 10. INTEGRALES DE MORH ＝ ΔVc+ Δ1 Δ2 *Tramo AB: ＝ LAB 3 = Δ1 ―― 1 EI ≔ Δ1 ―――――→ ⋅ ⋅ ⋅ ―― 1 EI ( (-250) ) ( (-5) ) ( (3) ) , , combine float 6 ――― 3750.0 EI → Δ1 ――― 3750.0 EI
- 11. *Tramo BC: ＝ LBC5 = Δ2 ―― 1 2 EI ≔ Δ2 ―――――― → ⋅ ―― 1 2 EI ⎛ ⎜ ⎝ ⋅ ⋅ ― 1 4 ( (-250) ) ( (-5) ) ( (5) ) ⎞ ⎟ ⎠ , , simplify float 6 ――― 781.25 EI → Δ2 ――― 781.25 EI ≔ ΔVc ―――――― → + Δ1 Δ2 , , simplify float 6 ――― 4531.25 EI ――― → ΔVc simplify ――― 4531.25 EI VERIFICANDO LOS RESULTADOS EN EL SAP2000 REACCIONES
- 12.