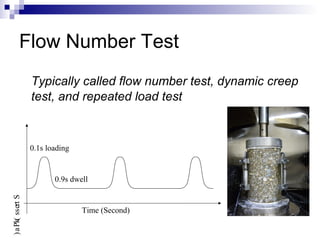
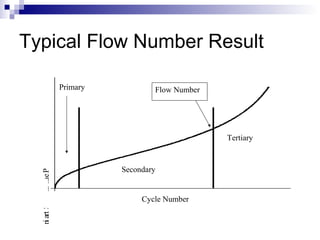
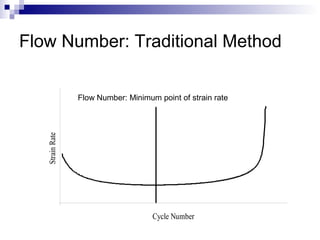
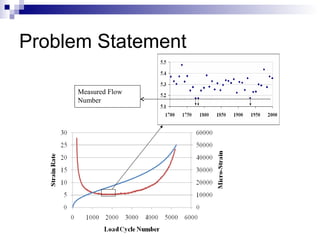
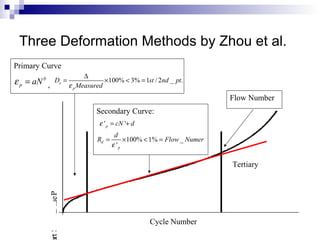
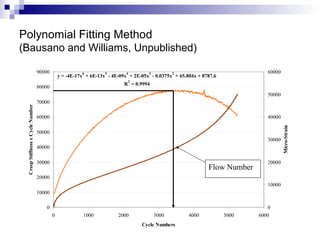
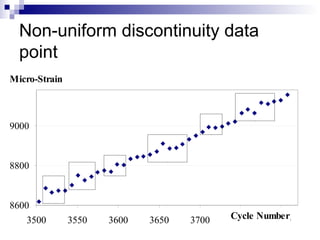
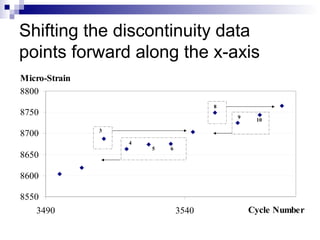
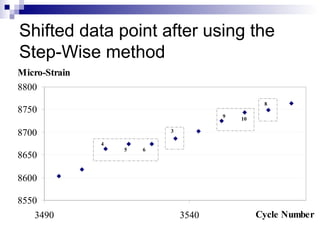
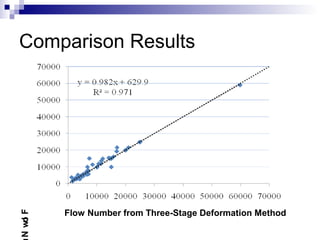
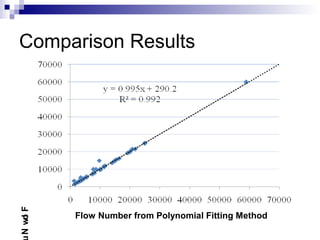
The document presents a step-wise method for determining the tertiary flow in repeated load tests, addressing limitations in existing methods. It evaluates various techniques, including polynomial fitting and three-stage deformation, and demonstrates the effectiveness of the proposed method in providing consistent results. Comparison of flow numbers shows strong correlations with traditional methods, which underlines the validity of the new approach.

1. A Simple Method to Determine
the Tertiary Flow in Repeated
Load Test: Step-Wise Method
By:
Shu Wei Goh
Zhanping You, P.E.

2. Overview
 Introduction of Flow Number
 Problem Statement
 Existing Methods
 Proposed Method
 Comparison Results
 Conclusions

3. Introduction
What is Flow Number?
The point where the asphalt mixture begin
to deform significantly and the individual
aggregates that make up the skeleton of
the matrix start to “flow” –aggregate slide
through each other

4. Flow Number Test
Typically called flow number test, dynamic creep
test, and repeated load test
0.1s loading
Time (Second)
Stress(kPa)
0.9s dwell

5. Typical Flow Number Result
Primary
Secondary
Tertiary
PermanentStrain
Cycle Number
Flow Number

6. Flow Number: Traditional Method
0
0 Cycle Number
StrainRate
Flow Number: Minimum point of strain rate

7. Problem Statement
Measured Flow
Number

8. Existing Methods
 Traditional Method (NCHRP 9-19)
 Polynomial Fitting Method
 Moving Average Periods (MAPs)
 Regression Technique
 Jason Bausano and R. Christopher Williams Method (Unpublished)
 Examined the flow number by plotting creep stiffness times cycles
versus cycle
 Three Stage Deformation Method (By Zhou et al.)
 Using power law model to describe the primary curve and using simple
linear method to describe secondary curve.
 Archilla et al. (2007) Method
 Model the deformation curve by calculating the differential of strain rate
divide by twice the sampling interval, and then smoothed the curve by
running a five-point moving average for each cycle.

9. Three Deformation Methods by Zhou et al.
Tertiary
PermanentStr
Cycle Number
Flow Number
Primary Curve
,
b
p aNε = 100% 3% 1 / 2 _ .e
p
D st nd pt
Measuredε
∆
= × < =
Secondary Curve:
' 'p cN dε = +
100% 1% _
'
d
p
d
R Flow Numer
ε
= × < =

10. Polynomial Fitting Method
(Bausano and Williams, Unpublished)
y = -4E-17x
6
+ 6E-13x
5
- 4E-09x
4
+ 2E-05x
3
- 0.0375x
2
+ 65.804x + 8787.6
R
2
= 0.9994
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
0 1000 2000 3000 4000 5000 6000
Cycle Numbers
CreepStiffnessxCycleNumber
0
10000
20000
30000
40000
50000
60000
Micro-Strain
Flow Number

11. Proposed Methods – Step-Wise
Method
 Assumption:
 Permanent Strain will only increase during flow
number test
 Method using:
 Smoothing the discontinuity data point to provide
step-wise increasing.
 Plot strain rate versus cycle number and defined the
flow number at minimum point of strain rate.
 If the lower strain slope locate at N max, there is no
flow number

12. Non-uniform discontinuity data
point
8600
8800
9000
3500 3550 3600 3650 3700 3750 3800Cycle Number
Micro-Strain

13. Shifting the discontinuity data
points forward along the x-axis
8550
8600
8650
8700
8750
8800
3490 3540 Cycle Number
Micro-Strain
3
4
5 6
8
9
10

14. Shifted data point after using the
Step-Wise method
8550
8600
8650
8700
8750
8800
3490 3540 Cycle Number
Micro-Strain
3
4
5 6
8
9
10

15. Step-Wise Method
 Step 1: Smoothing the measured
permanent deformation by re-allocating
the measured results using the Excel
function call “Sort Ascending.”
 Step 2: Calculate the strain rate using the
modified permanent deformation result.
 Step 3: Determine the flow number by
locating the minimum point of strain rate

16. Comparison Results
Flow Number from Three-Stage Deformation Method
FlowN

17. Comparison Results
Flow Number from Polynomial Fitting Method
FlowN

18. Conclusions
 The proposed approach provides a practical and
consistent method to determine the initiation of tertiary
flow.
 The entire non-uniform discontinuity data point can be
easily smoothed using the excel function called “Sort
Ascending.”
 The R-square value of 0.971 and 0.992 respectively
were found from the comparison and this indicated that
these methods have showed a good correlation with the
proposed Step-Wise method.

19. Question?