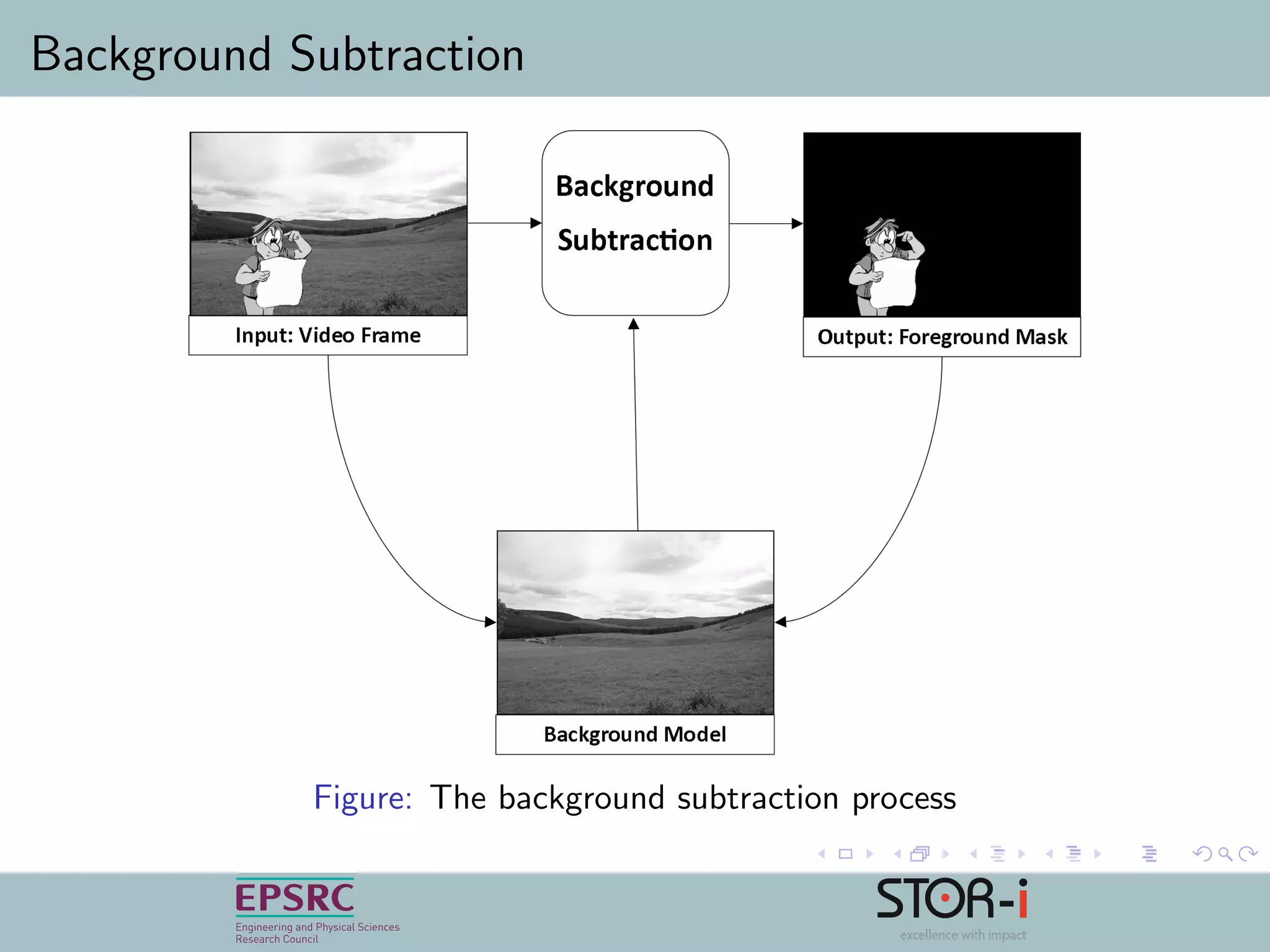
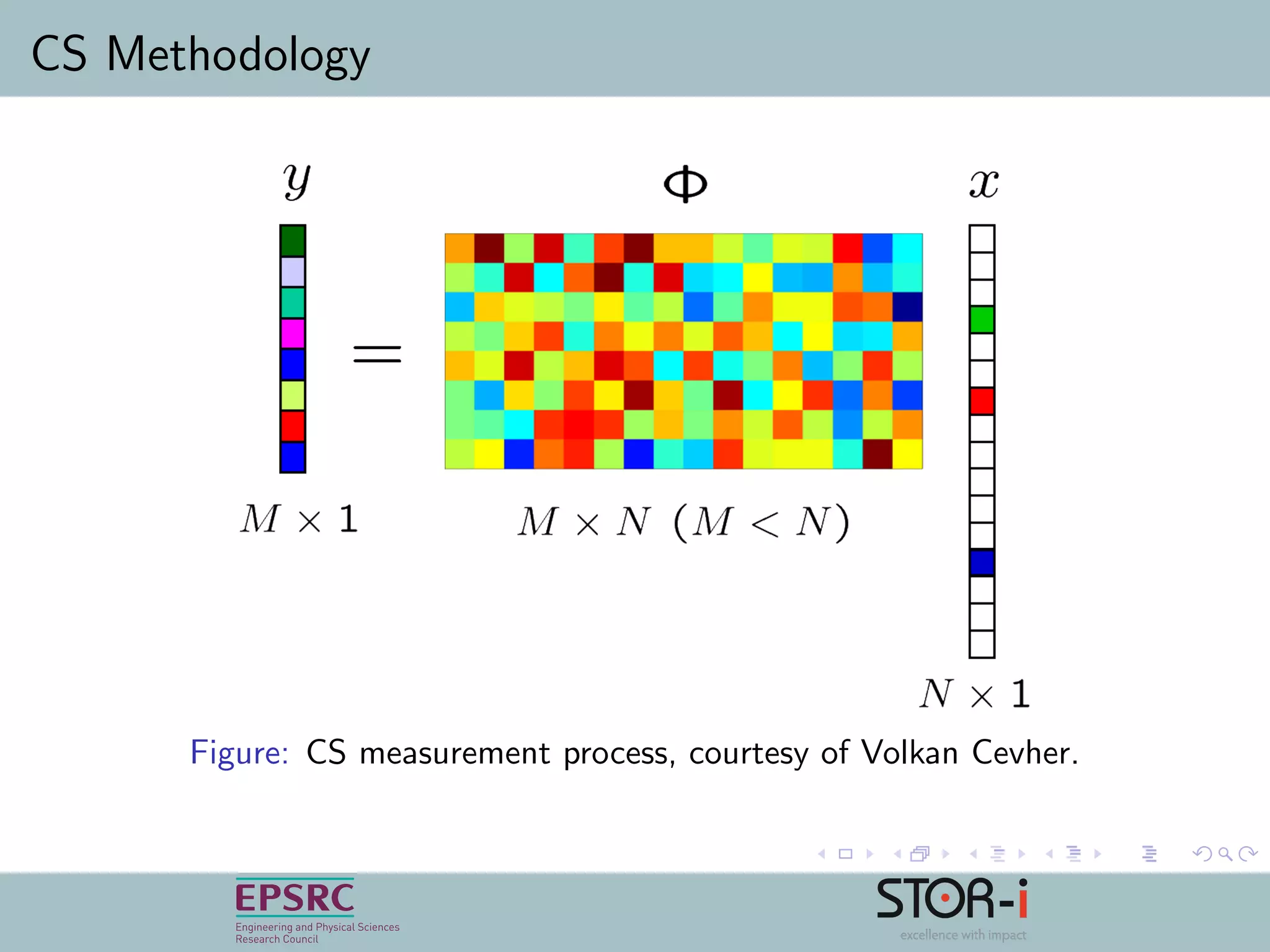
Compressive sensing is a method to reduce the amount of data collected from a signal while still allowing accurate reconstruction later. It works by taking measurements using a matrix that satisfies the restricted isometry property. Sparse signals can be recovered using optimization techniques that minimize the l1 norm. Compressive sensing can be applied to background subtraction in video analysis by compressing the background model and reconstructing the difference between current and background frames to identify foreground objects. Further work includes optimizing the measurement matrix and reconstruction method and adapting to varying sparsity in video frames.

1. Compressive Sensing as a tool for Video Analysis
Rhian Davies
Idris Eckley, Lyudmila Mihaylova, Nicos Pavlidis
August 4, 2013

2. Motivation
“Big Brother is Watching You.”
- George Orwell, 1984

3. What is compressive sensing?
Compressive sensing is a method of reducing the amount of data
collected from a signal without compromising the ability to later
reconstruct the signal accurately.

4. CS Methodology
Figure: CS measurement process, courtesy of Volkan Cevher.

5. Restricted Isometry Property (RIP)
A matrix ΦΦΦ satisfies the Restricted Isometry Property (RIP) of order K if
there exists a δK ∈ (0, 1) such that
(1 − δk)||xxx||2
2 ≤ ||ΦΦΦxxx||2
2 ≤ (1 + δk)||xxx||2
2, (1)
for all xxx ∈ K = xxx : ||xxx||0 ≤ K.

6. Recovery of sparse transforms
y = Φx
∆(y, Φ) = x
Infinitely many solutions!
ˆx = argminy=φx ||x||0
ˆx = argminy=φx ||x||1
Optimisation based on the l1 norm can closely approximate compressible
signals with high probability.

7. Orthogonal Matching Pursuit
We shall define the columns of Φ to be ϕ1, ϕ2, . . . , ϕN each of length M.
Step 1: Find the index for the column of Φ which satisfies
λt = argmax j=1,...,N| < rt−1, ϕj > |
Step 2: Keeps track of the columns used. Λt = Λt−1 ∪ λt,
Φt = [Φt−1, ψλt ]
Step 3: Update the estimate of the signal. xt = argminx ||v − Φtx||2 .
Step 4: Update the measurement residual. rt = y − Φtxt.
Output: Estimated sparse vector ˆx

8. Background Subtraction
Figure: The background subtraction process

9. Foreground sparsity
(a) Original frame (b) Background Model (c) Foreground Mask

10. Background Subtraction with Compressive Sensing.
1. Initialise a compressed background yb
0 .
2. Compressively Sense yt = Φxt.
3. Reconstruct ∆(yt − yb
t )
4. Update Background yb
t+1 = αyi + (1 − α)yb
i

11. Experimentation
Figure: Sanfran test video courtesy of Seth Benton

12. Further Work
Choice of Φ and ∆?
More advanced methods of background subtraction.
Adapting with varying sparsity.
Knowing when to reconstruct.
Exploiting the properties of natural images.

13. Any Questions?