Recommended
PDF
West cork local 9th august
PPTX
Codes and conventions of a horror
PDF
PR Kusuma Trust Donation 13 Apr 2012
PPTX
PPTX
Gustavo grammar book numero dos
PDF
Монтаж сварных ограждений
PDF
PDF
Maintaining a Dynamic View of Semantic Web Services Representing Factory Auto...
PDF
Pengumuman Kelulusan 1415a
PDF
Daftarhadir&nilai belajar&pembelajaran 1415
PDF
Historic Flooding in CO. Big Thompson Canyon - September 2013
DOCX
PPTX
DOCX
Kontrak transaksi perkuliahan1112
PPTX
PhoneBooth:�‘mobilising’ library-owned maps and manuscripts for use in teaching
PDF
PDF
Contoh uji normalitas (ks&lilifors) ks
PPTX
Ulasan jurnal kpt6044 pembelajaran berasaskan elektronik dan web
PPT
miss the forest : bringing together multiple taxonomies
PPT
PDF
Criteria for the design of pressure transducer adapter systems
PPTX
การจัดการเรียนรู้เชิงสร้างสรรค์จากพิพิธภัณฑ์ Sn
PPTX
презентация Microsoft office power point
PPT
PPTX
PPTX
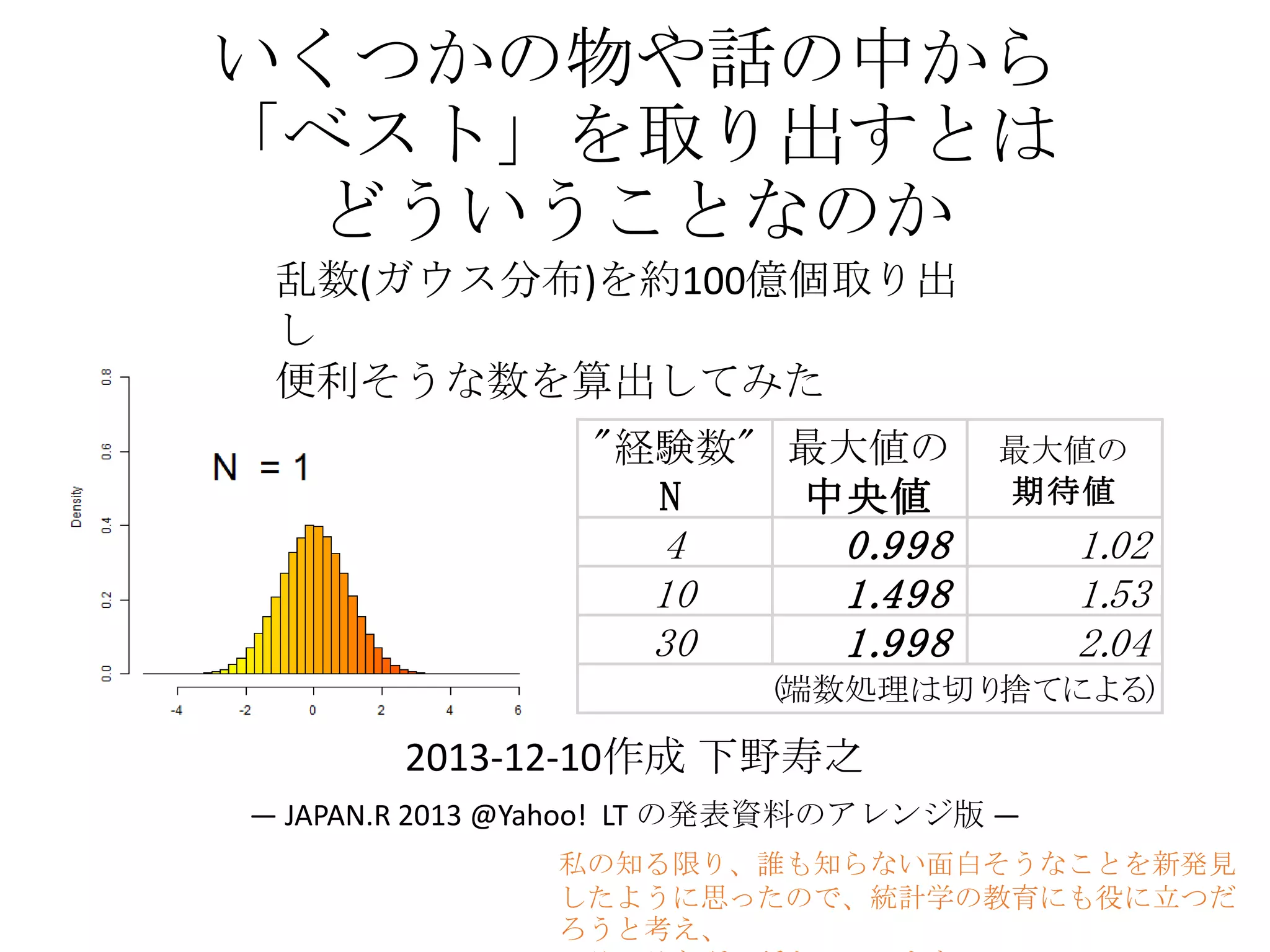
標本抽出で�なぜn=40なのか�についてのある考察
PDF
2016年度秋学期 統計学 第5回 分布をまとめる-平均・分散 (2016. 10. 24)
PDF
2015年度秋学期 統計学 第5回 分布をまとめる ― 記述統計量(平均・分散など) (2015. 10. 28)
PDF
2015年度春学期 統計学 第5回 分布をまとめる ― 記述統計量(平均・分散など) (2015. 5. 14)
PDF
More Related Content
PDF
West cork local 9th august
PPTX
Codes and conventions of a horror
PDF
PR Kusuma Trust Donation 13 Apr 2012
PPTX
PPTX
Gustavo grammar book numero dos
PDF
Монтаж сварных ограждений
PDF
PDF
Maintaining a Dynamic View of Semantic Web Services Representing Factory Auto...
Viewers also liked
PDF
Pengumuman Kelulusan 1415a
PDF
Daftarhadir&nilai belajar&pembelajaran 1415
PDF
Historic Flooding in CO. Big Thompson Canyon - September 2013
DOCX
PPTX
DOCX
Kontrak transaksi perkuliahan1112
PPTX
PhoneBooth:�‘mobilising’ library-owned maps and manuscripts for use in teaching
PDF
PDF
Contoh uji normalitas (ks&lilifors) ks
PPTX
Ulasan jurnal kpt6044 pembelajaran berasaskan elektronik dan web
PPT
miss the forest : bringing together multiple taxonomies
PPT
PDF
Criteria for the design of pressure transducer adapter systems
PPTX
การจัดการเรียนรู้เชิงสร้างสรรค์จากพิพิธภัณฑ์ Sn
PPTX
презентация Microsoft office power point
PPT
Similar to Rr100 b
PPTX
PPTX
標本抽出で�なぜn=40なのか�についてのある考察
PDF
2016年度秋学期 統計学 第5回 分布をまとめる-平均・分散 (2016. 10. 24)
PDF
2015年度秋学期 統計学 第5回 分布をまとめる ― 記述統計量(平均・分散など) (2015. 10. 28)
PDF
2015年度春学期 統計学 第5回 分布をまとめる ― 記述統計量(平均・分散など) (2015. 5. 14)
PDF
PDF
PDF
第6章 2つの平均値を比較する - TokyoR #28
PDF
PDF
PDF
PDF
PDF
PPT
PDF
2022年度秋学期 統計学 第4回 データを「分布」で見る (2022. 10. 18)
PDF
PDF
PDF
MCMCサンプルの使い方 ~見る・決める・探す・発生させる~
PPT
PDF
2022年度秋学期 統計学 第5回 分布をまとめるー平均・分散 (2022. 10. 25)
More from Toshiyuki Shimono
PDF
大量の表形式データを 有効活用するための方法論 – 70個以上のソフトウェア作成からの知見–
PPTX
インターネット等からデータを自動収集するソフトウェアに必要な補助機能とその実装
PPTX
extracting only a necessary file from a zip file
PPTX
A Hacking Toolset for Big Tabular Files -- JAPAN.PM 2021
PDF
新型コロナの感染者数 全国の状況 2021年2月上旬まで
PDF
PDF
PPTX
既存分析ソフトへ
データを投入する前に
簡便な分析するためのソフトの作り方の提案
PPTX
To Make Graphs Such as Scatter Plots Numerically Readable (PacificVis 2018, K...
PPTX
To Make Graphs Such as Scatter Plots Numerically Readable (PacificVis 2018, K...
PDF
Make Accumulated Data in Companies Eloquent by SQL Statement Constructors (PDF)
PPTX
企業等に蓄積されたデータを分析するための処理機能の提案
PPTX
PPTX
PPTX
PPTX
PPTX
PPTX
PPTX
A Hacking Toolset for Big Tabular Files (3)
PPTX
Washingtondc b20161214 (2/3)
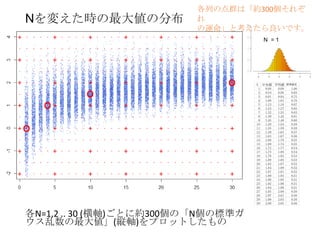
Rr100 b 1. 2. 3. 4. 5. Nを変えた時の最大値の分布
各列の点群は「約300個それぞ
れ
の運命」と考えたら良いです。
N
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
各N=1,2 .. 30 (横軸)ごとに約300個の「N個の標準ガ
ウス乱数の最大値」(縦軸)をプロットしたもの
中央値 平均値 標準偏差
0.
00
0.
00
1.
00
0.
54
0.
56
0.
83
0.
81
0.
84
0.
75
1.
00
1.
03
0.
70
1.
13
1.
16
0.
67
1.
23
1.
27
0.
65
1.
32
1.
35
0.
63
1.
39
1.
42
0.
61
1.
45
1.
49
0.
60
1.
50
1.
54
0.
59
1.
55
1.
59
0.
58
1.
59
1.
63
0.
57
1.
63
1.
67
0.
56
1.
66
1.
70
0.
55
1.
69
1.
74
0.
55
1.
72
1.
77
0.
54
1.
75
1.
80
0.
54
1.
78
1.
82
0.
53
1.
80
1.
85
0.
53
1.
82
1.
87
0.
53
1.
84
1.
89
0.
52
1.
87
1.
91
0.
52
1.
89
1.
93
0.
51
1.
90
1.
95
0.
51
1.
92
1.
96
0.
51
1.
94
1.
98
0.
51
1.
95
2.
00
0.
50
1.
97
2.
01
0.
50
1.
99
2.
03
0.
50
2.
00
2.
05
0.
50
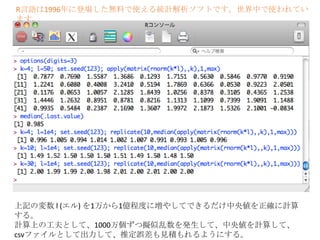
6. 予備知識 : ガウス分布とは
Histogram of runif(1e+06) + runif(1e+06)
60000
20000
Frequency
30000
0
0
10000
Frequency
50000
Histogram of runif(1e+06)
0.0
0.2
0.4
0.6
0.8
1.0
0.0
0.5
runif(1e+06)
1.0
1.5
2.0
runif(1e+06) + runif(1e+06)
120000
80000
Frequency
0
40000
100000
50000
0
Frequency
150000
Histogram of runif(1e+06) + runif(1e+06) + runif(1e+06)
Histogram of runif(1e+06) + runif(1e+06) + runif(1e+06) + runif(1e+06)
0.0
0.5
1.0
1.5
2.0
2.5
3.0
0
runif(1e+06) + runif(1e+06) + runif(1e+06)
1
2
3
4
runif(1e+06) + runif(1e+06) + runif(1e+06) + runif(1e+06)
80000
Histogram of rnorm(1e+06)
[0,1]区間から取り出した一様乱数を2回、3
回、4回と足し合わせたものをヒストグラ
ムにすると、その形は次第に、一定の形に
なる(ベルカーブ,左の図)。 その究極の形
の分布を、「ガウス分布」と呼ぶ。正規
分布とも呼ぶ。
2p s 2
4
ガウス分布は、多くの分布をよく近似す
る。たとえば、身長の分布、体重の分布、
測定誤差を伴う観測の結果の分布などを、
20000
40000
60000
e
平均値μを0、散らばりの尺度である標準
偏差σを1になるように調整したものを特
に、「標準ガウス分布」と呼ぶ。標準正
規分布とも呼ぶ。
0
Frequency
( x- m )2
2s 2
ガウス分布は数ある「分
布」の中で、とてもよく
知られている分布の一つ
です。
-4
-2
0
2
7. 予備知識 : 標準偏差 σ とは
60000
Frequency
40000
20000
0
○ 標準偏差 σ は、データの各値と平均
値の差を2乗したものの平均値に平方
根の操作を加えたものである。
80000
Histogram of rnorm(1e+06, 50, 10)
σは 「振れ幅」 に相当する尺度と考え
ると良い。
0
20
40
60
80
100
rnorm(1e+06, 50, 10)
ガウス分布から乱数 X を取り出した場合、
μ – σ < X < μ + σ となる確率は、68.27%
E
X
E X
2
各データの平均からのズレの2乗を「エネルギー」と考え、その
エネルギー量の期待値から求まる「ズレの相当量」を計算する
ため、平方根(2乗の逆変換)を取った、と考えると良いです。
E[ ・] は期待値です。
(平均値-2σ) は、偏差値30に相当する。
(平均値-σ) は、偏差値40に相当する。
平均値は、偏差値50に相当する。
(平均値+σ) は、偏差値60に相当する。
(平均値+2σ) は、偏差値70に相当する。
μ + σ < X となる確率は 15.87%
μ + 2 σ < X となる確率は、2.275%
μ + 3 σ < X となる確率は、0.135%
μ + 4.5 σ < X となる確率は、100万分の3.4
μ + 6 σ < X となる確率は、10億分の0.99
― 上記の値はR言語のpnorm関数で求まる。
多くの分布は、平均μ と標
準偏差 σ で特徴付けられ
るので、「σ」のこともよ
く理解しておくと、良い
です。
8. 9. 結論
ここに現れる数値の組み合わせが、新発見でし
+1.00σ; 10回: +1.50σ ; 30回: た。
4回:
+2.00σ
"経験数"
N
算出に用いた
乱数の個数 M
最大値の中央値
[下2桁の標準誤差(SD )]
最大値の
期待値
1
―
0
0
4
10
30
41億
41億
51億
0.
998
1.
498
1.
998
147 [22]
802 [29]
224 [40]
各Nについて、M 個の乱数をN個ずつ
に分けて、それぞれの最大値を算出
する。それら(M÷N)個の数の中央値と
平均値が、それぞれ第3列と第4列で
ある。この2個の数は、0.03 程度の差
がある。
1. 93
02
1. 67
53
2. 27
04
やや日常的な解釈:
ガウス分布(μ,σは所与)か
ら、
30個の乱数を取り出す。
「その最大値はぴったり50%
の確率で、μ + 1.998.. σ 」以上
になる。同様に 「~」以下に
なる。
意味が分かれば、記憶しやすく、便利な数。
― 近似するとキリの良い数である。
― どの3個の値も、その近似値マイナス0.002 の操作で、さらに精度が
高まる。
各Nについて、50億個前後の擬似乱数を使いましたが、考えられる計算精度は、小数点
以下第4~5桁目に残っています。上記のような計算では、誤差の2乗に反比例して、乱
数の個数が必要となります。(1桁精度を上げるには、さらに100倍の個数の乱数が必要
10. 分かりやすく結論を言い換えると
(1)
言い換えると
• ベストの物を得たいとき、
• 4回試せば、 (厳密に) 50% の確率で、
平均より +0.998 1.. σ 以上の物が得られる。
• 10回試せば、 (厳密に) 50% の確率で、
平均より +1.498 8.. σ 以上の物が得られる。
• 30回試せば、 (厳密に) 50% の確率で、
平均より + 1.998 2.. σ 以上の物が得られる。
σ への係数をさらに0.5ずつ増加させた場合の、上記の4回、10回、30回に続
く数は、111回、513回、2979回、2万1885回、20万4006回となる。キリの良い
数にはならない。
11. 12. 考察:
• 日常生活や社会生活の上で、反復経験のご利益
がなぜあるか、ひとつの視点を与える、と考え
られる。
• 「4回くらい経験のありそうな人の話は 1σ 話を差し引いて聞いた方が良い」
• 「10回の経験を知っている人の話は、+1.5σ 盛られた話だから、1.5σ 差し引い
て話を聞いた方が良い。」
• 「30回経験したら、そのうち1回くらいは、-2σ前後に相当する経験をする こ
とになる)
• 「便利」な訳 : 記憶しやすい。知ってしまう
と、1週間に1回程度は、日常生活などで出会う
(と思われる)ため。
― 半分冗談で、半分本気です!!
• 標準偏差 σ を推定する問題、そもそも何を尺度にするかという問題につい
ては説明していないが、妥当で適切な理屈はおそらく存在する。そして、
未解決予想を生み出す可能性を秘めている。
中心となる結果は数値的なものであり、統計の用語で定式化して表現された
ものです。そのような表現は具体的に言うと、多くのたとえ話に使えます。
どういう話に使うかについては、別のセンスが必要ですが、いろいろな面白
13. 14. 15. 参考1 : 本資料に用いた元の数表
"経験数"
N
最大値の中央値
[下2桁の標準誤差(SD )]
最大値の
期待値
1
―
0
0
4
10
30
110
111
510
511
512
513
514
515
•
算出に用いた
乱数の個数 M
41億
41億
51億
44億
44.
4億
122.
4億
174.
5億
102.
4億
513億
102.
8億
103億
0.
998 1 4 7
1.
498 8 0 2
1.
998 2 2 4
2.
495 892
2.
499 135
2.
998 102
2.
998 797
2.
999 237
2.
999 884
3.
000 461
3.
001 152
[2 7 ]
[3 5 ]
[4 6 ]
[79]
[84]
[86]
[63]
[96]
[43]
[97]
[99]
1.
02
1.
53
2.
04
2.
54
2.
54
3.
04
3.
04
3.
04
3.
04
3.
04
3.
04
93
67
27
15
47
27
27
27
44
50
56
“最大値の中央値” を 0.5刻みで変化させたときのNがどうなるかを考えようとして、たまたま発見した。
•
意味が解釈可能であって、たまたま、Nが2桁以下のときは全て、Nが記憶のしやすい数であった(4,10,30)。
•
そのときの中央値も小数点以下第3位で切り捨てると、 0.5の整数倍から 0.002 少ない数であった(0.998, 1.498, 1.998)。
•
•
ちょうど0.5の整数倍にはならないので、それに最も近い数を追求していたら、上記のような数表となった。
•
N=111, 511の場合は、小数点以下第3位で切り捨てると、 0.5の整数倍から 0.001 少ない数であった。
上記の表の誤差の可能性について
•
メモリの制約があったため、上記の数は、各Nについて、M個の乱数を、約1000万個ずつに分けて、さらにN個ずつに分けて最大値を求めて
中央値と平均値を求めて、さらにそれぞれ平均を求める、という複雑な操作を加えた。これに伴う誤差については、まだ正確に評価はしていない。
16. 参考2:
下のグラフは、必要な時に数値が読み取り
やすいように、格子点を「+」マークにし
ました。こういう方法も広めたいです。
本資料に現れた N= 4, 10, 30, 111, 513 の数をそもそも、ど
うやって思いつくかについては、下記のような近似式を
使ってR言語による計算がひとつのヒントになる。
> log(2)/( pnorm ( seq(1,4,0.5) , lower.tail=F ) )
[1] 4.368889 10.375336 30.467831 111.623919
513.481140 2979.623972 21885.696311
> -qnorm(log(2)/c(4,10,30,111,513))
[1] 0.9412562 1.4809142 1.9934718 2.4980137 2.9997144
17. 18. Statement :
本資料で伝えたかった事を数学的に
表現すると、このスライド一枚のよ
うになります。
Assume Norm + ( m,s 2 ) be the distribution of the maximum value of
N
N stochastic variables distributed normally with mean m and variance s 2 .
Then for N = 4, 10, 30, each median value of Norm + (0,1) are,
N
approximately 0.9981, 1.4988, 1.9982, that are rounded down to
0.998, 1.498, 1.998, respectively. These are easy to remember as
1-e , 1.5-e , 2-e for N = 4, 10, 30 with e =0.002, thus possibly very useful
for your daily and social life. These numeric figures are calculated from
billions of Mersenne Twister psudo-ranom numbers using R language.
19.


![一様分布であれば話は簡単
[0,1]区間の一様分布から取り出し
たN個の乱数の最大値X(確率変数)
を考える。
Xの期待値(多数のXの平均値)は
N/N+1 と比較的容易な数式にな
る。
N
1
2
3
4
5
6
7
8
9
10
期待値 中央値 標準偏差
0.
500 0.
500
0.
289
0.
667 0.
707
0.
236
0.
750 0.
794
0.
194
0.
800 0.
841
0.
163
0.
833 0.
871
0.
141
0.
857 0.
891
0.
124
0.
875 0.
906
0.
110
0.
889 0.
917
0.
099
0.
900 0.
926
0.
090
0.
909
0.
933
0.
083
X の確率密度関数は N x N
N
X の期待値は
N 1
N
X の中央値は 1/ 2
1
N
X の標準偏差は
(N
2
1) ( N
2)
一様分布ではなく
て、ガウス分布だ
と、数式で求まるこ
とはないので、これ
から億単位の個数の
乱数から、実際に数
値計算をすることに
なる。](https://image.slidesharecdn.com/rr100b-131216044302-phpapp02/85/Rr100-b-4-320.jpg)
![予備知識 : ガウス分布とは
Histogram of runif(1e+06) + runif(1e+06)
60000
20000
Frequency
30000
0
0
10000
Frequency
50000
Histogram of runif(1e+06)
0.0
0.2
0.4
0.6
0.8
1.0
0.0
0.5
runif(1e+06)
1.0
1.5
2.0
runif(1e+06) + runif(1e+06)
120000
80000
Frequency
0
40000
100000
50000
0
Frequency
150000
Histogram of runif(1e+06) + runif(1e+06) + runif(1e+06)
Histogram of runif(1e+06) + runif(1e+06) + runif(1e+06) + runif(1e+06)
0.0
0.5
1.0
1.5
2.0
2.5
3.0
0
runif(1e+06) + runif(1e+06) + runif(1e+06)
1
2
3
4
runif(1e+06) + runif(1e+06) + runif(1e+06) + runif(1e+06)
80000
Histogram of rnorm(1e+06)
[0,1]区間から取り出した一様乱数を2回、3
回、4回と足し合わせたものをヒストグラ
ムにすると、その形は次第に、一定の形に
なる(ベルカーブ,左の図)。 その究極の形
の分布を、「ガウス分布」と呼ぶ。正規
分布とも呼ぶ。
2p s 2
4
ガウス分布は、多くの分布をよく近似す
る。たとえば、身長の分布、体重の分布、
測定誤差を伴う観測の結果の分布などを、
20000
40000
60000
e
平均値μを0、散らばりの尺度である標準
偏差σを1になるように調整したものを特
に、「標準ガウス分布」と呼ぶ。標準正
規分布とも呼ぶ。
0
Frequency
( x- m )2
2s 2
ガウス分布は数ある「分
布」の中で、とてもよく
知られている分布の一つ
です。
-4
-2
0
2](https://image.slidesharecdn.com/rr100b-131216044302-phpapp02/85/Rr100-b-6-320.jpg)
![予備知識 : 標準偏差 σ とは
60000
Frequency
40000
20000
0
○ 標準偏差 σ は、データの各値と平均
値の差を2乗したものの平均値に平方
根の操作を加えたものである。
80000
Histogram of rnorm(1e+06, 50, 10)
σは 「振れ幅」 に相当する尺度と考え
ると良い。
0
20
40
60
80
100
rnorm(1e+06, 50, 10)
ガウス分布から乱数 X を取り出した場合、
μ – σ < X < μ + σ となる確率は、68.27%
E
X
E X
2
各データの平均からのズレの2乗を「エネルギー」と考え、その
エネルギー量の期待値から求まる「ズレの相当量」を計算する
ため、平方根(2乗の逆変換)を取った、と考えると良いです。
E[ ・] は期待値です。
(平均値-2σ) は、偏差値30に相当する。
(平均値-σ) は、偏差値40に相当する。
平均値は、偏差値50に相当する。
(平均値+σ) は、偏差値60に相当する。
(平均値+2σ) は、偏差値70に相当する。
μ + σ < X となる確率は 15.87%
μ + 2 σ < X となる確率は、2.275%
μ + 3 σ < X となる確率は、0.135%
μ + 4.5 σ < X となる確率は、100万分の3.4
μ + 6 σ < X となる確率は、10億分の0.99
― 上記の値はR言語のpnorm関数で求まる。
多くの分布は、平均μ と標
準偏差 σ で特徴付けられ
るので、「σ」のこともよ
く理解しておくと、良い
です。](https://image.slidesharecdn.com/rr100b-131216044302-phpapp02/85/Rr100-b-7-320.jpg)
![結論
ここに現れる数値の組み合わせが、新発見でし
+1.00σ; 10回: +1.50σ ; 30回: た。
4回:
+2.00σ
"経験数"
N
算出に用いた
乱数の個数 M
最大値の中央値
[下2桁の標準誤差(SD )]
最大値の
期待値
1
―
0
0
4
10
30
41億
41億
51億
0.
998
1.
498
1.
998
147 [22]
802 [29]
224 [40]
各Nについて、M 個の乱数をN個ずつ
に分けて、それぞれの最大値を算出
する。それら(M÷N)個の数の中央値と
平均値が、それぞれ第3列と第4列で
ある。この2個の数は、0.03 程度の差
がある。
1. 93
02
1. 67
53
2. 27
04
やや日常的な解釈:
ガウス分布(μ,σは所与)か
ら、
30個の乱数を取り出す。
「その最大値はぴったり50%
の確率で、μ + 1.998.. σ 」以上
になる。同様に 「~」以下に
なる。
意味が分かれば、記憶しやすく、便利な数。
― 近似するとキリの良い数である。
― どの3個の値も、その近似値マイナス0.002 の操作で、さらに精度が
高まる。
各Nについて、50億個前後の擬似乱数を使いましたが、考えられる計算精度は、小数点
以下第4~5桁目に残っています。上記のような計算では、誤差の2乗に反比例して、乱
数の個数が必要となります。(1桁精度を上げるには、さらに100倍の個数の乱数が必要](https://image.slidesharecdn.com/rr100b-131216044302-phpapp02/85/Rr100-b-9-320.jpg)




![補足 :
今回は、R言語に実装されたプログラムが数値的に発
生させる「擬似乱数」を何百億個も使って計算しま
した。今回の計算は、誤差を小さくしようとする
と、その2乗に反比例して、多くの乱数を必要としま
す。擬似乱数ではなくて、物理乱数も使って計算し
て、比較検証もしたいです。
• R言語が生成する乱数は、メルセンヌツイスターを
使っているので、(おそらく)精度が良い(はず)。
• 今回は100億個超の乱数を発生させた。
• R言語による計算は、30分程度以下の作業の繰り返し。
• 中央値を求める median関数に時間がかかったようだ。
• 今回見つけた数は、たまたまキリが良かった。
ひょっとしたら、何か法則性があるかもしれな
い。
• [要考察] コルモゴロフ=スミルノフの検定を用いると、大抵の分布
は、数十個の点をサンプリングしても、ガウス分布となかなか区
別がつかない。考えようによっては、何か考えたいことをガウス
分布に近似させることは、十分に意味がある。](https://image.slidesharecdn.com/rr100b-131216044302-phpapp02/85/Rr100-b-14-320.jpg)
![参考1 : 本資料に用いた元の数表
"経験数"
N
最大値の中央値
[下2桁の標準誤差(SD )]
最大値の
期待値
1
―
0
0
4
10
30
110
111
510
511
512
513
514
515
•
算出に用いた
乱数の個数 M
41億
41億
51億
44億
44.
4億
122.
4億
174.
5億
102.
4億
513億
102.
8億
103億
0.
998 1 4 7
1.
498 8 0 2
1.
998 2 2 4
2.
495 892
2.
499 135
2.
998 102
2.
998 797
2.
999 237
2.
999 884
3.
000 461
3.
001 152
[2 7 ]
[3 5 ]
[4 6 ]
[79]
[84]
[86]
[63]
[96]
[43]
[97]
[99]
1.
02
1.
53
2.
04
2.
54
2.
54
3.
04
3.
04
3.
04
3.
04
3.
04
3.
04
93
67
27
15
47
27
27
27
44
50
56
“最大値の中央値” を 0.5刻みで変化させたときのNがどうなるかを考えようとして、たまたま発見した。
•
意味が解釈可能であって、たまたま、Nが2桁以下のときは全て、Nが記憶のしやすい数であった(4,10,30)。
•
そのときの中央値も小数点以下第3位で切り捨てると、 0.5の整数倍から 0.002 少ない数であった(0.998, 1.498, 1.998)。
•
•
ちょうど0.5の整数倍にはならないので、それに最も近い数を追求していたら、上記のような数表となった。
•
N=111, 511の場合は、小数点以下第3位で切り捨てると、 0.5の整数倍から 0.001 少ない数であった。
上記の表の誤差の可能性について
•
メモリの制約があったため、上記の数は、各Nについて、M個の乱数を、約1000万個ずつに分けて、さらにN個ずつに分けて最大値を求めて
中央値と平均値を求めて、さらにそれぞれ平均を求める、という複雑な操作を加えた。これに伴う誤差については、まだ正確に評価はしていない。](https://image.slidesharecdn.com/rr100b-131216044302-phpapp02/85/Rr100-b-15-320.jpg)
![参考2:
下のグラフは、必要な時に数値が読み取り
やすいように、格子点を「+」マークにし
ました。こういう方法も広めたいです。
本資料に現れた N= 4, 10, 30, 111, 513 の数をそもそも、ど
うやって思いつくかについては、下記のような近似式を
使ってR言語による計算がひとつのヒントになる。
> log(2)/( pnorm ( seq(1,4,0.5) , lower.tail=F ) )
[1] 4.368889 10.375336 30.467831 111.623919
513.481140 2979.623972 21885.696311
> -qnorm(log(2)/c(4,10,30,111,513))
[1] 0.9412562 1.4809142 1.9934718 2.4980137 2.9997144](https://image.slidesharecdn.com/rr100b-131216044302-phpapp02/85/Rr100-b-16-320.jpg)