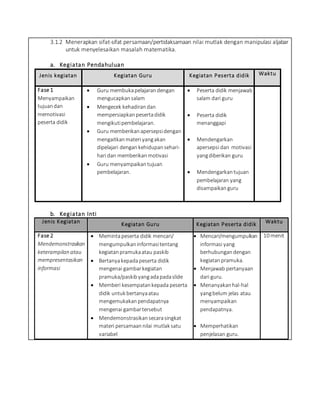
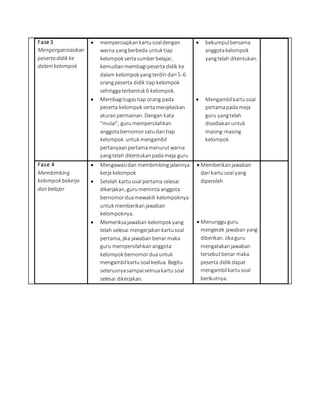
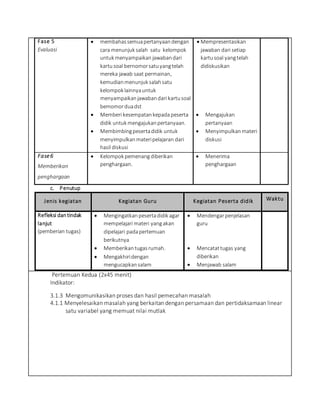
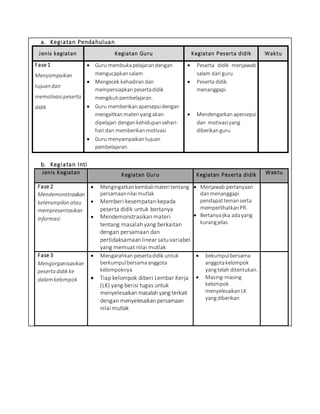
Dokumen ini adalah Rencana Pelaksanaan Pembelajaran (RPP) untuk mata pelajaran Matematika kelas X di SMAN 2 Makassar, berfokus pada pemahaman dan penerapan konsep nilai mutlak dalam persamaan dan pertidaksamaan. RPP ini mencakup kompetensi inti dan dasar, materi pembelajaran, metode pengajaran, serta evaluasi yang akan dilakukan. Pembelajaran dilakukan melalui pendekatan kooperatif dan berbagai kegiatan pembelajaran yang meliputi diskusi, demonstrasi, dan evaluasi kelompok.

1. RPP KD 3.1
RENCANA PELAKSANAAN PEMBELAJARAN (RPP)
Sekolah : SMAN 2 Makassar
Mata Pelajaran : Matematika
Kelas/Semester : X/1
Alokasi Waktu : 4 x 45 menit (2 pertemuan)
A. Kompetensi Inti (KI)
KI3: Memahami,menerapkan, menganalisis pengetahuan faktual, konseptual, prosedural berdasarkan
rasa ingintahunya tentang ilmu pengetahuan, teknologi, seni, budaya, dan humaniora dengan
wawasan kemanusiaan, kebangsaan, kenegaraan, dan peradaban terkait penyebab fenomena
dan kejadian, serta menerapkan pengetahuan prosedural pada bidang kajian yang spesifik sesuai
dengan bakat dan minatnya untuk memecahkan masalah
KI4: Mengolah, menalar, dan menyaji dalam ranah konkret dan ranah abstrak terkait dengan
pengembangan dari yang dipelajarinya di sekolah secara mandiri, dan mampu menggunakan
metoda sesuai kaidah keilmuan
A. Kompetensi Dasar (KD) dan Indikator
Kompetensi Dasar Indikator
KD pada KI 3
3.1 Mengintepretasi persamaan dan pertidaksamaan nilai mutlak dari
bentuk linear satu variabel dengan persamaan dan
pertidaksamaan linear Aljabar lainnya
KD pada KI4
4.1 Menyelesaikan masalah yang berkaitan dengan persamaan atau
pertidaksamaan nilai mutlak dari bentuk linear satu variabel
B. Materi Pembelajaran
1. Definisi nilai mutlak
2. Grafik nilai mutlak
3. Sifat-sifat nilai mutlak
4. Persamaan nilai mutlak
5. Menyelesikan persamaan nilai mutlak
6. Interval dan penyelesaian pertidaksamaan
7. Pertidaksamaan linear
8. Pertidaksamaan kuadrat dan penyelesaiannya
9. Menyelesaikan petidaksamaan nilai mutlak
C. Model dan Pendekatan/metode Pembelajaran : Kooperatif dengan strategi quick on the draw, tanya
jawab, penugasan dan diskusi
D. Kegiatan Pembelajaran
Pertemuan Pertama:
Indikator:
3.1.1 Mengenali kuantitas-kuantitas dan hubungan di antaranya dalam masalah yang memuatnilai
mutlak yang sesuai.

2. 3.1.2 Menerapkan sifat-sifat persamaan/pertidaksamaan nilai mutlak dengan manipulasi aljabar
untuk menyelesaikan masalah matematika.
a. Kegiatan Pendahuluan
Jenis kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Fase 1
Menyampaikan
tujuandan
memotivasi
peserta didik
 Guru membukapelajarandengan
mengucapkansalam
 Mengecek kehadirandan
mempersiapkan pesertadidik
mengikutipembelajaran.
 Guru memberikanapersepsidengan
mengaitkanmateri yangakan
dipelajari dengankehidupansehari-
hari dan memberikanmotivasi
 Guru menyampaikantujuan
pembelajaran.
 Peserta didik menjawab
salam dari guru
 Peserta didik
menanggapi
 Mendengarkan
apersepsi dan motivasi
yangdiberikan guru
 Mendengarkantujuan
pembelajaran yang
disampaikan guru
b. Kegiatan Inti
Jenis Kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Fase 2
Mendemonstrasikan
keterampilan atau
mempresentasikan
informasi
 Memintapeserta didik mencari/
mengumpulkaninformasitentang
kegiatanpramukaatau paskib
 Bertanyakepadapeserta didik
mengenai gambarkegiatan
pramuka/paskibyangadapadaslide
 Memberi kesempatankepada peserta
didik untuk bertanyaatau
mengemukakanpendapatnya
mengenai gambartersebut
 Mendemonstrasikansecarasingkat
materi persamaannilai mutlak satu
variabel
 Mencari/mengumpulkan
informasi yang
berhubungandengan
kegiatanpramuka.
 Menjawab pertanyaan
dari guru.
 Menanyakanhal-hal
yangbelum jelas atau
menyampaikan
pendapatnya.
 Memperhatikan
penjelasan guru.
10 menit

3. Fase 3
Mengorganisasikan
peserta didik ke
dalamkelompok
 mempersiapkankartusoaldengan
warna yangberbeda untuk tiap
kelompok sertasumberbelajar,
kemudianmembagipeserta didik ke
dalam kelompok yangterdiri dari 5-6
orangpeserta didik tiap kelompok
sehinggaterbentuk 6 kelompok.
 Membagitugastiap orang pada
peserta kelompok sertamenjelaskan
aturanpermainan. Dengan kata
“mulai”, gurumempersilahkan
anggotabernomorsatudari tiap
kelompok untuk mengambil
pertanyaanpertamamenurutwarna
yangtelah ditentukanpadameja guru
 bekumpulbersama
anggotakelompok
yangtelah ditentukan.
 Mengambilkartusoal
pertamapada meja
guru yangtelah
disediakanuntuk
masing-masing
kelompok
Fase 4
Membimbing
kelompok bekerja
dan belajar
 Mengawasidan membimbing jalannya
kerja kelompok
 Setelah kartusoal pertama selesai
dikerjakan, gurumeminta anggota
bernomorduamewakili kelompoknya
untuk memberikanjawaban
kelompoknya.
 Memeriksajawaban kelompok yang
telah selesai mengerjakankartusoal
pertama, jika jawaban benar maka
guru mempersilahkananggota
kelompok bernomorduauntuk
mengambilkartusoal kedua. Begitu
seterusnyasampaisemuakartu soal
selesai dikerjakan.
 Memberikanjawaban
dari kartusoal yang
diperoleh
 Menungguguru
mengecek jawaban yang
diberikan. Jikaguru
mengatakanjawaban
tersebutbenar maka
peserta didik dapat
mengambilkartusoal
berikutnya.

4. Fase 5
Evaluasi
 membahassemuapertanyaandengan
cara menunjuk salah satu kelompok
untuk menyampaikan jawabandari
kartusoal bernomorsatuyangtelah
mereka jawab saat permainan,
kemudianmenunjuk salahsatu
kelompok lainnyauntuk
menyampaikanjawabandari kartusoal
bemomorduadst
 Memberi kesempatankepada peserta
didik untuk mengajukanpertanyaan.
 Membimbingpesertadidik untuk
menyimpulkanmateripelajaran dari
hasil diskusi
 Mempresentasikan
jawaban dari setiap
kartusoal yangtelah
didiskusikan
 Mengajukan
pertanyaan
 Menyimpulkanmateri
diskusi
Fase6
Memberikan
penghargaan
 Kelompok pemenang diberikan
penghargaan.
 Menerima
penghargaan
c. Penutup
Jenis kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Refleksi dantindak
lanjut
(pemberian tugas)
 Mengingatkan pesertadidik agar
mempelajari materi yangakan
dipelajari padapertemuan
berikutnya
 Memberikantugasrumah.
 Mengakhiridengan
mengucapkansalam
 Mendengarpenjelasan
guru
 Mencatattugas yang
diberikan
 Menjawab salam
Pertemuan Kedua (2x45 menit)
Indikator:
3.1.3 Mengomunikasikan proses dan hasil pemecahan masalah
4.1.1 Menyelesaikan masalah yang berkaitan dengan persamaan dan pertidaksamaan linear
satu variabel yang memuat nilai mutlak

5. a. Kegiatan Pendahuluan
Jenis kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Fase 1
Menyampaikan
tujuan dan
memotivasipeserta
didik
 Guru membukapelajarandengan
mengucapkansalam
 Mengecek kehadirandan
mempersiapkan pesertadidik
mengikutipembelajaran.
 Guru memberikanapersepsidengan
mengaitkanmateri yangakan
dipelajari dengankehidupansehari-
hari dan memberikanmotivasi
 Guru menyampaikantujuan
pembelajaran.
 Peserta didik menjawab
salam dari guru
 Peserta didik
menanggapi
 Mendengarkan apersepsi
dan motivasiyang
diberikanguru
b. Kegiatan Inti
Jenis Kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Fase 2
Mendemonstrasikan
keterampilan atau
mempresentasikan
informasi
 Mengingatkankembalimateri tentang
persamaannilai mutlak
 Memberi kesempatan kepada
peserta didik untuk bertanya
 Mendemonstrasikan materi
tentang masalah yang berkaitan
dengan persamaan dan
pertidaksamaan linear satu variabel
yang memuat nilai mutlak
 Menjawab pertanyaan
danmenanggapi
pendapattemanserta
memperlihatkanPR.
 Bertanyajika adayang
kurangjelas.
Fase 3
Mengorganisasikan
peserta didik ke
dalamkelompok
 Mengarahkan pesertadidik untuk
berkumpulbersamaanggota
kelompoknya
 Tiap kelompok diberi Lembar Kerja
(LK) yang berisi tugas untuk
menyelesaikan masalah yang terkait
dengan menyelesaikan persamaan
nilai mutlak
 bekumpulbersama
anggotakelompok
yangtelah ditentukan.
 Masing-masing
kelompok
menyelesaikanLK
yangdiberikan

6. Fase 4
Membimbing
kelompok bekerja
dan belajar
 Guru sebagai fasilitator mengamati
kerja setiap kelompok secara
bergantian dan memberikan
bantuan secukupnya jika
diperlukan.
 Mengingatkan setiap peserta didik
supaya menerapkan keterampilan
kooperatif dalam kerja kelompok,
selalu menghargai pendapat orang
lain, dan memberikan kesempatan
kepada peserta didik lain untuk
menemukan idea kelompoknya
sendiri dan menjawab pertanyaan
peserta didik jika merupakan
pertanyaan kelompok.
 Peserta didik bekerja
samadengan anggota
kelompoknyadalam
mengerjakanLK
 Peserta didik bersama
anggotakelompoknya
mencari langkah
penyelesaiansoal yang
diberikan
Fase 5
Evaluasi
 Memberi kesempatankepada peserta
didik untuk mengajukanpertanyaan.
 Membimbingpesertadidik untuk
menyimpulkanmateripelajaran dari
hasil diskusi
 Guru mengkaji ulang proses pada
fase 1 sampai 4.
 Mengajukan
pertanyaan
 Menyimpulkanmateri
diskusi
Fase6
Memberikan
penghargaan
 Kelompok pemenangdiberikan
penghargaan.
 Menerima
penghargaan
c. Kegiatan Penutup
Jenis kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Refleksi dantindak
lanjut
(pemberian tugas)
 Dengan tanya jawab guru
mengarahkan semua peserta
didik pada kesimpulan
penyelesaiaan persamaan nilai
mutlak
 Guru memberikan beberapa soal
sebagai tugas / PR mengenai
penyelesaiaan persamaan nilai
mutlak Guru mengakhiri
kegiatan pembelajaran dengan
memberikan pesan untuk tetap
belajar dan mengucap salam
 Mendengarpenjelasan
guru
 Mencatattugas yang
diberikan
 Menjawab salam

7. Pertemuan Ketujuh-kesembilan:
Indikator:
4.1.2 Menyajikanpenyelesaianmasalahyang berkaitandenganpersamaandanpertidaksamaan
linear satu variabel yang memuat nilai mutlak
a. Kegiatan Pendahuluan
Jenis kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Fase 1
Menyampaikan
tujuan dan
memotivasipeserta
didik
 Guru membukapelajarandengan
mengucapkansalam
 Mengecek kehadirandan
mempersiapkan pesertadidik
mengikutipembelajaran.
 Guru memberikanapersepsidengan
mengaitkanmateri yangakan
dipelajari dengankehidupansehari-
hari dan memberikanmotivasi
 Guru menyampaikantujuan
pembelajaran.
 Peserta didik menjawab
salam dari guru
 Peserta didik
menanggapi
 Mendengarkan apersepsi
dan motivasiyang
diberikanguru
b. Kegiatan Inti
Jenis Kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Fase 2
Mendemonstrasikan
keterampilan atau
mempresentasikan
informasi
 Mengingatkankembalimateri tentang
menyelesaikanmasalah pertidaksamaan
nilaimutlak
 Memberi kesempatankepada peserta
didik untuk bertanya
 Menjawab pertanyaan
danmenanggapi
pendapattemanserta
memperlihatkanPR.
 Bertanyajika adayang
kurangjelas.
Fase 3
Mengorganisasikan
peserta didik ke
dalamkelompok
 Mengarahkan pesertadidik untuk
berkumpulbersamaanggota
kelompoknya
 Tiap kelompok diberi Lembar Kerja (LK)
yangberisi tugasuntuk menyelesaikan
masalahyangterkaitdengansistem
pertidaksamaannilaimutlak
 berkumpulbersama
anggotakelompok yang
telah ditentukan.
 Masing-masing
kelompok
menyelesaikanLK yang
diberikan

8. Fase 4
Membimbing
kelompok bekerja
dan belajar
 Guru sebagai fasilitator mengamati
kerja setiap kelompok secara
bergantiandan memberikanbantuan
secukupnyajikadiperlukan.
 Mengingatkansetiap peserta didik
supayamenerapkanketerampilan
kooperatifdalam kerja kelompok,
selalu menghargai pendapatorang
lain, danmemberikankesempatan
kepadapeserta didik lain untuk
menemukanidea kelompoknyasendiri
danmenjawab pertanyaan peserta
didik jika merupakanpertanyaan
kelompok.
 Peserta didik bekerja
samadengan anggota
kelompoknyadalam
mengerjakanLK
 Peserta didik bersama
anggotakelompoknya
mencari langkah
penyelesaiansoal yang
diberikan
Fase 5
Evaluasi
 Memberi kesempatankepada peserta
didik untuk mengajukanpertanyaan.
 Membimbingpesertadidik untuk
menyimpulkanmateripelajaran dari
hasil diskusi
 Guru mengkajiulang prosespada fase
1 sampai4.
 Mengajukan
pertanyaan
 Menyimpulkanmateri
diskusi
Fase6
Memberikan
penghargaan
 Kelompok pemenangdiberikan
penghargaan.
 Menerima
penghargaan
c. Kegiatan Penutup
Jenis kegiatan Kegiatan Guru Kegiatan Peserta didik Waktu
Refleksi dantindak
lanjut
(pemberian tugas)
 Dengan tanya jawab guru
mengarahkan semua peserta didik
pada kesimpulan mengenai sistem
persamaan dua variabel (linear-
kuadrat dan kuadrat-kuadrat)
 Guru memberikan beberapa soal
sebagai tugas / PR mengenai sistem
persamaan dua variabel (linear-
kuadrat dan kuadrat-kuadrat)
 Guru mengakhiri kegiatan
pembelajaran dengan memberikan
pesan untuk tetap belajar dan
mengucap salam
 Mendengarpenjelasan
guru
 Mencatattugas yang
diberikan
 Menjawab salam
E. Teknik penilaian
Tes Uraian
F. Media/alat, Bahan, dan Sumber Belajar
1. Media/alat : Notebook, Projector

9. 2. Bahan : Slide presentasi PPT, LKPD
3. Sumber Belajar : - Matematika SMA/MA/SMK/MAK Kelas X, Kemdikbud
- Matematika SMAkelas X Erlangga, Sartono Wirodikromo
Lampiran-lampiran:
1. Instrumen Penilaian Pertemuan 1
2. Instrumen Penilaian Pertemuan 2

10. Penilaian
Pengetahuan
a. Teknik Penilaian: Tes
b. Bentuk Instrumen: Uraian
Kisi-kisi Soal
IPK Materi Pembelajaran Indikator Soal Teknik Penilaian
Bentuk
soal
Nomor
soal
3.1.1 Mengidentifikasi
kuantitas-kuantitas dan
hubungan di antaranya
dalam masalah
kontekstual yang
memuat nilai mutlak
yang sesuai.
Persamaan dan
Pertidaksamaan Linear
Satu Variabel yang
Memuat Nilai Mutlak
Diberikan ilustrasi tentang jarak dan
perpindahan. Peserta didik dapat
Mengidentifikasi kuantitas-kuantitas dan
hubungan di antaranya dalam masalah
kontekstual
Tes tertulis uraian 1,2
3.1.2 Menerapkan konsep
matematika untuk
menyelesaikan
persamaan dan/atau
pertidaksamaan linear
satu variabel yang
memuat nilai mutlak.
Penerapan persamaan
dan pertidaksamaan
nilai mutlak
Diberikan soal persamaan/pertidaksamaan
yang menggunakan konsep matematika.
Peserta didik dapat menerapkan ide-ide
matematikauntuk menyelesaikan persamaan
dan/atau pertidaksamaan linear satu variabel
yang memuat nilai mutlak.
Tes tertulis uraian 3,4
4.1.1 Menerapkan sifat-sifat
pertidaksamaan nilai
mutlak dengan
manipulasi aljabar
untuk menyelesaikan
masalah matematika.
Sifat-sifat
pertidaksamaan nilai
mutlak
Diberikanbeberapasifat-sifatpertidaksamaan
untuk diterapkan pada soal latihan. Peserta
didik dapat menerapkan sifat-sifat
pertidaksamaan nilai mutlak dengan
manipulasi aljabar untuk menyelesaikan
masalah matematika.
Tes tertulis uraian 5
4.1.2 Menganalisis daerah
penyelesaian
pertidaksamaan nilai
mutlak
Menggambar daerah
penyelesaian
pertidaksamaan
Diberikan soal dan tabel kemudian
digambarkan dalam grafik. Peserta didik
dapat menganalisis daerah penyelesaian
pertidaksamaan nilai mutlak
Tes tertulis uraian 6

11. Petunjuk:
1. Berdoalah sebelum mengerjakan soal
2. Jawablah pada lembar jawaban yang telah disediakan
3. Selesaikan soal berikut dengan singkat dan jelas
Pedoman Penilaian Instrumen Pengetahuan Pertemuan I dan II
Soal Jawaban Skor
1. Pada suatu suatu kesempatan, firman mampu
berenang sejauh 10,8 m, sedangkan Abdullah
mampu berenang 5,9 m dari titik tolak. Berapa
selisih perpindahan anak tersebut?”
2. Pada mobil-mobil baru, angka kilometer per
liternya tergantung pada bagaimana mobil itu
digunakan, apakah sering digunakan untuk
perjalanan jarak jauh ataukah hanya untuk
perjalananjarak dekat(dalamkota). Untuk suatu
merek mobil tertentu, angka kilometer per
liternya berkisar di angka 2,8 kurang atau
lebihnyadari 12 km/L. Berapakahjangkauandari
angka km/L dari mobil tersebut?
1. |5,9 − 10,8| = |−4,9| = 4,9
2. Diketahui angka km/L dari suatu mobil berkisar di angka 2,8 kurang
atau lebihnya dari 12 km/L.
Misalkanm adalahangka km/Ldari mobil tersebut. Maka,selisih
m dan 12 tidak boleh lebih dari 2,8, atau dapat dituliskan ke
dalam |m – 12| ≤ 2,8.
Sehingga jangkauan dari angka km/L mobil tersebut adalah dari
angka 9,2 km/L sampai 14,8 km/L.
5
15

12. 3. Tentukan solusi dari
a. |2𝑥 + 1| = | 𝑥 − 2|
b. Jika f(x)= |4𝑥 − 7|, maka f(1) = …
3𝑎. |2𝑥 + 1| = | 𝑥 − 2|
↔ (2𝑥 + 1)2
= (𝑥 − 2)2
↔ (4𝑥2
+ 4𝑥 + 1) = (𝑥2
− 4𝑥 + 4)
↔ 3𝑥2
+ 8𝑥 − 3 = 0
↔ (𝑥 + 3)(3𝑥 − 1) = 0
↔ 𝑥 = −3 𝑎𝑡𝑎𝑢 𝑥 =
1
3
3b. f(x) = |4𝑥 − 7|
f(1) = |4(1) − 7|
= |−3| = 3
4. Tentukan nilai x dari pertidaksamaan
a. |5𝑥 + 3| > 8
b. |x + 5| < 3
4a. |5𝑥 + 3| > 8
5x + 3 < -8 atau 5x + 3 > 8
5x ≤ -11 atau 5x > 5
𝑥 < −
11
5
𝑎𝑡𝑎𝑢 𝑥 > 1
4b. |x + 5| < 3
↔ −3 < 𝑥 + 5 < 3
↔ −8 < 𝑥 < −2
𝐻𝑝: ↔ {−8 < 𝑥 < −2}
5. Tentukanlah penyelesaian dari pertidaksamaan
nilai mutlak |x – 2| ≤ |x + 1|
|x – 2| ≤ |x + 1|
↔ (𝑥 − 2)2
≤ (𝑥 + 1)2
↔ (𝑥2
− 4𝑥 + 4) ≤ (𝑥2
+ 2𝑥 + 1)
↔ −6𝑥 + 3 ≤ 0
↔ −6𝑥 − 3 ≤ 0
↔ 𝑥 ≤ 2

13. 𝑀𝑎𝑘𝑎 𝐻𝑝 = { 𝑥 ≤ 2}
6. Buatlah sketsa grafik f(x) = |x-3| 10
Total skor maksimal 100

14. LEMBAR PENGAMATAN PENILAIAN SIKAP
Mata Pelajaran : Matematika
Kelas/Semester : X/1
Tahun Pelajaran : 2016/2017
Waktu Pengamatan :
Indikator sikap aktif dalam pembelajaran nilai mutlak
1. Kurang baik jika menunjukkan sama sekali tidak ambil bagian dalam pembelajaran
2. Baik jika menunjukkansudahada usahaambilbagiandalam pembelajaran tetapibelumajeg/konsisten
3. Sangatbaik jika menunjukkansudahambilbagian dalam menyelesaikantugaskelompok secara terus
menerus dan ajeg/konsisten
Indikator sikap bekerjasama dalam kegiatan kelompok.
1. Kurang baik jika sama sekali tidak berusaha untuk bekerjasama dalam kegiatan kelompok.
2. Baik jika menunjukkan sudah ada usaha untuk bekerjasama dalam kegiatan kelompok tetapi masih
belum ajeg/konsisten.
3. Sangat baik jika menunjukkan adanya usaha bekerjasama dalam kegiatan kelompok secara terus
menerus dan ajeg/konsisten.
Indikator sikap toleran terhadap proses pemecahan masalah yang berbeda dan kreatif.
1. Kurangbaik jika samasekalitidak bersikaptoleranterhadapprosespemecahanmasalahyangberbeda
dan kreatif.
2. Baik jika menunjukkansudahadausahauntuk bersikaptoleran terhadapproses pemecahanmasalah
yang berbeda dan kreatif tetapi masuih belum ajeg/konsisten.
3. Sangat baik jika menunjukkansudah ada usaha untuk bersikap toleran terhadap proses pemecahan
masalah yang berbeda dan kreatif secara terus menerus dan ajeg/konsisten.

15. Bubuhkan tanda √pada kolom-kolom sesuai hasil pengamatan
No Nama
Sikap
Aktif Kerja Sama Toleransi
KB B SB KB B SB KB B SB
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Keterangan:
KB : Kurang baik
B : Baik
SB : Sangat baik

16. LEMBAR PENGAMATAN PENILAIAN KETERAMPILAN
Mata Pelajaran : Matematika
Kelas/Semester : X/1
Tahun Pelajaran : 2016/2017
Waktu Pengamatan :
Indikator terampil menerapkan konsep/prinsip dan strategi pemecahan masalah yang relevan yang
berkaitan dengan nilai mutlak
1. Kurang terampil jika sama sekali tidak dapat menerapkan konsep/prinsip dan strategi pemecahan
masalah yang relevan yang berkaitan dengan konsep nilai mutlak.
2. Terampil jika menunjukkan sudah ada usaha untuk menerapkan konsep/prinsip dan strategi
pemecahan masalah yang relevan yang berkaitan dengan konsep nilai mutlak
3. Sangat terampill, jika menunjukkan adanya usaha untuk menerapkan konsep/prinsip dan strategi
pemecahan masalah yang relevan yang berkaitan dengan konsep nilai mutlak
Bubuhkan tanda √pada kolom-kolom sesuai hasil pengamatan.
No Nama Siswa
Keterampilan
Menerapkan konsep/prinsip dan strategi
pemecahan masalah
KT T ST
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

17. No Nama Siswa
Keterampilan
Menerapkan konsep/prinsip dan strategi
pemecahan masalah
KT T ST
22
23
24
25
26
27
28
29
30
31
32
Keterangan :
KT : Kurang terampil
T : Terampil
ST : Sangat terampil
Kepala Sekolah
Makassar, 18 Juli 2016
Guru Mata Pelajaran
Dra. Hj. Masita, M.Si
NIP. 19620830 198411 2 001
Azlan Andaru, S.Pd